基于环路紧密度的复杂网络社区挖掘方法

刘大有，杨建宁，杨 博，赵学华，金 弟

（1.吉林大学 计算机科学与技术学院，长春 130012；2.吉林大学 符号与知识工程教育部重点实验室 长春 130012；3.天津大学 计算机科学与技术学院，天津 300072）

网络簇结构是复杂网络最普遍、最重要的拓扑结构属性之一，具有同簇结点相互连接密集，异簇结点相互连接稀疏的特点。复杂网络聚类方法旨在揭示出复杂网络中真实存在的网络簇结构［1］。目前已存在很多复杂网络社区挖掘算法，基本可分为三类：基于启发式的社区挖掘算法［2-7］，基于优化的社区挖掘算法［8-12］和基于概率生成模型的社区挖掘算法［13-16］。基于启发式的社区挖掘算法通常是给出社区挖掘的启发式信息，通过这些启发式知识来划分社区。如MFC算法［17］，HITS 算 法［2］，GN 算 法［3］及 多 种 变 种［4-5］以及WH算法［6］。基于优化的社区挖掘算法通常定义划分社区的目标函数，并优化目标函数使其达到最大值或接近目标函数的最大值进而得到社区的划分结果。如谱方法［8-9］，图分割 KL算法［10］，FN 算法［11］以及 GA 算法［12］。基于概率生成模型的方法通过建立网络生成模型，并根据极大似然原理生成模型中的参数，从而得到网络的社区划分。典型代表是基于随机块模型（stochastic block model）的方法［14-15，18-19］。

如何合理地确定社区个数是很多复杂网络社区挖掘方法面临的难题。如何设计出能客观评价社区结构优劣的目标函数是现有方法特别是基于优化的方法所面临的另一个主要问题。Newman等人［20］提出网络模块度Q函数是最广泛采用的一种优化目标，但研究发现Q函数存在分辨率极限等问题［21］。

2004年Radicchi等人［4］提出了连接聚类系数，认为簇间边应很少出现在短回路中，否则短回路中其他多数连接也可能成为簇间连接，从而显著增加簇间连接密度。文献［4］将连接聚类系数定义为包含该链接的短回路数目，并认为簇间连接的连接聚类系数应小于簇内连接，在算法每次迭代中删除网络中连接系数最小的连接，直到划分出合理的社区。但算法时间复杂度较高。

本文属于基于启发式的社区挖掘算法，所用启发性知识与文献［4］相同，但提出了更为有效的短回路搜索策略和基于该策略的社区挖掘方法，并通过实验对环路与社区之间的联系做了更为细致的分析。

1 环路紧密度算法（LTA）

1.1 算法基本思想

通过一次遍历图中所有的边（假设研究的是无权无向图），若i结点到j结点有两条完全不重合的路径，则说明i，j同属于一个环路。若环路上结点的个数p小于某个特定的值α，则认为此环路紧密。认为紧密环路内结点仅包含于一个社区，否则环路内大部分边会成为社区间连接，这样会大大增加社区间的连接密度［4］。且认为不在同一社区中的结点，即使结点之间存在两条完全不重合的路径，但这样的两条路径所构成的环路一般周长较长，即此环路一般是疏松的。通过合理设计算法，可通过一次遍历网络得到网络中所有的紧密环路。表1为算法描述中使用的符号和定义。

表1 算法描述中用到的符号及说明Table 1 Symbols and description used in algorithm

步骤一：利用广度优先遍历算法遍历全图。在当前访问结点集合中选取要访问的结点。若结点之前未被访问，则将其前向结点记录，并将该结点的邻居结点（不包含其前向结点）加入下次访问结点集合，转步骤四；若结点已被访问，则必存在至少两条不同的路径能访问到当前结点，故存在环路，转步骤二。

步骤二：找出遍历到当前结点的两条不同的路径，得到环路。判断环路结点个数p是否满足条件p≤α，若满足则环路足够紧密，转步骤三；若不满足条件，转步骤四。

步骤三：若在所有环路中有两个紧密环路有边重合，则将两个环路合并，将两个环路合并后称为一个核，若是当前找到的紧密环路与某个核有边重合，则将该环路合并到核内，若在合并过程中引起某核与核之间有边重合，同样进行合并。以此类推，得到最终的核；若该紧密环路不与任何环路或是核有边重合，则做为独立的核存在。

步骤四：若当前访问结点集合不空，在当前访问结点集合中选取一个结点做为下一次访问的结点，转步骤一；若当前访问结点集合为空，转步骤五。

步骤五：若待访问结点集合为空，算法结束。转步骤六。

步骤六：最后将不在任何核中的结点通过计算其与各个核的紧密程度，取与各个核中最为紧密的的核作为其社区归属。

算法只需一次遍历整个图，便可以得到图中的所有最小环路，通过合并环路与环路、环路与核、核与核，最终得到核的个数作为社区的个数。

1.2 基本的LTA算法

S表示结点结合，Sg表示从S0开始算起，第g代待访问结点的集合，即从种子结点，遍历g步得到的结点集合，∀i，Si∈S。从V中选取种子结点seed，把seed加入到S0中。算法的伪代码如算法1（应用于非加权网络）所示。

算法1：

1.3 扩展的LTA算法

LTA算法对α值较敏感，若要得到真实的社区划分，需设定恰当的α值。把算法扩展到有权无向图中，使算法的应用范围更广。

扩展后算法的主要目的是寻找在加权网络中的紧密环路以及各个社区的核结点。其中计算环路紧密性包括两方面：

式（1）与式（2）分别表示加权图环路紧密值和环路周长。对Cfk，pk限制条件亦改为两方面：

特别地，当图中边的权重都为1（无权无向图）时，Cfk＝pk。

根据以上内容对LTA算法进行扩展，如算法2（应用于加权网络）所示。

算法2：

此修改使得LTA不能找到所有环路，为找到所有环路，可采用多次LTA，对每次LTA得到的结果进行合并，亦可达到很好的效果。例如洪泛得到的两个核集分别用X，Y 表示。X中含有个 核，Y 中 含 有个 核。则 对 （∀i，∀j）combine（Xi，Yj）。用cooccuri，j来表示核Xi和核Yj之间共现的结点数，若或则执行合并Xi和Yj。若Xi和Yj未能执行合并操作，则将Xi∩Yj中结点社区归属均置为空，在1.1节步骤六中作为未被加入到核结构的结点做算法后处理。

1.4 算法后处理

通过LTA算法计算得到C，将C中每个核作为一个社区，而C并不包含图G中所有的结点，会有一些结点本身就不在环路中（如该结点的度为1），此时要对LTA算法运行的结果进行后处理。处理办法是计算各社区中包含该结点邻居数最多的社区，并将其作为其本身的社区归属，见算法3（LTA的后处理算法）。

算法3：

1.5 算法效率分析

算法利用宽度优先遍历策略遍历图中每一条边，故时间复杂度为O（m）；算法在检测到某结点存在于环路中时，计算环路周长以及Cf值的时间复杂度为O（αnlog（n））；故总体上算法的时间复杂度为：O（m＋αnlog（n）），对于稀疏网络为：O（αnlog（n））。

2 实验与评估

论文中实验设备为个人PC，中央处理器为Intel（R）Core（TM）2Duo CPU E8400 ＠3.00GHz 2.99GHz，内存为 4.00GB（3.46GB usable），操作系统为 Windows 732b。所用编程语言是Matlab。

2.1 人工合成网络

为了评估算法的有效性，论文利用文献［22］提出的Lancichinetti model基准数据模型作为数据生成器，该模型提供了丰富的网络属性参数设置，包括最大度，平均度，度分布，网络社区最大规模，网络社区最小规模，网络社区重叠比例，结点个数，网络社区多重度分布和网络社区多重规模分布的设置。论文采用normalized mutual information（NMI）对算法挖掘社区的精度进行评估。

采用Lancichinetti model共生成3组数据，皆为无权无向图。第1组数据用来分析环路结点个数阈值α对社区挖掘效果的影响。第2组数据用来测试算法挖掘网络社区的精度。第3组数据用来测试算法挖掘网络的效率。

（1）第1组网络数据。设置结点个数n为128，社区最小规模Cmin为10（网络社区规模指其中包含的网络结点数目），网络最大规模Cmax为50，网络结点最大度dmax为20，网络结点平均度davg设置为4到13，社区间重叠结点比例μ设置为0.05。网络结点度分布指数τ1设置为－1，网络社区规模分布指数τ2设置为－1。共10小组不同的设置，且根据每小组的数据设置，重复生成10个网络，共100个网络。

（2）第2组网络数据。设置n为128，Cmin为50，Cmax为70，dmax为20，davg为15，τ1为－1，τ2为－1，μ为从0.05到0.5共10小组不同的设置。特别地，当μ设置为0时，表示社区间没有边连接，相当于各个社区是独立的连通子图，其挖掘精准度应为1。且根据每小组的数据设置重复生成10个网络，共100个网络。

③第3组网络数据。n为从500到5000，Cmin为20，Cmax为100，dmax为20，davg设为15，τ1为－1，τ2为－1，μ为0.05，共10小组不同的数据。特别地，当n设置为0时，表示网络没有结点，则算法运行时间应为0s。

LTA算法中主要的参数为α和β，鉴于Lancichinetti model未提供生成加权人工数据的功能，实验只对α做分析。试验中，α分别取3到9共7个值。基准网络平均度davg为4到13，随着davg的增加，网络稠密度增加，则理论上社区间连接更加紧密，若要正确挖掘网络中的社区，则对α值的要求应愈加严格。如图1所示。算法在davg分别取4，5和α取3到6时，算法挖掘社区的精度均能达到90%以上，随着davg的增大，网络稠密度增加，社区挖掘的高精度对α的要求越来越苛刻。所幸的是，在图1中可以看到当α＝3时，能从容面对davg在所有取值下的人工网络。此结论也从另一方面说明同处于α＝3的紧密环路的结点在很大程度上处于同一网络社区。

图1 不同α取值情况下的NMI变化情况Fig.1 NMI variations in terms ofα

图2 不同网络对应的NMI变化情况Fig.2 NMI variations in terms of different networks

利用第2组数据进行实验得到的结果如图2所示。图2中y轴表示每小组网络执行LTA结果的NMI精度值，x轴表示每小组网络对应的μ值。图中红色曲线表示10组网络执行结果NMI精度平均值曲线。从图2中可知，当μ为0、0.05和0.1时算法挖掘精度接近为1，随着μ值的增大，网络社区结构越来越不明显，挖掘精度也随之下降。算法较适合社区间连接稀疏的网络。

为了更好地对算法的执行效率进行分析，现对结点数目从500到5000的网络逐一测试，所得结果如图3所示。

图3 LTA算法运行时间图Fig.3 Running time of the LTA

2.2 真实基准网络数据集

为了进一步验证算法的可行性，算法使用无权无向图Dolphin网络［23］对LTA进行实验。另采用Karate加权无向网络［24］对扩展LTA进行实验。

2.2.1 Dolphin网络

图4中所示的红色结点和蓝色结点分别表示LTA算法找到的两个核，白色结点表示未加入核的结点。分析发现结点dn63在环内，但未被加入到核中，这是因为其处于两社区边缘区域，如前文分析，这种情况的出现对社区的划分有促进作用，更有助于准确进行社区挖掘。对图4中填充色为白色的结点进行后处理，依据算法GetGroup对图4中结果后处理所得结果如图5所示。此实验结果完全符合Dolphin网络的实际社区划分情况。

图4 Dolphin网络的核结构图Fig.4 The cores structure of the Dolphin network

图5 Dolphin网络的社区结构图Fig.5 The communities structure of the Dolphin network

2.2.2 Karate网络

为了验证LTA对加权图扩展算法的可行性，用加权Karate网络作为测试数据。实验前的邻接矩阵和结构图分别如图6和图7所示，其中图6中X轴和Y轴表示对应结点的编号，蓝色点表示对应结点之间的边。

执行算法LTA，得到网络核结构对应的邻接矩阵和结构图分别如图8和图9所示。图8中红色（蓝色）正方形内中的蓝色点表示得到的一个核结构所包含的边集，称为红色（蓝色）核。图9所示为所得两个核的结构图，其中未加入核的结点未在图中绘出。

依据算法GetGroup进行后处理所得结果的邻接矩阵和结构图分别如图10和图11所示。图10中红色（蓝色）正方形中所含边集对应图8，图9中的红色（蓝色）核。图11表示对应的红色社区与蓝色社区结构图。所得结果与真实社区划分完全相同。

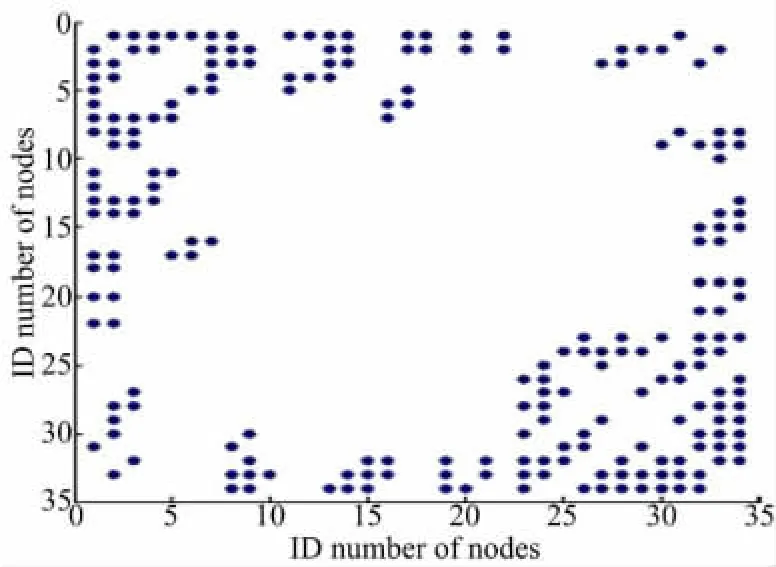
图6 Karate网络的邻接矩阵图Fig.6 The adjacency matrix of Karate network

对于Karate网络，其结构图利用Netdraw工具画出，且此工具包含对图的faction分析。其中faction分析包含两种模式：Quality模式和Speed模式。利用faction分析中的Quality模式分析得到的图与论文中LTA算法实验得到的结果完全相同。而在Speed模式下，结点16被分到图中的红色社区。仔细研究结点16发现，其处于社区的边缘，故将其划分到任一社区皆可，其效果如图12所示。

图7 Karate网络的结构图Fig.7 The structure of the Karate club network

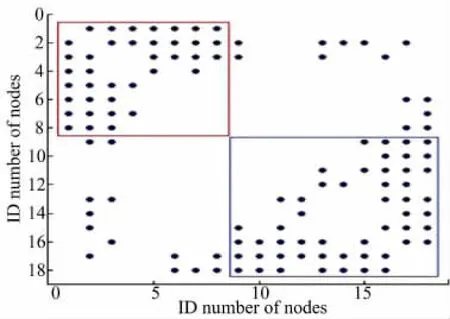
图8 Karate网络的核邻接矩阵图Fig.8 The adjacency matrix of the cores of Karate

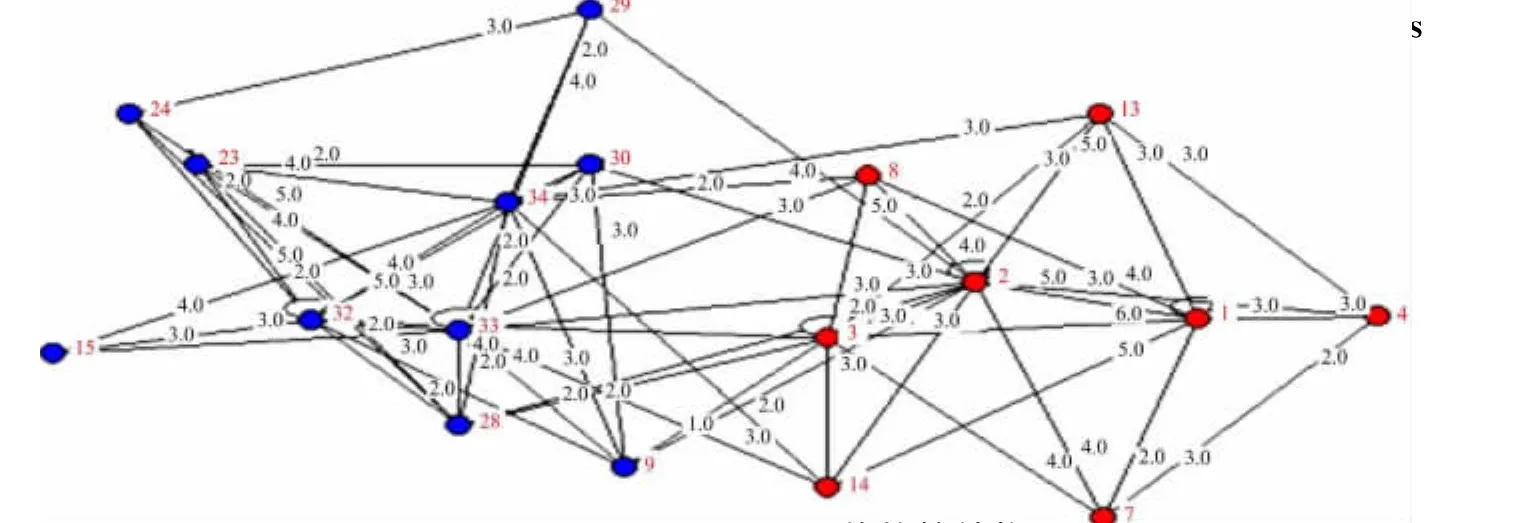
图9 Karate网络的核结构图Fig.9 The cores structure of the Karate club network

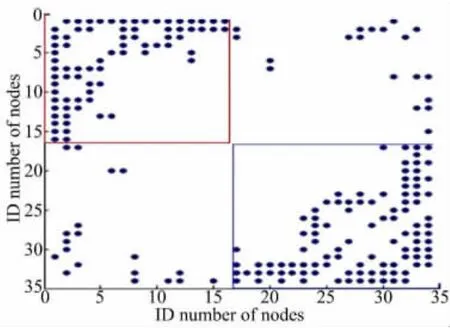
图10 Karate网络的社区邻接矩阵图Fig.10 The adjacency matrix of Karate network

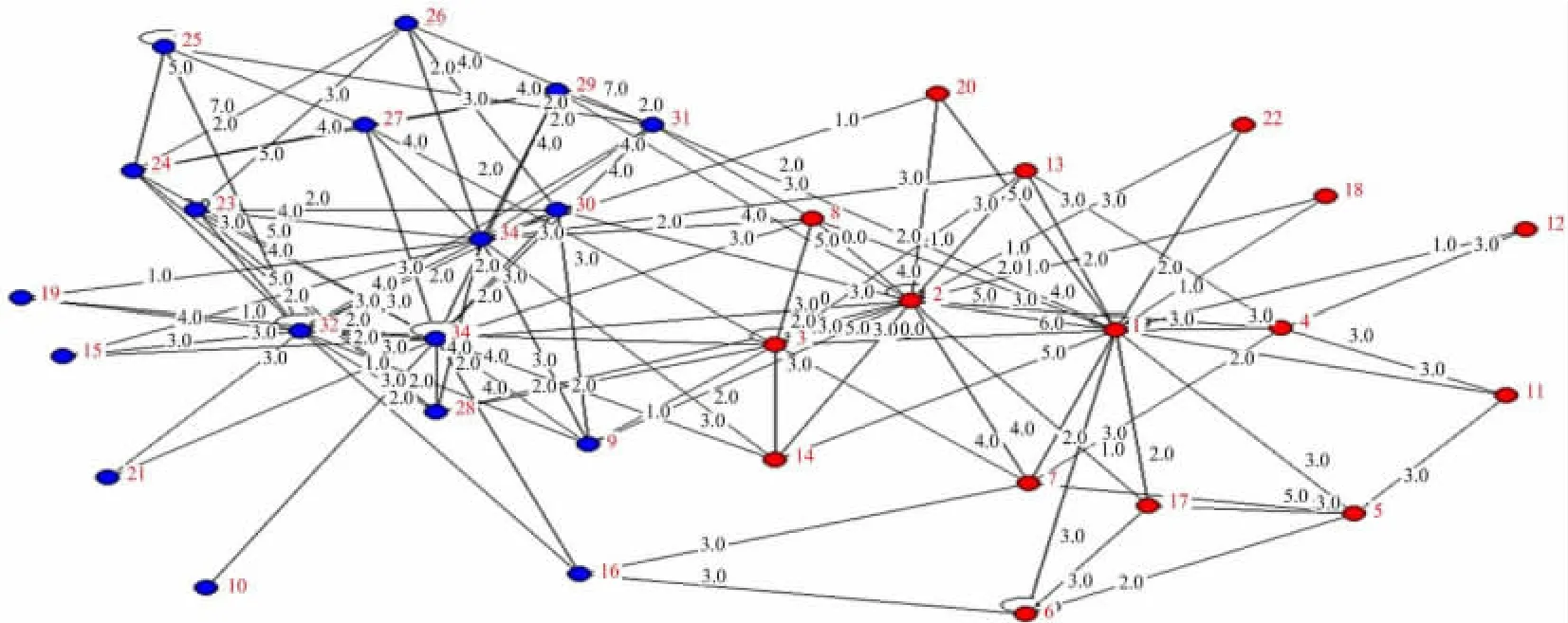
图11 Karate网络的核结构图Fig.11 The communities structure of the Karate club network

图12 利用Netdraw工具对Karate网络的分析结果Fig.12 The results of using Netdraw to analyze the Karate club network

3 结束语

针对社区挖掘问题，研究了网络中环路紧密度与社区结构的关系，进而提出了基于环路紧密度的社区挖掘算法LTA。LTA算法的一个主要优点是不需事先指定社区个数K。实验结果表明：LTA算法挖掘精度较高，且算法稳定性较好；同时，还验证了处于同一紧密环路中的两个结点处于同一社区的概率较大，处于不同社区的两个结点处于不同环路的概率较大这一思想；此外发现当LTA算法将参数α设置为3时，处于同一紧密环路中的结点会以极大概率出现在同一社区中。

［1］杨博，刘大有，Liu Ji－ming，等.复杂网络聚类方法［J］.软件学报，2009，20（1）：54－66.Yang Bo，Liu Da－you，Liu Ji－ming，et al.Complex network clustering algorithms［J］.Journal of Software，2009，20（1）：54－66.

［2］Kleinberg J M.Authoritative sources in a hyperlinked environment［J］.Journal of the ACM （JACM），1999，46：604－632.

［3］Girvan M，Newman M E J.Community structure in social and biological networks［J］.Proceedings of the National Academy of Sciences，2002，99：7821.

［4］Radicchi F，Castellano C，Cecconi F，et al.Defining and identifying communities in networks［J］.Proceedings of the National Academy of Sciences of the United States of America，2004，101：2658.

［5］Tyler J R，Wilkinson D M，Huberman B A.Email as spectroscopy：Automated discovery of community structure within organizations［J］.The Information Society，2005，21（2）：143－153.

［6］Wu F，Huberman B A.Finding communities in linear time：aphysics approach［J］.The European Physical Journal B－Condensed Matter and Complex Systems，2004，38：331－338.

［7］Yang B，Cheung W K，Liu J.Community mining from signed social networks［J］.IEEE Transactions on.Knowledge and Data Engineering，2007，19：1333－1348.

［8］Pothen A，Simon H D，Liou K P.Partitioning sparse matrices with eigenvectors of graphs［J］.Siam J Matrix Anal Applic，1990，11：430－452.

［9］Fiedler M.Algebraic connectivity of graphs［J］.Czech－oslovak Mathematical Journal，1973，23：298－305.

［10］Kernighan B W，Lin S.An efficient heuristic procedure for partitioning graphs［J］.Bell System Technical Journal，1970，49：291－307.

［11］Newman MEJ.Fast algorithm for detecting community structure in networks［J］.Physical Review E，2004，69：066133.

［12］Guimera R，Amaral L A N.Functional cartography of complex metabolic networks［J］.Nature 2005，433：895－900.

［13］Xing E P，Jordan M I，Russell S.A Generalized Mean Field Algorithm for Variational Inference in Exponential Families.Uncertinty in AI 2003.

［14］Fu W，Song L，Xing E P.Dynamic mixed membership blockmodel for evolving networks［C］∥In Proceedings of the 26th Annual International Conference on Machine learning，2009：329－336.

［15］Airoldi E M，Blei D M，Fienberg S E，et al.Mixed membership stochastic blockmodels［J］.The Journal of Machine Learning Research，2008，9：1981－2014.

［16］Wang Y J，Wong G Y.Stochastic blockmodels for directed graphs［J］.Journal of the American Statistical Association，1987：8－19.

［17］Flake G W，Lawrence S，Giles C L，et al.Self－organization and identification of web communities［J］.Computer，2002；35：66－70.

［18］Hofman J M，Wiggins C H.Bayesian approach to network modularity［J］.Physical Review Letters，2008，100：258701.

［19］Holland P W，Leinhardt S.Local structure in social networks［J］.Sociological methodology 1976，7：1－45.

［20］Newman M E J，Girvan M.Finding and evaluating community structure in networks［J］.Physical Review E，2004，69（2）：026113.

［21］Guimera R，Sales－Pardo M，Amaral L A N.Modularity from fluctuations in random graphs and complex networks［J］.Physical Review E，2004，70：025101.

［22］Lancichinetti A，Fortunato S.Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities［J］.Physical Review E，2009，80：016118.

［23］Lusseau D，Schneider K，Boisseau O J，et al.The bottlenose dolphin community of doubtful sound features a large proportion of long－lasting associations［J］.Behavioral Ecology and Sociobiology，2003，54：396－405.

［24］Zachary W W.An information flow model for conflict and fission in small groups［J］.Journal of Anthropological Research，1977：452－473.