液力变矩器导轮空转特性无叶片数值仿真

刘树成，魏 巍，闫清东，周 洽

（北京理工大学 机械与车辆学院，北京 100081）

液力变矩器是车辆液力传动系统的重要部件。对于综合式液力变矩器，在进入牵引工况下的偶合器工况后，其导轮处于空转状态，除了牵引工况，变矩器也可能出现涡轮转矩改变方向的反传工况，这时导轮也处于空转状态。近年来，对于变矩器全外特性的研究逐渐展开，其中导轮空转特性的研究是重要一环。然而，变矩器反传工况比常用的牵引工况要恶劣，对变矩器性能试验台的要求较高，在常规试验条件下对变矩器反传工况的研究只能局限在较窄的速比范围内，而且导轮空转转速不易直接测量，因此借助于仿真手段研究导轮空转特性就成为当然选择。

近年来变矩器流场数值模拟技术发展迅速，吉林大学［1-2］、北京理工大学［3］、上海交通大学［4］等高校的研究人员做了大量研究，仿真结果与试验数据吻合很好，实践证明变矩器流场数值模拟技术已经成为变矩器性能研究及预测的有力工具，但上述文献对于变矩器导轮（或者多工作轮液力元件的空转轮）空转特性的研究，一直采用传统的零转矩试算法（简称试算法）［5-6］进行仿真，即设定初值—计算—修改初值—计算……，多次反复直到导轮转矩接近于零。试算法以计算结果中的导轮转矩等于零为计算目标，反复修改导轮转速并计算，不仅可以获得导轮空转的变矩器转矩特性，而且可以得到导轮空转转速值，但流体网格数目较多或者瞬态求解时，每次试算耗时很长，多次反复试算工作冗繁，不能快速获得相应工况下的变矩器传动特性。

本文首先分析了导轮在变矩器工作液体循环中的导流作用，在此基础上提出一种不依赖于导轮空转转速的仿真方法——无叶片法，采用该方法和传统的零转矩试算法对变矩器导轮空转特性进行了仿真。

1 基本计算方程

液力变矩器内部流动可按黏性不可压流体的湍流运动处理，工程上常采用Reynolds平均法（RANS）来计算这种湍流运动，在Reynolds应力项的处理上，多数CFD软件常采用Boussinesq提出的涡黏假定，把Reynolds应力表示成湍动黏度的函数，那么计算湍流流动的关键就是确定湍动黏度。本文采用工程上处理黏性不可压流动最常用的两方程模型标准k－ε模型［7］来处理湍动黏度。在稳态工况下，忽略浮力项，其输运方程［8］可以表示为

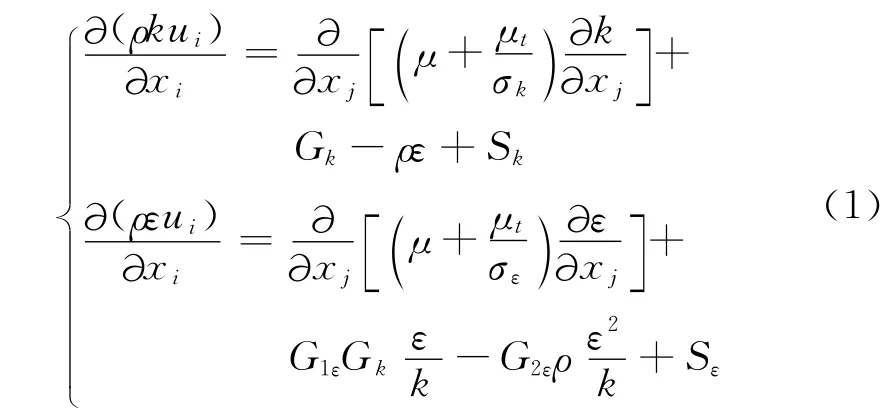
式中：Gk是由于平均速度梯度引起的湍动能k的产生项；G1ε、G2ε为经验常数；σk、σε分别是与湍动能k和耗散率ε对应的Prandtl数；Sk和Sε是用户定义的源项。

不考虑换热问题，其控制方程组只由连续性方程和动量方程组成，可表示为［9］

式中：φ为广义变量，对于连续性方程φ＝1，对于动量方程φ ＝ ｛u，v，w｝T；Γ 为扩散系数，对于连续方程Γ＝0，对于动量方程Γ＝μ＋μt，μ为动力黏度，μt为湍动黏度；u为速度向量；S为广义源项；ρ为工作液体密度；▽为哈密顿算子。

2 导轮导流作用分析

在液力变矩器中，由于导轮的存在，涡轮输出力矩与泵轮和导轮力矩之和平衡。在导轮固定时，导轮力矩与泵轮力矩同向，使得涡轮力矩大于泵轮力矩，从而实现变矩作用。导轮对液流的导向作用，可以从轴面（变矩器回转轴所在的平面）和流面（与流线平行的截面）两个方向来分析。

在轴面内，导轮与泵轮、涡轮的内、外环一起将工作液体限定在循环圆内，由于导轮内、外环的导流作用，从涡轮流出的液流得以完成循环圆方向的流动返回泵轮工作腔，进入下一个循环，如图1所示（图中虚线代表液流流线，下同）。无论导轮是空转还是固定，导轮内、外环的这种导向作用始终存在。

图1 导轮在轴面内的导流作用Fig.1 Stator’s flow-guiding effect on axial plane

在流面内，由于导轮叶片的存在，若导轮固定，流线基本与叶片骨线平行，如图2所示；若导轮空转，其空转阻力矩可近似为零，导轮叶片对液流的导向作用甚微，液流可以认为是按照进入导轮时的初始方向流动，最终进入泵轮工作腔。

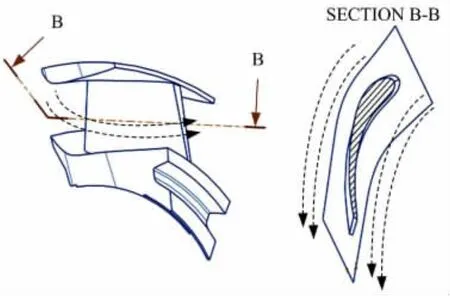
图2 导轮在流面内的导流作用Fig.2 Stator’s flow-guiding effect on stream surface

除此之外，导轮叶片和内外环壁面对工作液体还有冲击和摩擦作用，这种作用只有在导轮固定时才会变得显著，而在导轮空转时，这种作用在圆周方向的效果微乎其微，这主要是由于导轮在液流作用下可以自由转动的缘故，而在轴面循环圆方向上导轮内外环壁面对流体仍有一定的冲击和摩擦作用。

3 无叶片仿真法

基于导轮导流作用分析，当导轮空转时，导轮叶片对于液流的导向作用可以忽略，只存在内外环面对液流的导向作用。因此可以将导轮叶片去掉，并且将去掉叶片的导轮流体模型固定，建立其仿真模型如图3所示。

图3 无叶片变矩器内流体仿真模型Fig.3 Fluid modal used in bladeless method

图4所示的是传统试算法模型，图3和图4所示仿真模型均是按照各工作轮叶片数目，各取一个循环单元的流道模型，最后按照循环对称边界扩展到整个工作轮。采用混合平面法［10］进行仿真，湍流模型选用标准k－ε模型。在壁面条件设置上，泵轮和涡轮叶片及内、外环按照无滑移边界（No slip wall）处理，忽略导轮内、外环壁面对液流在循环圆方向的冲击和摩擦作用，将导轮内、外环设定为自由滑移边界（Free slip wall），而传统试算法模型中包括导轮内、外环在内的所有固体壁面均设为无滑移边界。

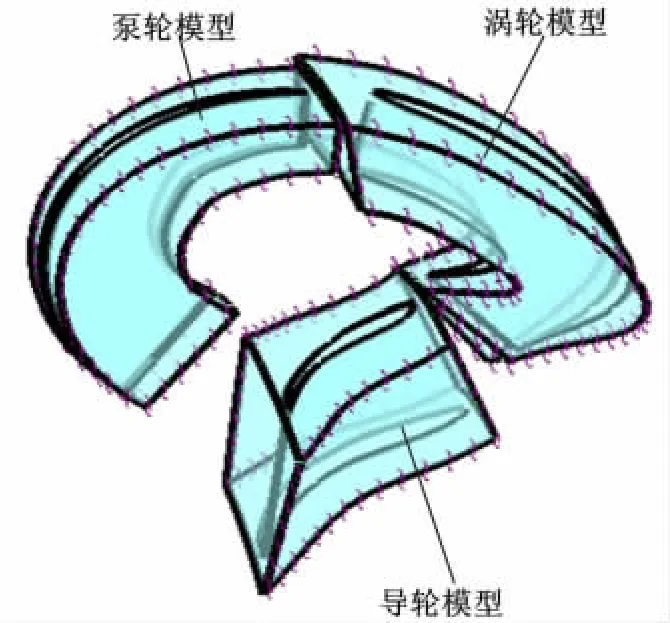
图4 传统试算法模型Fig.4 Fluid modal used in traditional method

无论是传统试算法还是无叶片法，都需要在泵轮、涡轮和导轮求解域之间设定交界面，由于无叶片法泵轮和涡轮求解域与传统试算法完全相同，只有导轮去掉了叶片，其求解域内部才会出现差异，但在涡轮－导轮、导轮－涡轮求解域交界面上仍保持流量守恒。

4 仿真结果分析

本文研究对象为某三元件综合式液力变矩器，有效直径为430mm，采用的工作油密度为835kg／m3，动力黏度为0.0102Pa·s。在泵轮恒定转速（2000r／min）下，涡轮转速按照转速比设定，对于无叶片法，导轮转速设定为0，对于试算法，导轮转速需要多次设定试算，直到导轮转矩为零。所研究变矩器在转速比为0.85左右开始进入偶合器工况，导轮开始空转。

基于近似相等的网格数量，应用图3和图4所示的仿真模型，分别采用无叶片法、传统试算法两种仿真方法对转速比为0.85～1.7的各个导轮空转工况点进行了仿真，其变矩比的仿真结果如图5所示。

图5中给出了转速比从0到1.0的试验数据以及试算法仿真结果，结果显示传统的试算法模型具有较高的仿真精度。在转速比为1.0以后（限于试验条件，未能给出试验值），可以看到无叶片法和试算法的仿真结果吻合很好，二者计算误差小于3%。

图6给出了传统的试算法和无叶片法两种仿真方法计算出的泵轮和涡轮转矩计算结果的对比情况。从中可以看出用无叶片法和传统的试算法得到的变矩器泵轮和涡轮转矩值走势一致，用无叶片法得到的泵轮和涡轮转矩值（绝对值）稍大于试算法的数值，二者计算误差小于10%。

图5 变矩比K值的仿真与试验结果Fig.5 Moment ratio results of simulation and experiment

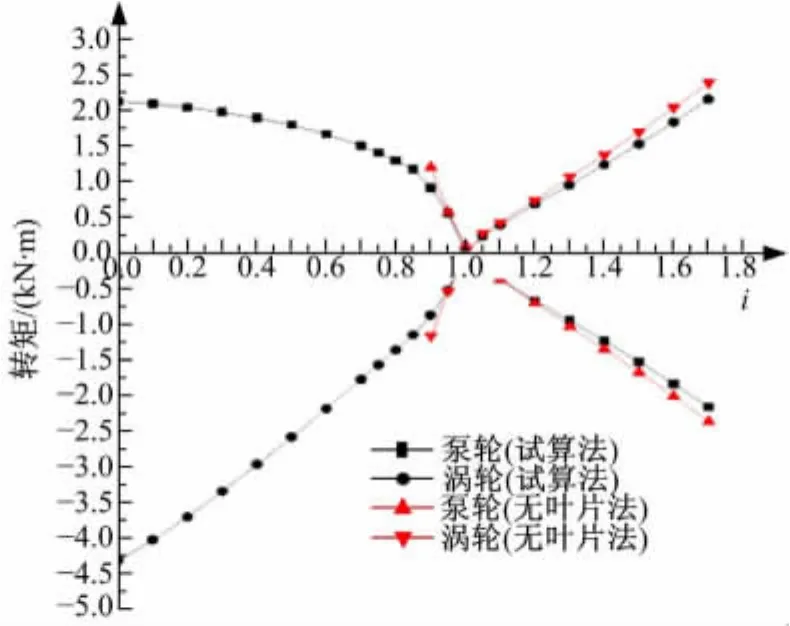
图6 用两种方法计算出的泵轮和涡轮转矩值Fig.6 Moment value of pump and turbine wheel obtained by two methods

图7给出了用试算法和无叶片法计算得到的循环流量对比结果，从中可以看出两种方法计算出的循环流量基本一致，但无叶片法计算得到的数值（绝对值）较试算法的结果稍小，二者误差小于10%，这种差别正是由于无叶片法忽略了导轮叶片，使得导轮工作腔的计算容积增大，液流在流经导轮时的循环流动中的流量容积损失增大，对循环流量起到一定的减弱作用。

由无叶片法计算出的循环流量（绝对值）稍小于零转矩试算法，而转矩值却稍大，这种现象可由束流理论做出解释。以涡轮转矩为例（这时涡轮转矩和泵轮转矩基本相等），其计算公式［11］为

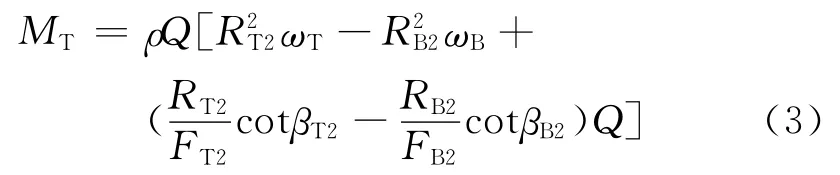
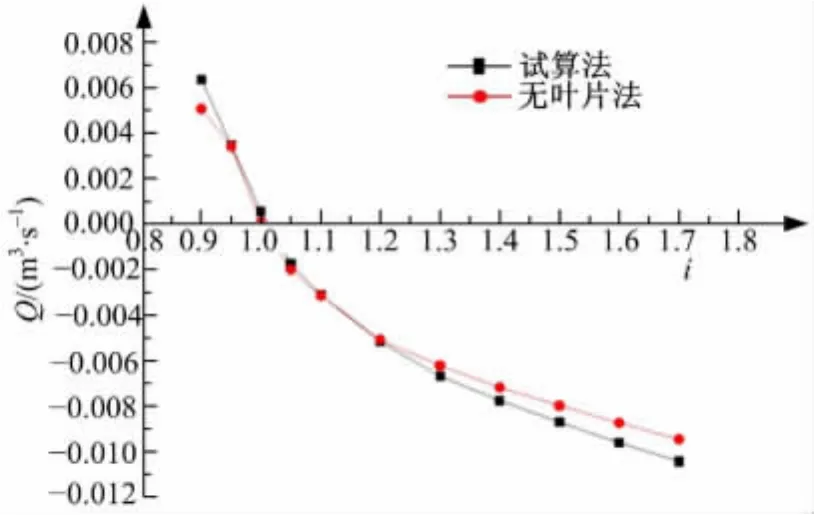
图7 用两种方法计算出的循环流量值Fig.7 Circulation flow calculated by two methods

式中：MT为涡轮液力转矩；Q为循环流量（计算时以其绝对值代入）；RB2、RT2为泵轮和涡轮循环圆出口半径；FB2、FT2为泵轮和涡轮循环圆出口处与轴面速度相垂直的流道截面积；βB2、βT2为泵轮和涡轮叶片出口角。所研究变矩器的参数取值如下：RB2＝0.215m；RT2＝0.039m；FB2＝0.051 m2；FT2＝0.051m2；βB2＝65°；βT2＝150°。

根据变矩器的参数，在对应导轮空转的变矩器速比范围（0.85＜i＜1.0和i＞1.0）内，不难得到：

即涡轮转矩绝对值是循环流量绝对值的递减函数，因此用无叶片法计算出的循环流量绝对值偏小，必然造成转矩值偏大。可见，无叶片法仿真计算结果与经典束流理论的预期相符。

无叶片法由于保持了导轮内、外环面的导流作用，忽略了导轮叶片的导流作用，因而不需要设定导轮转速（默认为0），也不需要像试算法那样反复修改导轮转速进行试算。无叶片法虽不能直接获得导轮的空转转速值，但在导轮空转时转矩为零的假设下，导轮空转转速应该与导轮工作腔内部流体的绝对速度在圆周方向的分量相等，为此可以从导轮工作腔内提取有代表性的空间点作为导轮流体圆周分速度的监控点，这些质点分别记为Point＿A、Point＿B、Point＿C、Point＿D、Point＿O，这5个点在导轮工作腔内的位置如图8所示，图8（a）显示的是5个监控点在轴面内的对应位置，图8（b）显示的是5个监控点在流道中的对应位置。

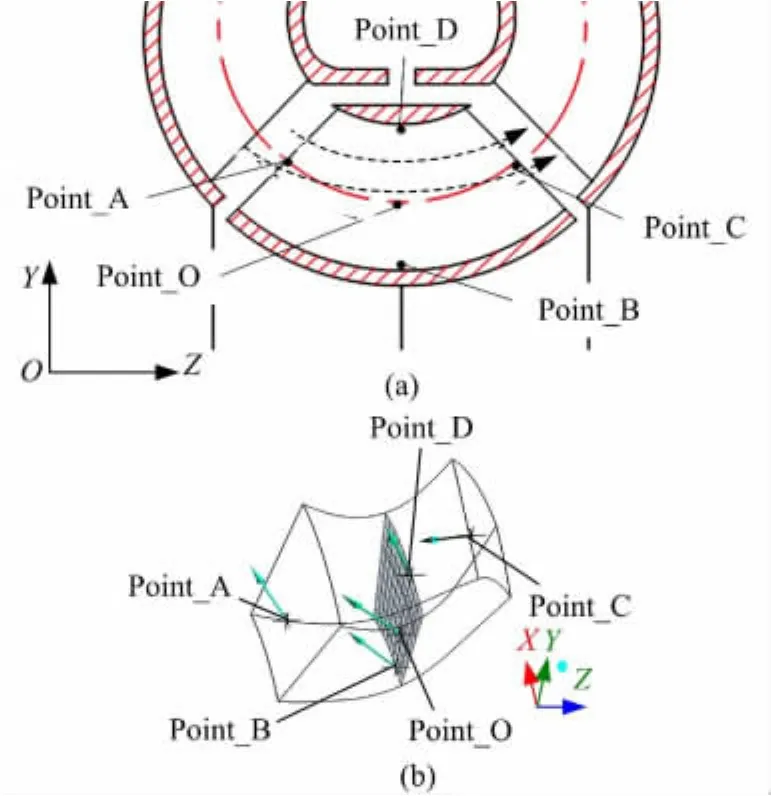
图8 5个监控点的位置布置Fig.8 Position layout of five monitoring points

从无叶片仿真结果中分别提取上述5个监控点的流体圆周分速度，其随变矩器转速比的变化情况如图9所示。图9中S曲线是用试算法获得的导轮转速，易知在转速比为1.0附近，监控点圆周分速度变化剧烈，在其余转速比位置变化平缓。这是由于在转速比为1.0附近，变矩器循环流量方向改变（见图7），工作液体处于正、反循环的过渡阶段，流动状态极不稳定所致。在转速比小于1.1时，位于导轮叶片出口面的监控点Point＿C的圆周速度与试算法结果最接近，这是由于在耦合器工况流动状态恶化，导轮入口以及导轮腔内流体在转动方向不容易与导轮实现同步，而Point＿C处于导轮出口，是液流正循环的终点，流体经过与导轮的充分作用其旋转速度与导轮转速最接近。

在转速比大于1.1以上较宽广的转速比范围内，稳定的反循环已经建立，5个监控点处的流体圆周分速度与用试算法得到的转速值走势保持一致，其中位于导轮中间面上的监控点Point＿O的圆周分速度与用试算法获得的导轮转速值非常接近，二者误差始终在3%以内，监控点Point＿O在Y方向（见图8（a））的速度分量近似为0，在流动稳定的转速比范围内，其绕Z轴方向的转速与导轮的空转转速最接近。

基于上述分析，利用无叶片法确定导轮空转转速时，在牵引工况的偶合器阶段（转速比0.85～1.0）应取导轮出口处的Point＿C监控点来观测导轮转速，在反转工况（转速比大于1.0），应取导轮中间截面处的监控点Point＿O来观测导轮转速。在上述监控点位置序列下，由无叶片法确定出的导轮转速如图10所示，图中n代表相应导轮转速，后缀polyfit代表由数据点采用最小二乘法进行3次多项式拟合的曲线，后缀bladeless代表无叶片法结果。从图10可以看出两种方法确定出的导轮转速的拟合曲线较为接近，二者误差小于5%。

图10 无叶片法和试算法确定出的导轮转速值Fig.10 Stator wheel’s speed calculated by two methods

无叶片法通过采用选择监控点的方法确定出导轮转速，在作反转工况研究时，可以直接采用导轮工作腔中间截面处Y速度分量为零的点（见图8（a）中Point＿O位置）作为导轮转速的监控点，这样可以方便地确定相应的导轮转速。

5 结 论

（1）通过与传统零转矩试算法的仿真结果对比，可以看出基于对导轮导流作用分析提出的无叶片仿真方法是合理可行的。无叶片法在预测导轮空转工作特性方面具有与试算法相接近的仿真精度，但无需反复试算，大大节省了计算时间和工作量，具有一定的工程实用价值。

（2）无叶片仿真方法不但可以直接确定导轮空转时变矩器的变矩特性、循环流量特性，而且还可以通过设定监控点来间接确定导轮转速，为变矩器空转轮工作特性研究提供了一种新思路。

［1］刘春宝，马文星，朱喜林.液力变矩器三维瞬态流场计算［J］.机械工程学报，2010，46（14）：161－166.Liu Chun－bao，Ma Wen－xing，Zhu Xi－lin.3Dtransient calculation of internal flow field for hydrodynamic torque converter［J］.Journal of Mechanical Engineering，2010，46（14）：161－166.

［2］刘春宝，马文星，许睿.液力变矩器轴向力的CFD计算与分析［J］.吉林大学学报：工学版，2009，39（15）：1181－1185.Liu Chun－bao，Ma Wen－xing，Xu Rui.Calculation and analysis of axial force in hydrodynamic torque converter based on CFD［J］.Journal of Jilin University Engineering and Technology Edition，2009，39（5）：1181－1185.

［3］项昌乐，肖荣，阎清东，等.牵引－制动型液力变矩器流场分析［J］.工程机械，2005（5）：43－46／110.Xiang Chang－le，Xiao Rong，Yan Qing－dong，et al.An analysis on flow feild in hydraulic converter of drive／brake type［J］.Construction Machinery and Equipment，2005（5）：43－46／110.

［4］张锡杰.液力变矩器三维流场数值分析及性能预测研究［D］.上海：上海交通大学，2009.Zhang Xi－jie.Research on 3－dimensional flow field numerical simulation and performance prediction of hydrodynamic torque converter［D］.Shanghai：Shanghai JiaoTong University，2009.

［5］才委.双涡轮液力变矩器转矩分配特性研究［D］.长春：吉林大学机械科学与工程学院，2009.Cai Wei.Research on the torque distribution characteristies of dual－turbine torque converter［D］.Changchun：College of Mechanical Science and Engineering，Jilin University，2009.

［6］魏巍，闫清东，马越.液力变矩－减速装置制动性能流场数值模拟研究［C］∥中国汽车工程学会越野车技术分会2008年学术年会论文集，西安，2008：212－215.

［7］Launder B E，Spalding D B.Lectures in Mathmatical Models of Turbulence［M］.New York：Academic Press，1972.

［8］Fluent Inc.FLUENT User＇s Guide［M］.New York：Fluent Inc，2003.

［9］王福军.计算流体动力学分析——CFD软件原理与应用［M］.北京：清华大学出版社，2004.

［10］才委，马文星，褚亚旭，等.液力变矩器导轮流场数值模拟与试验［J］.农业机械学报，2007（8）：11－14.Cai Wei，Ma Wen－xing，Chu Ya－xu，et al.Numerical simulation and experimental research on flow field in the stator of a torque converter［J］.Transactions of the Chinese Society for Agriculture Machinery，2007（8）：11－14.

［11］朱经昌，魏宸官，郑慕侨，等.车辆液力传动［M］.北京：国防工业出版社，1982.