基于交叉口多相位信号控制的路网容量

王 建 邓 卫

(东南大学交通学院，南京 210096)

信号控制路网容量问题是指在考虑用户路径选择条件下，如何选择信号配时参数使路网容量达到最大［1］.路网容量研究具有重要的现实意义，可以减少不必要的道路建设，帮助决策者进行信号参数优化选择，使得路网能承载高峰时段居民出行需求，还可以预先决定城市各片区土地利用强度，以充分挖掘现有路网的通行能力.

Wong等［2］首次探讨了用户均衡条件下的路网备用容量问题，建立了双层规划模型，模型采用灵敏度分析法求解.Gao等［3］拓展了路网容量的定义，改进了Wong等［2］设计的模型，认为路网O-D需求乘子的增长倍数不一定相同，具体算例显示在该定义下路网可以获得更大的备用容量.张鹏等［1，4］将信号延误引入交通分配模型中，探讨了考虑信号延误下的路网容量问题，并且进一步研究了车道分配对路网容量的影响，通过分配道路双向车道数、优化信号配时参数等措施，达到增大路网容量的目的.Chiou［5］研究了信号控制路网总延误最小目标下的路网备用容量问题，并利用投影拟牛顿法进行求解.在上述研究中，用以描述驾驶人择路行为的交通分配模型都是以简单的两相位信号控制为基础的，而在实际城市道路网络中，为了减少交叉口左转车流与对向直行车流的冲突，交叉口大都采用三相位以上的信号进行控制，故上述研究中的交通分配模型不能描述多相位信号控制路网中驾驶员的路径选择行为，即对于交叉口多相位信号控制的城市道路网络，上述容量模型欠缺实用性.

为了提高路网容量模型的实际可操作性，本文建立了一种描述多相位信号控制路网容量的双层规划模型.其中，下层模型是交叉口多相位信号控制路网交通分配模型，该模型遵循Wardrop用户均衡条件;上层模型是信号控制参数优化模型，通过优化各个交叉口绿信比、周期时间以及O-D需求量，达到路网容量最大化的目标.双层规划模型采用基于灵敏度分析的启发式算法求解.

1 多相位信号控制路网容量模型

1.1 多相位信号控制路网用户均衡分配模型

传统的信号控制路网交通分配模型虽然考虑了路段的信号延误，但都假设路网中各个交叉口由简单的两相位信号进行控制.在多相位信号控制路网中，由路段进入交叉口的各个流向流量和对应的信号延误均不相同，交通分配模型需要对各相位下的流量和延误加以区分.根据文献［6-7］中交叉口多相位信号控制路网的驾驶员择路行为，构建出多相位信号控制路网的用户均衡交通分配模型，即

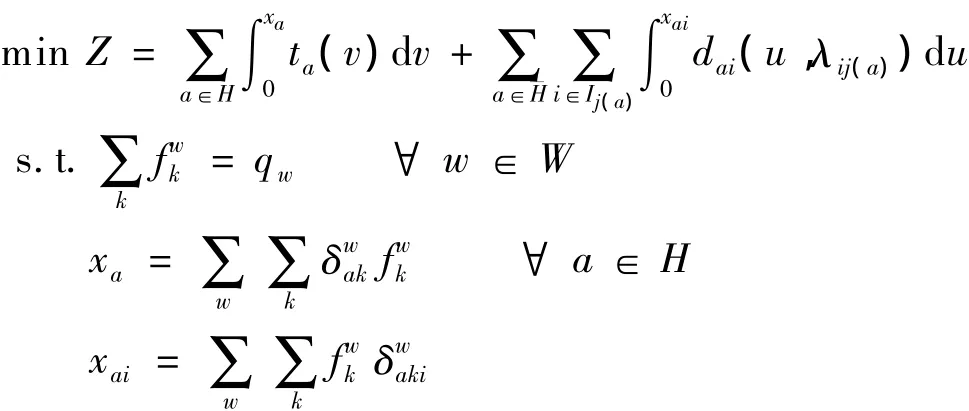
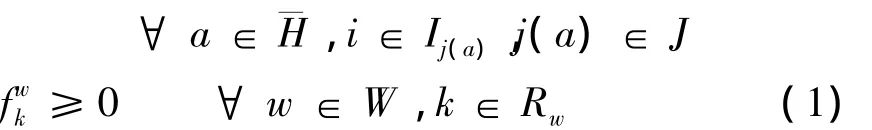
式中，Z为目标函数;w为路网中的一个O-D对;xa为路段a的总流量;ta为路段a的行驶时间;H为路网中所有路段的集合为进入信号控制交叉口路段的集合;j(a)为路段a对应的交叉口;Ij(a)为交叉口j(a)的信号相位集合;xai为路段a在交叉口j(a)处第i个相位的流量;dai为路段a对应的第i个相位的信号延误;λij(a)(i=1，2，…，n)为路段 a对应信号交叉口各相位的绿信比;W为路网中所有O-D对的集合为O-D对w之间第k条路径上的流量;J为路网中信号控制交叉口的集合;qw为O-D对w之间出行需求量;Rw为O-D对w之间所有路径的集合为路段-路径连接关系变量，当O-D对w之间第k条路径经过路段a时1，否则=0;为路径-路段转向关系变量，当O-D对w之间第k条路径经过路段a，且转向后归入路段a上的第i相位车流时=1，否则=0.给定交通网络结构图时，路径-路段转向关系变量容易确定，故可以求得路段在各个相位下的车流量.

文献［7-8］证明了模型(1)满足Wardrop用户均衡条件，是一种用户最优的交通均衡分配模型，存在唯一的极值.可采用罚函数和逐步回归等方法对该模型求解.

根据文献［9］，目标函数中信号交叉口各相位的信号延误可表示为

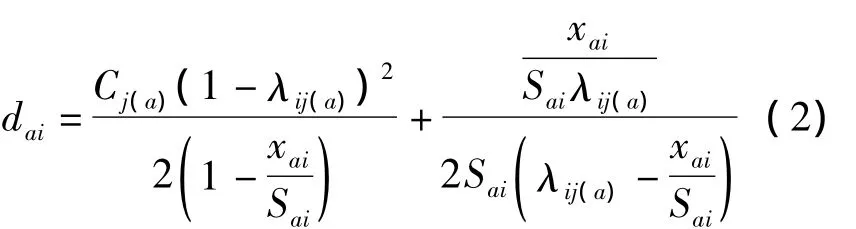
式中，Cj(a)为交叉口j(a)的信号周期;Sai为路段a中第i相位放行车道的饱和流量.

1.2 信号控制交叉口约束模型

假设进入交叉口存在左转交通量的路段都设有左转相位以及左转专用车道.对单个信号控制交叉口进行优化配时时，各相位的有效绿灯时间应满足交叉口相应流向流量的通行需求，信号控制设置必须使路段各相位的流量不超过该相位放行方向上设置车道的通行能力，即

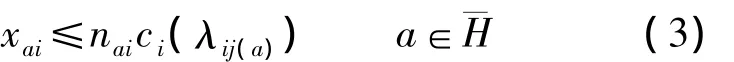
式中，nai为路段 a中第 i相位的放行车道数;ci(λij(a))为路段a中第i相位放行方向单个车道的通行能力.由于xai是在给定路网O-D需求量、周期时间以及绿信比下模型(1)的均衡分配结果，因此可以将其表示为路网O-D需求量、周期时间和绿信比的函数，则式(3)可以写成

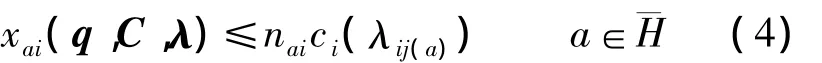
式中，q为所有O-D需求向量;C为路网交叉口周期时间向量;λ为绿信比向量.

此外，信号周期时间和绿信比必须满足如下的边界约束:

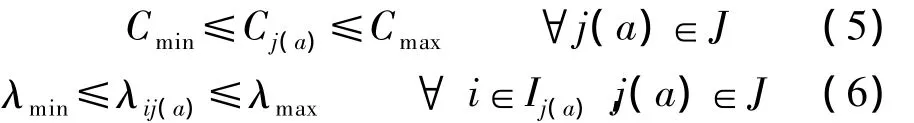
式中，Cmin，Cmax分别表示周期时间的下限和上限;λmin，λmax分别表示绿信比的下限和上限.

一般而言，随着经济、人口的增长，各个小区的用地强度也会出现相应变化.假设这种O-D需求的变化不存在极端情况，即某个O-D对之间的需求为0，则各O-D出行需求量必须满足如下的下界约束:

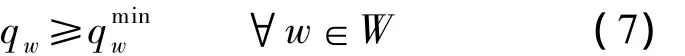
由于交叉口损失时间的存在，对一个信号交叉口 j(a)，有

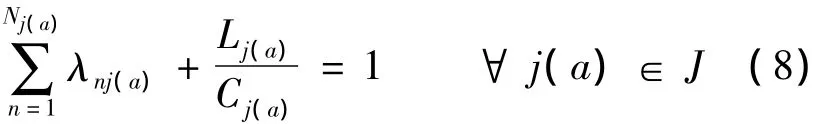
式中，Lj(a)为交叉口j(a)一个周期的损失时间;Nj(a)为交口j(a)的相位总数.

1.3 双层规划模型

多相位信号控制路网容量可以表示为

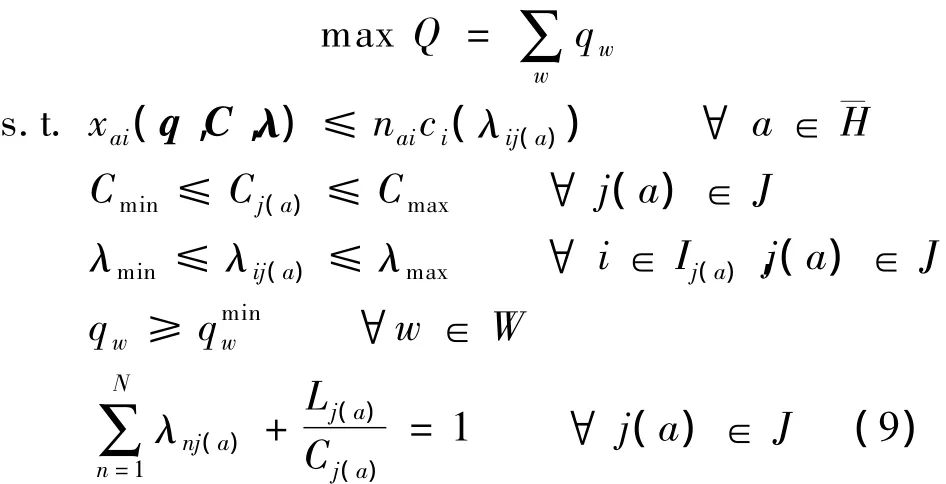
式中，Q表示路网出行需求总量.xai(q，C，λ)可通过求解多相位信号控制路网用户均衡分配模型(1)得出.

2 模型求解算法

多相位信号控制路网容量模型是一个双层规划模型.鉴于双层规划模型的非凸性，全局最优解难以求得.此外，在最大路网容量模型中，上层模型xai(q，C，λ)是一个非线性模型，并且函数形式未知，因而不能直接求解约束规划方程.文献［1-4］采用灵敏度分析方法求解类似双层规划模型，即在路网变量(O-D需求量、周期时间以及绿信比)相互独立的条件下，对下层用户均衡交通分配模型进行灵敏度分析，得到路段均衡流量对路网变量的导数，从而将上层模型中路段流量函数转换成线性函数进行求解.但是，对于用户均衡分配模型(1)，需要考虑各相位下路段流向流量，并且路径-路段连接关系矩阵是一个三维矩阵，故传统灵敏度分析方法并不适用.

灵敏度分析的目的是为了获得均衡状态下路段流量对各个路网设计变量的导数.导数是函数在自变量变化处的变化率，可以看作函数的微分与自变量的微分之商即微商，而微商是差商的极限形式［10］，因此可通过差商的方法近似估计出路段流量对设计变量的导数.这种方法不需要假设路阻函数是路段流量的单调递增函数，相比于经典的灵敏度分析方法，其应用范围更为广泛.利用差商的方法求解均衡状态下信号控制路段各流向流量对设计变量导数的过程如下:假设xai是模型(1)在控制参数(q*，C*，λ*)处的一个均衡解，将路网变量qw在初始值的基础上增加Δqw，其他变量不变，求得变量qw变化后模型(1)的均衡解.设此时xai的均衡解相比于初始值增加了Δxai，则xai在控制参数(q*，C*，λ*)处对变量qw的导数可以估计为Δxai/Δqw.采用类似的方法可求出 xai对其他路网设计变量的导数.则路网容量上层模型中未知函数xai(q，C，λ)可近似表示为如下的线性形式:

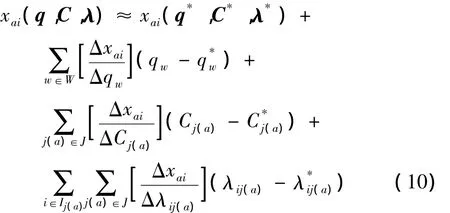
将式(10)代入上层模型中，则上层模型变为一个以O-D需求量、周期时间和绿信比为变量的普通非线性优化模型，可以采用序列二次规划法求解.根据上层模型求得的最优解，再一次求解下层交通分配模型，得到新的路段均衡流量;重复上述过程，就可以得到新的路网容量.如此反复计算，有望收敛于路网容量双层规划模型的最优解.这种基于灵敏度求解双层规划模型的方法称为BLABD算法，算法过程参见文献［10］.

3 算例分析

图1为信号控制路网结构图.由图可知，该路网包含6个节点、3个 O-D 对(A-B，B-A，C-D)和10个路段.其中，节点E和节点F为信号控制交叉口，每个O-D对之间有2条可选的路径.由于路径A-F-E-B以及B-E-F-A需要在相应的路口左转，故在路段2和路段8上设置专用左转车道以及专用左转相位.C-D方向没有左转车辆，故只设置1个相位放行直右方向的车辆.交叉口E和交叉口F的相位设置如图2所示.路段2和路段8设置2个车道，分别为左转专用车道和直右车辆放行车道，其他所有路段均只设置1个车道，单个车道的通行能力为1800 pcu/h.路段行驶时间可表示为

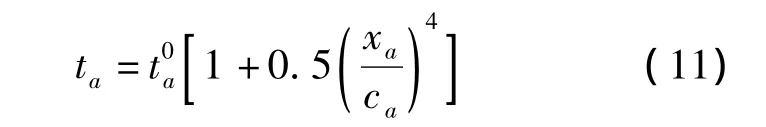
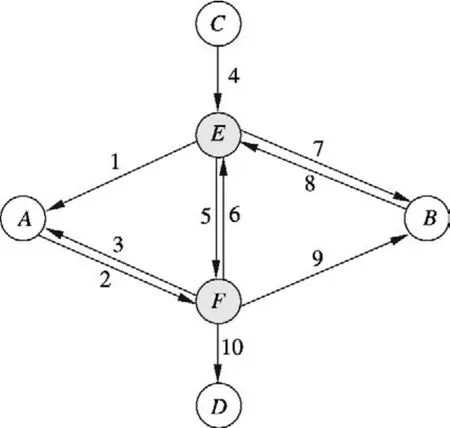
图1 信号控制路网结构图

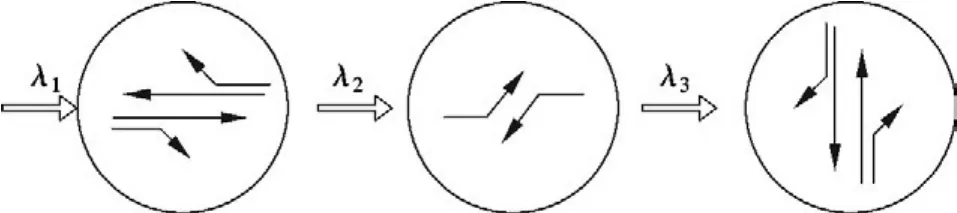
图2 交叉口E和F的相位设置

利用Matlab编程求解图1所示的基于多相位的最大路网容量问题，取收敛精度 ε1=ε2=ε3=0.001，O-D出行需求量、周期时间以及绿信比的增加量分别设为 10，5，0.05.经过 7次迭代，计算结果满足收敛精度要求.各次迭代结果见表2.

由表2可知，第4次迭代结果已经接近均衡解，说明BLABD算法收敛速度较快.到达稳定解时，路网容量为2338.687 pcu/h，即在现有 O-D出行总量下，路网可以多容纳94.89%的O-D出行量.最大路网容量下，O-D对A-B之间的最大出行量为994.518 pcu/h，较初始值增加 98.90%;O-D对B-A的最大出行量为1074.580 pcu/h，即在到达路网容量前，B-A出行量还可以多容纳114.92%的O-D出行量;最大路网容量状态下，O-D对C-D之间的出行需求量为269.589 pcu/h，较初始值增加34.79%.达到路网最大容量时，交叉口E各信号相位的有效绿灯时间分别为 33.08，5.87，9.77 s;交叉口F各信号相位的有效绿灯时间分别为33.39，13.90，22.26 s.表 3 给出了最大路网容量下的路径流量和行驶时间.由表可知，O-D对A-B和B-A之间的各条路径具有相同的行驶时间，而O-D对C-D之间的出行需求量全部分布在最短路径C-EF-D中，即所有使用的路径具有相同的行驶时间，未使用路径的行驶时间大于使用路径的行驶时间，因此分配结果符合用户均衡准则.需要注意的是，BLABD算法中每一次迭代都需要多次求解下层用户均衡分配模型，故对于设计变量较多的大型路网，该算法的实用性会相应降低.

表1 各交叉口信号参数和O-D需求量的初始值

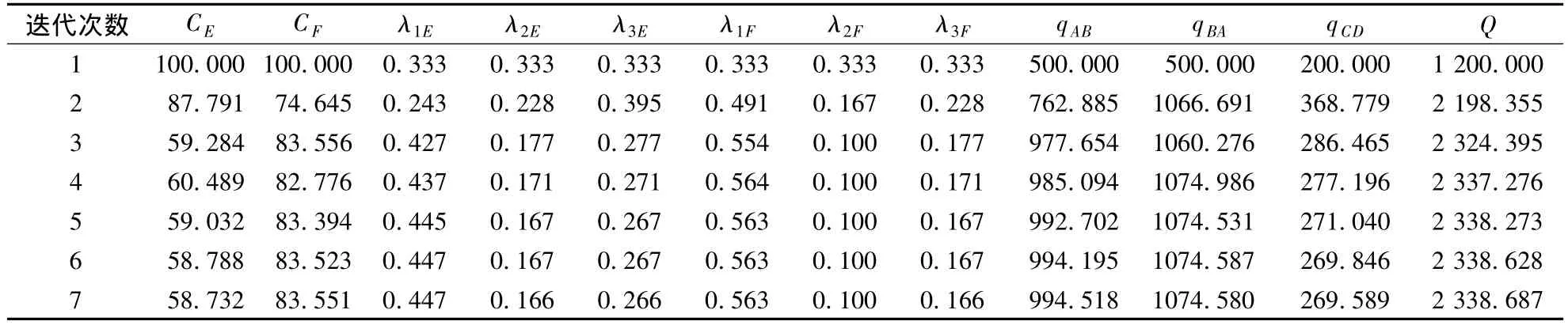
表2 各次迭代中O-D需求量、周期时间、绿信比的计算结果

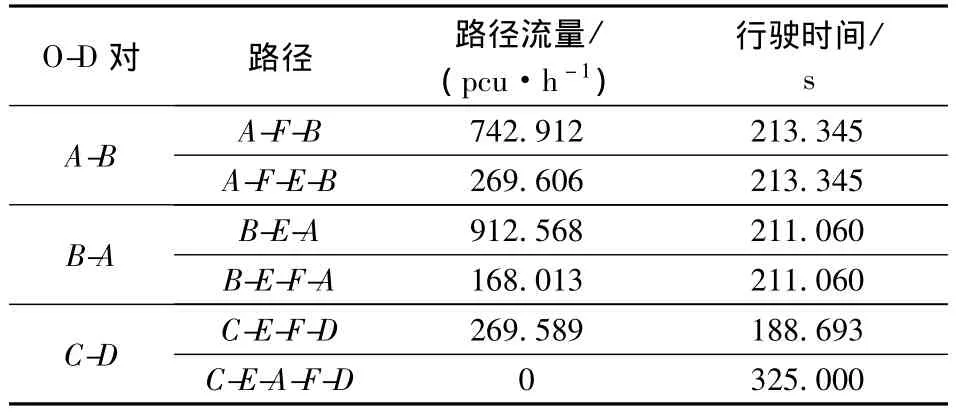
表3 最大路网容量下的路径流量和行驶时间

4 结语

本文建立了一种交叉口多相位信号控制路网容量的双层规划模型.为了克服传统灵敏度分析方法的局限，采用BLABD算法来求解路网容量模型.该算法通过差商的方法近似估计均衡状态下信号控制路段各流向流量对设计变量的导数，将上层模型中的车道饱和度约束方程转化为线性方程，进而求解.算例分析结果表明，BLABD算法可有效求解多相位信号控制路网容量问题.但是在计算中发现，利用差商方法进行灵敏度分析时需要多次求解设计变量变化后的用户均衡解，模型计算量较大，计算速度相对较慢，因此对于大型路网容量问题，有必要研究新的求解多相位信号控制路网模型的方法.

References)

［1］张鹏，李文权，常玉林.考虑交叉口延误的信号控制路网容量模型［J］.东南大学学报:自然科学版，2009，39(4):863-866.Zhang Peng，Li Wenquan，Chang Yulin.Capacity model of signal-controlled road network taking account of delay of intersections［J］.Journal of Southeast University:Natural Science Edition，2009，39(4):863-866.(in Chinese)

［2］Wong S C，Yang H.Reserve capacity of a signal-controlled road network ［J］.Transportation Research Part B:Methodological，1997，31(5):397-402.

［3］Gao Ziyou，Song Yifan.A reserve capacity model of optimal signal control with user-equilibrium route choice［J］.Transportation Research Part B:Methodological，2002，36(4):313-323.

［4］张鹏，李文权，常玉林.可变车道的城市路网备用容量模型［J］.西南交通大学学报，2010，45(2):255-260.Zhang Peng，Li Wenquan，Chang Yulin.Reserve capacity model for urban road network with variable lanes［J］.Journal of Southwest Jiaotong University，2010，45(2):255-260.(in Chinese)

［5］Chiou Suhwen.A hybrid approach for optimal design of signalized road network ［J］.Applied Mathematical Modelling，2008，32(2):195-207.

［6］刘灿齐.专适于城市道路网络的交通均衡分配模型［J］.公路交通科技，2003，20(6):97-100.Liu Canqi.Traffic equilibrium assignment model special for urban road network［J］.Journal of Highway and Transportation Research and Development，2003，20(6):97-100.(in Chinese)

［7］黄崇超，李亚萍.考虑交叉口信号延误的平衡交通分配模型［J］.武汉大学学报:工学版，2009，42(3):373-376.Huang Chongchao，Li Yaping.Equilibrium assignment models with intersections signal delay［J］.Engineering Journal of Wuhan University，2009，42(3):373-376.(in Chinese)

［8］刘灿齐.城市道路网络交通信号协调控制的优化［J］.同济大学学报:自然科学版，2004，32(8):1000-1004.Liu Canqi.Integral optimizing method of traffic signal on network of urban road［J］.Journal of Tongji University:Natural Science Edition，2004，32(8):1000-1004.(in Chinese)

［9］Ying Jiangqian，Lu Huapu，Shi Jing.An algorithm for local continuous optimization of traffic signals［J］.European Journal of Operational Research，2007，181(3):1189-1197.

［10］高自友，宋一凡，四兵锋.城市交通连续平衡网络设计:理论与方法［M］.北京:中国铁道出版社，2000.