实时混合模拟频域评价方法的物理意义

徐伟杰 郭 彤 陈 城

(1东南大学土木工程学院，南京 210096)

(2旧金山州立大学工程学院，旧金山 94132)

实时混合模拟是一种新型的动力试验方法［1］.该方法可实现结构在足尺条件下的实时加载，能够全面反映其动力特性，因而在近年来得到广泛关注和快速的发展［2-7］.由于伺服系统的动力特性，作动器总是不能绝对实时地达到预定的位移，而是存在一个“时滞”，如果不能进行合理的补偿，将会导致试验失败.因此，实时混合模拟结果的有效性评价是该试验技术的核心内容之一.文献［8］提出了一种频域评价方法，将实时混合模拟的误差分为幅值误差和相位误差，通过引入等效频率的概念，可定量计算出实时混合模拟的时滞，该方法与传统的时域评价方法相比，具有一定的优越性［9-13］.然而，作为一种新的评估手段，该方法的物理意义目前尚不够明确.本文通过数值模拟和实验室试验，分别对线性和非线性子结构进行分析，并对该方法的物理意义做出剖析.

1 频域评价方法

本文涉及的实时混合模拟的频域评价方法是一种双参数方法［8］，分别采用参数A和d对试验的幅值和时滞进行评估，即

式中，A和d分别表示实时混合模拟的幅值和等效时滞;‖·‖表示求模;FEI为频域评价指标;φ表示实时混合模拟的相位差，可分别按下式计算:

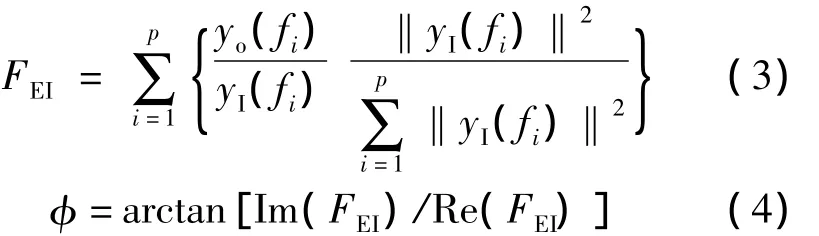
式中，yI(f)和yo(f)为输入和输出的傅里叶变换，一般取计算位移作为输入，测量位移作为输出;p为分析数据的一半;feq表示等效频率，通过对输入进行傅里叶变换，再将得到的频率按照该频率的幅值平方进行加权，即

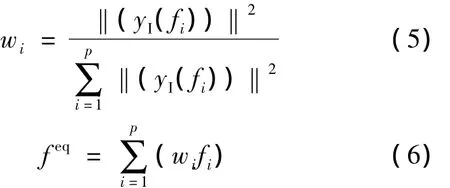
式中，wi和fi为第i个频率的权重和大小.在输入和输出进行傅里叶变换之前，为消除频谱泄露的影响，可乘上一个窗函数［14］(如汉宁窗).

理想情况下，输入与输出没有任何误差，此时φ和d应为0，且A为1.幅值A与1的误差称为幅值误差，相位φ与0的误差称为相位误差.幅值误差和等效时滞的绝对值越小，实时混合模拟的效果越好.

按照实时混合模拟评价方法的基本思路，同样可以计算出每一个频率的幅值、相位和等效时滞［8］，即

式中，Aj，φj，dj和 fj分别为第 j个频率下的幅值、相位、等效时滞和频率.需要注意的是，式(8)计算得到的相位取值范围在±π之间，当信号频率较高时，计算得到的相位可能与实际相位存在误差(相差若干个2π).

2 数值模拟

2.1 试验子结构为线性结构

首先，利用Matlab软件的 Simulink模块［14］进行数值模拟研究.当试验子结构为线性结构时，设结构的自振频率为1 Hz，质量m取1000 kg，结构阻尼比为 0.02.根据 Wallace 等［15］的研究，此时结构保持稳定的临界时滞为6.4 ms，故实时混合模拟的时滞选择为5 ms，且在模拟过程中不采用补偿环节.为了证明实时混合频域评价方法能够区分幅值误差，令模拟的测量位移与指令位移之间存在一个1.1的幅值误差.此时，实时混合模拟的Simulink模型如图1所示，为了防止积分算法对模拟的影响，采用运动方程的转换函数来代替积分算法.地震波选择水平分量为CHY101-N的Chi-chi地震波，其峰值加速度为0.4401g.

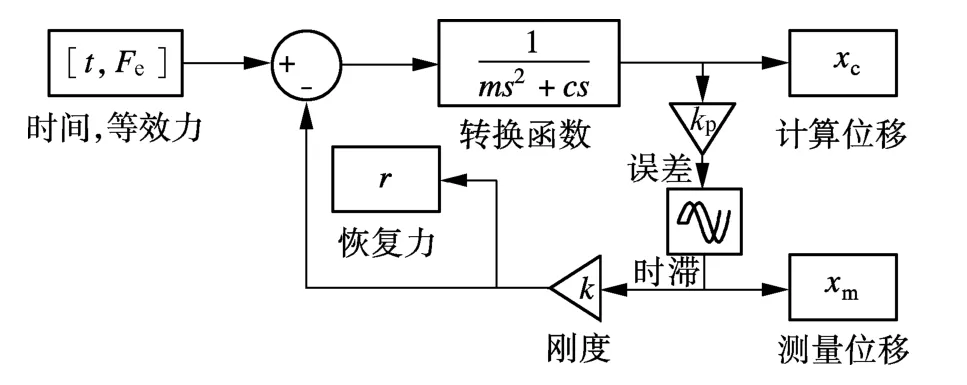
图1 实时混合模拟的Simulink模型

采用实时混合模拟频域评价方法，将计算位移作为输入，指令位移作为输出，得到的幅值、相位和等效时滞分别为1.1，－0.0326 rad和5 ms，这与理论值完全相同.为研究频域评价方法的物理意义，根据式(7)～(9)和式(5)分别计算出每个频率的幅值、相位和等效时滞以及每个频率在加权时的权重，如图2所示.由图2(a)可见，对于幅值A，除在高频处存在突变外，其他数值整体上较为平稳;而由图2(b)可以发现，相位φ着随频率的增加而近似呈周期性变化，这是由于式(8)计算得到的相位只能在±π之间，当相位超过±π时，计算得到的高频相位要比实际相位大若干个2π.因此，当频率在较低的范围内时，计算得到的等效时滞约为5 ms，而当频率较大时，时滞将出现震荡，如图2(c)所示.由于图2(b)中每一段相位都是随频率增加而线性减小，故理论上时滞在各个频率上仍然为5 ms左右.然而，由图2(d)可以发现，权重主要集中在低频段，故在频域评价方法中，高频处相位和时滞计算的误差可以忽略.

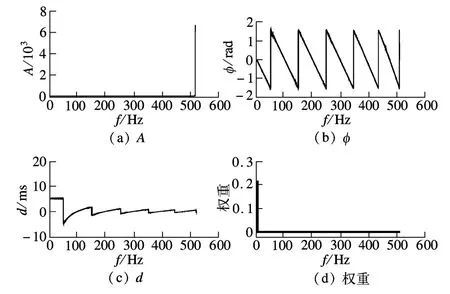
图2 线性结构频域评价方法在各个频率上的指标

图3进一步给出了低频区的频域分析结果.由图3(a)可以发现，低频上的幅值并非是1.1，但是相差非常小;而图3(b)中的相位也不是一条直线.当频率稍大于0 Hz时，计算得到的时滞与5 ms相差较大，相差部分的时滞称为“虚假时滞”，随频率的增加，时滞很快收敛到5 ms，如图3(c)所示.虚假时滞主要集中在前3个频率，这可能是由于傅里叶变换引起的，当前3个频率权重不大时，该虚假时滞对等效时滞不会产生影响，当前3个频率权重较大时(主要指非线性结构)，会对时滞产生较大影响，所以应在加权时将前3个频率的计算结果舍去.此外，由于实时混合模拟过程中存在1.1的幅值误差，因此结构的等效频率要稍微大于1 Hz，如图3(d)所示.

图3 线性结构频域评价方法在低频上的指标

对于每个频率，在计算其幅值Aj、相位φj和时滞dj时，按照该频率的权重wj进行加权，由此得到综合的幅值A'、相位φ'和等效时滞d'，即

由式(10)～(12)计算得到的幅值A'、相位φ'和等效时滞 d'分别为 1.1，－0.0326 rad和5 ms，与采用频域评价方法直接计算得到的幅值、相位和等效时滞完全相同.因此，实时混合模拟的频域评价方法实质上是计算出各个频率的幅值和相位，并按照各频率输入幅值平方的权重进行加权.

2.2 试验子结构为非线性结构

当结构为非线性结构时，采用与线性结构相同的模型和参数，但用 Bouc-Wen模型［16］来代替试验子结构的刚度k，Bouc-Wen模型计算恢复力的方法为

式中，xy为数结构的屈服位移，xy=10 mm;k为结构的线弹性刚度，k=11.75 kN/mm;η为数值子结构屈服前后的刚度比，η=0;x(t)为施加在数值子结构上的位移;z(t)为Bouc-Wen参数，由以下方程得到:

式中，β，γ，q为控制滞回曲线形状的参数，其值分别为0.55，0.45和2.由于非线性有助于提高结构的稳定性，故模拟在5 ms的时滞下仍然会保证稳定.采用实时混合模拟频域评价方法，将计算位移作为输入，指令位移作为输出，得到的幅值、相位和等效时滞分别为1.1，－0.0033 rad和5 ms.由于结构的非线性会降低结构刚度，因此非线性结构的相位小于线性结构的相位.根据式(6)～(8)分别计算出每个频率上的幅值、相位和等效时滞以及每个频率在加权时的权重，如图4所示.

与线性结构类似，幅值A除在高频处存在突变外，总体上较为平稳，如图4(a)所示.与图2(b)相比，图4(b)中的相位φ不再随频率做周期性变化.由于式(8)计算得到的相位只能在±π之间，因而高频范围内的等效时滞计算结果并不准确.当频率较低时，计算得到的等效时滞在5 ms左右，而当频率较大时，时滞同样出现震荡现象，如图4(c)所示.由图4(d)可发现，权重主要集中在低频段，故在频域评价方法中，高频处相位和时滞计算的误差同样可被忽略.图5给出了低频区段的计算结果.

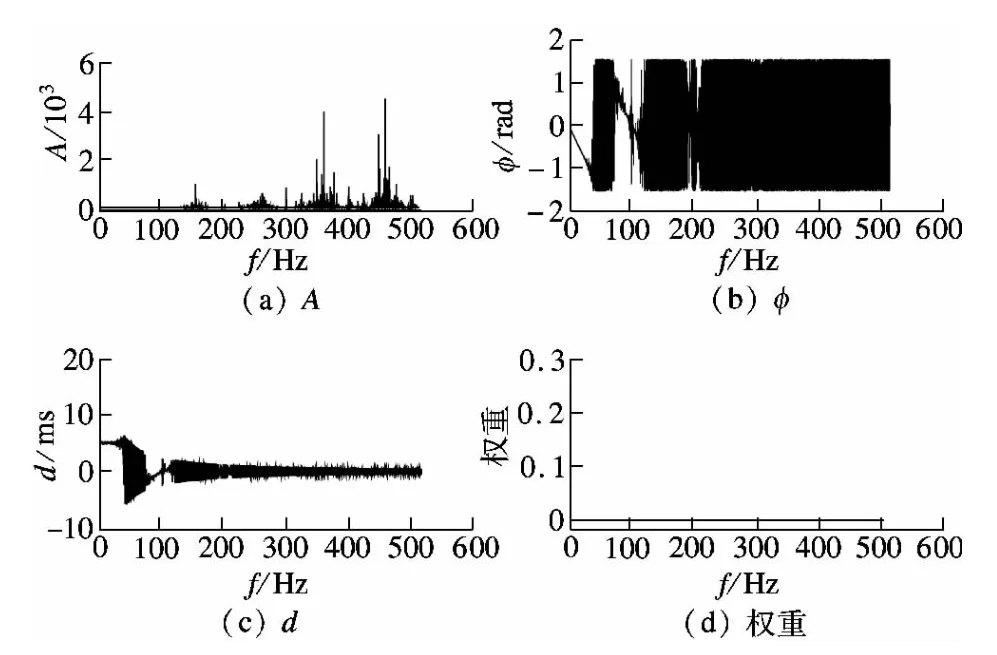
图4 非线性结构频域评价方法在各个频率上的指标

图5 非线性结构频域评价方法在低频上的指标

非线性结构的幅值A、相位φ和等效时滞d与线性结构类似，如图5(a)～(c)所示.然而，非线性结构的权重主要集中在0.1 Hz附近，明显小于线性结构的情况(见图3(d)，集中于1.0 Hz)，这是由于结构的非线性会造成刚度退化，从而降低了结构的等效频率，如图5(d)所示.同时，虚假时滞范围内的频率权重不大，对等效时滞的影响可忽略.

采用式(10)～(12)计算得到综合的幅值A'、相位 φ'和等效时滞 d'分别为1.1，－0.0033 rad 和5 ms，与采用频域评价方法直接计算得到的幅值、相位和等效时滞完全相同，进一步证明了实时混合模拟的频域评价方法实质上是计算出各个频率的幅值和相位，并按照各频率输入幅值平方的权重进行加权.

3 试验验证

为进一步验证频域评价方法的物理意义，利用Lehigh大学完成的实时混合模拟试验数据进行分析［13］.其中，数值子结构采用多自由度的钢框架，其质量为5.034×105kg，结构自振频率为0.77 Hz，阻尼比为0.02.试验子结构采用洛德(LORD)公司生产的磁流变(MR)阻尼器.阻尼器的长度为1.47 m，冲程为584 mm，最大工作荷载为200 kN.整个试验装置由阻尼器、作动器、反力架等依次串联而成.动态作动器的最大输出荷载为1700 kN，冲程为500 mm，最大运动速率为760 mm/s，伺服控制器采用PID控制，其中比例增益为20，积分增益为4，微分增益为0，采样频率为1024 Hz.积分算法采用 CR算法［3］，补偿方法采用倒转补偿法［4］，预测时滞为 29 ms.

由于试验子结构为非线性结构，根据式(7)和(8)分别计算出每个频率上的幅值、相位和等效时滞以及每个频率的权重，如图6所示.由图可以发现，实时混合模拟的幅值变化规律与非线性结构较为相似，而图6(b)中相位在低频波动要比数值模拟更为明显，这同样造成了时滞在低频的波动，如图6(c)所示.由图6(d)还可以发现，权重主要集中在低频段.图7给出了低频区段的计算结果.

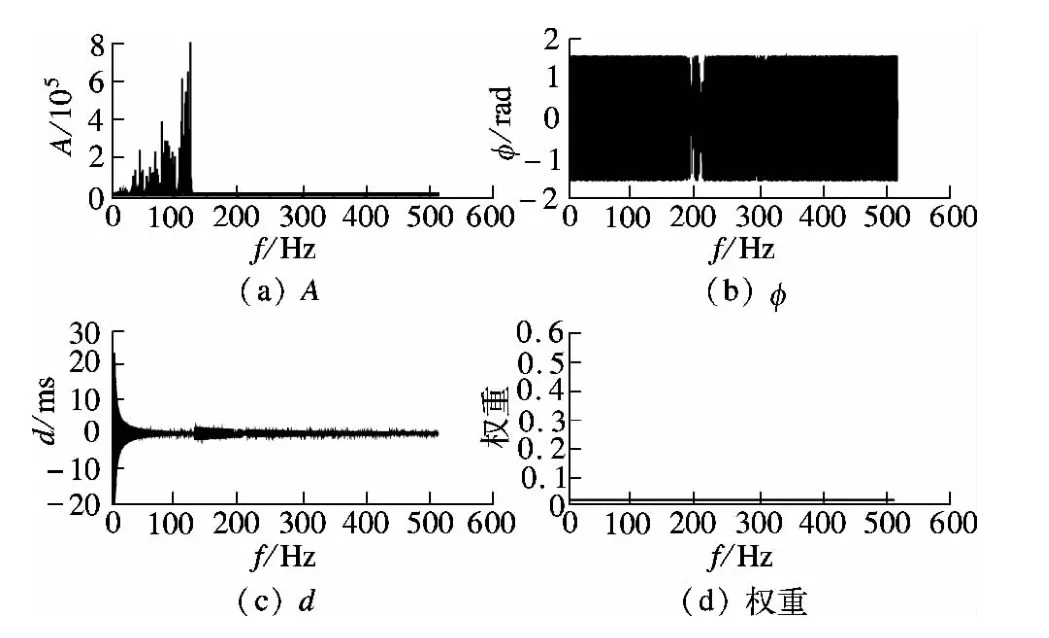
图6 实时混合模拟频域评价方法在各个频率上的指标

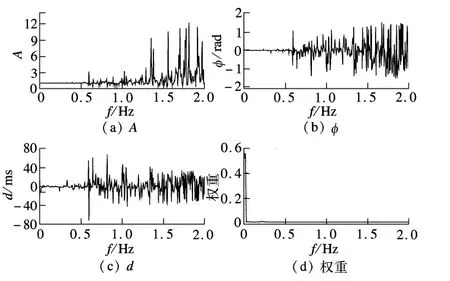
图7 实时混合模拟频域评价方法在低频率上的指标

由图7(a)可发现，在低频区域，幅值A约为1，说明实时混合模拟的幅值误差较小;图7(b)中的相位在0附近，说明实时混合模拟的时滞较小.由图7(c)可见，当频率非常小时，由于虚假时滞的影响，得到的时滞存在较大误差.且由于权重集中于该非常小的范围(见图7(d))，在加权中若将这部分时滞考虑进去会对结果产生较大的影响.经试算，从第4个频率开始加权得到的效果较好，得到的幅值、相位和等效时滞分别为1.007，0.0013 rad和－0.4 ms.这说明实时混合模拟中，测量位移的幅值是计算位移的1.007倍，同时要比计算位移滞后0.4 ms.将式(10)～(12)从第4个频率开始加权，得到综合的幅值A'、相位φ'和等效时滞d'同样是 1.007，0.0013 rad 和－0.4 ms，再次验证了实时混合模拟频域评价方法的意义.

4 结语

本文对实时混合模拟的频域评价方法进行了简要介绍，分别计算了数值模拟和试验中每个频率上的幅值、相位、等效时滞和权重，并与整体的幅值、相位、等效时滞进行对比，证明实时混合模拟的频域评价方法实质上是计算出各个频率的幅值和相位，并按照各频率输入幅值平方的权重进行加权.

各个频率组分在结果中的权重并不相同，低频组分对于结果的影响显著高于高频组分.此外，通过计算每个频率上的等效时滞发现，当频率非常小时，计算得到的等效时滞与时滞的理论值有时会存在显著差异(当权重集中在该低频范围之外时除外).此时可以将前面极低频率组分(如前3个频率)舍弃，从之后的频率开始加权.对于频率的截取，尚需在后续研究中做进一步的分析.

References)

［1］Nakashima M，Kato H，Takaoka E.Development of real-time pseudo dynamic testing ［J］.Earthquake Engineering and Structural Dynamics，1992，21(1):79-92.

［2］Wu B，Bao H，Ou J，et al.Stability and accuracy analysis of central difference method for real-time substructure testing［J］.Earthquake Engineering and Structural Dynamics，2005，34(7):705-718.

［3］Chen C，Ricles J M.Real-time hybrid testing using an unconditionally stable explicit integration algorithm［J］.Earthquake Engineering and Structural Dynamics，2009，38(1):23-44.

［4］Chen C，Ricles J M.Analysis of actuator delay compensation methods for real-time testing ［J］.Engineering Structures，2009，31(11):2643-2655.

［5］Chen C，Ricles J M.Development of direct integration algorithms for structure dynamics using discrete control theory［J］.Journal of Engineering Mechanics，2008，134(8):676-683.

［6］Horiuchi T，Inoue M，Konno T，et al.Real-time hybrid experimental system with actuator delay compensation and its application to a piping system with energy absorber［J］.Earthquake Engineering and Structural Dynamics，1999，28(10):1121-1141.

［7］Chen C.Development and numerical simulation of hybrid effective force testing method［D］.Bethlehem，USA:Department of Civil and Environmental Engineering，Lehigh University，2007.

［8］徐伟杰 实时混合模拟试验的频域评估方法研究［D］.南京:东南大学土木工程学院，2013.

［9］Mosqueda G，Stojadinovic B，Mahin S A.Real-time error monitoring for hybrid simulation.PartⅠ:methodology and experimental verification［J］.Journal of Structural Engineering，2007，133(8):1100-1108.

［10］Mosqueda G，Stojadinovic B，Mahin S A.Real-time error monitoring for hybrid simulation.PartⅡ:structural response modification due to errors［J］.Journal of Structural Engineering，2007，133(8):1109-1117.

［11］Mercan O.Analytical and experimental studies on large scale real-time pseudodynamic testing［D］.Bethlehem，USA:Department of Civil and Environmental Engineering，Lehigh University，2007.

［12］Hessabi R M，Mercan O.Phase and amplitude error indices for error quantification in pseudodynamic testing ［J］.Earthquake Engineering and Structural Dynamics，2012，41(10):1347-1364.

［13］Chen C，Ricles J M，Guo T.Minimizing actuator tracking and energy errors for real-time hybrid simulation through a new adaptive compensation scheme［C］//20th Analysis ＆ Computation Specialty Conference.Chicago，USA，2012:335-345.

［14］王济，胡晓.MATLAB在振动信号处理中的应用［M］.北京:中国水利水电出版社，知识产权出版社，2006.

［15］Wallace M I，Sieber J，Neild S A，et al.Stability analysis of real-time dynamic substructuring using delay differential equation models ［J］.Earthquake Engineering and Structural Dynamics，2005，34(15):1817-1832.

［16］Wen Y K.Equivalent linearization for hysteretic systems under random excitation［J］.Journal of Applied Mechanics，1980，47(1):150-154.