钢筋锈蚀引起混凝土结构锈裂综述

赵羽习

(浙江大学结构工程研究所，杭州 310000)

在影响混凝土结构耐久性的众多因素中，钢筋锈蚀引起的混凝土结构开裂被认为是钢筋混凝土结构耐久性失效的最主要原因之一.

混凝土结构在服役过程中，环境中的有害介质侵入到混凝土内部，破坏钢筋表面的钝化膜，引发钢筋锈蚀和铁锈膨胀，锈蚀产物的体积是原有体积的2～4倍，其体积膨胀行为受到周围混凝土的限制，在钢筋/混凝土界面上产生压力，即钢筋锈胀力.随着钢筋锈蚀量的增加，逐渐增大的钢筋锈胀力将导致混凝土保护层受拉而开裂.锈胀裂缝首先在钢筋周边的混凝土内界面产生，由内而外逐渐扩展;当锈胀裂缝贯通混凝土保护层时，环境中的有害介质经锈胀裂缝直接侵入混凝土内部，接触到钢筋，钢筋锈蚀速度大大加快，进一步加剧混凝土锈胀裂缝的扩展，甚至导致混凝土保护层剥落，严重影响混凝土结构的耐久性.

混凝土保护层锈裂过程对混凝土结构的性能劣化规律和使用寿命有着重要的影响，众多国内外学者开展了相关研究工作，取得了一系列研究成果.本文从试验研究、理论分析和数值模拟3个方面对钢筋锈蚀引起混凝土结构锈胀开裂的研究成果进行综述，也对该领域尚待深入研究的内容进行讨论.

1 试验研究

针对混凝土保护层锈胀开裂的试验研究主要集中在2个方面:①从钢筋脱钝开始，锈蚀到混凝土保护层表面开裂的时间或混凝土表面开裂时刻的钢筋锈蚀量;②开裂以后混凝土表面裂缝宽度的发展规律.在试验研究的基础上，许多学者建立了表面开裂时间以及裂缝宽度的经验模型.

1.1 保护层表面锈裂的临界锈蚀量

一旦混凝土表面出现裂缝，外界溶液便能通过裂缝渗入混凝土内部，直接接触到钢筋表面，从而加速钢筋的锈蚀，因此，混凝土表面开裂是锈裂过程中非常重要的时刻.很多学者对表面开裂时刻的钢筋锈蚀量或开裂时间进行了试验研究.

Andrade等［1］对钢筋位置、钢筋直径和保护层厚度不同的4组试块进行加速锈蚀试验，施加的锈蚀电流有10和100 μA/cm2两种.假定钢筋均匀锈蚀，根据法拉第定律，由通电电流和通电时间来计算任一时刻的钢筋锈蚀深度，计算经验公式为:

式中，δ为钢筋锈蚀深度，μm;icorr为锈蚀电流密度，μA/cm2;t为通电时间，年.试验发现，出现第1条表面可见裂缝(裂缝宽度为0.05～0.10 mm)的钢筋锈蚀深度一般为10～20 μm.

Alonso 等［2］的试验与 Andrade 等［1］的试验类似.施加的锈蚀电流有 3，10，100 μA/cm2三种.通过分析试验结果发现，出现第1条表面可见裂缝时刻的钢筋锈蚀深度δsurface与C/d呈线性关系，即

式中，C为混凝土保护层厚度，mm;d为钢筋直径，mm.

Rodriguez等［3］同样进行了基于钢筋混凝土梁的加速锈蚀试验，得到了表面开裂时刻钢筋锈蚀深度计算的经验公式，即

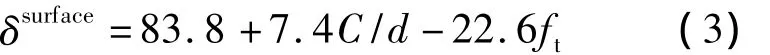
式中，ft为混凝土的抗拉强度，MPa.

Webster等［4］建立的经验公式较为简单，认为表面开裂时刻钢筋锈蚀深度与混凝土保护层厚度线性相关，即

张伟平［5］对配置4根纵向钢筋的混凝土棱柱体进行了研究，建立了临界锈蚀深度的经验公式，即

式中，fc为混凝土的抗压强度，MPa.

在Oh等［6］的研究中，通过应变值来判断开裂情况，认为监测到的应变值达到混凝土开裂应变时，保护层表面即出现初始裂缝，由此建立了保护层表面开裂时刻钢筋锈蚀率ρsurface与保护层厚度C之间的关系，即

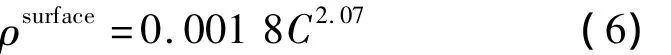
另外，Liu等［7-9］试验研究了钢筋锈蚀速率、混凝土保护层厚度、钢筋间距、钢筋直径、混凝土质量等因素对混凝土表面开裂时间的影响.

图1 表面开裂时钢筋锈蚀深度预测值与试验值对比

为了分析各种混凝土保护层表面开裂的经验公式的适用性，采用文献［2-6］的经验公式，分别对文献［1-9］试验测得的临界钢筋锈蚀深度进行预测.预测结果与试验测试值的对比图见图1(a).由于经验公式由试验数据拟合得来，各学者的经验公式对自己的试验必然有较好的预测性.因此，为了更清楚地表示经验公式预测的广泛适用性，图1只绘出了各学者的经验公式对其他学者试验的预测结果，而并未对自身的试验结果进行预测.图1(b)为图1(a)的局部放大图.图中直线为准确预测线，数据点离该直线越近，预测结果越准确.由图可知，这些经验公式预测的钢筋锈蚀深度与试验值都存在较大误差.特别是Oh的公式预测结果，远远大于实际的试验值.分析其原因在于，混凝土结构的锈裂过程受多种因素影响，而经验公式无法全面地考虑众多影响因素，往往只与其中1个或2个因素相关，从而导致了从某一试验中得到的经验公式不适用于其他锈裂试验的情况.由此可见，采用经验公式对锈裂过程进行预测，存在较大的局限性.

1.2 保护层表面裂缝开展

由于混凝土保护层表面的裂缝宽度能够直观地反映锈裂的情况，对其进行观测也非常简便.因此，在大部分锈胀开裂试验中，都对表面裂宽的开展进行了研究.

Alonso 等［2］通过试验发现，15 ～ 50 μm 的钢筋锈蚀深度能使表面产生宽约0.05～0.10 mm的裂缝;而使裂宽达到0.20～0.30 mm需要的钢筋锈蚀深度为50～200 μm.

Rodriguez等［3］通过试验，建立了表面裂缝宽度Ws的经验公式，即

式中，β的取值取决于钢筋在混凝土梁中的位置.对于顶部钢筋，β=0.0100;对于底部钢筋，β=0.0125.

Vidal等［10］对2根在氯盐环境下分别暴露14和17年的3 m长钢筋混凝土梁进行了研究.通过失重法测量计算钢筋不同位置处的锈蚀情况，并测量相应位置处的表面裂缝宽度，建立了裂缝宽度和钢筋锈蚀截面损失面积的关系，即

式中，ΔAs为钢筋截面损失面积，mm2;ΔAs0为混凝土表面出现第1条裂缝时的钢筋截面损失面积.ΔAs和ΔAs0可分别由下式计算:

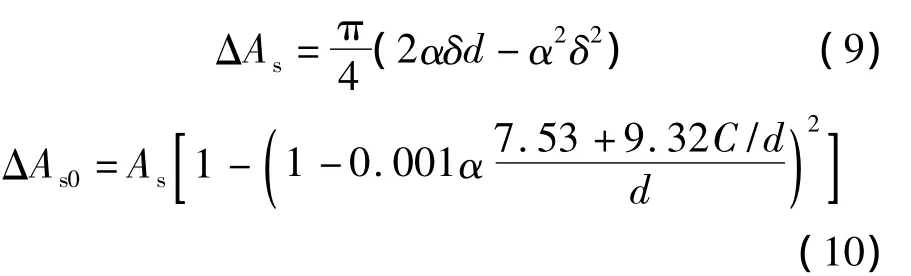
式中，α为不均匀锈蚀系数，对于均匀锈蚀的情况，α=2;As为钢筋的初始横截面面积.式(10)中出现了式(2)的表达式，这是因为在预测表面开裂时刻的钢筋锈蚀量时，Vidal采用了Alonso的研究结果.

延续 Vidal等［10］的研究，Zhang 等［11］对 2 根在氯盐环境中放置14和23年的梁进行了观测研究.假定钢筋为均匀锈蚀，建立了钢筋平均截面损失面积ΔAs0与裂缝宽度Ws之间的关系，即

王深［12］对钢筋直径和保护层厚度不同的棱柱体试件进行了研究，建立了钢筋锈蚀深度与裂缝宽度之间的关系，即

Vu等［9］引入了混凝土品质 C/(wc)这一概念，即混凝土保护层厚度与水灰比的比值，其中wc为水灰比.通过试验得出，从保护层表面开裂至裂缝发展到一定宽度所需的时间t与C/(wc)存在非线性关系，即

式中，A，B为系数，对于不同的裂缝宽度，有不同的取值.文献［9］给出了裂缝宽度为 0.3，0.5，1.0 mm时分别对应的A和B的取值.

另外，对于从保护层开裂至裂缝开展到一定宽度所需的时间，Vu等［9］还建立了其在加速锈蚀环境中与在实际工程结构中锈蚀时间的关系，即

式中，t(exp)和icorr(exp)分别为加速锈蚀试验的锈蚀时间和锈蚀电流;t(real)和icorr(real)分别为实际工程结构构件的锈蚀时间和锈蚀电流;kR为荷载修正系数，可由下式计算:

Mullard等［13］通过对钢筋混凝土板的加速锈蚀试验，建立了保护层表面开裂后的锈蚀时间与表面裂缝宽度之间的关系，即

式中，kc为限制系数，表示周围混凝土对裂缝开展的限制程度.对于位于中间的钢筋，kc=1;而对于外侧的钢筋，kc＞1.式(16)适用于 0.1≤C/(dft)≤1，w≤1.0 mm 的情况.

夏晋［14］的模型有别于以往的线性模型，认为锈胀裂缝宽度与钢筋锈蚀率呈对数关系，即

式中，K为系数，针对不同类型的试件，文献［14］给出了不同的回归值.

下面以文献［9］试验中的某一试件为例，讨论各经验公式的适用性.该试件的保护层厚度为25 mm，钢筋直径为16 mm，混凝土抗压强度为20 MPa，抗拉强度为3.06 MPa，实际电流密度为140 μA/cm2，在试验时间为95.5 h时观察到表面裂缝，折算成钢筋锈蚀深度即为17.7 μm.分别用文献［3，10-13］中的经验公式来预测裂缝开展的情况.图2中给出了各经验公式预测的混凝土保护层表面裂缝宽度与钢筋锈蚀深度的关系.图中，虚线表示文献［9］中测得的裂缝宽度的真实变化情况.由图可知，对达到某一裂缝宽度的钢筋锈蚀深度进行预测时，利用文献［11，13］中经验公式得到的预测结果明显偏大，而基于文献［3，10］中经验公式得到的预测结果则大大偏小.只有根据文献［12］中经验公式得到的预测结果与真实情况相对接近.但这仅是针对本算例的情况，若将模型用于其他试验数据的预测，可能会发生预测出现偏差的情况.由此可见，通过试验建立经验公式对混凝土表面锈裂宽度进行预测，其普遍适用性仍存在问题.

图2 不同模型对表面裂缝宽度的预测结果

1.3 经验公式的适用性讨论

各学者基于试验数据拟合提出的混凝土表面锈裂时刻和混凝土表面锈胀裂缝宽度预测经验公式，一般仅与自己的试验数据有着较好的预测准确性，对其他试验数据的预测结果往往并不理想.各个经验公式的普遍适用性仍存在问题.这是由于混凝土结构的锈裂过程受混凝土材料、保护层厚度、钢筋直径和位置、环境等多种因素的影响，而各经验公式中的钢筋锈蚀深度或裂缝宽度预测往往只与其中主要的1个或2个因素相关，并不能全面、综合地考虑所有影响因素.另一个主要原因是，各学者采用的试验方法不尽相同.例如，对于混凝土内钢筋加速锈蚀方法，有的学者采用干湿循环法，有的学者则采用通电加速钢筋锈蚀;即便都采用通电加速方法，不同学者试验过程中设置的通电电流密度也不一定相同，这也是导致不同试验测试结果存在差异的原因之一.此外，各项试验中，混凝土表面锈裂时刻的观测方法也有所不同，大多数试验采用人工观测混凝土表面锈裂，这样可能导致观测时间滞后于实际锈裂时间，从而使得试验数据偏大.

可见，虽然采用试验观测混凝土锈裂过程是直观、易行、有效的研究手段，但是仅根据有限试验数据拟合得到的经验公式对锈裂过程进行预测，还存在较大的局限性.针对混凝土锈裂试验，如能采用统一的试验方法(包括试件、钢筋锈蚀加速方法、锈裂观测方法等)测试混凝土锈裂过程中的关键数据，得到的经验公式会有更为广泛的适用性和应用价值.

2 理论模型

2.1 混凝土锈裂三阶段理论

对于混凝土结构的锈胀开裂过程，锈裂三阶段理论［7］得到大部分学者的认可，即从混凝土构件钢筋脱钝到混凝土保护层开裂，大致要经历如下3个阶段(见图3):

1)铁锈自由膨胀阶段.钢筋脱钝开始锈蚀后，产生的铁锈首先填入毛细孔和空隙中.在铁锈填满空隙之前，不会对外围混凝土产生钢筋锈胀力.

2)混凝土保护层受拉应力阶段.当铁锈填满钢筋与混凝土交界面毛细孔后，钢筋进一步锈蚀产生的铁锈将对外围混凝土产生钢筋锈胀力，从而使得混凝土保护层受到拉应力，且该拉应力随着钢筋锈蚀的发展而增大.

3)混凝土保护层开裂阶段.当钢筋锈蚀深度达到一定值时，混凝土保护层在钢筋表面附近首先出现裂缝，裂缝随着钢筋锈蚀的发展逐渐开展到混凝土表面.此阶段产生的铁锈使得混凝土保护层中的裂缝不断开展，同时也会逐渐填充到开展的裂缝中.

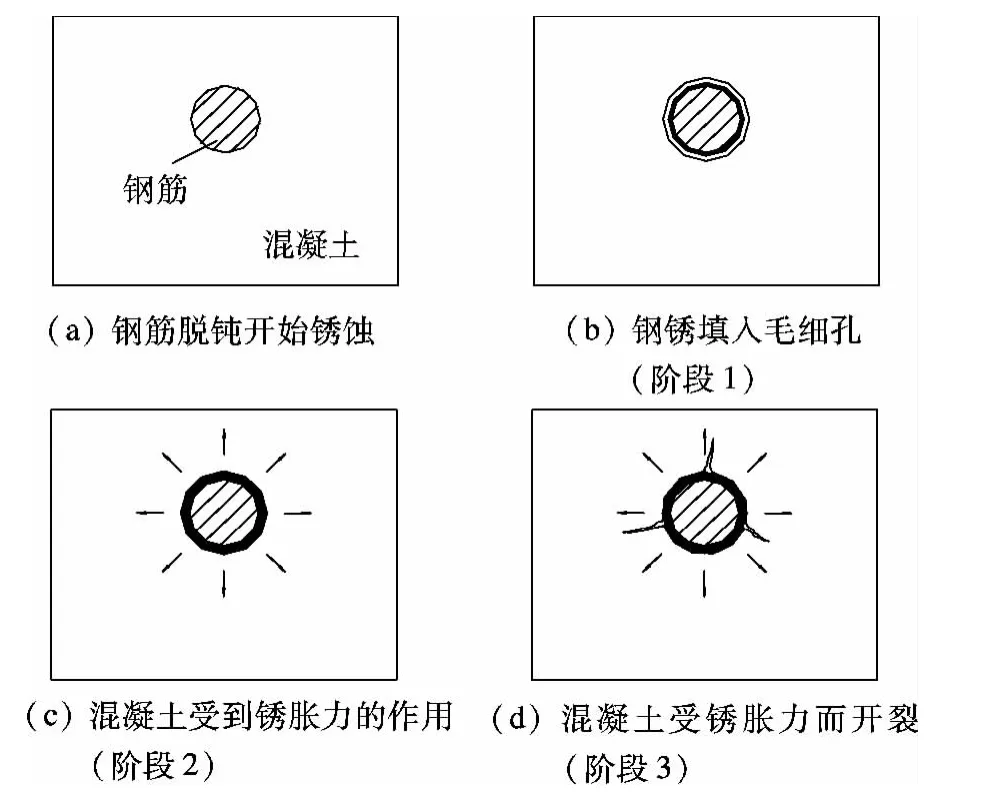
图3 混凝土结构锈裂三阶段［15］

由三阶段理论可知，混凝土胀裂时刻的钢筋锈蚀深度由以下3个部分组成:① 钢筋锈蚀深度δpore，即铁锈自由膨胀阶段产生的锈蚀深度.② 钢筋锈蚀深度δstress.锈蚀产物使钢筋/混凝土界面产生钢筋锈胀力，导致混凝土保护层受拉开裂，这一现象产生于阶段2和阶段3.③ 钢筋锈蚀深度δcrack.锈蚀产物填充到裂缝中，这一现象产生于阶段3.混凝土胀裂时刻的钢筋锈蚀深度为

下面主要介绍混凝土表面锈裂预测理论模型方面的研究进展及尚存在的问题.

2.2 铁锈自由膨胀阶段

2.2.1 铁锈填充区域的假设

Liu等［7］提出三阶段理论时，假设在钢筋混凝土界面存在空隙区，则阶段1中铁锈填充量为

式中，ρrust为铁锈的密度;D为钢筋直径;d0为假设的空隙区厚度.孔隙的体积与钢筋表面积、水灰比、水化和硬化程度直接相关，需要通过试验定量研究低、中、高强度混凝土中的孔隙体积.在文献［7］对试验结果的模型验证中，假设d0=12.5 μm.

笔者［15］曾建立了模拟混凝土构件锈裂过程的模型，对于阶段1中铁锈的填充量，近似认为铁锈充满钢筋周围混凝土孔隙，估算出钢筋与混凝土交界面混凝土孔隙的体积，并折算为钢筋外围的均匀锈层厚度，即

式中，Pvp为毛细孔占水泥石的体积百分数，且Pvp=0% ～40%;dp为毛细孔的平均孔径，且dp=1～50 μm.δp的波动范围为 1 ～ 20 μm，随混凝土等级、施工和养护条件等而发生变化，对应的钢筋锈蚀深度还与铁锈膨胀率有关.缺少混凝土材料条件时，δp取均值 10 μm.

陆春华等［16］建立的锈裂模型中考虑了锈蚀产物对混凝土孔隙的填充.对于铁锈在混凝土孔隙中的填充，假定钢筋/混凝土界面的孔隙区均匀分布且厚度为 δ0，并将 δ0取值为 15 μm.

在文献［17］建立的混凝土保护层锈胀开裂模型中，计算铁锈自由膨胀阶段的锈层厚度时，将混凝土中的孔隙区域厚度取为100 μm，毛细孔占水泥石的体积百分比取为20%，则折算后的铁锈填充区域厚度为20 μm.

2.2.2 铁锈填充区域的试验研究

Michel等［18］提出了铁锈填充区域(corrosion accommodating region，CAR)的概念，用以描述钢筋周围混凝土保护层中被铁锈填充的区域，并采用X射线测试技术，观测了锈蚀产物随时间的变化过程和分布情况以及锈胀裂缝的产生和发展过程.试验结果验证了铁锈在水泥砂浆中填充现象的存在，并且发现，随着时间的增长，锈蚀产物的填充深度逐渐增加，在第1条锈胀裂缝产生时，铁锈填充区域CAR的范围为0.09～0.18 mm，但随着通电的继续进行，CAR范围继续增加至约0.60 mm.在第2条裂缝开展后，铁锈不再侵入砂浆中，而是在钢筋-砂浆界面积累，对外产生挤压，使砂浆显著变形.

Caré等［19］利用光学显微镜和扫描电镜，结合能谱分析方法，研究了通电加速锈蚀条件下的锈层分布，并通过数字摄像系统记录下锈裂过程，对钢筋/砂浆界面的位移场变化进行观测.在通电的不同阶段将试块切片、观察，研究结果验证了填充区域的存在，并指出填充区域并未存在于整个钢筋周围，但没有对填充区域进行定量测量.

Wong 等［20］提出用 CP(corrosion-filled paste)来表示混凝土保护层中的铁锈填充区域.试验采用干湿循环法对试件进行氯盐侵蚀环境下的加速锈蚀，对产生锈胀裂缝的试块进行切割处理，得到观测试样.通过光学显微镜、背散射电子显像和能量色散X射线显微分析等图像分析方法，研究了试样中锈蚀产物的分布情况.扫描电镜结果证实了铁锈填充区域CP的存在，且铁锈填充区域主要分布在靠近保护层一侧的20% ～25%圆周处，即钢筋截面锈蚀程度较严重的一侧.对BSE图像进行定量测量分析发现，对于不同锈蚀程度的试样，铁锈填充区域的深度差别不大.随着钢筋锈蚀量的增加，锈层(corrosion layer，CL)的面积增大，铁锈填充区域CP的平均厚度大约为100～200 μm(见图4).

图4 CP，CL的平均厚度随钢筋锈蚀率的变化关系［20］

笔者［21］利用 SEM和EDS法，对直流通电加速钢筋锈蚀的混凝土试件进行了研究，观测到铁锈填充区的存在，但未做深入定量研究.笔者近期对干湿循环条件下锈蚀钢筋混凝土试样的进一步观测发现，在混凝土锈胀开裂过程中，钢筋锈蚀产物向混凝土中的填充与其在钢筋/混凝土界面处的积累是同时进行的(见图5)［22］.这与锈裂三阶段理论的假设不同，铁锈自由膨胀阶段并不存在.

2.2.3 分析讨论

图5 铁锈填充区域平均厚度随锈层厚度的变化［22］

根据已有的试验观测情况发现，以往研究中对铁锈填充区域的假设缺乏依据.笔者认为，铁锈填充区域的研究应注重试验研究和实测数据的积累.将与混凝土构件锈裂过程中铁锈填充行为有关的试验研究结果汇总于表1中.由表可知，目前对于混凝土构件锈裂过程中铁锈填充行为的研究并不多，尤其缺少定量的研究成果.此外，研究多基于直流通电的方法，对试件进行加速锈蚀，在这种条件下，钢筋锈蚀环境与自然条件下相差较多.这是因为:一方面，锈蚀速率不同可能会导致裂缝中的铁锈填充行为有所区别，试验结果无法完全体现真实的锈裂过程中铁锈对裂缝的填充情况;另一方面，虽然研究成果可以对锈裂过程中的铁锈填充行为进行验证，但是，过快的钢筋锈蚀速率使试验的定量研究成果可能会与真实情况有所区别.

表1 铁锈填充区域的试验研究

根据笔者最新的研究成果［22］发现，混凝土中的铁锈填充混凝土孔隙过程和钢筋/混凝土界面的锈层积累是同时进行的.因此，要建立准确的混凝土锈裂模型，应对这种现象加以考虑.目前，对于锈裂过程中钢筋锈蚀产物的填充行为，尚需要进行更深入的试验研究;铁锈填充区域和锈层积累之间的定量关系，亦需要投入更多的关注，以得到对于建立锈裂模型更有参考价值的定量研究成果.

2.3 混凝土受拉应力开裂阶段的锈裂模型

2.3.1 混凝土锈裂计算模型

Bazan［23］分析了保护层开裂产生的剥落和分层2种破坏现象.根据钢筋锈蚀过程中各反应物质的质量守恒、Fick第一扩散定律、Maxwell静电方程及化学反应速率方程等，建立了一组微分方程，针对海洋混凝土结构的特点，给出了钢筋锈蚀的理论物理模型，提出了保护层锈胀开裂时间计算的简化方法.

在基本模型建立方面，学者们通常以钢筋和周围混凝土作为研究对象.假定钢筋锈蚀是均匀的，产生均匀的锈蚀膨胀应力，将混凝土结构简化为受均匀内压作用的单层或双层厚壁圆筒，圆筒内径为钢筋半径R，裂缝前端半径为Rc(见图6).

图6 锈胀开裂分析模型

Liu等［7］假设混凝土保护层破坏时，各点的环向应力同时达到混凝土的抗拉强度，忽略混凝土开裂后的剩余刚度，由平衡关系直接计算此时的钢筋锈胀力，最终得到保护层表面开裂的时间.

郑建军等［24］考虑混凝土开裂后的软化特性，将开裂的混凝土柱体划分成开裂柱体和未开裂柱体2个部分.未开裂柱体仍然是各向同性弹性体;开裂柱体的环向刚度由于混凝土开裂而下降.引入弥散裂缝，将径向裂缝等效分布在混凝土柱体的各个方向，把开裂混凝土柱体看成是正交各向异性弹性体，由此进行混凝土锈蚀损伤全过程分析，认为混凝土柱体内半径处的径向位移等于铁锈层的厚度，开裂处的环向应力等于混凝土抗拉强度.最后，求得混凝土保护层完全开裂的时间.

笔者［25］分别考虑混凝土保护层和铁锈层的受力性能，对混凝土和铁锈采用弹性理论进行分析(见图7).混凝土与铁锈层之间存在变形协调关系，即式中，R1为钢筋锈蚀自由膨胀后的名义半径;δcon为外围混凝土受钢筋锈胀力作用发生的变形;δrust为钢筋锈蚀自由膨胀后d1受钢筋锈胀力作用产生的变形.根据式(21)可计算出钢筋锈胀力q，并由计算出保护层开裂时刻的钢筋锈胀力，即可解得混凝土保护层表面开裂时刻的钢筋锈蚀率.

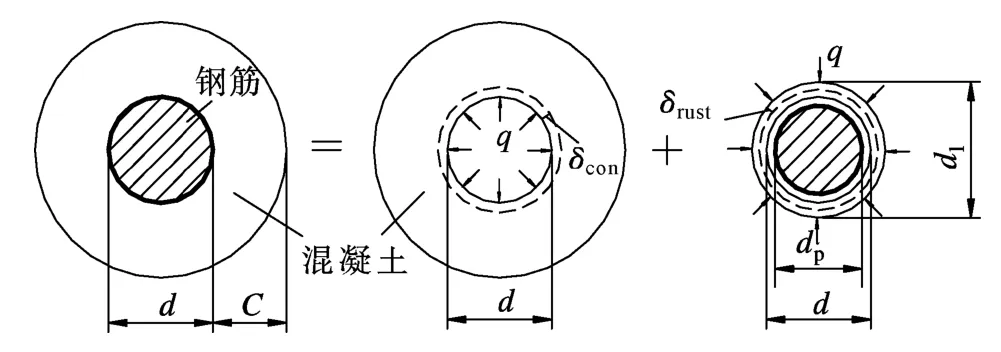
图7 钢筋混凝土构件受钢筋锈胀力变形图［25］

笔者在后续的研究中，利用损伤力学和弹性力学的理论，引入损伤变量这一概念，考虑混凝土的损伤情况，建立了部分开裂混凝土保护层的锈胀开裂模型［26］.而后，进一步发展该锈裂模型，使其可以预测混凝土表面锈裂宽度［27］.

Bhargava等［28-29］假定钢筋锈蚀产物的弹性模量、泊松比与钢筋相同，将钢筋和锈蚀产物看成一个整体，并假定其弹性模量和泊松比分别为210 GPa和0.3，由此建立混凝土开裂时间分析模型.

Pantazopoulou等［30］将开裂混凝土看成各向异性材料，根据混凝土开裂后的材料特性，利用有限元软件对混凝土的径向位移u进行求解.

Chernin等［31］同样将混凝土保护层分为内裂和未裂2个部分，假定内部开裂柱体的环向弹性模量随半径变化.陆春华等［16，32-33］也采用了弹性力学理论，对均匀锈蚀条件下钢筋混凝土结构锈胀开裂的过程进行研究.

王海龙等［34］考虑混凝土界面中的原始裂纹与缺陷、裂纹在钢筋锈蚀膨胀作用下的起裂、扩展情况，利用断裂力学和弹性力学，得到了混凝土保护层开裂时刻钢筋锈胀力与均匀锈蚀率的理论预测模型.混凝土保护层发生开裂的临界锈胀力可表示为

式中，R0为钢筋中心到锈胀后混凝土与锈胀物之间界面的距离;F为与裂缝长度、R0和R1有关的函数为界面裂纹发展的最大长度;KIC为混凝土的断裂韧度.

在文献［24］中的锈裂模型基础上，Li等［35］认为混凝土为准脆性材料，引入断裂力学来分析混凝土中的应力和应变.此模型不仅可以计算保护层表面开裂前的情况，还可以得到保护层表面裂缝宽度与钢筋锈蚀深度之间的关系.分析结果表明，在混凝土保护层临界开裂时刻，裂缝瞬间由0开展到一定宽度，钢筋锈胀力也有大幅度的减小，这是由于混凝土的脆性所致.

王显利等［36］依据断裂韧度和最大荷载的关系，确定临界锈胀力，得到了钢筋混凝土结构保护层临界锈胀力预测模型.

罗晓辉等［37］利用损伤力学的方法，假定钢筋产生均匀锈蚀时锈蚀层膨胀效应与温度膨胀效应具有相似性，采用锈蚀温度环模拟锈蚀层膨胀效应;假定钢筋锈蚀所产生的膨胀应力导致了混凝土中粗骨料与砂浆的界面应力，采用能量释放率描述界面裂纹开展的阻力梯度，从而得到粗骨料与砂浆界面效应的细观断裂性能，建立了混凝土保护层的损伤模型.与氯离子侵蚀条件下的钢筋锈蚀预测模型相结合，建立了钢筋保护层损伤的时间序列分析方法，对开裂前混凝土中的损伤过程进行了分析.

Li等［38］假定距离钢筋无穷远处的应力是均匀的，使用Muskhelishvili复变函数法，对混凝土结构锈裂过程进行了模拟.

Malumbela等［39］认识到混凝土内部钢筋锈蚀的不均匀性，建立了不均匀锈蚀情况下钢筋锈蚀程度与混凝土表面应变之间的关系模型.模型中假定钢筋锈蚀后剩余截面形状为椭圆形，并假设在变化的内部锈胀应力作用下，保护层混凝土的行为与钢筋的锈蚀程度有关，从而得到紧靠锈蚀产物的混凝土的理论最大径向膨胀位移以及对应的混凝土表面最大横向应变.

冯瑞等［40］假定锈胀力分布规律与钢筋锈蚀层分布规律是一致的，将锈蚀层的轮廓线取为椭圆曲线，利用弹性理论建立了非均匀锈蚀情况下锈胀力的表达式.

2.3.2 模型比较与讨论

2.3.1 节中各模型的对比见表2.文献中的模型均可对混凝土锈裂行为进行预测，部分模型的预测结果与试验测试结果具有较好的吻合度.但是，从表中可以看到，各模型也存在一定的不足，在对混凝土开裂后剩余强度的考虑、钢筋锈蚀产物的力学性能对锈裂过程的影响、铁锈填充裂缝的情况等方面，各模型都难以做到全面、完善的考虑.

混凝土锈裂计算模型的复杂性，首先源于材料的复杂性.混凝土锈裂力学分析涉及到混凝土、铁锈和钢筋3种材料.混凝土是多种材料复合而成的准脆性材料，简单采用弹性理论分析混凝土材料的开裂过程，必然存在不合理性.因此，后期的混凝土锈裂模型引入断裂力学、损伤力学等方法，可以较好地分析混凝土保护层锈裂力学过程.铁锈的产生不但源于混凝土保护层锈裂，其本身也全程参与了混凝土锈裂力学过程.然而，在很多研究工作中，由于铁锈本身的复杂性，对混凝土锈裂力学过程进行分析时，或不考虑铁锈，或采用一些假设的参数，这在一定程度上影响了混凝土锈裂分析的准确性与合理性.笔者曾进行过一系列试验研究，测试分析钢筋混凝土内部锈层的参数，如铁锈模量、铁锈膨胀率等，可供混凝土锈裂研究参考［41-42］.

应该看到，国内外学者已经对混凝土受拉应力开裂阶段的锈裂模型开展了较多研究，但计算模型一般假定钢筋表面的锈蚀与锈胀力沿圆周均匀分布，其原因在于:①在建立锈胀模型时简化计算;②目前的研究成果中鲜见描述非均匀锈层在钢筋周围形成和发展的试验与实测数据.而事实上，实际工程中钢筋均匀锈蚀的现象并不多见，具有普遍性的情况是侵蚀环境下导致的钢筋非均匀锈蚀.钢筋的均匀与非均匀锈蚀引起的混凝土锈胀开裂情况是有所不同的;混凝土结构的锈裂过程不仅与钢筋的锈蚀程度有关，与钢筋表面锈蚀分布情况也是密切相关的.因此，在后续的混凝土锈裂理论模型中，应该更多地研究更符合实际情况的钢筋非均匀锈蚀引起混凝土开裂的情况.

表2 混凝土锈裂模型汇总

混凝土结构是在环境与荷载共同作用下服役的，但是目前的锈裂计算理论模型往往关注环境(钢筋锈蚀)引起混凝土开裂的行为，尚未能很好地将荷载作用考虑到混凝土锈裂模型中.因此，在后续混凝土锈裂理论模型的建立中，应注重荷载与环境耦合作用下的裂缝开展情况，以使得锈裂预测模型更符合实际混凝土工程状况.

还需指出的是，箍筋锈蚀也会引起混凝土保护层锈裂.很多实际工程中，由于保护层很薄，箍筋锈胀裂缝往往比纵筋锈胀裂缝出现得更早.箍筋对混凝土锈裂的影响是复杂的:一方面，箍筋限制纵筋锈胀裂缝的发展，这是有益的作用;另一方面，箍筋与纵筋搭接处的钢筋锈蚀尤其严重，更容易引起锈裂现象，而箍筋本身的锈蚀也会引起混凝土保护层的锈裂.因此，箍筋锈蚀引起的混凝土保护层开裂以及箍筋对纵筋锈蚀引起混凝土开裂的影响，迄待更多的研究.

2.4 锈胀裂缝中铁锈的填充

2.4.1 假设条件

部分学者［24，28-29，35］在理论模型计算中不考虑填充到裂缝中锈蚀产物的影响.另一些研究人员则基于假设提出了一些近似计算方法.例如，Pantazopoulou等［30］认为裂缝形状为三角形，裂缝在开展过程中，铁锈完全填入到裂缝之中.笔者［25］也曾假设裂缝面积按三角形考虑，铁锈填满裂缝，并且认为裂缝在初期是稳定开展的，但是当裂缝长度超过某个值e后，裂缝会迅速开展至表面，因而铁锈不会填充到阈值e之后产生的裂缝中.陆春华等［16］认为，对于长期自然锈蚀，锈蚀产物会进入并填满裂缝，而对于短期加速锈蚀，由于锈蚀产物生成速度快，锈胀力快速增大，在锈蚀产物没有完全进入裂缝之前，混凝土保护层就可能完全锈胀开裂，因此引入了锈蚀产物进入裂缝的锈蚀深度修正系数，对不同锈蚀情况下的锈蚀深度进行修正.

2.4.2 试验研究

Michel等［18］采用X射线测试技术观测了锈蚀产物随时间的变化过程和分布情况，采取直流通电加速锈蚀的方法使混凝土试块锈胀开裂.试验结果表明，在通电锈蚀过程中铁锈并未填入锈胀裂缝中.

Wong等［20］对锈胀裂缝中的铁锈填充情况进行了观察，发现铁锈填充情况比较复杂，认为铁锈在裂缝中的填充可能与距钢筋的距离和铁锈宽度等都有关系，对于铁锈是否会在裂缝中有所填充仍未得出确定的结论.

笔者［21］利用直流通电的方法，对圆柱形试块进行加速锈蚀，采用SEM和EDS，研究了锈胀裂缝中的铁锈填充情况.研究结果表明，通电锈蚀情况下，铁锈不会填充到裂缝之中.在后续研究［22］中，通过对干湿循环加速锈蚀的长方体试块进行电镜扫描和能谱分析发现，在混凝土表面锈裂前，钢筋的锈蚀产物不会填入锈胀裂缝中，只有当锈胀裂缝贯穿混凝土保护层后，才会有部分锈蚀产物随溶液流出，并附着到裂缝的边缘.

2.4.3 分析讨论

将与混凝土构件锈裂过程中铁锈填充裂缝行为有关的研究成果汇总于表3中.从目前已经取得的试验研究成果来看，在混凝土锈胀裂缝发展到混凝土表面前，铁锈是不会填充到锈胀裂缝中的.这就对原有的混凝土表面锈裂三阶段理论提出了质疑.在混凝土表面锈裂时刻预测模型中，无需考虑填入锈胀裂缝中的铁锈量δcrack.混凝土表面锈裂三阶段模型可以修正为二阶段模型.

表3 铁锈填充行为研究汇总

2.5 混凝土锈裂二阶段模型

根据上述讨论可知，锈蚀产物在混凝土孔隙中的填充和钢筋/混凝土界面处的积累是同时进行的，并且铁锈不会对混凝土结构的锈胀裂缝进行填充.因此，钢筋混凝土结构的锈裂过程可以分为如下2个阶段:

1)阶段1 该阶段从钢筋脱钝至锈蚀填充区域CP层厚度TCP达到稳定值为止.钢筋脱钝，锈裂过程进入第1阶段(见图8(a)).在此阶段中，钢筋锈蚀产生的锈蚀产物部分在钢筋/混凝土界面处积累形成锈层，其厚度记为TCL;其余部分填充于混凝土孔隙中，形成铁锈填充区域，其厚度记为TCP(见图8(b)).随着钢筋锈蚀的进行，TCP不断增大，增加到一定值后不再继续增大，即达到最大值，第1阶段结束(见图8(c)).该阶段的钢筋锈蚀量记为δ1.

2)阶段2 CP层厚度停止增长，CL层厚度继续增加，直到混凝土表面锈裂.这一阶段中，钢筋锈蚀产生的锈蚀产物全部在钢筋/混凝土界面处积累，使TCL继续增长，直到混凝土表面锈裂，该阶段结束(见图8(d)).该阶段的钢筋锈蚀量记为δ2.

图8 混凝土锈裂二阶段理论示意图

因此，混凝土表面锈裂时刻钢筋的总锈蚀深度δ可用二阶段模型表示为

3 数值模拟

建立于大部分实际混凝土工程中的非均匀钢筋锈蚀理论模型，是一项具有挑战性的工作.至今，仍未见能被广泛接受的非均匀钢筋锈胀力作用下的混凝土锈裂模型.而有限元方法则是解决非均匀钢筋锈蚀情况的有利工具.

3.1 研究现状

Dagher等［43］采用有限元方法，对钢筋锈蚀产物体积膨胀引起混凝土结构锈裂损伤的过程进行模拟，并采用弥散裂缝和节点位移方法加载，模拟各种钢筋锈蚀.该数值模型可以很好地帮助理解混凝土锈裂过程.

Molina等［44］建立了有限元模型，对4个混凝土试件的锈裂试验过程进行模拟.该模型采用弥散裂缝模拟混凝土裂缝开展行为，还采用改变锈蚀界面钢筋弹性模量的方法对铁锈也加以考虑.该有限元模型和试验结果较为符合.此外，还利用该模型讨论了混凝土锈裂的影响因素.

张伟平［5］采用温度膨胀环模拟锈蚀产物，对混凝土中钢筋的锈胀损伤机理进行有限元分析，根据分析结果提出了混凝土保护层锈胀开裂时刻的钢筋截面锈蚀率模型.

Zhou等［45］采用有限元方法，分析了钢筋锈蚀引起混凝土桥面板的锈裂行为，并利用该有限元模型讨论了混凝土桥面板不同锈裂失效模型的控制因素(包括几何尺寸、钢筋位置等).

Val等［46］利用二维平面带孔洞的有限元模型研究了铁锈在自由膨胀阶段的填充量，并利用开裂时刻锈蚀量的试验值与有限元模拟得到的结果之差来反映铁锈填充的大小.

Saouma等［47-48］采用3种不同预设开裂路径的方法模拟了钢筋锈胀开裂的过程(见图9).基于均匀的环向节点位移，采用如下3组不同的加载方式进行试验:① 每个荷载步取为3.485 μm，该值等效于3个月的锈蚀.通过计算得到，1条裂缝模型的表面开裂需要12年，其表面裂宽为0.1248 mm.而对于包含3条裂缝的模型，其保护层表面开裂需要10年.② 每个荷载步取为2.720 μm.通过计算得到，1条裂缝模型的表面开裂同样需要12年.③ 每个荷载步取为1.360 μm.计算表明，仅需3.4年混凝土保护层表面就出现了裂缝.

图9 3种预设开裂路径［47-48］

Shaikh等［49］对3种钢筋混凝土梁进行了锈胀开裂的试验研究和数值模拟.结果表明，当普通钢筋混凝土梁的钢筋截面损失率达到1.5%时，混凝土保护层表面会出现锈胀裂缝;当钢筋截面损失率达到3%时，混凝土保护层将剥离.

Du等［50］在数值模拟的过程中考虑到了非均匀锈蚀的情况，采用如图10所示的3种不同加载方式来分别模拟均匀锈蚀和非均匀锈蚀，其中2种非均匀锈蚀径向位移分布是假设的.按照图10(b)和(c)所示的分布形式，环向最大位移与最小位移之比为5.模拟结果表明:内裂仅取决于钢筋直径和膨胀应力，而与钢筋的锈蚀类型和保护层厚度无关;混凝土保护层的外裂仅与保护层厚度有关，而且发生在保护层最薄的地方;贯通裂缝与保护层厚度与钢筋直径之比呈线性关系;非均匀锈蚀导致混凝土保护层开裂时的锈蚀量比非均匀锈蚀早，因此实际工程中的点蚀现象比均匀锈蚀对钢筋混凝土构件的威胁更大.

图10 3种不同锈蚀情形［50］

Jang等［51］利用数值模拟的方法着重研究了非均匀锈蚀导致的混凝土开裂情况，非均匀锈蚀的锈层分布形态是从锈峰处线性递减的.通过调整不同的荷载分布、模型的材料参数和几何尺寸，得出了混凝土保护层表面开裂时刻钢筋锈胀力与钢筋表面锈蚀范围对应的圆心角、钢筋直径、保护层厚度与钢筋直径之比以及混凝土抗拉强度之间的关系.

夏宁等［52］在假设锈蚀产物仅沿钢筋断面径向发生膨胀的前提下，提出钢筋圆孔边任意一点的锈胀位移可表示为

当0≤α≤π时

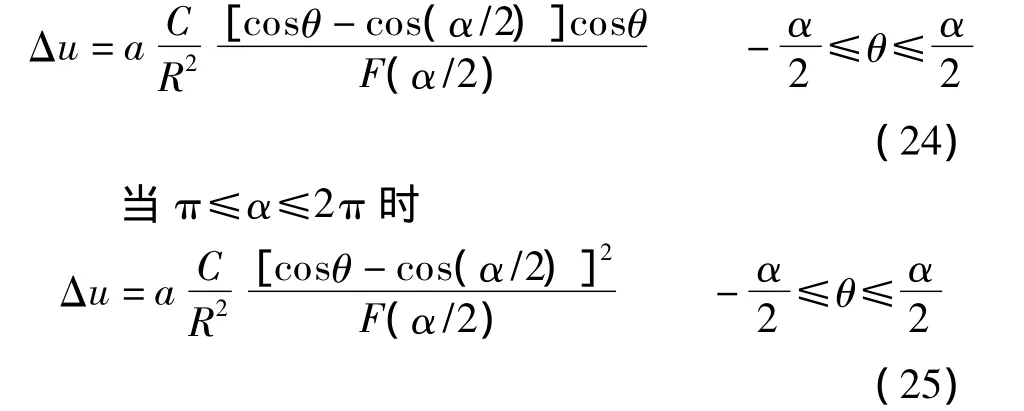
式中，F(α/2)=3sin(α/2)+sin3(α/2)－3(α/2)cos(α/2);θ为钢筋锈蚀轮廓线上任意一点的转角;a为锈蚀厚度系数，反映了钢筋表面的锈蚀程度.钢筋表面锈蚀轮廓线随α和a的变化情况见图11.

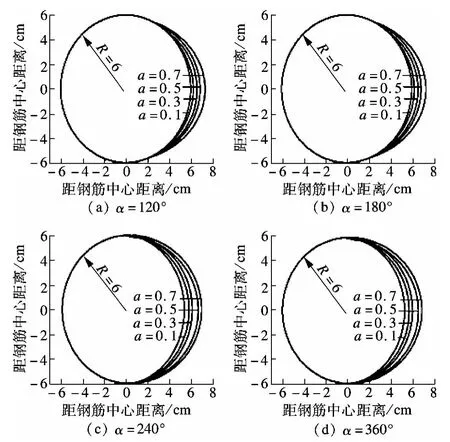
图11 钢筋表面锈蚀轮廓线［52］

笔者曾通过试验研究，分析得到沿着钢筋周边非均匀锈层厚度Tr的分布模型为［53］

式中，φ为钢筋周围的极坐标;a1，a2，a3分别为锈层的非均匀系数、扩展系数和均匀系数.

利用式(26)所示的锈层厚度解析模型作为有限元模型中位移荷载分布的依据，对锈蚀钢筋混凝土试件进行有限元分析，研究非均匀锈蚀胀裂过程［54］.根据有限元分析，可以得到钢筋非均匀锈蚀导致的周围混凝土的应力场分布状态、锈胀裂缝开展与分布状况、钢筋与混凝土界面锈胀力等试验方法无法测得的结果.有限元分析结果中的试件锈裂图和实际混凝土试件锈裂情况对比见图12.

图12 混凝土试件锈裂图和数值模拟结果对比［54］

3.2 数值模拟讨论

为了得到保护层因钢筋锈胀力产生的力学响应和裂缝开展状况，许多研究中利用了有限元分析方法，通过虚拟的内部压力或径向位移来模拟锈胀力，大部分非均匀锈蚀模型中都采用了假设的非均匀荷载/位移分布形式.应该看到，若采用的假设非均匀荷载分布与实际情况不一致，有限元模型得到混凝土锈裂模型的准确性也是令人质疑的;因此，钢筋与混凝土交界面上钢筋锈胀力的正确模拟，是实现混凝土锈裂过程数值模拟的关键所在.只有按照钢筋锈蚀产物真实的非均匀分布来模拟锈胀力荷载，才能得到锈蚀钢筋周围混凝土的应力场和裂缝开展状态等情况的合理描述.在后续的有限元模拟混凝土锈裂过程中，应考虑钢筋锈蚀非均匀分布的实际情况，将其作为位移荷载输入，以得到更符合实际情况的混凝土锈裂数值模型.

目前，有限元模拟基本采用混凝土内部带有圆孔的二维模型.利用该模型可以简化数值模拟，节省计算时间，同时可以在一定程度上较好地模拟锈胀裂缝由内而外的发展和裂缝开展过程.但是，二维模型无法考虑截面间的相互影响，也无法分析混凝土锈裂开展后的剥落情况.因此，混凝土锈裂的有限元模拟应从二维模型向三维模型发展.

4 研究展望

为推进钢筋锈蚀引起混凝土结构锈裂研究的发展，下述研究内容尚待深入:

1)铁锈填充区的定量研究.目前对于混凝土构件锈裂过程中铁锈填充行为的研究并不多见，尤其缺少定量的研究成果.如何建立铁锈填充区域和锈层积累之间的定量关系，还需要大量的试验研究工作.

2)钢筋非均匀锈蚀分布模型.在混凝土结构锈裂分析模型中，不但要考虑钢筋总锈蚀率，同时还应考虑锈蚀产物沿钢筋圆周的分布，即钢筋非均匀锈蚀分布情况.目前尚没有成熟的钢筋非均匀锈蚀分布模型，该模型的建立也需要大量的试验研究和分析.

3)荷载与环境耦合作用的考虑.现有的混凝土锈裂研究中，大多仅考虑钢筋锈蚀引起混凝土保护层锈裂，这与实际情况是不符合的.在后续的混凝土锈裂试验研究、理论分析和数值模拟中，应同时考虑环境与荷载的耦合作用.

4)箍筋对混凝土锈裂过程的影响.箍筋也会引起混凝土保护层锈裂，很多实际工程中箍筋锈胀裂缝往往比纵筋锈胀裂缝出现得更早.然而，目前的理论分析和数值模拟多采用二维模型来研究纵筋锈蚀引起的混凝土保护层开裂.箍筋锈蚀引起的混凝土保护层开裂以及箍筋对纵筋锈蚀引起混凝土开裂的影响，尚待深入进行.

5 结论

1)采用试验观测混凝土锈裂过程是直观、易行、有效的研究手段，但由于锈蚀混凝土构件材料的复杂性、混凝土锈裂试验方法的差异性等原因，仅根据有限试验数据拟合得到的经验公式对锈裂过程进行预测，还存在较大的局限性.

2)目前建立的混凝土锈胀开裂理论模型可以较好地描述理想圆柱体钢筋混凝土试件在均匀钢筋锈胀力作用下的锈裂行为.但是，对于实际工程中更常见的钢筋非均匀锈蚀、受荷载作用的混凝土结构锈裂情况，还尚未建立完善的预测模型.

3)要建立准确的混凝土锈裂模型，应对混凝土中的铁锈填充混凝土孔隙过程和钢筋/混凝土界面的锈层积累同时进行这一现象加以考虑;在混凝土锈胀裂缝发展到混凝土表面前，铁锈是不会填充到锈胀裂缝中的.基于这一发现，混凝土表面锈裂过程应采用二阶段理论来代替原来的三阶段理论.

4)有限元软件是研究混凝土锈胀开裂的一种有效手段，获取钢筋锈蚀非均匀分布的实际情况，以此作为位移荷载输入，是实现对混凝土锈裂过程正确模拟的关键所在.数值模拟应从原常用的混凝土内部带圆孔的二维模型向三维模型发展.

5)为更好地发展混凝土结构锈裂研究，还应深入进行钢筋混凝土界面铁锈填充区的定量研究，建立钢筋周围的锈层非均匀分布模型，并在锈裂研究中考虑外部荷载及构件内箍筋的影响.

References)

［1］Andrade C，Alonso C，Molina F J.Cover cracking as a function of bar corrosion:part 1—experimental test［J］.Materials and Structures，1993，26(8):453-464.

［2］Alonso C，Andrade C，Rodriguez J，et al.Factors controlling cracking of concrete affected by reinforcement corrosion［J］.Materials and Structures，1998，31(7):435-441.

［3］Rodriguez J，Ortega L M，Casal J，et al.Corrosion of reinforcement and service life of concrete structures［C］//Proceedings of the 7th International Conference on Durability of Building Materials and Components.London，1996:117-126.

［4］Webster M P，Clark L A.The structural effect of corrosion—an overview of the mechanism［C］//Proceedings of 2000 Concrete Communication.Birmingham，UK，2000:409-421.

［5］张伟平.混凝土结构的钢筋锈蚀率损伤预测及其耐久性评估［D］.上海:同济大学土木工程学院，1999.

［6］Oh B H，Kim K H，Jang B S.Critical corrosion amount to cause cracking of reinforced concrete structures［J］.ACI Materials Journal，2009，106(4):333-339.

［7］Liu Y P，Weyers R E.Modeling the time-to-corrosion cracking in chloride contaminated reinforced concrete structures［J］.ACI Material Journal，1998，95(6):675-681.

［8］Rasheeduzzaf A R，Al-Saadoun S S，A1-Gahtani A S.Corrosion cracking in relation to bar diameter，cover，and concrete quality［J］.Journal Material and Civil Engineering，1992，4(4):327-343.

［9］Vu K，Stewart M G，Mullard J.Corrosion-induced cracking:experimental data and predictive models［J］.ACI Structural Journal，2005，102(5):719-726.

［10］Vidal T，Castel A，Francois R.Analyzing crack width to predict corrosion in reinforced concrete［J］.Cement and Concrete Research，2004，34(1):165-174.

［11］Zhang R，Castel A，Francois R.Concrete cover cracking with reinforcement corrosion of RC beam during chloride-induced corrosion process［J］.Cement and Concrete Research，2010，40(3):415-425.

［12］王深.钢筋混凝土结构锈胀裂缝的研究及耐久性评估［D］.上海:同济大学土木工程学院，2000.

［13］Mullard J A，Stewart M G.Corrosion-induced cover cracking of RC structures:new experimental data and predictive models［R］.Callaghan，Australia:The University of Newcastle，2009.

［14］夏晋.锈蚀钢筋混凝土结构力学性能研究［D］.杭州:浙江大学建筑工程学院，2010.

［15］赵羽习，金伟良.钢筋锈蚀导致混凝土构件保护层胀裂的全过程分析［J］.水利学报，2005，36(8):939-945.Zhao Yuxi，Jin Weiliang.Analysis on corrosion-induced concrete cover cracking process［J］.Journal of Hydraulic Engineering，2005，36(8):939-945.(in Chinese)

［16］陆春华，赵羽习，金伟良.锈蚀钢筋混凝土保护层锈胀开裂时间的预测模型［J］.建筑结构学报，2010，31(2):85-92.Lu Chunhua，Zhao Yuxi，Jin Weiliang.Modeling of time to corrosion-induced cover cracking in reinforced concrete structures［J］.Journal of Building Structures，2010，31(2):85-92.(in Chinese)

［17］余江.混凝土结构锈裂损伤分析与试验研究［D］.杭州:浙江大学建筑工程学院，2011.

［18］Michel A，Brad J P，Mette R，et al.Monitoring reinforcement corrosion and corrosion-induced cracking using non-destructive X-ray attenuation measurements［J］.Cement and Concrete Research，2011，41(11):1085-1094.

［19］Caré S，Nguyen Q T，L'Hostis V，et al.Mechanical properties of the rust layer induced by impressed current method in reinforced mortar［J］.Cement and Concrete Research，2008，38(8/9):1079-1091.

［20］Wong H S，Zhao Y X，Karimi A R，et al.On the penetration of corrosion products from reinforcing steel into concrete due to chloride-induced corrosion［J］.Corrosion Science，2010，52(7):2469-2480.

［21］Zhao Y X，Yu J，Wu Y Y，et al.Critical thickness of rust layer at inner and out surface cracking of concrete cover in reinforced concrete structures［J］.Corrosion Science，2012，59:316-323.

［22］Zhao Y X，Wu Y Y，Jin W L.Distribution of millscale on corroded steel bars and penetration of steel corrosion products in concrete［J］.Corrosion Science，2012，66:160-168.

［23］Bazan Z P.Physical model for steel corrosion in sea structures applications［J］.Journal of Structural Division，1979，105(6):1155-1166.

［24］郑建军，周欣竹.钢筋混凝土结构锈蚀损伤的解析解［J］.水利学报，2004，35(12):62-68.Zhen Jianjun，Zhou Xinzhu.The analytical solution of the corrosion damage of reinforced concrete structures［J］.Journal of Hydraulic Engineering，2004，35(12):62-68.(in Chinese)

［25］Zhao Y X，Jin W L.Modeling the amount of steel corrosion at the cracking of concrete cover［J］.Advances in Structural Engineering，2006，9(5):687-696.

［26］Zhao Y X，Yu J，Jin W L.Damage analysis and cracking model of reinforced concrete structures with rebar corrosion ［J］.Corrosion Science，2011，53(10):3388-3397.

［27］吴瑛瑶.混凝土结构二阶段理论及裂缝开展研究［D］.杭州:浙江大学建筑工程学院，2013.

［28］Bhargava K，Ghosh A K，Mori Y，et al.Modeling of time to corrosion-induced cover cracking in reinforced concrete structures［J］.Cement and Concrete Research，2005，35(11):2203-2218.

［29］Bhargava K，Ghosh A K，Mori Y，et al.Analytical model for time to cover cracking in RC structures due to rebar corrosion［J］.Nuclear Engineering and Design，2006，236(11):1123-1139.

［30］Pantazopoulou S J，Papoulia K D.Modeling covercracking due to reinforcement corrosion in RC structures［J］.Journal of Engineering Mechanics，2001，127(4):342-351.

［31］Chernin L，Val D V，Volokh K Y.Analytical modeling of concrete cover cracking caused by corrosion of reinforcement［J］.Materials and Structures，2010，43(4):543-556.

［32］Maaddawy T E，Soudki K.A model for prediction of time from corrosion initiation to corrosion cracking［J］.Cement and Concrete Composites，2007，29(3):168-175.

［33］Kim K H，Jang S Y，Jang B S，et al.Modeling mechanical behavior of reinforced concrete due to corrosion of steel bar［J］.ACI Structural Journal，2010，107(2):106-113.

［34］王海龙，金伟良，孙晓燕.基于断裂力学的钢筋混凝土保护层锈胀开裂模型［J］.水利学报，2008，39(7):863-869.Wang Hailong，Jin Weiliang，Sun Xiaoyan.Corrosion-induced cracking model of reinforced concrete cover based on fracture mechanics［J］.Journal of Hydraulic Engineering，2008，39(7):863-869.(in Chinese)

［35］Li C Q，Melchers R E，Zheng J J.Analytical model for corrosion-induced crack width in reinforced concrete structures［J］.ACI Structural Journal，2006，103(4):479-487.

［36］王显利，郑建军，吴智敏.钢筋临界锈胀力预测的断裂模型［J］.水力发电，2007，33(2):49-52.Wang Xianli，Zheng Jianjun，Wu Zhimin.Fracture predicting model for the critical expansion force of reinforced［J］.Water Power，2007，33(2):49-52.(in Chinese)

［37］罗晓辉，卫军，徐港.钢筋锈胀时混凝土保护层损伤模型［J］.华中科技大学学报:自然科学版，2008，36(6):115-118.Luo Xiaohui，Wei Jun，Xu Gang.Damage model of concrete cover with steel corrosion［J］.Journal of Huazhong University of Science and Technology:Natural Science Edition，2008，36(6):115-118.(in Chinese)

［38］Li S C，Wang M B，Li S C.Model for cover cracking due to corrosion expansion and uniform stresses at infinity［J］.Applied Mathematical Modeling，2008，32(7):1436-1444.

［39］Malumbela G，Alexander M，Moyo P.Model for cover cracking of RC beams due to partial surface steel corrosion［J］.Construction and Building Materials，2011，25(2):987-991.

［40］冯瑞，袁迎曙，朱辉，等.钢筋非均匀锈胀力的理论分析［J］.徐州工程学院学报，2008，23(4):5-10.Feng Rui，Yuan Yingshu，Zhu Hui，et al.Theoretical analysis of expansion induced by steel non-uniform corrosion ［J］.Journal of Xuzhou Institute of Technology，2008，23(4):5-10.(in Chinese)

［41］Zhao Y X，Ren H Y，Dai H，et al.Composition andexpansion coefficient of rust based on X-ray diffraction and thermal analysis［J］.Corrosion Science，2011，53(5):1646-1658.

［42］Zhao Y X，Dai H，Ren H Y，et al.Experimental study of the modulus of steel corrosion in a concrete port［J］.Corrosion Science，2012，56(1):17-25.

［43］Dagher H J，Kulendran S.Finite element modeling of corrosion damage in concrete structures［J］.ACI Structural Journal，1992，89(6):699-708.

［44］Molina F J，Alonso C，Andrade C.Cover cracking as a function of rebar corrosion:part 2—numerical model［J］.Mater Struct，1993，26(9):532-548.

［45］Zhou K，Martin-Perez B，Lounis Z.Finite element analysis of corrosion-induced cracking，spalling and delamination of RC bridge decks［C］//Proceedings of the 1st Canadian Conference on Effective Design of Structures.Hamilton，Ontario，Canada，2005:187-196.

［46］Val D V，Chernin L，Stewart M G.Experimental and numericalinvestigation ofcorrosion-induced cover cracking in reinforced concrete structures［J］.Journal of Structural Engineering，ASCE，2009，135(4):376-385.

［47］Saouma V E，Chang S Y.Numerical simulation of reinforced concrete deterioration due to steel corrosion，freezing-thawing and mechanical load effects［C］//Proceedings of the 3rd IABMAS Workshop on Life-Cycle Cost Analysis and Design of Civil Infrastructures Systems.Lausanne，Switzerland，2003:102-107.

［48］Hansen E J，Saouma V E.Numerical simulation of reinforced concrete deterioration:partⅡ—steel corrosion and concrete cracking ［J］.ACI Material Journal，1999，96(3):331-338.

［49］Shaikh F，Uddin A，Mohamed M，et al.Cover cracking of reinforced concrete beams due to corrosion of steel［J］.ACI Materials Journal，2007，104(2):153-161.

［50］Du Y G，Chan A H C，Clark L A.Finite element analysis of the effects of radial expansion of eroded reinforcement［J］.Computers and Structures，2006，84(13/14):917-929.

［51］Jang B S，Oh B H.Effects of non-uniform corrosion on the cracking and service life of reinforced concrete structures［J］.Cement and Concrete Research，2010，40(9):1441-1450.

［52］夏宁，任青文.混凝土中钢筋不均匀锈胀的数值模拟及锈蚀产物量的预测［J］.水利学报，2006，37(1):70-74.Xia Ning，Ren Qingwen.Numerical simulation of nonuniform corrosion of steel bar in concrete and the prediction of corrosion products［J］.Journal of Hydraulic Engineering，2006，37(1):70-74.(in Chinese)

［53］Zhao Y X，Hu B Y，Jin W L.Non-uniform distribution of rust layer around steel bar in concrete［J］.Corrosion Science，2011，53(12):4300-4308.

［54］Zhao Y X，Karimi A R，Wong H S，et al.Comparison of uniform and non-uniform corrosion induced damage in reinforced concrete based on a Gaussian description of the corrosion layer［J］.Corrosion Science，2011，53(9):2803-2814.