WPDM-CDMA 系统中的LS 与MMSE信道估计算法仿真分析

李姣军 ，陈安志 ，苏理云 ，唐 娜，张 婷

(重庆理工大学 a.电子信息与自动化学院;b.数学与统计学院，重庆 400054)

小波包变换多载波码分多址(WPDM-CDMA)将小波包多载波调制技术与CDMA 技术有效地结合在一起，以充分利用二者的优势获取更好的系统性能［1-3］。WPDM-CDMA 能利用频率分集效果，同时具备较强的抗多径干扰能力［4］，己成为未来宽带多媒体无线通信系统中最合适的备选方案之一。在WPDM-CDMA 系统中，由于无线信道在时域和频域具有选择性衰落的特性，因此必须通过信道估计来获得信道信息。文献［5］提出一种基于小波包变换的多载波CDMA，并介绍了其基本结构。文献［6-7］利用信道估计得到小波包多载波系统信道的冲激响应，并通过小波包变换得到信道的统计特性，但是对于系统的信道估计算法没有做具体的叙述和说明。文献［8］提出了一种适于小波包多载波系统信道估计的导频插入方法。文献［9］提到MMSE 估计算法具有最好的性能，但也具有最高的算法复杂度。文献［10］提到LS 信道估计是在最小均方误差准则下所有无偏估计方法中最有效的，而LS 估计算法由于忽略了噪声项的影响，使得其在信噪比较低时估计性能较差。本文以WPDM-CDMA 系统为模型，通过理论公式推导，分析了2种经典的LS 与MMSE 信道估计方法，并在Matlab 下进行仿真分析，探讨在WPDM-CDMA 系统中的信道估计问题，并给出数值分析结果。

1 WPDM-CDMA 系统

基于导频信道估计的WPDM-CDMA 系统的模型［3-5］如图1所示。输入二进制信息比特(用户信息)，根据需要选择不同的调制方式(如QPSK或16QAM)进行星座映射，得到信号空间的复数坐标(信息序列)，接着经过串/并变换变为N 路并行比特流。N 是由信道的频谱特性确定的子信道个数。导频信号根据不同的导频模式分别插入到N 路信号中，再经过小波包逆变换后送入信道进行发送。

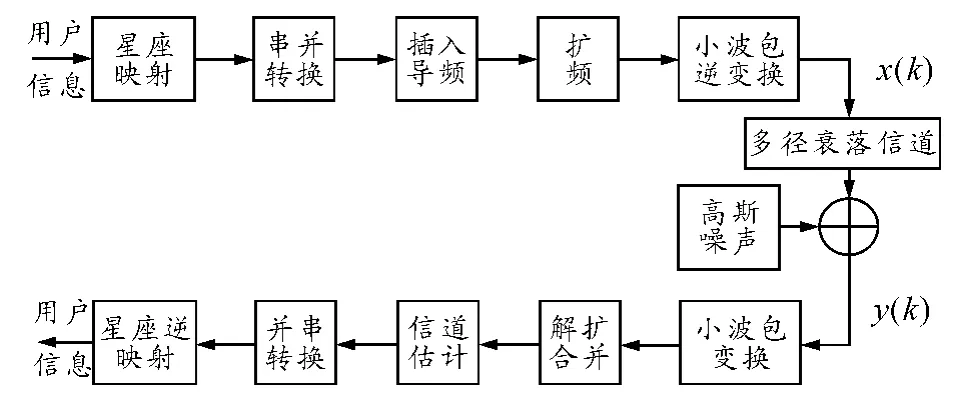
图1 WPDM-CDMA 系统模型

经过小波包逆变换传入信道的信号x(k)可以表示为［8］:

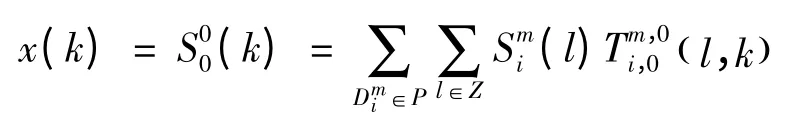
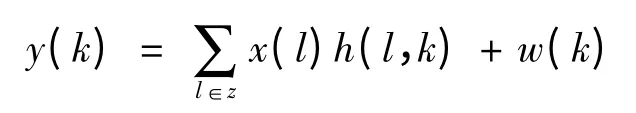
式中:w(k)是高斯噪声;h 是信道的冲激响应。

相应地，在接收端解调的信号经过小波包逆变换，通过解扩合并、信道估计、并/串转换、星座逆映射后，最终在满足一定的误码要求下恢复原始信号。

2 信道估计算法

在WPDM-CDMA 系统中，由于信息传输速率较高，并且在接收端需使用相干解调技术获得较高性能，一般采用非盲估计。其基本过程:在发送端适当位置插入导频，接收端利用导频恢复出导频位置的信道信息。在信道估计的各种算法中，典型的有LS 和MMSE 算法。LS 算法的准则是求得接收与发送端的最小平方误差;而MMSE 算法的准则是求得两者间的最小均方误差。

信道的估计过程如图2所示。e(n)为估计误差，信道估计算法就是要使均方误差E［|e(n)|2］最小，同时还要降低算法的复杂度。

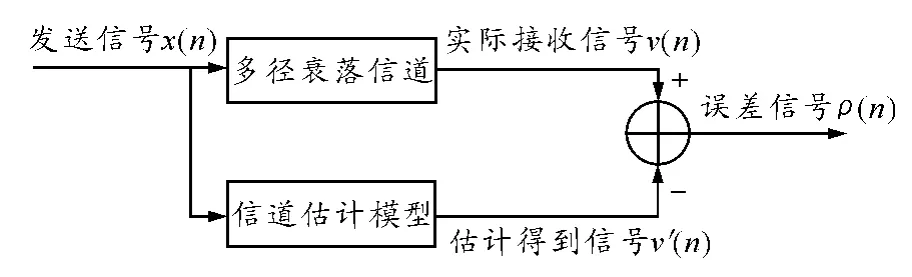
图2 信道估计模型

设系统的输入导频信号为X(k)，k=0，1，…，M-1，经过小波包综合后(小波逆变换)输出信号为x(n)，n=0，1，…，M-1，信道传输函数为h(n)，n=0，1，…，M-1，其频率响应为H(k)，k=0，1，…，M-1;高斯噪声为w(n)，n=0，1，…，M-1，其频率响应为W(k)，k=0，1，…，M-1;接收的导频信号为y(n)，n=0，1，…，M-1，经过小波包分解后输出［7］为Y(k)，k=0，1，…，M-1，则有Y(k)=X(k)H(k)+W(k)。

2.1 LS 信道估计算法

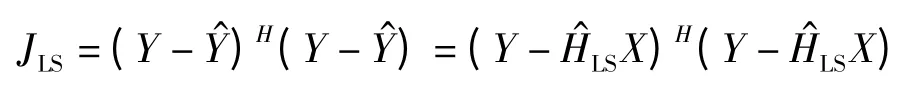
2.2 MMSE 信道估计算法

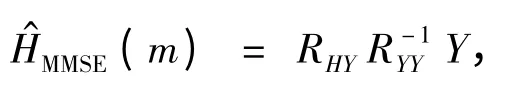
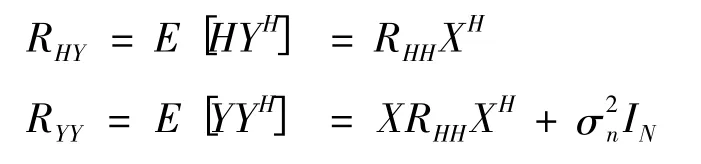
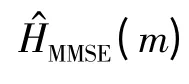
3 性能仿真

本文在Matlab7.4 软件下，对LS 算法和MMSE算法进行仿真，衡量信道估计效果的准则是均方误差(MSE，mean square error)和误码率(SER，symbol error rate)。仿真中采用的WPDM-CDMA 系统参数如下:采用BPSK 调制，Walsh 码作为地址码，采用多径衰落AWGN 信道，系统共传送1 000个WPDM符号，每个符号中子载波数为32。

从图3 和图4 仿真结果可得知:在信噪比值较小时LS 估计有较大均方误差和误码率，说明该算法对噪声比较敏感;随着信噪比的提高，LS 算法估计性能有了较大的改善。在相同的SNR 时刻点，MMSE 算法的均方差和误码率较LS 估计算法要低，特别在低信噪比时，MMSE 算法性能远优于LS 算法。然而遗憾的是:MMSE 算法需要求解Q 矩阵的逆，计算量过大，复杂度过高，从算法编写和实现的角度而言，不适合实际中的应用，所以实际中应用最多的还是LS 信道估计算法。

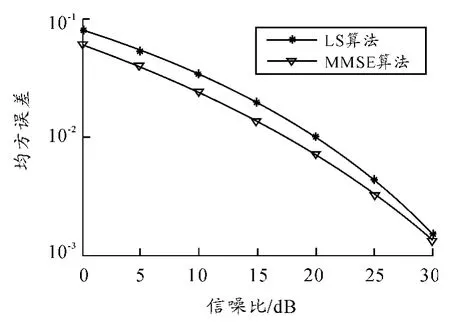
图3 两种信道估计方法的均方误差比较

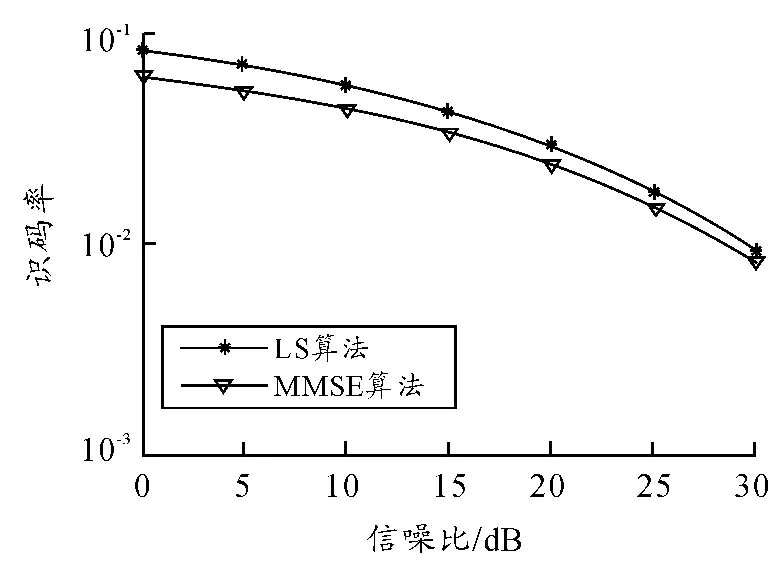
图4 两种信道估计方法的误码率比较

4 结束语

本文通过Matlab 建立WPDM-CDMA 模型，在这个系统之上分析了2种经典信道估计算法LS和MMSE，对这两种估计算法各自的优、缺点作了进一步的分析与比较，并在多径衰落AWGN 信道下，对LS 和MMSE 信道估计算法进行了仿真和比较。数值分析结果表明:在性能上MMSE 算法远优于LS 算法，但MMSE 算法复杂度远远高于LS算法，因此在实际应用时需要根据具体情况采用相应的信道估计方法。

［1］吴伟陵.移动通信中的关键技术［M］.北京：北京邮电大学，2000.

［2］WANG Rong，WEI Jibo，CHENG Shixin.A MC-CDMA system based on optimal wavelet packets decomposition and its performance［C］//ICCT.1998.

［3］李姣军，唐娜.WPDM-CDMA 系统中的子载波分配算法研究［J］.西南大学学报，2012，34(7)：125-129.

［4］李姣军，李恒，苏理云.一种快速自适应最优小波包基搜索算法［J］.现代电子技术，2011，34(11)：72-75.

［5］杨慰民，毕光国.基于小波包变换的多址通信［J］.通信学报，1999.20(3)：28-35.

［6］窦怀宇，毕光国.最佳小波包多载波调制解调技术［J］.通信学报，2000，21(6)：24-30.

［7］孙懿，郝久玉.基于小波包变换多载波调制通信系统的均衡算法［J］.计算机应用，2010，30(4)：865-867.

［8］杨闽，法卢克，李奕.一种适于小波包多载波系统导频信道估计的方法［J］.天津大学学报，2009，42(5)：438-443.

［9］霍丽萍.基于小波包变换的多载波调制系统的符号同步和信道估计［M］.天津：天津大学，2005.

［10］张乃元.LTE 系统中的信道估计技术研究［M］.北京：北京邮电大学，2010.