图像处理中的正交变换探讨
2013-08-14刘舜鑫刘少卿
刘舜鑫,刘少卿
(工业和信息化部电子第五研究所,广东 广州 510610)
0 引言
图像处理是指用计算机对图像进行分析,以达到所需结果的技术,又被称为影像处理。平常所说的图像处理一般指数字图像处理。数字图像是指用数字摄像机、扫描仪等设备经过采样和数字化得到的一个大的二维数组,该数组的元素被称为像素,其值为一整数,被称为灰度值。图像处理技术的主要内容包括图像压缩,增强和复原,匹配、描述和识别3个部分[1]。
图像变换是图像处理技术的重要工具。为了有效和快速地对图像进行处理和分析,图像变换将原定义在图像空间的图像以某种形式转换到另外一些空间,并利用这些空间的特有性质更方便地进行加工,最后再变换回图像空间以得到所需的效果。正交变换改变图像的表示域及表示数据,给图像处理工作带来了极大的方便。利用这个工具,可以对图像的频谱进行各种各样的处理。
1 正交变换的两种定义
a)定义1:欧氏空间V上的一个线性变换σ被称为正交变换,如果它保持向量的长度不变,即对任意ξ∈V,均有
b)定义2:欧氏空间V上的一个线性变换σ被称为正交变换,如果它保持向量的内积不变,即对任意 ξ,η∈V,均有(σ(ξ),σ(η))=(ξ,η)。
正交变换最邻近的一种概念是线性变换,而保持向量的长度不变与保持向量的内积不变分别是正交变换的两个特征。在σ是线性变换的前提下,可以证明这两个特征是等价的,所以定义1与定义2所描述的概念的内涵是一致的。
常见的正交变换有离散傅里叶变换(DFT)、离散沃什一哈达玛变换(DWHT)、离散余弦变换(DCT)和斜变换(ST)、 霍特林变换(K-L)等[2]。
1.1 傅立叶变换
傅立叶变换是数字图像处理技术的基础,其通过时空域和频率域来回切换图像,对图像的信息特征进行分析和提取,简化了计算工作量,被喻为描述图像信息的第二种语言,广泛地应用于图像变换、图像编码与压缩、图像分割和图像重建中。因此,深入研究和掌握傅立叶变换及其扩展形式的特性是很有价值的。
1.1.1 傅立叶变换的两种定义
设R表示实数全体,L2(R)表示在R上的勒贝格平方可积的函数全体。L2(R)中的函数在通信学科中又被称作为能量有限信号。对f(x)∈L2被称作为f的能量。
本文主要讨论L2(R)中函数的傅立叶变换的定义。这两种定义都与积分有关。虽然f(x)∈L1(R),积分(x)exp(-iωx)dx一定收敛,但 F(ω)不一定属于L1(R)。因此,F(ω)的傅立叶逆变换不一定存在。如果f(x)∈L2(R),则积分(-iωx)dx不一定存在。 但是,若 f(x)∈L2(R),则对任意自然数N,f(x)在区间[-N,N]上绝对可积,于是dx有意义,而且函数序列 {FN(ω)}N是 L2(R)中的柯西序列。由于L2(R)是完备的,因此函数序列 {FN(ω)}N收敛于L2(R)中惟一的极限函数。
a)定义1 设f(x)∈L2(R),则f的傅立叶变换定义为:
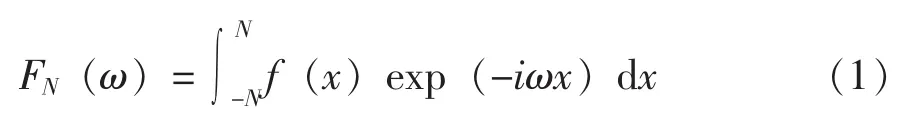
在L2(R)中的柯西极限,记为:
为方便起见,通常将上述极限简记为:
其对应的傅立叶逆变换定义为:
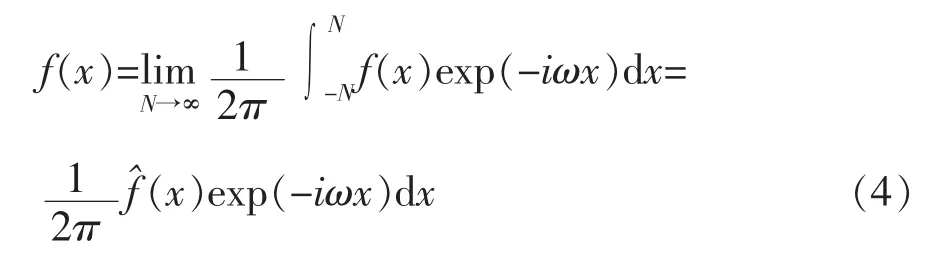
b)定义2 设f(x)∈L2(R),则f的傅立叶变换定义为:
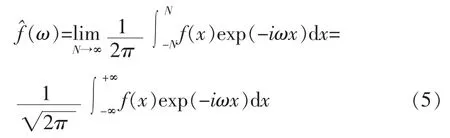
其对应的傅立叶逆变换定义为:

(注:按照定义1,傅立叶变换是从L2(R)到L2(R)上的有界可逆线性算子。按照定义2,傅立叶变换是从L2(R)到L2(R)上的酉算子。如果记第一种傅立叶变换为F1[f](ω),第2种傅立叶变换为 F2[f](ω),则 F1[f](ω)=2πF2[f](ω)。)
1.1.2 快速傅立叶变换及其效率评价
快速傅立叶变换( FFT:Fast Fourier Transform)是离散傅立叶变换(DFT:Discrete Fourier transform)的快速算法,它是根据离散傅立叶变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进而获得的。它对傅立叶变换的理论并没有新的发现,但是,对于在计算机系统或者说数字系统中应用离散傅立叶变换,可以说是提高了一大步。
设Xn为N项的复数序列,由DFT变换,任一Xi的计算都需要N次复数乘法和N-1次复数加法,而一次复数乘法等于四次实数乘法和两次实数加法,一次复数加法等于两次实数加法,即使把一次复数乘法和一次复数加法定义成一次“运算”(四次实数乘法和四次实数加法),那么求出项N复数序列的Xi,即N点DFT变换大约就需要N2次运算。当N=1024点甚至更多的时候,需要N2=1048576次运算。在 F FT中,利用ωn的周期性和对称性,把一个N项序列(设N为偶数),分为两个N/2项的子序列,每个N/2点DFT变换需要(N/2)2次运算,再用N次运算把两个N/2点的DFT变换组合成一个N点的DFT变换。这样变换以后,总的运算次数就变成N+2*(N/2)2=N+N2/2。继续上面的例子,N=1024时,总的运算次数就变成了525312次,节省了大约50%的运算量。而如果我们将这种“一分为二”的思想不断地进行下去,直到分成两两一组的DFT运算单元,那么N点的DFT变换就只需要N*log2N次的运算,N=1024点时,运算量仅有10240次,是先前的直接算法的1%,点数越多,运算量的节约就越大,这就是 F FT的优越性[3]。
2 离散余弦变换
2.1 问题的起源
离散余弦变换是N.Ahmed等人在1974年提出的正交变换方法。它常被认为是对语音和图像信号进行变换的最佳方法。由于近年来数字信号处理芯片的发展,加上专用集成电路设计上的优势,这就牢固地确立离散余弦变换在目前图像编码中的重要地位,成为H.261、JPEG、MPEG等国际上公用的编码标准的重要环节。在视频压缩中,最常用的变换方法是DCT,DCT被认为是性能接近K-L变换的最佳变换,该变换编码的主要特点有:
1)在变换域里的视频图像要比空间域里简单;
2)视频图像的相关性明显地下降,信号的能量主要集中在少数几个变换系数上,采用量化和熵编码可有效地压缩其数据;
3)具有较强的抗干扰能力,传输过程中的误码对图像质量的影响远小于预测编码。
2.2 离散余弦变换的基本概念
DCT利用傅立叶变换的性质,采用图像边界褶翻将图像变换为偶函数形式,然后对图像进行二维傅立叶变换,变换后仅包含余弦项,所以称之为离散余弦变换。
2.3 离散余弦变换算法
DCT算法需要的计算量依赖于矩阵的大小,随着N的增大,需要的计算处理时间将迅速地延长。实际上不可能在整个图像上执行DCT,如果N=256,对256×256样值进行DCT变换所需要的计算量之大,达到了使计算无法实时实现的程度。实际上,DCT的实现是将图像分割成许多8×8的小块,对各个小块进行DCT计算。虽然块尺寸增大会得到更好的压缩,但研究表明,像素之间的相关性很快趋于减弱,离预测点15个或20个像素位以外的像素对预测器来说用处不大。这意味着64×64的DCT块比起将它分成16×16这4个子块不会有更好的压缩。在JPEG和MPEG方案中选用8×8的子块,64个数据称为一个数据单元,按顺序进入编码器。
另外,DCT有快速算法,二维快速余弦变换(2D-FCT)是把8×8块不断地分成更小的无交叠子块,直接对数据块作运算操作。
在进行DCT之前,二维空间图像亮度数据通常较高,为了降低传输位率,应先进行向下的电平移位。设原样值的采样精度为P位,是无符号整数,输入之前把[0,2P-1]范围的无符号整数变成[-2P-1,2P-1-1]范围的有符号整数,以此作为DCT的输入。在解码时,再把经DCT反变换得到的一系列8×8样值子块的数值范围,由[-2P-1,2P-1-1]变回到[0,2P-1]范围,获得重建图像[4]。
3 两种变换结果的比对
3.1 傅立叶变换的实验结果
a)实验1
用随机生成的一个8×8矩阵作为时域离散信号输入,结果如图1所示(左图为时域信号,右图为频域信号)。
随机产生的DFT输入信号(8×8矩阵):


图1 傅立叶变换的时、频域信号对比图
DFT输出信号(Fx):
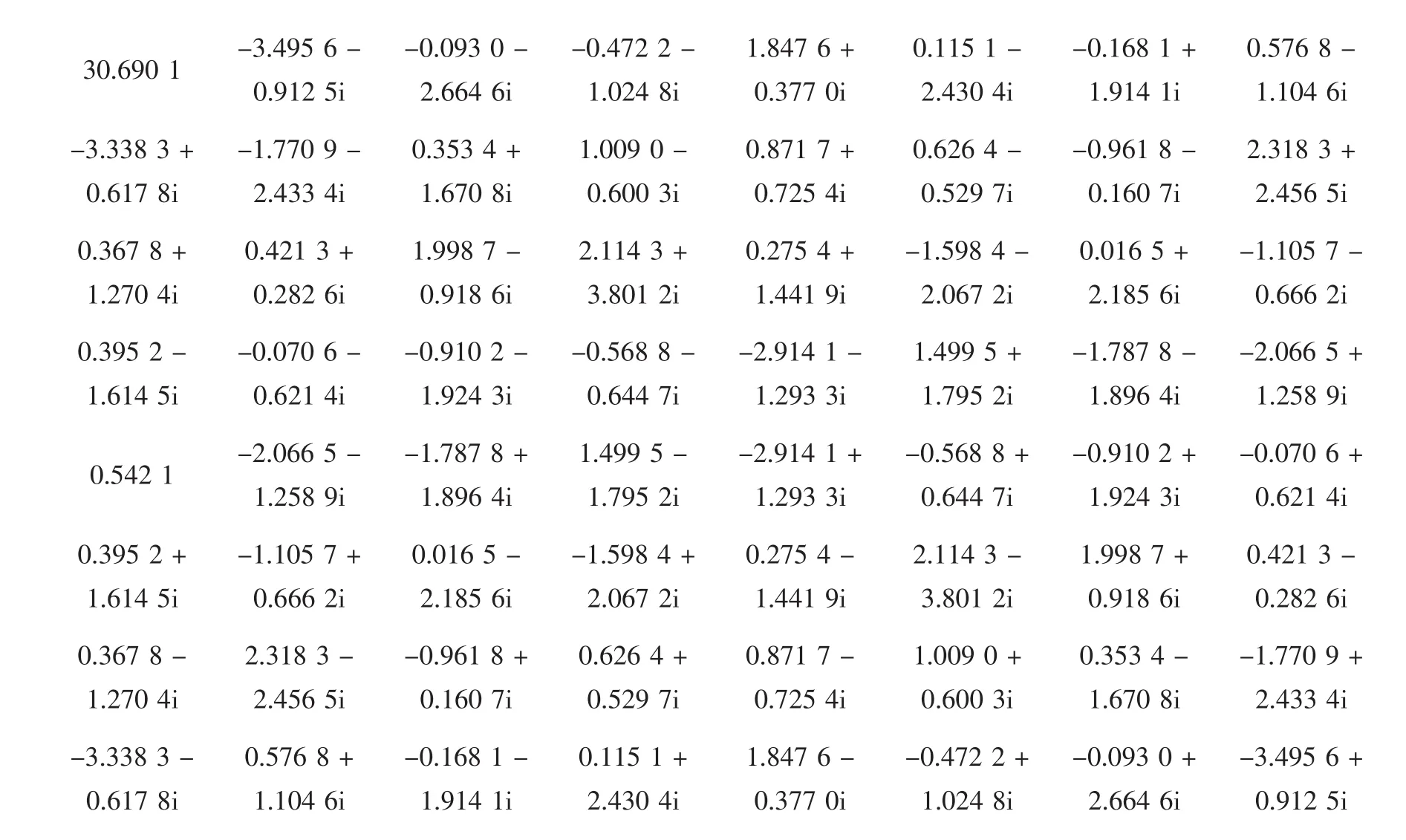
如图1所示,经傅立叶变换以后,频域信号主要集中在0~5之间即傅立叶变换后图像大部分能量集中在中间。
b)实验2
用C++程序对图像(如图2所示)进行傅立叶变换,从频谱图中更直观地进行观察、分析。
图3所示的亮点表示低频信号,利用傅立叶变换这个工具,可以对图像的频谱进行各种各样的处理,如滤波、降噪和增强等。

图2 原始图像

图3 DFT变换后的频谱
如图4所示,经离散余弦变换以后,频信号主要集中在0~0.5之间即离散余弦变换后图像大部分能量集中在左上角。
3.2 离散余弦变换的实验结果
随机产生的DCT输入信号(8×8矩阵):
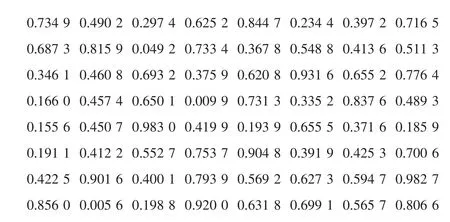
DCT输出信号(Fx):
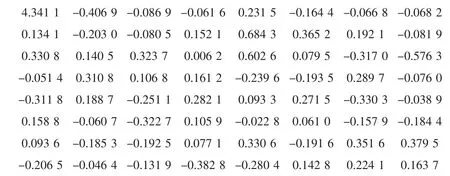
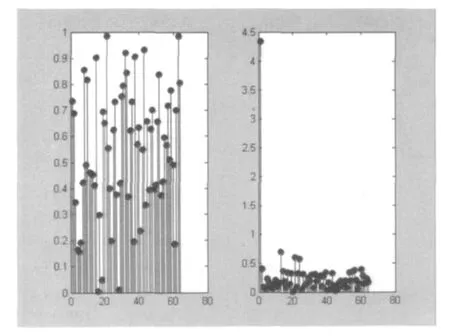
图4 离散余弦变换的时、频域信号对比图
图5所示的亮点表示低频信号,从图中可以看到图像的低频能量都集中在左上角区域,而向着右下角方向,频率越来越高。与图3的离散傅立叶变换频谱图进行比较可以发现,高低频的能量集中在不同的区域,这主要是因为离散傅立叶变换的变换核是复数,而离散余弦变换的变换核实际上是取其实部的原因。

3.3 两种变换结果的比较
为了更加直观、清楚地对比两种变换后频域的变化情况,现以一个随机矩阵作为输入信号,并同时对其进行DFT与DCT变换,实验结果如图6所示。
随机产生的输入信号(4×4矩阵):
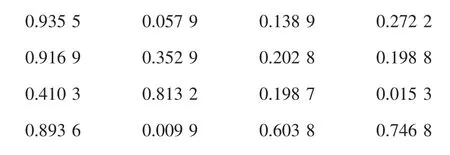
DFT输出信号(Fx1):

DCT输出信号(Fx2):

如图6所示,可以很明显地看出离散余弦变换的信号相对集中,即是对图像做离散余弦变换以后,大部分的能量集中在左上角[5]。
4 结束语

离散余弦变换实际上是傅立叶变换的实数部分,但是它比傅立叶变换有更强的信息集中能力。对于大多数自然的图像,离散余弦变换能将大多数的信息放到较小的系数上去,因此就更能提高编码的效率。同时,由于利用DCT的能量压缩特性,仅使用一部分DCT系数就可以重建信号,所以与傅立叶变换相比较,其失真比较小。
[1]燕卫.正交变换在图像处理技术上的应用[J].福州电视大学学报,2002,8(2):12-16.
[2]候维民,刘松涛.关于正交变换两种定义方式的探讨[J].高等数学研究学报,2005,8(1):44-45.
[3]王晓东,王荣芝.傅立叶变换在图像处理中的应用[J].牡丹江师范学报,2004,5(6):16-19.
[4]鲁业频,李凤亭,朱仁义,等.基于DCT编码的新进展[J].中国图象图形学报,2004,9(1):1-9.
[5]刘维.精通Matlab与C/C++混合程序设计[M].北京:北京航空航天大学出版社,2008.
