可靠性测验先验分布超参数确定方法

甄昕，丁力军

（1.中国人民解放军92941部队93分队，辽宁 葫芦岛 125001；2.中国人民解放军92493部队98分队，辽宁 葫芦岛 125001）

0 引言

一直以来，由于海军战术导弹的造价高昂，其设计定型试验或者鉴定试验都是在小样本条件下进行的。在对导弹战技术指标特别是一些可靠性指标作评定时，只依靠从定型试验或鉴定试验获得的子样信息通常是不够的。为了解决设计定型试验或鉴定试验子样不足的问题，目前常用的方法是：对于前期有研制试验的（如设计定型试验），从研制试验中获得先验信息，结合定型试验现场信息，采用Bayes小样本理论对可靠性指标作出评定；对于没有研制试验的（如大部分鉴定试验），可采用专家打分法来获取先验信息，结合鉴定试验的现场信息，采用Bayes小样本理论对可靠性指标作出评定。

Bayes小样本理论的一个核心问题是如何从先验信息中得到参数的先验分布，然后结合现场信息利用Bayes公式得到后验分布，最终依据参数的后验分布进行统计推断或决策。导弹飞行试验可靠性参数概率分布一般分为两类：1）（如飞行可靠度、单发命中概率等）服从二项分布，此类参数的先验分布一般为β（a，b）分布；2）（如失效率λ等）服从指数分布，此类参数的先验分布一般为Γ（c，d）分布。

在利用Bayes小样本理论对导弹飞行试验可靠性指标进行评定时，需要通过其先验信息来确定先验分布中的参数值，也就是需要确定所谓的 “先验超参数”。工程上确定先验分布超参数，可用分位数确定先验超参数的方法和专家知识确定超参数的方法[1]。

1 分位数法

分位数法是根据不同的置信概率对于不同的参数是先验分布分位数来确定先验分布超参数值。

假设评定导弹上某一电子产品的失效率λ，进行有替换定时截尾试验，总工作时间为τ，在工作期间共出现z次失效。

失效率λ的共轭先验分布为Γ（c，d）[2]，即：

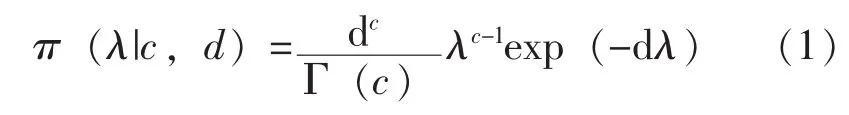
其中，λ＞0，c＞0，d＞0，c和 d 为先验超参数，其确定方法如下：

a）给定不同的置信概率γ1和γ2，根据先验信息确定产品的随机化最优置信上限λu1和λu2随机化最优置信上限λu，可依据不完全Γ函数的形式求解[3]，即有：

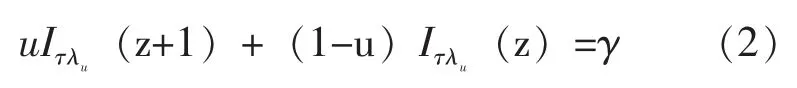
不完全Γ函数的定义为：

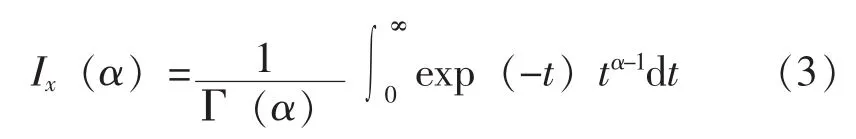
工程上一般取 u=0.5、 γ1=0.8 和 γ2=0.9，进行编程计算，具体的编程计算方法详见参考文献[3]的147页。

b）通过解方程组来确定先验超参数

已知λu1和λu2，并令它们分别等于失效率λ先验分布的γ1和γ2分位数值，即有：

解方程组（4），得到先验超参数c和d的具体数值。

例1 假设在定型试验中用Bayes小样本理论评定导弹上某电子产品的失效率λ，研制试验中获得其有替换定时截尾试验数据（z，τ）=（1，200），且此数据已通过相容性检验，试根据此数据来确定失效率λ先验分布的超参数c和d。

解：

1）取 γ1=0.8、 γ2=0.9，编程求解 λu1和 λu2

当z≥0.5时，式（2）可用下式取代：

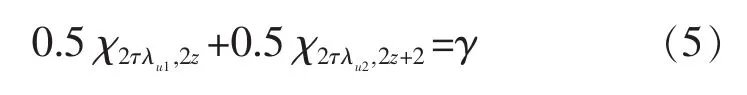
利用Matlab语言，借鉴参考文献[4]147页介绍的方法，围绕式（5）进行编程计算，可得：

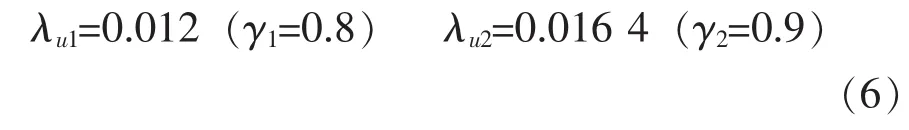
2）解方程组得到c和d

将（6）式代入（4）式可得：

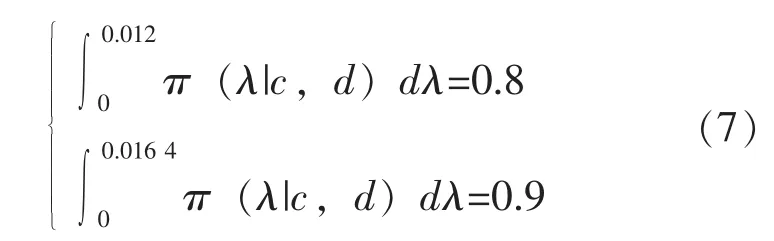
一般不直接求解方程组（7），而用试算法求解，可得 c=1.4，d=1/182，将 c、d值代入式（7），反算可得 γ1=0.8003，γ2=0.9001，γ1和 γ2的绝对误差小于千分之一。

用分位数确定先验超参数的方法同样适用于二项分布参数的先验超参数的确定。

2 专家打分法

专家打分法是根据专家经验或类似产品信息来确定先验分布超参数值。

假设评定导弹单发命中概率指标R，没有研制试验信息，R的先验信息由专家以连续区间形式给出。R的共轭先验分布为β（a，b）分布，其概率密度为[2]：

β分布的均值和方差为：

根据专家经验或类似产品信息，可给出R的先验信息即：R∈（RL，RH）。在确定先验超参数时，首先以均匀分布描述产品的先验信息，即均匀分布的均值和方差为：

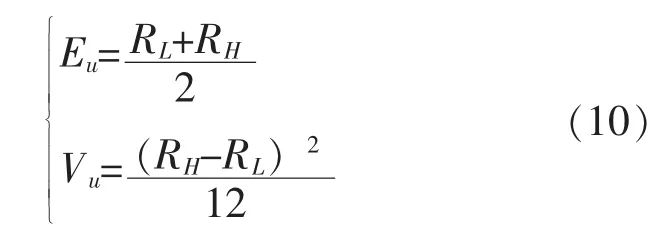
利用一阶矩与二阶矩相等的原理[2]，求出与该均匀分布最接近的β分布作为先验分布，同时求出先验超参数a和b之值，即有：

在实际情况中，解方程组（11）有时得到的是负解，不满足先验超参数非负的要求。这时以先验参数为变量，将均值作为约束，方差作为目标，利用最优化方法求出与该均匀分布最接近的β分布作为先验分布，同时求出先验超参数a和b之值，即有：

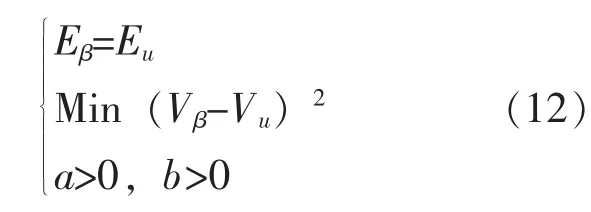
例2假设在导弹鉴定性飞行试验中利用Bayes小样本理论评定导弹单发命中概率R，试验前4位专家给出了R的4组数据，分别为（0.55，0.85）、（0.42，0.82）、（0.53，0.93）和（0.62，0.82），试根据专家数据确定R的先验分布超参数a和b。

解：

1）根据式（13）整理专家数据，确定均匀分布的均值和方差[1]

其中，k为连续区间个数。

将 4组专家数据代入公式（13），可得 EU=0.69，VU=0.02。

2）根据式（11）或式（12）得出先验超参数a和b之值

由公式（11）可得：

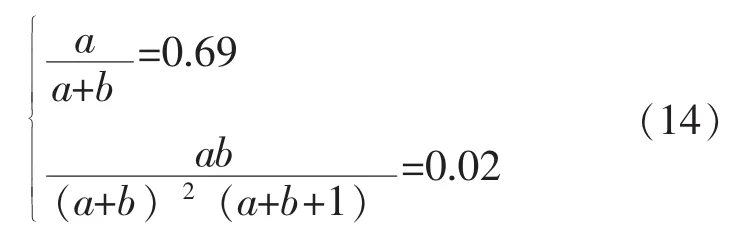
解方程组（14），可得先验超参数a=6.55，b=2.94。

3 结束语

目前有很多确定先验超参数的方法，包括无先验信息可利用时的Box_Tiao方法、Jeffreys方法；有部分信息可利用的最大熵方法；参数经验Bayes方法和非参数经验Bayes方法等。综合比较而言，它们有的不易理解，有的工程上应用很繁琐。本文推荐的两种方法属于参数经验Bayes方法，它们的物理意义较明确，工程上也较容易实现，是两种较好的确定先验超参数的方法。

[1]明志茂，陶俊勇，陈循，等.动态分布参数的贝叶斯可靠性分析[M].北京：国防工业出版社，2011.

[2]周源泉，翁朝曦，可靠性评定[M].北京：科学出版社，1990.

[3]金星，洪延姬.系统可靠性评定方法[M].北京：国防工业出版社，2005.

[4]金星，洪延姬，沈怀英，等.可靠性数据计算及应用[M].北京：国防工业出版社，2003.