坐标转换模型及转换精度影响因素研究
2013-08-13魏生文王山东卓中文
魏生文,王山东,卓中文
(河海大学 地球科学与工程学院,江苏南京210098)
城市建设、交通工程、环境保护等都离不开基础测绘成果的支撑。但目前我国测绘成果主要是1954坐标系、1980西安坐标以及地方独立坐标系下的成果,为了更有效的利用资源,就需要测绘成果在不同坐标系间转换。坐标转换成果的精度与所选择的坐标转换模型、求转换参数公共点个数、公共点空间分布有一定关系。
本文以某地区具有两套坐标的控制点平面坐标为依据,分别用相似变换和仿射变换及不同公共点个数求解转换参数进行坐标转换,分析成果精度之间的差异及规律,得出一些有益的结论[1]。
1 坐标转换模型
从转换模型本身及其参数的含义来讲,转换方法分为两类:一类是考虑坐标系间关系的转换模型,这类模型的参数具有明确的几何意义,或者说坐标系间的关系可用参数表示,如相似变换模型;另一类是数值逼近模型,这类模型的参数和坐标系间的关系无关,转换参数没有明确的几何关系,例如仿射转换模型、多项式拟合模型[2]。
1.1 相似变换
任一点在新坐标系中的坐标为(X,Y),在旧坐标系中对应坐标为(x′,y′),则相似变换的数学模型为
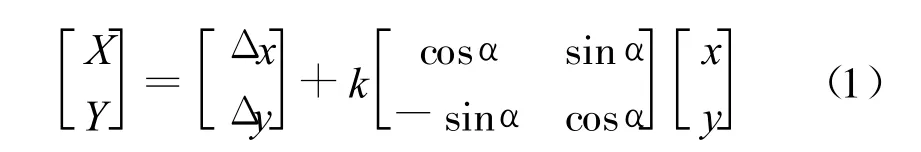
式中:X、Y为原坐标在目标坐标系中的新坐标值;x、y为旧坐标系中坐标点的原坐标值;Δ x、Δ y为新旧坐标系转换平移参数;K为缩放比例;α为旋转角度。
令 d=kcosα,c=ksinα,a= Δ x,b= Δ y ;则式(1)可表示为:
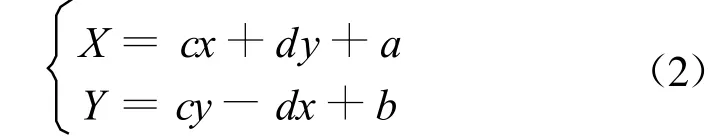
引入误差理论,则式(2)可以变为:
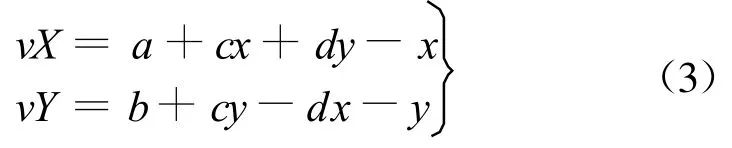
公共点越多,则解算得转换参数精度越高,且公共点分布对解算也有很大影响,公共点分布越均匀,转换精度也相应较高。为解算上式四个未知转换参数,该转换模型至少需要两个以上已知公共点。当公共点个数冗余2个时,采用最小二乘法计算。
假定新旧网中共有n个公共点,建立间接平差误差方程,如式(4)所示。
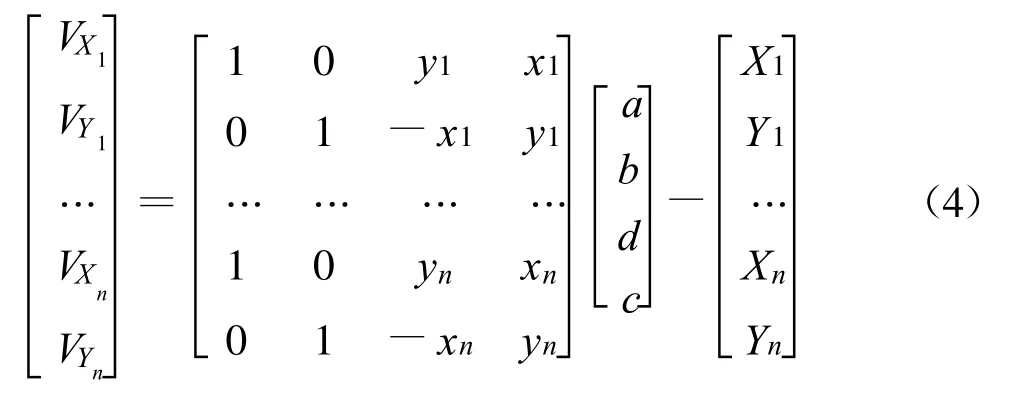
由此可按间接平差原理解算出相似变换模型转换参数的最优解。由上式推导可知,相似转换的过程就是将新坐标系下的元素,经过平移、旋转、缩放后,与原坐标下相配合,保持网形不变的过程。其仅适用于投影方式、椭球元素、椭球定位均相同的情形。优点是转换参数的意义较为明确,计算简便。不足之处在于,该方法只适用于小范围内、局部坐标系间的坐标转换,且没有考虑两坐标系间的局部变形和误差累积,转换精度较低[3]。
1.2 仿射变换
仿射变换数学模型为

式中:a1、b1分别为坐标轴X、Y方向的伸缩比例参数;a2、b2分别为X 、Y 方向的旋转参数;a0、b0分别为x、y方向的平移参数,至少需要3个已知公共点来解算变换参数。
引入平差误差理论,则式(5)可以变为:
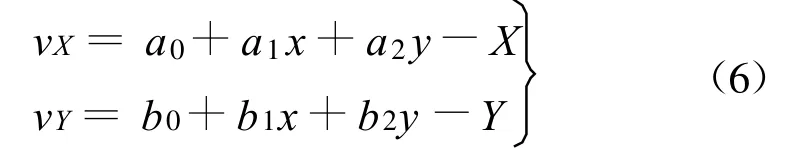
公共点越多,则解算得转换参数精度越高,且公共点分布对解算也有很大影响,公共点分布越均匀,转换精度也相应较高。为解算式(6)中六个未知转换参数,该转换模型至少需要三个以上已知公共点。当公共点个数多余三个时,采用最小二乘法计算。
假定新旧网中共有n个公共点,建立误差方程,如式(7)所示。

由此按间接平差原理可解算出仿射变换模型转换参数的最优解,最大符合转换区域公共点的坐标一致性。仿射转换不具有正形性,其主要特点是:新旧坐标系的点和直线存在一一对应关系,新旧坐标系的任何方向的两段长度比相等,任何三角形面积对比相等[4]。
2 实例计算与分析
在进行坐标转换时,首先需要选取一定的数量的公共点,并利用这些公共点在新、旧两个坐标系中坐标计算该区域的转换模型参数,从而得到适合该区域坐标系转换模型,最后实现两个坐标系的转换。可见公共点的个数以及公共点的位置分布都会影响到最终的转换结果。
以某市主城区北京54坐标与西安80坐标转换为例,已知14个公共点,如表1所示,其点位分布如图1所示,覆盖城区范围400 km2。为了比较不同转换模型的适用范围与转换精度,以及公共点选取的个数与分布对转换精度的影响,做了以下几组实验。
2.1 公共点分布对转换成果精度的影响
公共点个数相同,分布不同。为了验证公共点的分布对坐标转换的影响,分别选取其中的3个点和5个点作为公共点进行实验,考虑位置均匀分布和密集分布的两种情况,设计如下的公共点点位组合,如表2所示。
利用上述组合中的公共点分别进行相似变换、仿射转换、多项式转换模型转换,选取5、10、11、14作为检核点,对比其在各种转换模型中的不同组合的坐标转换差值,结果列于表3、表4。
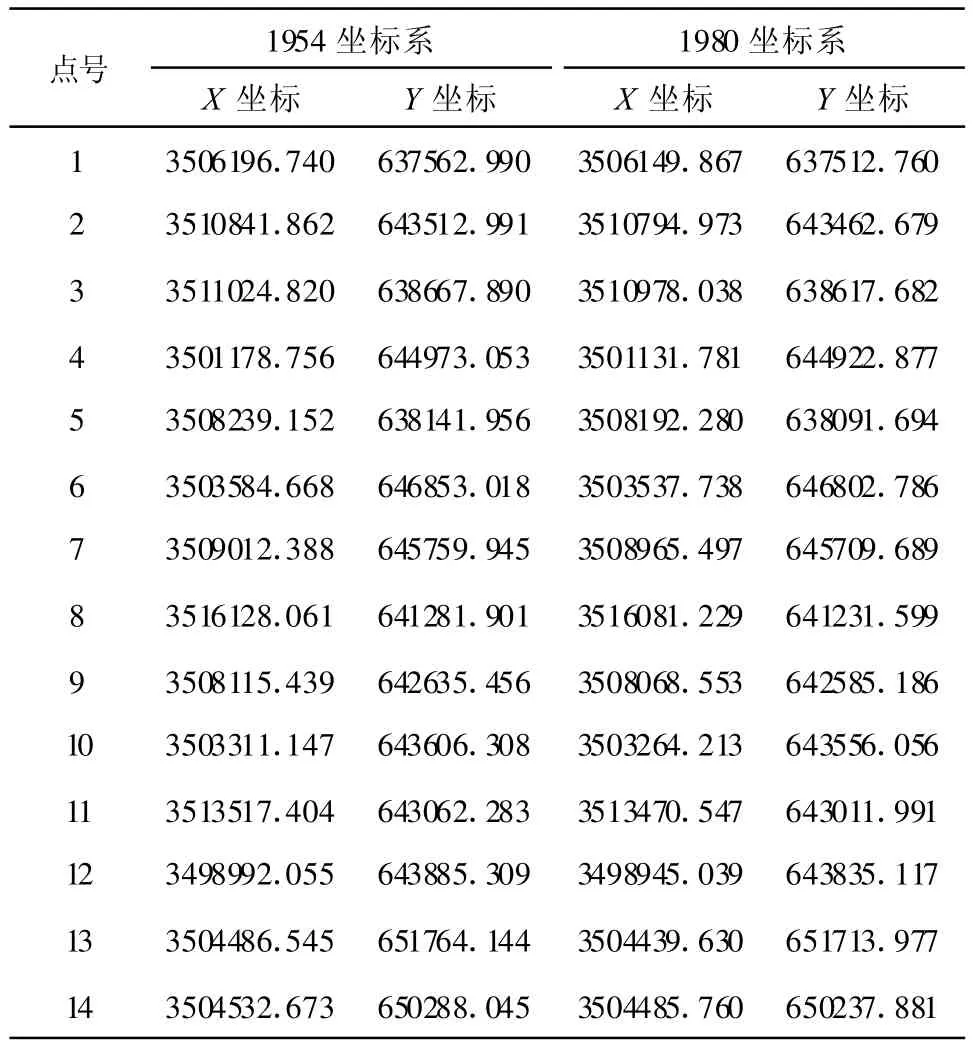
表1 公共点坐标 单位:m
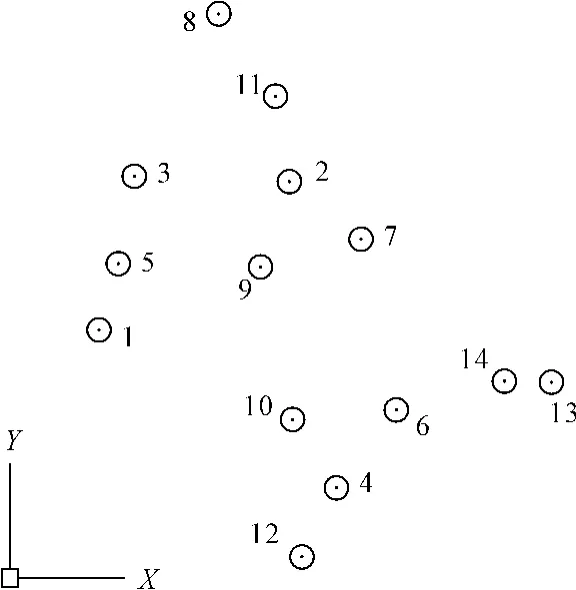
图1 公共点分布图

表2 公共点组合方式
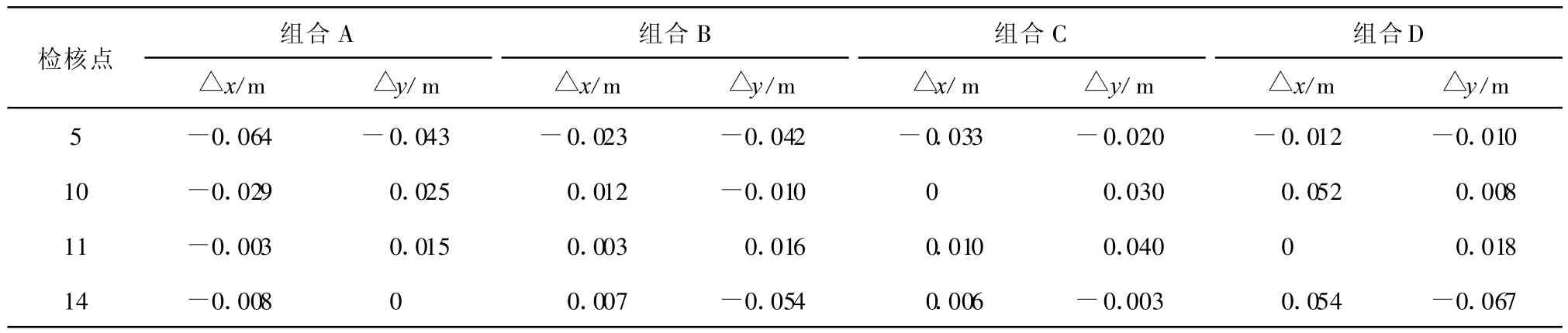
表3 相似变换模型不同组合中平面坐标较差
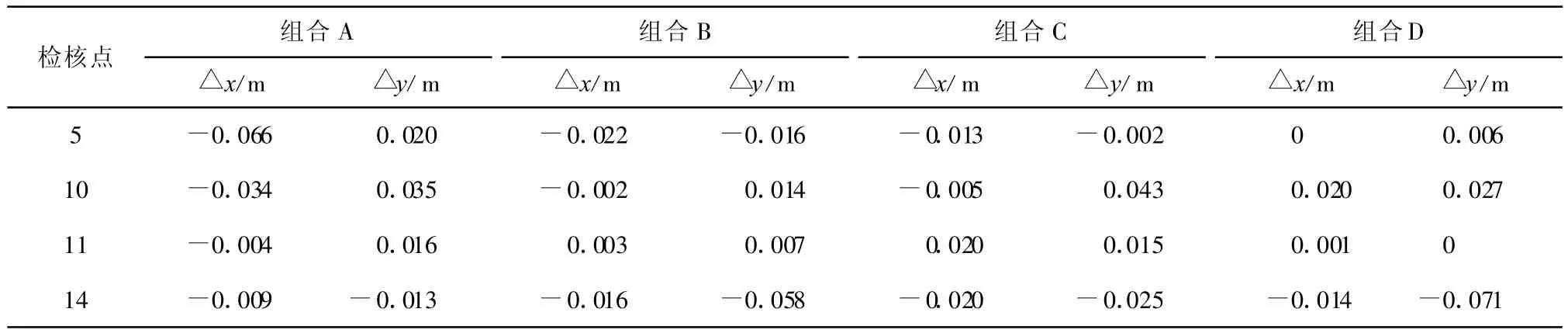
表4 仿射转换模型不同组合中平面坐标较差
在表 3中,A、C组中10、11点均匀分布在区域内,与真值较差较小,14号点因靠近13号点而误差最小,5号点离转换区域中心最远,精度最低。B、D组中,靠近转换区域的5和11号点转换精度相当,10和14号点里转换区域较远,转换精度较低。从A与B组、C与D组转换结果对比,可看出均匀分布在转换区域内时,转换精度较高,离转换区域中心越远,则精度越低。即公共点的均匀分布,可提高坐标转换的精度。
在表4中同样验证了表3的结论,即靠近公共点附近转换精度最高,均匀分布在转换区域内的转换精度几乎一致的,远离转换区域的检核点精度最低。
2.2 公共点个数对转换成果精度的影响
分布均匀,数量不同。分别以相似变换、仿射变换为例,在位置分布均匀的前提下,逐步增加公共点个数,其余点作为检核点检验坐标转换的精度,试验结果如表5、表6、图2所示。
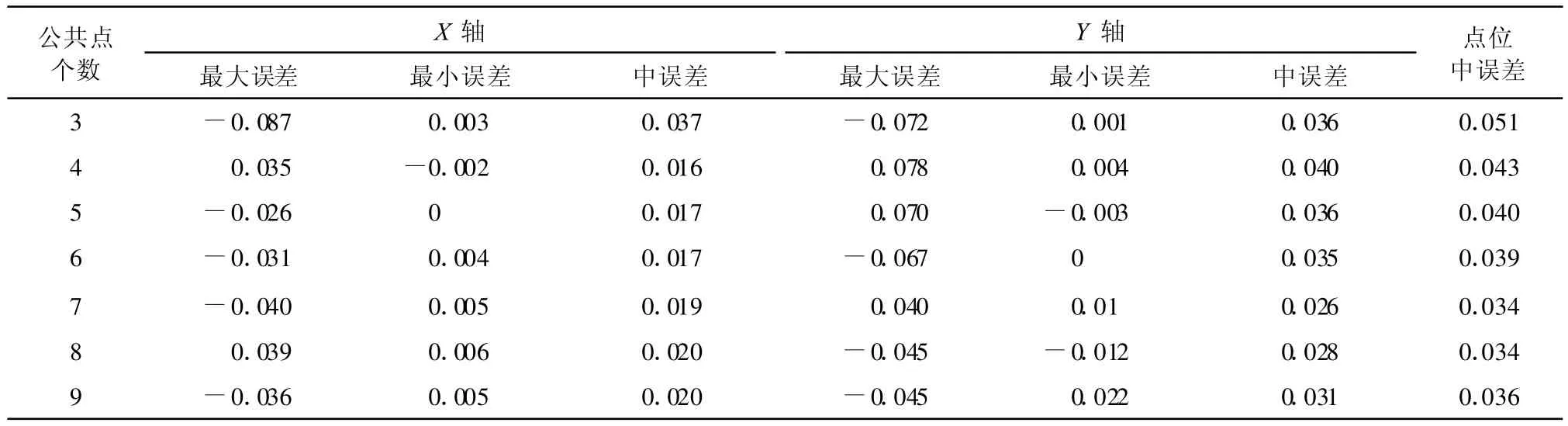
表5 不同个数公共点对相似变换转换成果精度的影响 单位:m
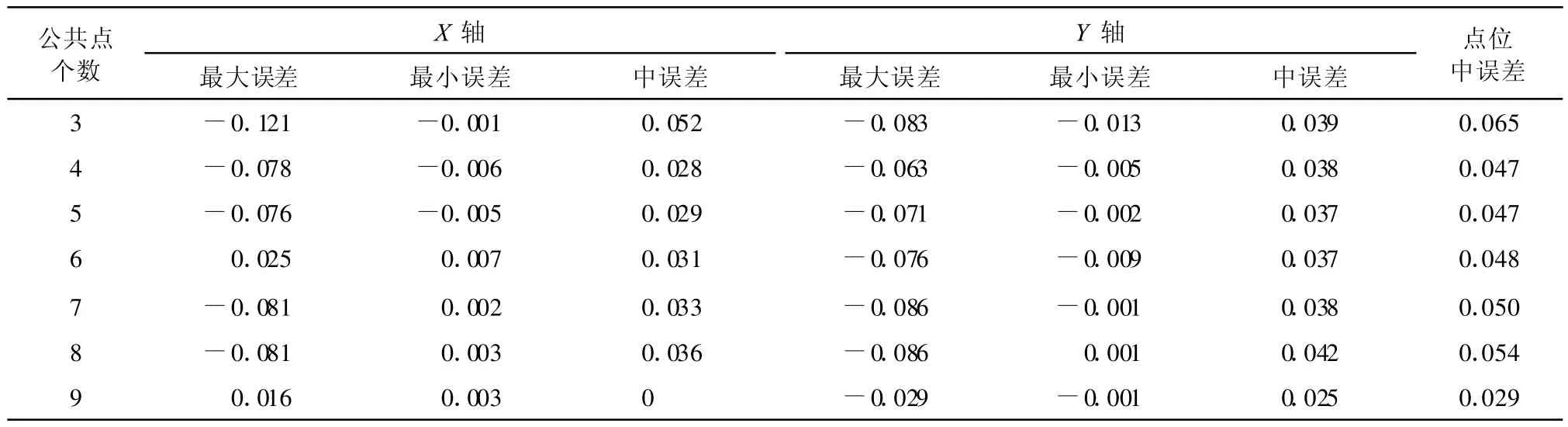
表6 不同个数公共点对仿射变换转换成果精度的影响 单位:m
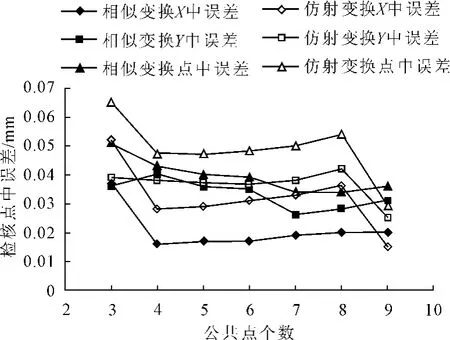
图2 转换成果精度对比
从表5、表6看出,当公共点个数大于四个时,转换成果的精度有了明显提高,当公共点个数达到7~8个时,转换精度达到稳定,相似变换模型中精度从0.051 m提高到0.034 m,仿射变换转换模型的精度也从0.065 m提高到0.05 m,当增加到9个公共点时,转换成果精度达到0.029 m,可能由于含有粗差点所致。
2.3 坐标转换模型对转换成果精度的影响
从表7数据可知,当求解坐标转换参数的公共点个数相同时,采用相似变换和仿射分别进行坐标转换,当公共点个数为3个时,相似变换转换成果的精度明显高于仿射变换转换成果的精度。当公共点个数大于4个时,相似变换转换成果的精度略高于仿射变换转换成果的精度,但差异不明显。
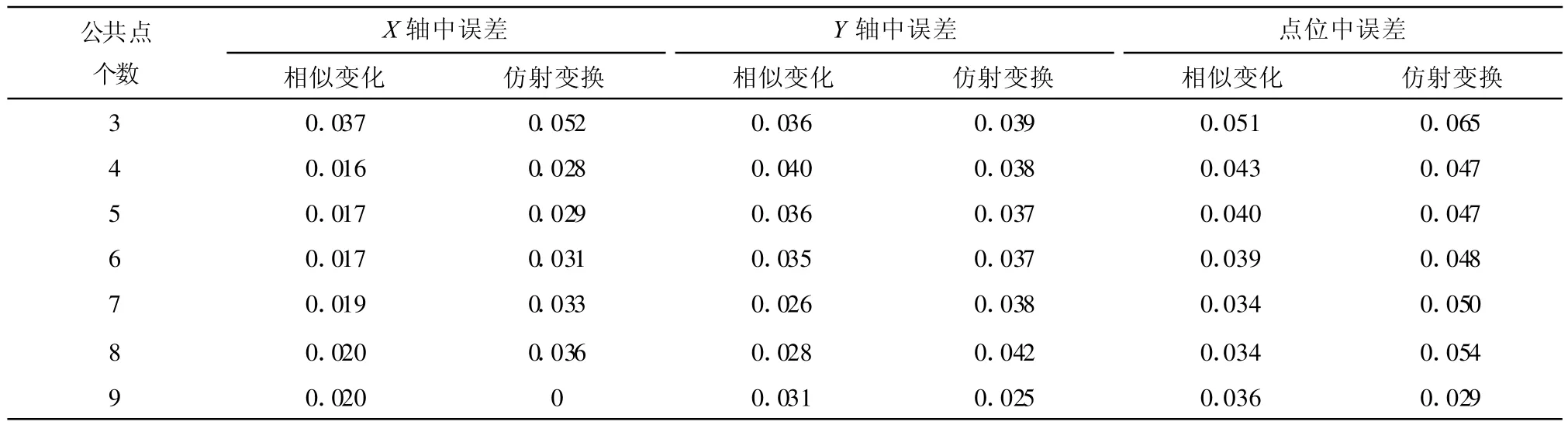
表7 不同转换模型对坐标转换成果精度的影响 单位:m
3 结 论
(1)公共点的分布情况,对坐标转换成果的精度产生很大影响。选取均匀分布的公共点,转换成果的精度较高;反之,则转换精度较低。且离公共点越近,转换成果精度越高。
(2)公共点的个数直接影响转换成果的精度。当选取的公共点个数增加时,转换成果的精度明显提高,当达到一定数量时,转换成果的精度趋向稳定。
(3)在相同个数公共点、相同分布的情况下,相似变换转换模型的转换成果精度相对较高,更适合于小区域坐标转换模型的选择。
[1]赵宝峰,张 雪,蒋廷臣.坐标转换模型及公共点选取对转换成果精度的影响[J].淮海工学院学报,2009,18(4):54-56.
[2]丁士俊,张忠明.几种不同坐标变换方法问题的研究[J].四川测绘 ,2005 ,28(1):16-19.
[3]勾启泰.大地坐标系转换技术与应用研究[D].南京:河海大学,2010.
[4]徐生望,周建国,许 超.坐标转换模型问题研究[J].西部探矿工程,2009,21(2):162-165.
