基于GDS的土体侧向卸荷变形试验研究
2013-08-13胡建林艾英钵
胡建林,艾英钵,陈 宽
(河海大学 岩土工程研究所,江苏 南京210098)
0 前 言
地铁车站基坑的开挖过程实质上是深基坑周边土体的卸荷过程,其变形特性具有独特的规律。然而长期以来,工程人员习惯用常规的加载试验来确定土体参数进行基坑工程的数值分析与设计计算,这必然会产生较大的误差,所以有必要对土体进行卸荷条件下的变形特性进行研究。
国内已有不少学者对土体的卸荷特性进行了研究,何世秀[1]对武汉地区有代表性的粉质粘土进行了K0固结不排水侧向卸荷试验,根据卸荷条件下土体的应力-应变关系得出侧向卸荷条件下的弹性模量表达式。梅国雄[2]利用平面应变仪对土体进行K0固结-侧向卸荷的试验研究,得出侧向卸荷土体的侧向应力-应变关系呈双曲线关系,据此运用邓肯-张建模思路,推导出反应土体侧向卸荷应力路径下的侧向应力-应变关系模型。张艳刚[3]利用真三轴试验仪进行了土体平面应变卸荷应力路径试验模拟,结合有限元强调折减法对实际开挖工程进行了有限元数值模拟。殷德顺[4]参照邓肯-张模型的推导过程,假设土体是各向同性介质,根据增量广义胡克定律,推导出侧向卸荷条件下的切线弹性模量。陈浩[5]利用真三轴仪进行了基坑土体的K0固结侧向卸荷的平面应变试验研究,根据试验得出的应力应变关系运用邓肯-张的建模思想推导出卸荷条件下土体的非线性切线模量表达式。陈善雄[6]进行了K0固结状态下原状粉质粘土卸荷应力路径排水剪三轴试验,采用双曲线函数用平均固结压力将同一应力路径下不同固结压力下的应力-应变关系曲线进行了归一化,并给出了相应的归一化方程。周秋娟[7]针对珠三角洲的典型淤泥质软土进行了室内三轴卸荷试验研究,认为侧向卸荷条件下土体的初始卸荷模量小于轴向加荷条件下的初始加荷模量,并给出了侧向卸荷条件下的变形模量公式。刘国彬[8-9]利用改进的应力路径三轴仪进行了一系列的应力路径卸荷试验,发现卸荷条件下土体的应力-应变关系满足双曲线关系,并利用平均固结压力进行了归一化处理,同时给出了土体的初始卸荷模量与应力路径和平均固结应力之间的关系。王钊[10]根据卸荷试验获得的土体抗剪强度、卸荷条件下的切线弹性模量Et以及卸荷泊松比μt均较加荷条件下的大。
综上所述可知,国内学者对土体的卸荷研究大都是参照邓肯-张模型的推导过程,推导出土体在卸荷时的非线性弹性模型。但邓肯-张模型是以轴向加荷固结排水试验为基础,且认为在加荷过程中(σ1-σ3)-εa关系曲线满足双曲线关系从而推导建立的弹性非线性模型。而土体在卸荷试验中应力-应变关系有时很难满足双曲线关系,这使得邓肯-张模型在土体处于卸荷的情况下很难被应用。所以作者希望可以根据经典的弹塑性模型-修正剑桥模型来建立土体在卸荷时的应力-应变关系模型。
弹塑性模型将荷载作用下所发生的变形分为两部分:一是弹性变形,即可恢复的变形;另一是塑性变形,即不可恢复的变形。1963年英国剑桥大学Roscoe[11]等人根据正常固结土、弱超固结土试样的排水和不排水三轴试样,提出了土体临界状态的概念,并根据能量方程最终推导出剑桥模型。后来Burland[12]等人对剑桥模型进行了修正,提出了在岩土工程中应用广泛的修正剑桥模型。在修正剑桥模型中,对处于屈服状态的土体,如果施加新的应力增量的方向指向屈服面外部,那么新的应力状态到了屈服面的外部,转入新的屈服面上,此时土体将发生弹塑性变形;如果施加的新的应力增量的方向指向屈服面内部,那么新的应力状态即处于弹性状态。修正剑桥模型是一个得到广泛承认和应用的临界状态土力学模型,本文通过在GDS上进行侧向卸荷-排水实验,研究土体在侧向卸荷的条件下的应力-应变状态变化规律,探索在修正剑桥模型的基础上,运用弹塑性理论来解释土体在卸荷状态下的应力-应变关系。
1 试验过程
试验取用南京有代表性的清凉山粉质粘土。该土样的常规物理力学性质见表1。
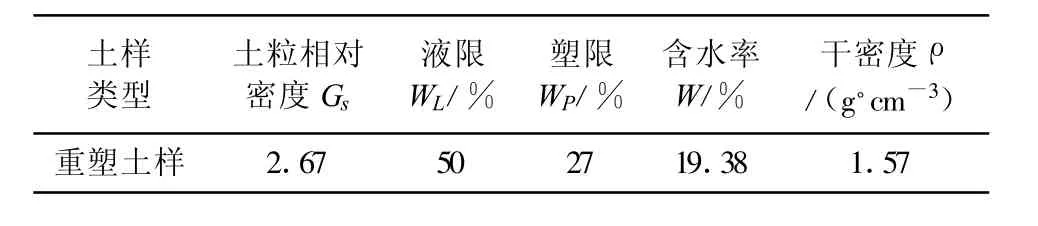
表1 土的基本物理力学性质
1.1 常规三轴试验
为了便于比较,先采用重塑土做了一组等向固结排水的常规三轴试验,其应力-应变关系曲线如图1所示。
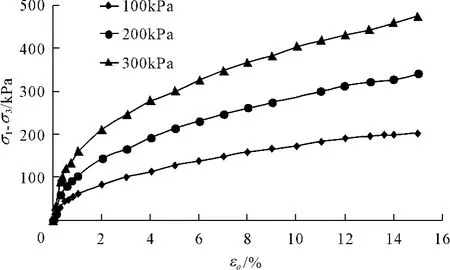
图1 常规三轴试验的应力-应变关系曲线
根据常规三轴试验以及等向卸荷膨胀试验推得修正剑桥模型的参数为:M=0.99,λ=0.106,κ=0.0095,其中 λ,κ值利用不同σ3的等向压缩与膨胀试验绘出v-lnp曲线,曲线的斜率即为 λ,κ的值。M值通过三轴排水剪切或不排水剪切试验,绘出破坏时的p-q图,其斜率就是M。
1.2 侧向卸荷试验
本次试验采用从英国进口的GDS标准应力路径三轴测试系统,与常规三轴仪器对比,该套系统无论从自动化程度、测量精度还是控制方式上都有着后者无法比拟的优势。
GDS三轴测试系统主要由一个三轴压力室、三个计算机控制的液压控制器、一个八通道数据采集板、一个串行接口转换器、一台计算机和若干附件组成。
本次试验采用重塑土样,具体的重塑土样制作方法及试验过程的具体操作按土工试验标准[13](GB/T 50123-1999)的规定进行,重塑土样的控制指标为含水率为19.38%,干密度为1.57 g/cm3,初始孔隙比为0.438。首先让土样在σ3=100 kPa,200 kPa,300 kPa下等向固结,然后在保持轴压不变的情况下,在排水的条件下进行侧向卸荷。所得的(σ1-σ3)-εa的关系曲线如图2所示。
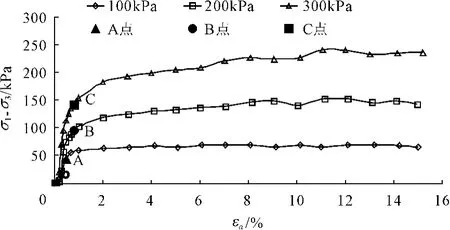
图2 侧向卸荷时(σ1-σ3)-εa关系曲线
可以看出在卸荷的条件下,土体的应力-应变关系分为两个阶段,分别为弹性变形阶段和弹塑性变形阶段。在卸荷的初始阶段(例如围压为100 kPa时的OA段),土体的应力状态尚未达到屈服点时,其应力-应变关系表现为线弹性阶段。当侧向卸荷达到某一状态使得土体的应力状态进入屈服面时,则土体表现为弹塑性阶段,例如围压为100 kPa时偏应力达到A点之后的应力-应变关系。A、B、C点分别为围压为100 kPa,200 kPa,300 kPa时应力-应变关系曲线的拐点,即土体的弹性变形和弹塑性变形的分界点。
2 试验结果分析
根据修正剑桥模型的屈服方程:
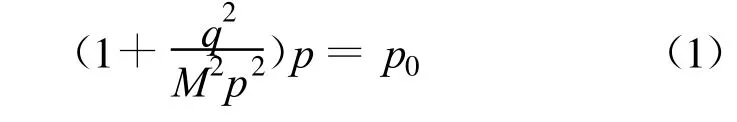
其中M=0.99,p0决定屈服面的大小,在围压为100 kPa、200 kPa、300 kPa时 p0等于围压值 。分别绘出围压为100 kPa、200 kPa、300 kPa时的屈服轨迹和本次侧向卸荷试验的应力路径如图3所示。根据弹塑性理论可知,应力状态点处于屈服面以下是弹性区,当应力状态达到屈服面上,将发生弹塑性变形,任意路径的卸荷回弹均不会引起屈服面的改变。
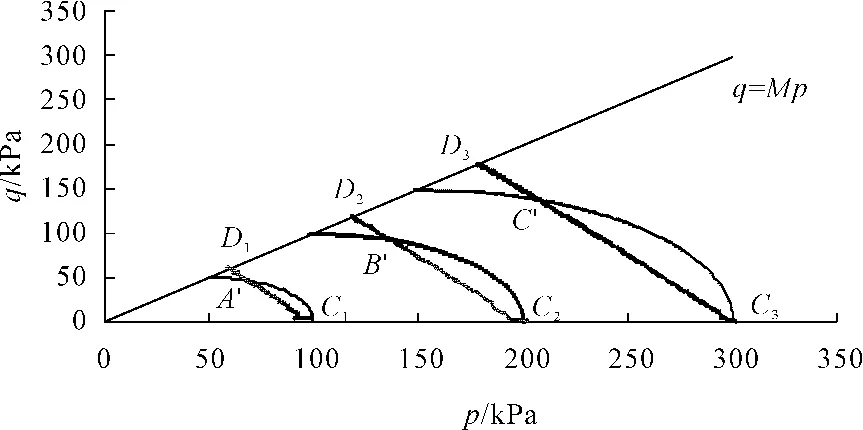
图3 侧向卸荷应力路径与屈服轨迹关系图
因为应力状态处于屈服面以下是弹性区,所以C1A′、C2B′、C3C′均处于弹性区 ,点 A′所对应的偏应力qa=46 kPa。围压为100 kPa的侧向卸荷试验应力应变关系曲线的拐点A所对应的偏应力qA=qA′=46 kPa 。同样可以看出 qB=qB′=93 kPa,qC=qC′=139 kPa。所以可以将轴压不变侧向卸荷的条件下的应力 -应变关系分为线弹性变形阶段和弹塑性变形阶段。
3 本构关系的推导
根据修正剑桥模型的屈服方程,轴压不变侧向卸荷条件下的应力路径为:
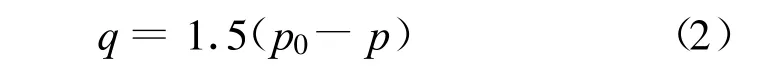
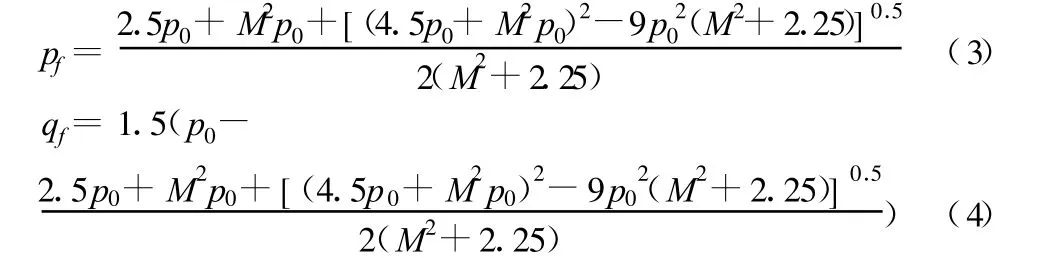
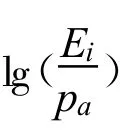
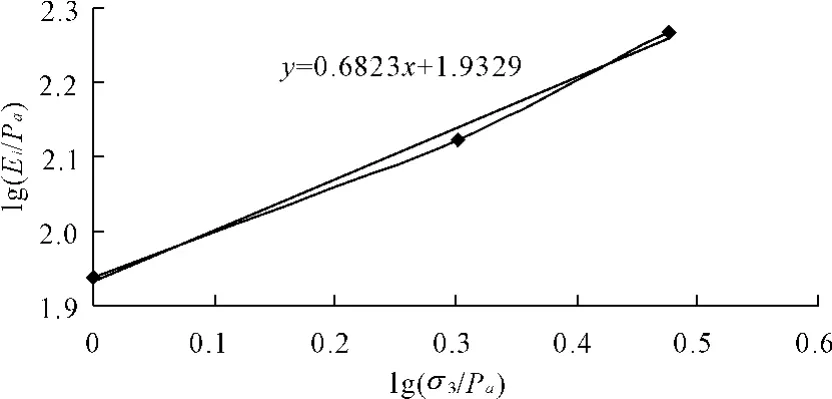
图4 与关系曲线
pa为大气压强。直线的截距为lgK,斜率为n,于是有:
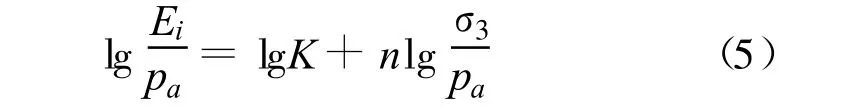
所以当q<qf时土体处于弹性区,其应力-应变关系为:
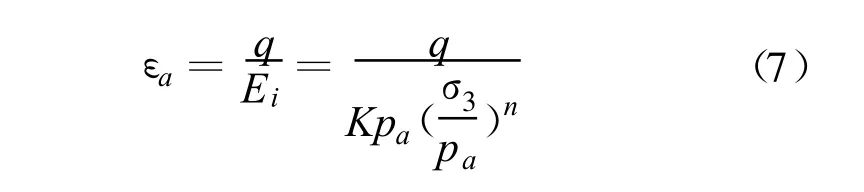
当q>qf时土体进入弹塑性区,其应力-应变关系满足修正剑桥模型的本构关系
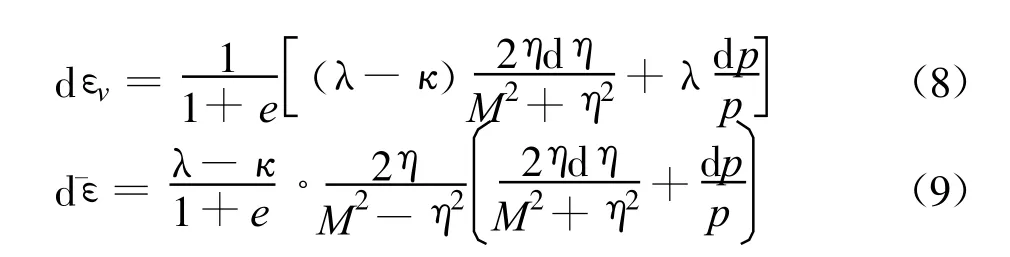
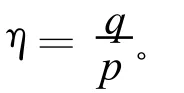

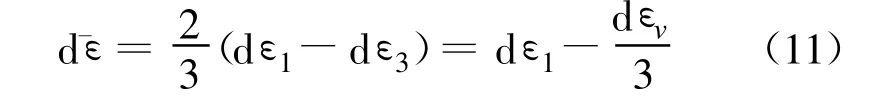
可得:
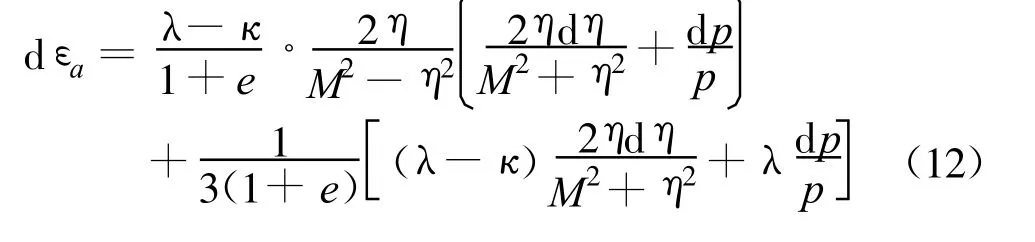
4 模型验证
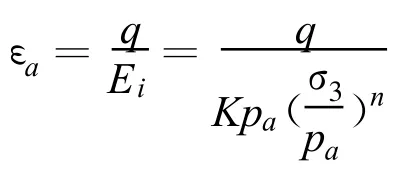
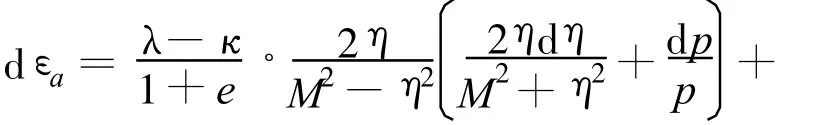
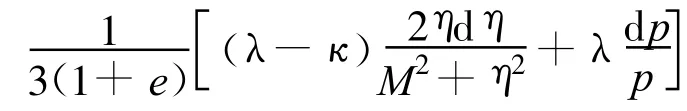
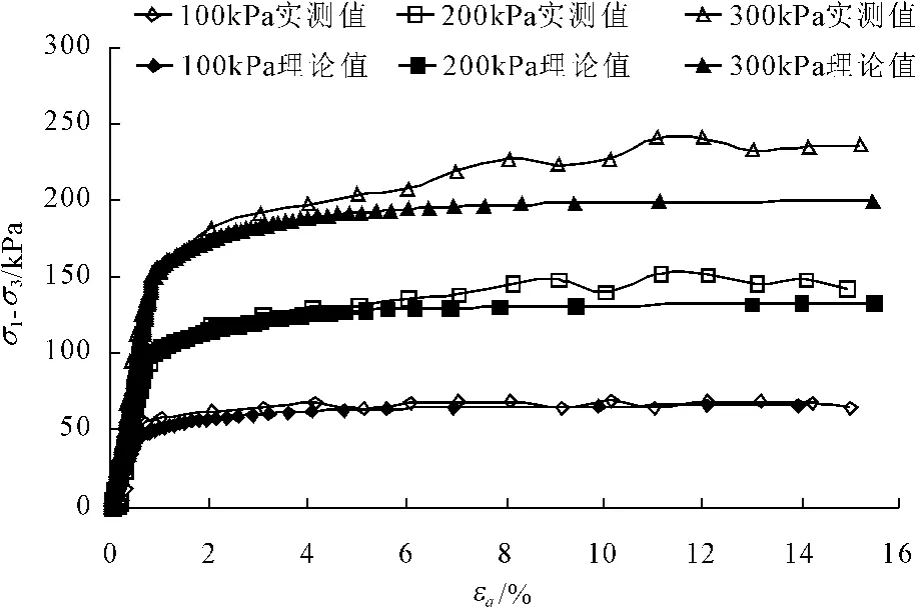
图5 试验数据与模型计算值比较
从图5可以看出理论计算值与试验数据结果基本吻合,初步说明本文推导的模型可以较好的描述轴压不变侧向卸荷时的轴向应力-应变关系特性。
5 结 论
本文运用GDS标准应力路径三轴测试系统对南京地区典型的粉质粘土进行了轴压不变侧向卸荷的排水试验,根据试验结果以及弹塑性理论可知,在侧向卸荷的初始阶段,土体处于弹性变形阶段,当应力状态达到屈服轨迹上时进入塑性变形。因此本文将侧向卸荷下的轴向应力-应变关系分为弹性变形和弹塑性变形两个阶段,并给出相应的应力-应变关系模型。通过试验数据与模型理论计算值的比较表明,推导出的模型能够较好的描述土体侧向卸荷时的应力-应变关系特性。
[1]何世秀,韩高升,庄心善,等.基坑开挖卸荷土体变形的试验研究[J].岩土力学,2003,24(1):17-20.
[2]梅国雄,陈 浩,卢廷浩,等.坑侧土体卸荷的侧向应力-应变关系研究[J].岩石力学与工程学报,2010,29(A01):3108-3112.
[3]张艳刚,张坤勇,史峤臻.开挖卸荷土体本构模型研究方法[J].水利与建筑工程学报,2010,8(4):40-43.
[4]殷德顺,王保田,王云涛.不同应力路径下的邓肯-张模型模量公式[J].岩土工程学报,2007,29(9):1380-1385.
[5]陈 浩,梅国雄,李 治.基坑土体侧向卸荷条件下的变形性状研究[J].合肥工业大学学报,2009,32(10):1551-1553,1570.
[6]陈善雄,凌平平,何世秀,等.粉质黏土卸荷变形特性试验研究[J].岩土力学,2007,28(12):2534-2538.
[7]周秋娟,陈晓平.侧向卸荷条件下软土典型力学特性试验研究[J].岩石力学与工程学报,2009,28(11):2215-2221.
[8]刘国彬,侯学渊.软土的卸荷模量[J].岩土工程学报,1996,18(6):18-23.
[9]刘国彬,侯学渊.软土的卸荷应力-应变特性[J].地下工程与隧道 ,1997,(2):16-23.
[10]王 钊,黄 杰,咸付生,等.土的卸载试验和在万家寨引水隧洞变形分析中的应用[J].岩土工程学报,2002,24(4):525-527.
[11]Roscoe K H,Schofield A N,Thurairajoh A.Yielding of clays in stateswetter than critical[J].Geotechnique,1963,13(3):211-240.
[12]Roscoe K H,Burland J B.On the generalized stress-strain behaviour of‘wet'clay[C]//Engineering plasticity.Cambridge:Cambridge University Press,1968:535-609.
[13]国家质量技术监督局.中华人民共和国建设部.GB/T50123-1999.土工试验标准[S].北京:中国计划出版社,1999.
