整型2D－IDCT算法的优化与实现

胡小涛，梁利平

(中国科学院微电子研究所，北京 100029)

自从Ahmed和Rao于1974年给出离散余弦变换(DCT)定义以来，这类变换被广泛应用，对于这类变换的快速算法的研究发展也十分重要，特别是对特定条件下的快速算法的研究对于整个系统的性能提高有很大帮助。

在IDCT计算中，对于一个8×8大小的图像块而言，如果要直接计算，将需要4096次乘法和4032次加法。而IDCT的3种经典快速算法为B.G.Lee算法、AAN算法和LLM算法，都是基于如何减少运算次数而设计。而对于整数2D-IDCT变换而言，如何保证计算精度满足IEEE Standard 1180—1990与离散余弦变换标准也是一大挑战。

本文基于自身的DSP平台，通过不同算法之间的比较与分析，设计出满足标准前提下的解决方案，设计并确保计算精度，在此算法基础上进行汇编优化，尽可能地减少消耗，得到满足预期的实现结果。

1 整型2D-IDCT算法设计

1.1 算法描述

为了下一步的算法设计，本文首先对公式进行简单变换

把公式转换为矩阵并经过余弦函数化解得到

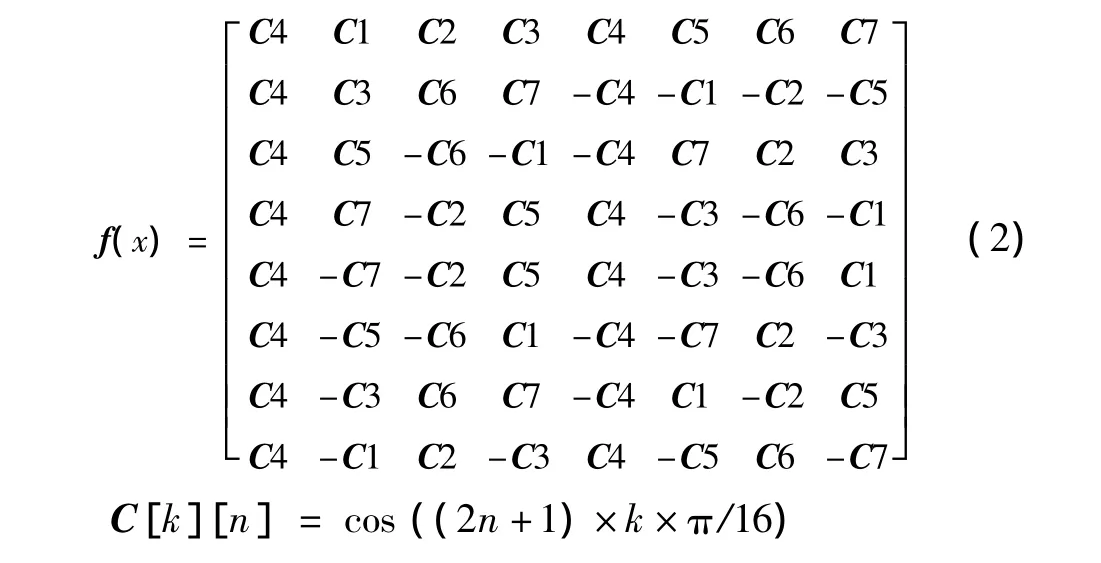
于是可采取常用的蝶形运算方法(Loeffler，Chen W等IDCT快速算法)，过程如下

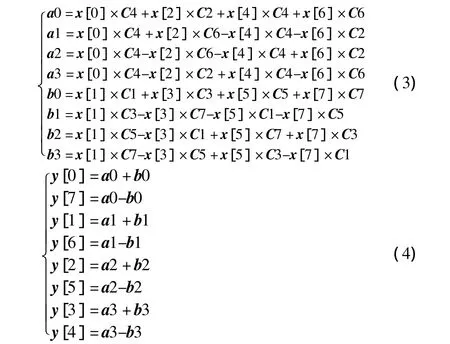
计算后的y［0］～y［7］作为输入再次运算便可得到2D-IDCT 结果［1-3］。

1.2 算法设计

进行整数IDCT变换［4-6］，需将上述公式中矩阵C(泛指)中的浮点运算定点化，因此如何最大限度保证数据精确性成为这一步的首要工作。在已有的蝶形运算优化的基础上，本文根据精度标准需求，提出保证精度的解决方案，在保证数据精确性的前提下实现优化。

由于扩展时会进行一次舍入，因此第一次运算的扩展位数应该达到最大限度。而转换成2次1D-IDCT运算后，第一次运算结果为32位，进入第二次计算时需要缩小到16位参与运算，必须舍弃低位数据来参与第二次运算。

本文暂且遵循这样一个原则:尽量保留第二次运算前输入数据位数。本文在后面会对比矩阵C与保留位数之间的优劣。

第一次IDCT运算的输入是16位数据，实际有效位数为12位整数(-2048～2047)。运算中共有8个数据参与加减，须空余3位缓冲区域，故而最大可用于矩阵C位数为17位。而根据上面得到的第二次运算输入数据保留最多的原则。第二次矩阵运算时输入数据要保留16位。同样会进行8个数据加减占用3位，因此第二次的运算中矩阵C的可设定位数为13位，参考图1。

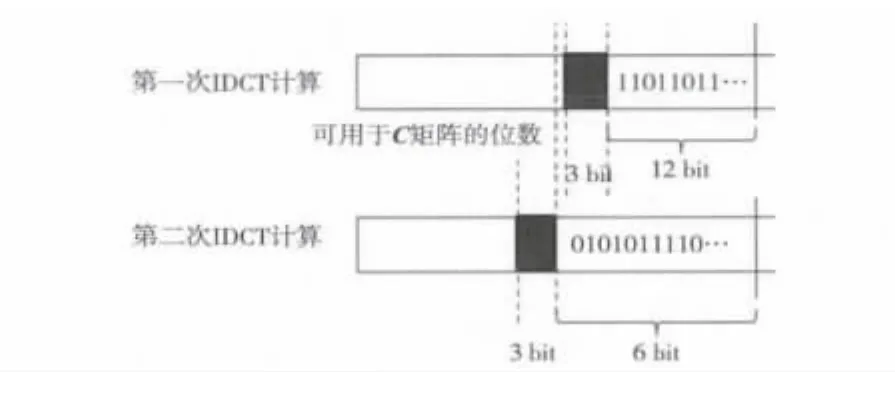
图1 矩阵C参考

于是有两种方案选择:

1)方案1，固定选取矩阵C为13位，参与2次矩阵运算。

2)方案2，第一次选择17位矩阵C，第二次选择13位，分别运算。

如果2次选择的矩阵相同，后面实现起来将会更加简洁;但如果精度不能满足要求，则需要采取方案2。但经过考虑认为，每次二维IDCT计算都要使用2个矩阵来进行，损耗太大。特别是在汇编实现时，每次IDCT运算的第一次计算结果缓存之后，还需要更新一次矩阵C，不仅会导致寄存器紧张，而且耗时较多。

实际操作中发现每一步蝶形运算中y［0］=a0+b0=(x［0］× C4+x［2］× C2+x［4］× C4+x［6］× C6)+(x［1］×C1+x［3］×C3+x［5］×C5+x［7］×C7)，未能饱和利用数据位。cos(n×π/16)是0.195～0.98之间的。这样就算是输入比特流x［0］到x［7］都为12位数(比如2000以上的数据)，相加之后的 y［0］只有4.577×2000，而预留的3位总共能达到8×2000大小的数据。于是在矩阵C中乘，因为 4.577×≈6.47，没有超过8。同样的2个矩阵C相乘之后相当于=2，这样在之后的右移移位还原中多移一位即可，不用再做额外的变换。

于是，提出方案3:选取固定的13位矩阵再乘作为矩阵C参与运算。

3种方案实验结果对比参见表1，颜色加深处表示结果未达标。

IEEE Standard 1180—1990标准主要要求有:

1)经过浮点运算得到参考结果f’(x，y)与整数IDCT运算结果f(x，y)误差值不大于1。

表1 3种方案实验结果对比

2)下面4个误差不越界:

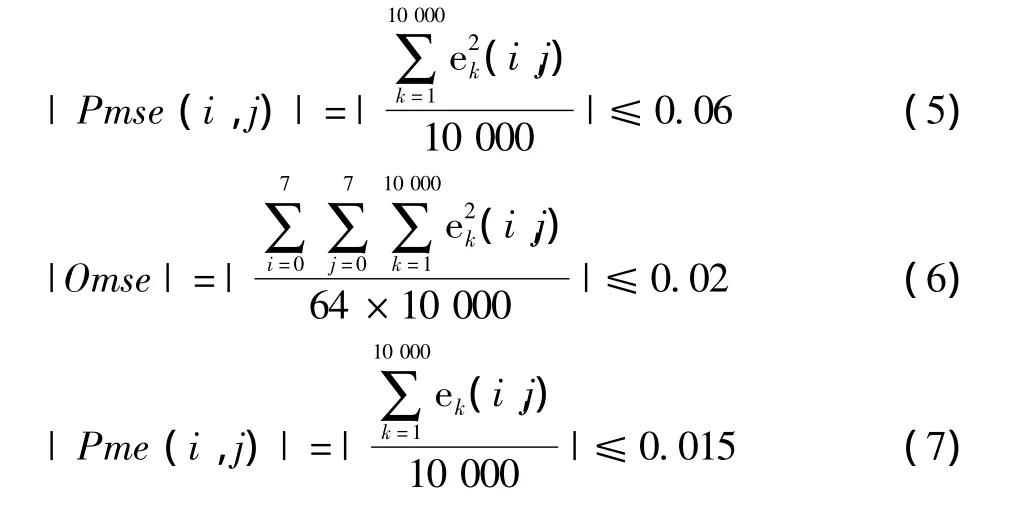
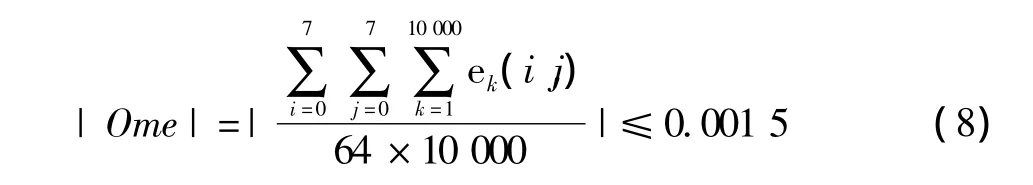
本文选择方案3进行测试。精度远远超过IEEE Standard 1180—1990标准的要求。与参考文献［7］中针对精度提升的离散余弦变换的测试精度相仿，其中在体现整体性能的Pme(点平均误差)参数上本文精度要优于文献［7］。

在大幅度满足精度要求的基础上，继续进行标准离散余弦变换要求测试，在［-5，5］，［-256，255］，［-384，383］这3个区间段之间随机抽取1×104和1×106两组数据参与测试，结果参照表2，阴影部分为文献［7］中经过精度优化后的整体性能参数对比。

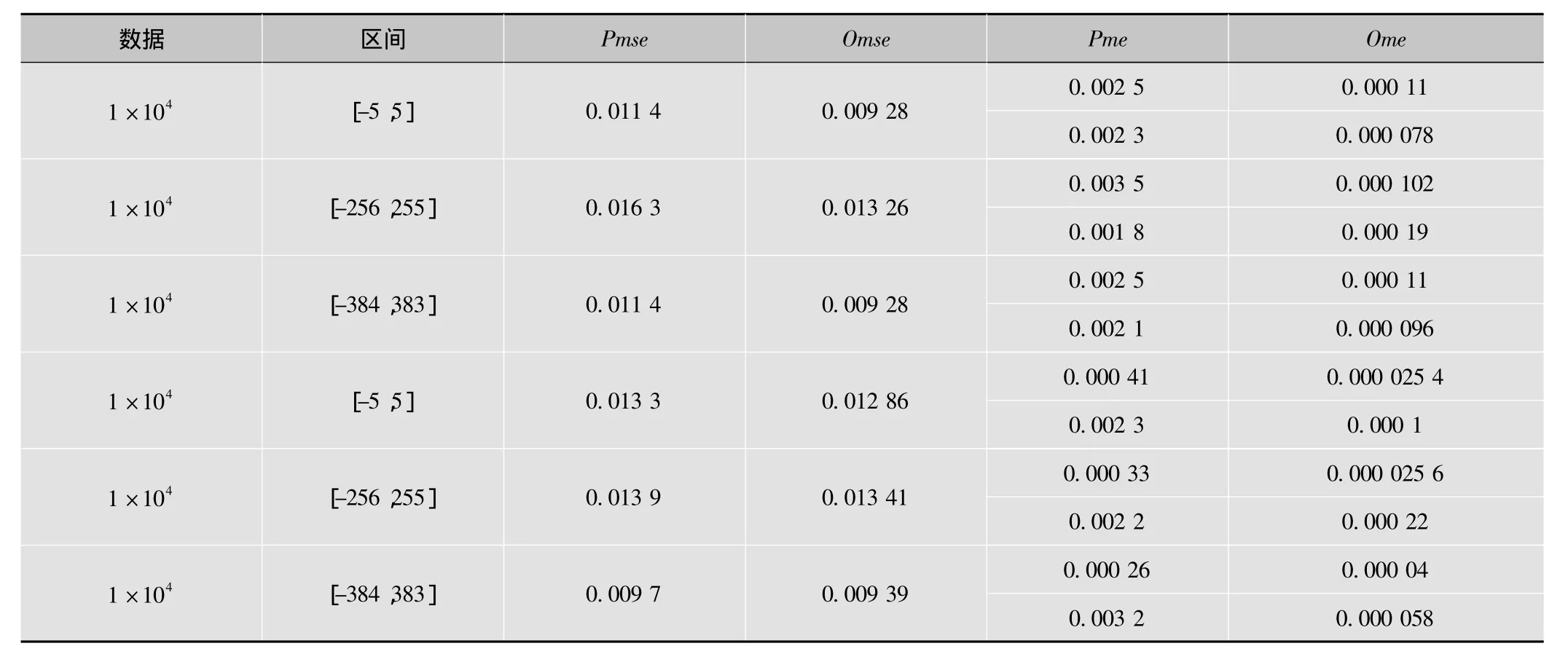
表2 标准离散余弦变换测试结果

由于本文之前遵循一个原则:尽量保留第二次运算前输入数据位数。实际上如果减小第二次运算的保留位数，可以得到更精确的矩阵C。本文将保留位数与矩阵C大小的不同设定得到一个误差对比，参数去除了相同的分母，保留分子误差数据，结果见表3。

表3 矩阵C大小不同设定的误差对比

由测试数据可以得知，选择更大的矩阵C将使得Omse测试参数更小，选择保留更多位数将使Ome测试参数更小。这是因为两种选择方式降低失真度的重点不同，实现者可以通过实际操作的需要有所取舍。在本次实现中两者均能达到测试标准，最后本文采取优先保留位数的方法。

1.3 汇编设计

本文在自主设计的指令集环境下完成上述IDCT运算模块，有包括MIPS 32个寄存器在内一共64个32位寄存器可供支配。由于IDCT运算中间结果为64个，在要求高并行度计算的前提下，无法提供足够寄存器空间存储中间数据，第一次IDCT计算结果将会回存并在第二次计算时再取出。实现流程如图2所示。

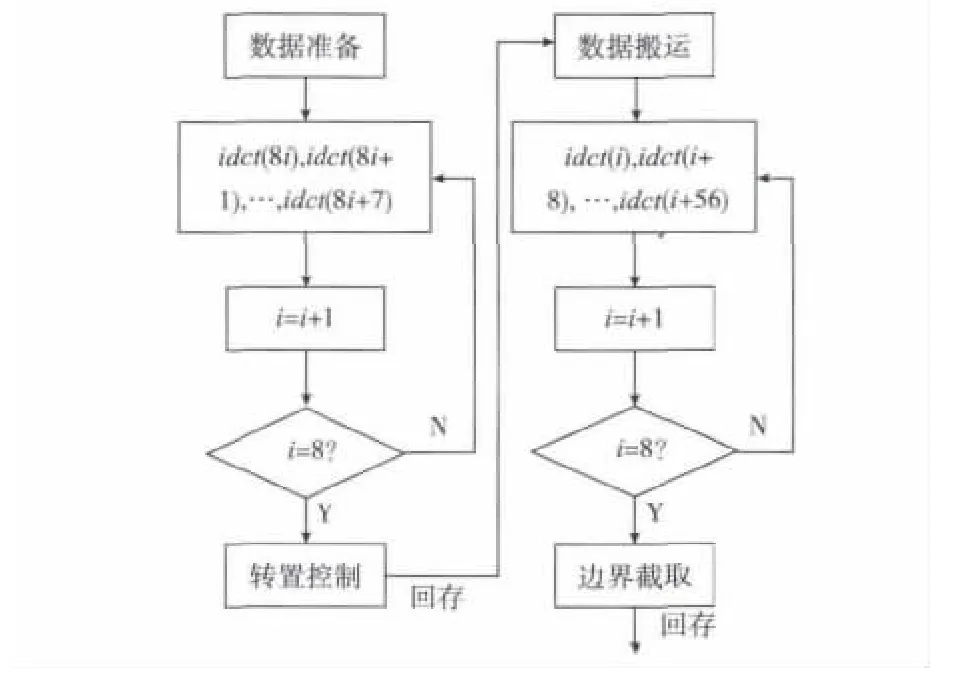
图2 汇编实现流程

由上述流程图可知，2次8×8运算、转置、数据搬运、边界截取组成了一次IDCT计算的消耗主体，同时也是优化重点。

指令环境对于每次转置运算，针对的是4×8的数据块，转置之后的数据参与第二次运算后要存在寄存器中然后顺序存回内存。在汇编中转置消耗较多，开销主要在转置后的数据调整和第二次运算后为后面边界截取进行数据准备，本文经过分析转置消耗，采取手动配置初始寄存器位置的方式将最终转置控制消耗降低为2个周期。配置如图3所示。

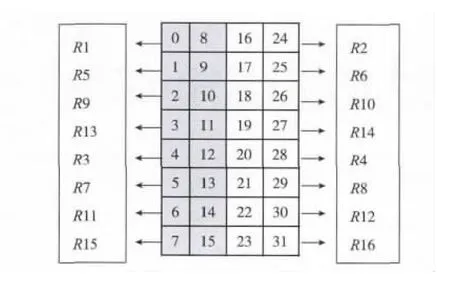
图3 转置运算寄存器分配

在每个4×8计算块的数据并行性保证上，采用多指针电梯式扫描方式存取，将数据的转移搬运冗余操作降低到最低限度。经过每次电梯式扫描方式存取之后，4×8数据块运算完毕，进入下一个模块计算时横向移动即可，这样既保证了数据的流水线操作，大大降低了损耗，同时也化简了两次运算中数据搬运的冗余操作。操作如图4所示。

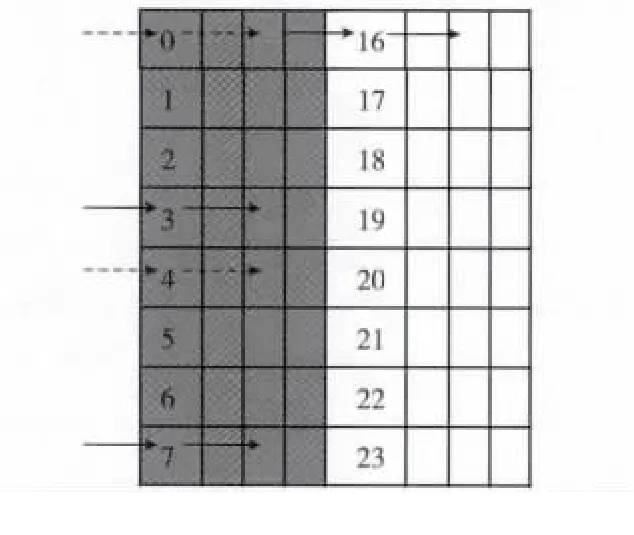
图4 电梯扫描方式操作

在流程图中可知，每次IDCT运算需要循环8次，而在上述的汇编优化中可知，为实现并行运算和优化方法，需要将每次运算的循环数减小，增加循环体内部计算。为找到最佳循环次数，本文在操作中将循环次数逐渐减小，并对每个循环次数下的结构进行尽可能的优化仿真，得到对比数据见表4，阴影处表示选择此方法。

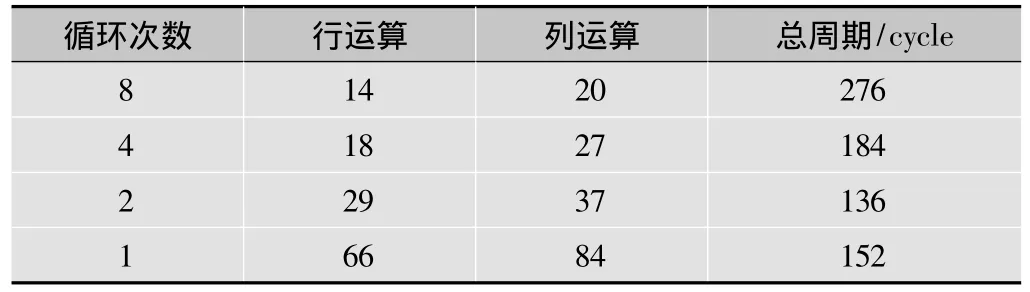
表4 循环次数选择与周期损耗关系

从上面对比图可以得知，随着循环次数减小，行运算和列运算中每次循环的开销变大，但综合来说循环2次时总周期最小，最终优化结果需要(6×136+8)个周期(在6 blocks的情况下)。完全去除循环时，虽然减少了循环消耗，但增加了寄存器分配操作，且流水线利用率也已达到饱和，最终效率不及前者。于是采用2次循环方法。

2次循环方法最大限度地利用了之前的转置控制寄存器分配和边界截取时的并行处理能力，最大限度地发挥了流水线作用，使得最终的消耗在140以内。

2 实验对比

纯MIPS指令实现的计算如果不加优化，对于每次IDCT计算会进行4096次乘法和4032次加法，在仿真器下做一次计算，周期数接近20000。而采用快速算法优化之后用MIPS指令自动实现汇编进行一次IDCT计算周期数在1000左右，作为本文性能指标的纵向比较。

同时，本文参考了TI产品指标中的IDCT模块消耗作为参照标准，这些数据是在TI平台上优化之后得到的，采用的指令系统、算法和优化方法与本文不同，作为性能的横向比较(见表5)。

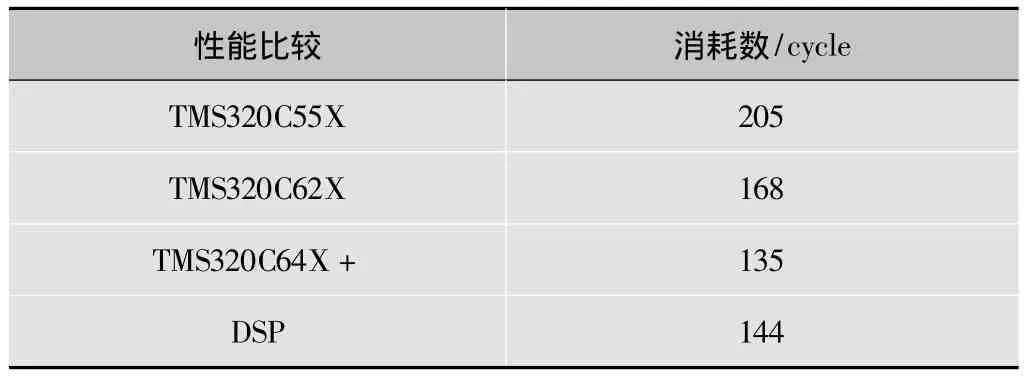
表5 IDCT模块性能对比表

在运行多个block下，各个不同产品性能指标有一定变化，DSP在6 blocks下周期数可到137，参照视图见图5。

图5 IDCT模块性能对比图

经过分析，本文基于的DSP平台下的IDCT计算效果好于TMS320C62X，差于TMS320C64X+系列。TMS320C64X+解第1个block的周期为135 cycles，在解到6 blocks之后速度会提升到103 cycle。这也是需要学习和改进的地方。

3 结束语

本文依据离散余弦变换和IEEE Standard 1180—1990标准分析并选择符合要求的算法来实现2D-IDCT功能，所进行的验证试验符合预期。在汇编优化上针对本文所基于的DSP指令设计符合需要的相应代码并使用并行流水线结构优化，实现了IDCT运算并达到计算优化度预期。在与同类IDCT运算方法进行结果比较之后也找到了一些不足，这也是下一步需要优化的方向。

［1］CHEN W H.A fast computational algorithm for the discrete cosine transform［J］.IEEE Trans.Communication，1977，25(9):1004-1009.

［2］FEIG E，WINOGRAD S.On the multiplicative complexity of discretecosine transform［J］.IEEE Trans.Inform.Theory，1992，38(6):1387-1391.

［3］LOEFFLER C，LIGHTENBERG A，MOSCHYTZ G S.Practical fast 1-DDCT algorithms with 11-Multiplications［EB/OL］.［2013-01-20］.http://ieeexplore.ieee.org/xpl/articleDetails.jsp reload=true&arnumber=266596.

［4］SLAWECKI D，LI W.DCT/IDCT processor design for high data rate image coding［J］.IEEE Trans.Circuits System Video Technology，1992，2(2):135-145.

［5］EI M，BELKOUCH S.An efficient pipelined fast and multiplier-less 2-D IDCT for image/video decoding［EB/OL］.［2013-01-20］.http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5945687.

［6］KIHO C，KIHOON L.Zero coefficient-aware fast IQ-IDCT algorithm［EB/OL］.［2013-01-20］.http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=5657972&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D5657972.

［7］唐永亮.高速高精度离散余弦变换的设计与实现［D］.天津:天津大学，2008.