基于修正剑桥渗流耦合模型的闸室有限元分析

2013-08-13何良德苏兴海徐笛清夏正东魏东

中国港湾建设 2013年3期

何良德，苏兴海，徐笛清，夏正东，魏东

（1.河海大学港口海岸与近海工程学院，江苏南京 210098；2.江苏省扬州市航道管理处，江苏扬州 225003）

0 引言

船闸闸室是一种先开挖基坑，再浇筑底板与闸墙，最后两侧回填的半埋入式结构。以艾伦港船闸[1]为例，船闸基坑深度为17.37 m，实测回弹量在中心线处为8.8 cm，在坡脚处为7.9 cm；船闸完建充水前实测沉降量为5.8 cm，小于实测回弹量。前苏联在开挖船闸基坑（深10 m左右）和降低地下水位的同时，观测到坑底面升高10 cm以上。因此，回弹再压缩量问题在船闸工程中不容忽视。

目前，船闸沉降计算常采用考虑闸基深开挖卸载回弹效应的e-lg p曲线的分层总和法[2]，在底板内力计算时常用文克尔地基、半无限或有限深弹性地基[3]等模型，便于查表计算。但何良德等[4]研究表明，分缝施工的中底板与墩墙相比，其基底压力明显减小，浅部地基土始终处于回弹-再压缩状态，在合缝至完建期，底板下地基刚度呈现中部大、两侧小的特征。因此，如果不考虑回弹再压缩模量的影响，计算的底板沉降偏大，计算的正弯矩偏大或者负弯矩偏小。

在施工期，导致闸墙倾斜的主要作用有结构上荷载（自重、土压力）和回填边载等。重力式闸墙结构自重通常向内侧偏心，加上墙后土压力作用，闸墙呈前倾向趋势。但多数船闸在回填土边载作用下，闸室墙是后倾的，有的甚至引发了事故。船闸设计规范[5]考虑到砂性土、黏性土地基固结的不同特点，为安全计，从可能的最不利情况出发，边载采用两个极限值，但规定的取值范围大，实际计算时较难把握。

另外，基坑开挖后，地基土应力不会立即得到释放，基底回弹不会马上完成，原地面以下、以上填土的边荷载效应存在差异，这些问题对船闸结构位移、变形、内力的影响尚未得到充分考虑[6]。目前，有限元仿真分析技术在船闸设计中应用越来越广泛，周清华等[7]、冯大江[8]采用Biot固结模型和邓肯-张模型（Duncan-Chang model）或D-P模型（Drucker-Prager model）耦合方法分析了闸首结构。D-P模型考虑了中主应力σ2′影响，但只有弹性模量的算式，不能直接应用于回弹再压缩问题的分析；邓肯-张模型给出了回弹模量的算式，却忽略了中主应力σ2′影响，不能较好反映基坑开挖卸荷、闸墙浇筑再加荷时不同应力路径的应力–应变关系。

修正剑桥模型（modified Cam-clay model）[9-10]避免了上述两种模型的缺点，较好地阐明了土体在正常固结和回弹再压缩时弹塑性变形特性，是应用最为广泛的软土本构模型之一。本文结合邵伯三线船闸工程，利用ABAQUS软件，基于修正剑桥与渗流固结耦合模型，分析基坑开挖对闸墙位移的影响，研究闸墙倾斜度发展规律，提出倾斜预留量，确保闸室施工尺度满足验收标准[11]和通航安全的需要。

1 基本理论介绍

1.1 渗流固结模型

在荷载作用下，水从土孔隙中挤出，孔隙压力降低，有效应力增加，土体逐渐压缩，最后达到稳定的固结过程，是一种流体-固体的相互作用（流固耦合）的现象。比奥（Biot）从固结机理出发，较严格地推导了孔隙压力消散与土骨架变形相互关系的三维固结方程[12]：

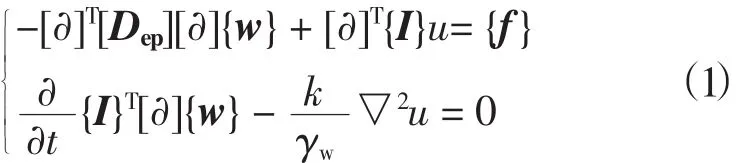
式中： [∂]为偏微分算子；▽2为拉普拉斯算子；{w}= [wx，wy，wz]T为位移分量；u为超孔隙压力； [Dep]为弹塑性矩阵； {I}为单位矩阵；k为土的渗透系数；γw为水体重度； {f}为外荷载列阵。

式（1）第一式为平衡方程，包含3个偏微分方程，第一项表示发生的位移所对应的力，第二项表示当前的孔压所对应的力，它们的和与外荷载平衡。第二式为连续性方程，第一项表示单位时间内位移改变所对应的体积变形，第二项表示孔压变化所引起的渗出水量。力的平衡中有孔压的贡献，水量平衡中又有变形的贡献，相互耦合。

1.2 修正剑桥模型

在p-q面上，修正剑桥模型的屈服面为椭圆，屈服面函数由下式表示：

式中：σ1′、σ2′、σ3′为有效主应力；p 为有效平均应力；q为广义剪应力；pc为先期固结压力，它控制了屈服面的大小；M为所有排水和不排水剪切试验时破坏点在p-q面上投影形成的临界状态线（CSL线）的斜率，简称应力比。CSL线的一个重要特征是它与屈服面的交点是剪应力达到最大值的点。

试验表明υ、p和q三个变量存在着唯一性关系（υ为比容，υ=1+e；e为孔隙比），因而在υ-p-q三维空间中形成一个曲面，该曲面称为状态边界面。式（2）中pc是变量，隐含了硬化的含义，可取塑性体积应变为硬化参数，将pc表示成的函数，最后得屈服方程：

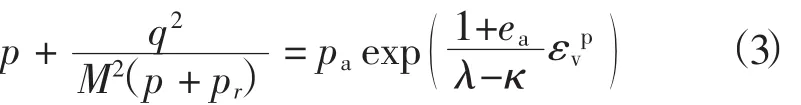
其中：pr=c cot φ

式中：λ为υ-ln p平面中正常固结线的斜率，简称压缩指数；κ为υ-ln p平面中回弹线的斜率，简称回弹指数；pa、ea为初始应力（可取作大气压力）及其孔隙比；c、φ为土的黏聚力、内摩擦角。

1.3 接触面模型

ABAQUS[13]采用有限滑动的库仑摩擦模型来模拟墙与土体之间的摩擦。在库仑摩擦模型中，2个接触面在开始相互滑动之前，在其界面上会产生等效剪应力τeq：

式中：τ1为接触面上1方向的剪切（摩擦）应力；τ2为接触面上2方向的剪切（摩擦）应力。

临界剪应力τcrit与法向接触应力pn成正比，并应小于极限剪应力τmax，表示为：

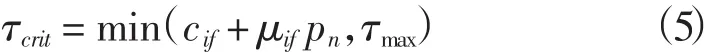
其中：μif=tan φif

式中：μif为摩擦系数；cif、φif为接触面的黏聚力、摩擦角；τmax为极限剪应力，相当于结构与土体的极限侧摩阻力。τeq＞τcrit时接触面之间开始发生相对滑动。

接触的三种状态，可由以下条件判定。

1）黏结状态

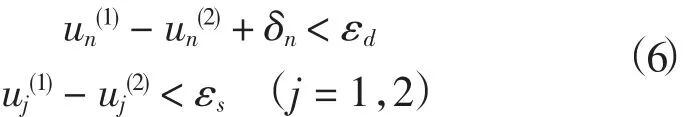
式中：n表示接触面的法向；j=1，2表示接触面的两个相互垂直的切向；δn为接触初间隙；εd为发生分离的临界值；εs为发生滑移的临界值。

2）滑动状态

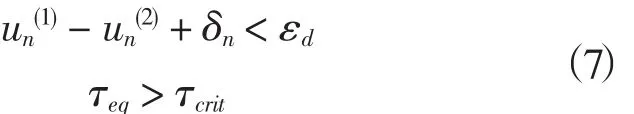
3）分离状态

模拟实际工程中的摩擦行为可能是非常困难的，因此在默认的大多数情况下，ABAQUS采用罚刚度方法[13]，引入了一个“弹性滑动”的罚摩擦公式，允许处于黏结状态的接触面之间可以发生非常微小的“弹性滑移”，ABAQUS会自动选取“罚刚度”的大小。罚摩擦公式对于大部分的接触问题都能很好的解决。

2 回弹再压缩数值模拟

2.1 数值试验模型

为了模拟土体的回弹再压缩过程，设有长×高为54.1 m×31.5 m的二维平面应变地基，基坑深度为9 m，坡度为1∶2，底部半宽20 m，顶部半宽38 m。计算3个分析步：基坑分3次开挖，每层厚度3 m→基坑分3次回填，每层厚度3 m→施加均布荷载171 kPa。模型如图1示意，左右边界设置法向约束，底部设置固定约束。

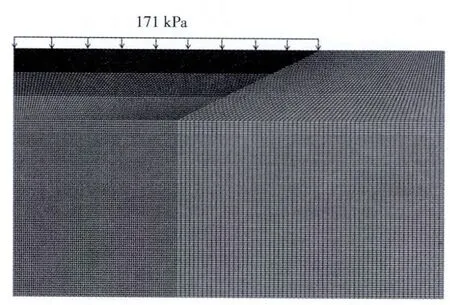
图1 土体回弹再压缩试验模型

2.2 模型的适用性验证

图2显示了基底中心在不同施工步的竖向位移历程。地基土体采用修正剑桥模型，取γ=19.0 kN/m3，e0=0.80，ν=0.35，λ=0.08，κ=0.005，M=1.2。可以看出，在第1步开挖阶段基底卸载19.0×9.0=171 kPa，产生了5.2 cm的隆起量，约为基坑深度的0.58%；在第2步基坑回填完毕后，土体的应力状态恢复到未开挖之前，因此回填产生的再压缩量和开挖产生的回弹量近似相等，这时的基底位移接近为零。在第3步施加的均布荷载171 kPa约等于回填土荷载，此时土体应力状态已处于正常加载曲线上，因此产生的沉降增量40 cm，大于回弹量或再压缩量。从已有的大量的工程经验来看，反映的规律是正确的。

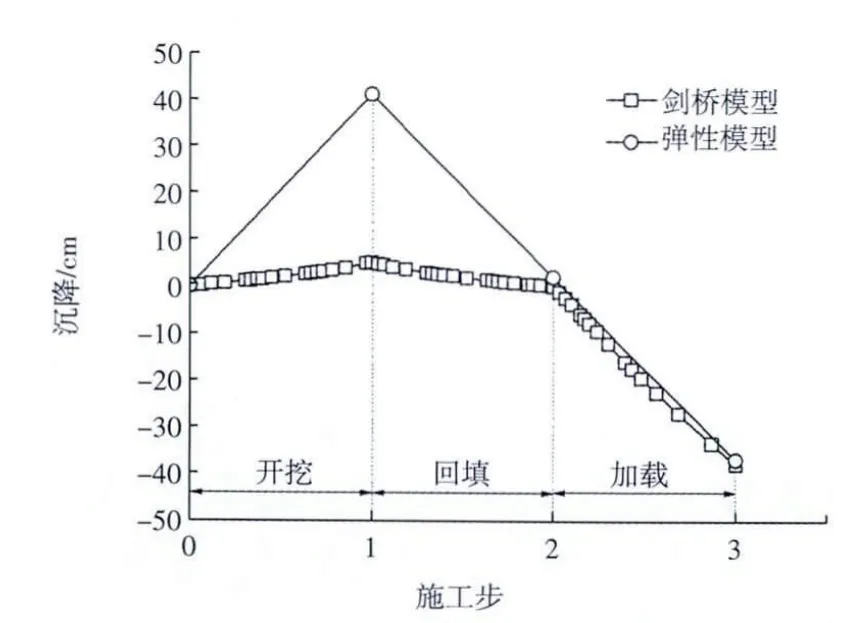
图2 基底中心的沉降

图2还可以看出，由于弹性模型无法反映应力历史及其模量的变化，因此3个阶段计算的竖向位移增量基本相同，计算结果有悖于实际工程情况。

2.3 模型参数的影响

2.3.1 初始孔隙比e的影响

在修正剑桥模型中，回弹体积模量Ks和正常固结体积模量Kc可以表示为[14]：

式（9）表明，e越大，Ks、Kc也越大，3个阶段的土体压缩变形越小。当e从1.2减少到0.6时，各阶段基坑竖向位移增大约37%，如图3所示，可以看出初始孔隙比e对基坑底部竖向位移影响较大。

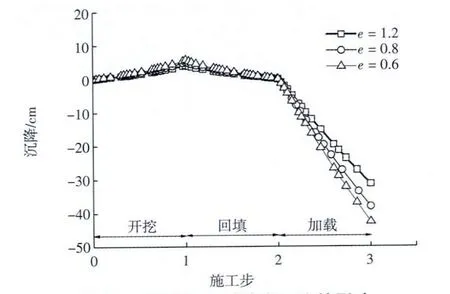
图3 孔隙比e对基底沉降的影响

2.3.2 泊松比ν的影响

土体的抗剪模量G可以表示为[14]：

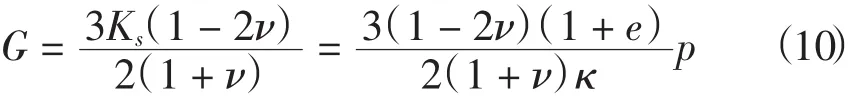
式（10）表明，ν越大，G越小，土体剪切变形越大。当ν从0.25增加到0.45时，两侧边坡土体对基底的挤压作用更加明显，回弹量增大432%，见图4。

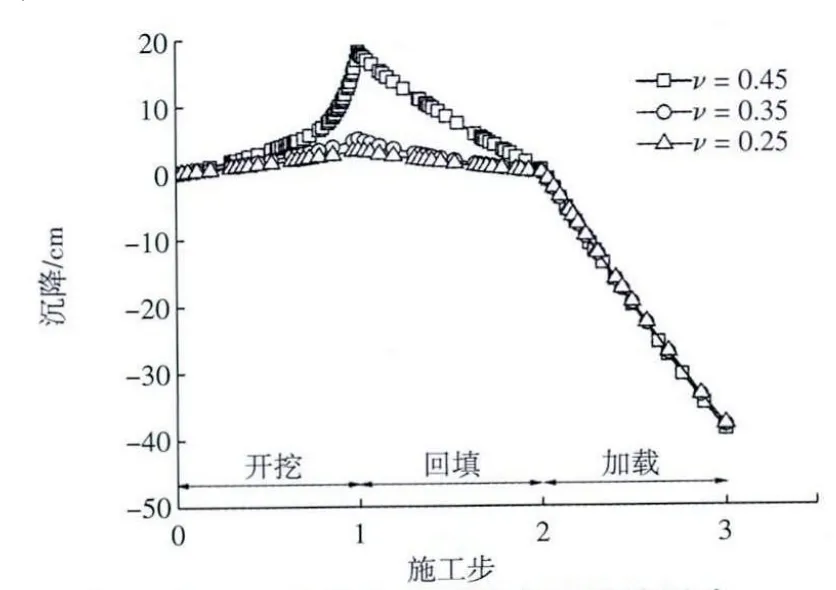
图4 泊松比ν对基底沉降的影响

从图4可以看出，泊松比ν对基坑回弹变形有着重要的影响，而在第3阶段以压缩变形为主，ν的影响不大。

2.3.3 回弹指数κ、压缩指数λ的影响

当κ从0.003增加到0.007时，显著影响回弹量、再压缩量（增大133%），而对第3阶段的坑底变形没有影响。当λ从0.05增加到0.12时，回弹量、再压缩量不变，而在第3阶段的基底沉降增大128%。

3 扶壁式闸墙有限元分析

3.1 计算模型

邵伯三线船闸为Ⅱ级船闸，通行2 000吨级船舶，基本尺度为23 m×260 m×5 m（口门宽×闸室长×槛上水深）。承受双向水头，正向设计水头4.5 m，反向设计水头1.8 m。扶壁式闸墙底宽12.5 m，底板厚0.9 m，立板厚0.6 m，肋板厚0.5 m。闸墙顶高程10.23 m，底板顶高程-1.67 m，前趾长2.4 m，趾底高程-3.87 m，闸墙总高度14.1 m。闸室每个结构段长20.0 m，肋板中心间距4.25 m，取其中一半结构建模，子结构总厚度2.125 m，肋板处厚度0.25 m，具体见图5所示。

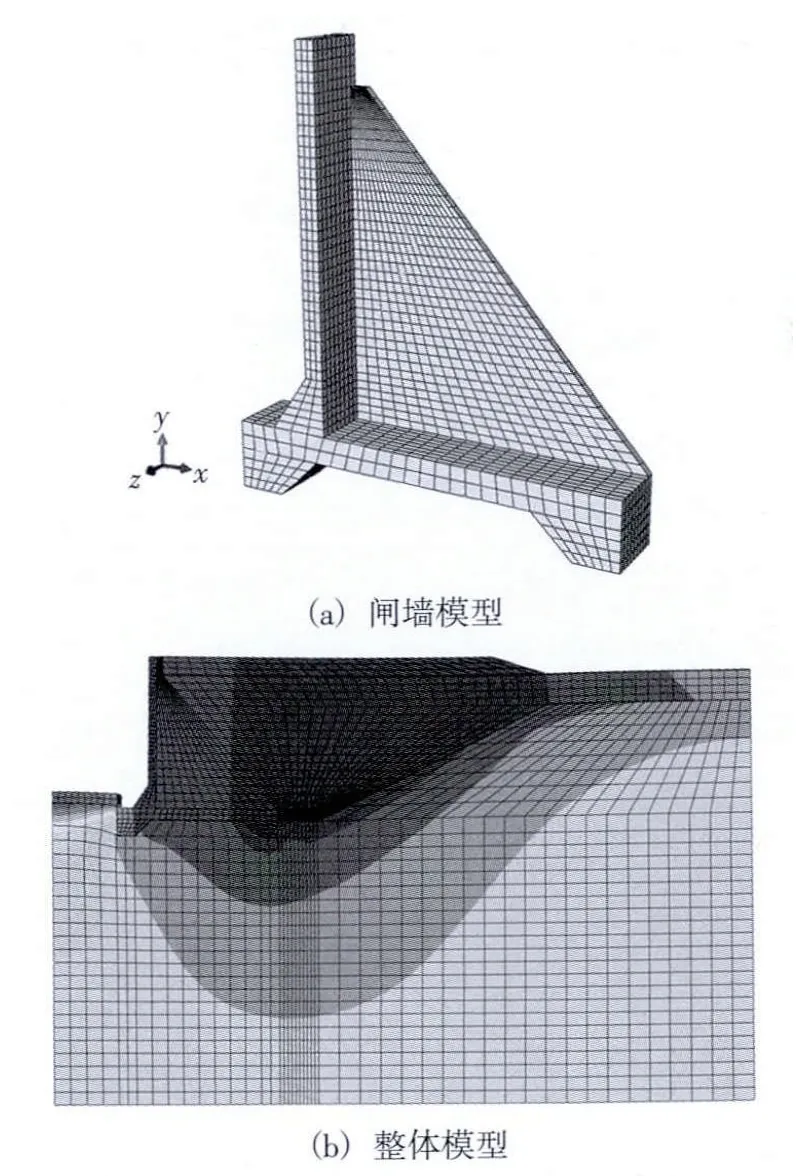
图5 扶壁式闸墙的有限元计算模型

三线闸室的右侧闸墙位于二线船闸施工的抛填土区，地面高程约6.41 m。三线基坑边坡1∶2，开挖的同时将在外侧堆土至高程8.83 m，然后在闸墙回填土时，高程至10.23 m。二线船闸建成于1987年，其施工时抛填土引起的固结已经完成。对三线船闸而言，应考虑自身基坑开挖、坡顶填土、墙后回填等荷载的作用。边载的计算长度一般不应小于底板半宽的1～1.5倍[2，5]，结合三线船闸的实际情况，边载计算长度36.7 m。

闸室处原始土层沿深度方向可概化为：高程1.00～6.41 m为1素填土层；高程-4.30～1.00 m为2-1黏土层；高程-8.30～-4.30 m为2-2粉质黏土层；高程-15.01～-8.30 m为2-3黏土层；高程-25.07～-15.01 m为2-4黏土层。其下为承载力较高的黏土层，局部粉土夹粉砂。计算深度取至2-4层底处。

模型计算范围确定为长×宽×高=54.1 m×2.125 m×35.3 m，底部采用固定约束，四周侧面采用法向约束。

3.2 材料参数

有限元计算时地基土层采用修正剑桥模型（MCC），而回填土则采用 Mohr-Coulomb模型（MC）。MCC模型需4个模型参数，即λ，κ、M、泊松比ν（或剪切模量G）。MC模型有4个参数，即黏聚力c，内摩擦角φ，泊松比ν和弹性模量E。

其中λ、κ可根据固结试验由式（11）求得[15]。

式中：Cc、Cs分别为土在e-ln p平面的压缩指数、回弹指数。许多学者对λ和κ之间的关系进行了统计，λ/κ一般介于5～10，本文分析时取λ/κ=10，即根据λ来确定κ。

M可根据三轴压缩试验由式（12）得到[15]：

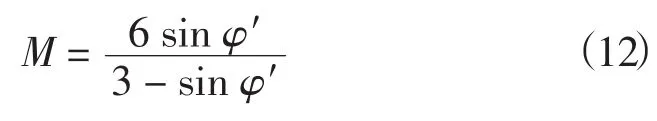
式中：φ′为三轴试验得到的有效内摩擦角。

根据地质勘查资料，计算的材料参数可见表1。

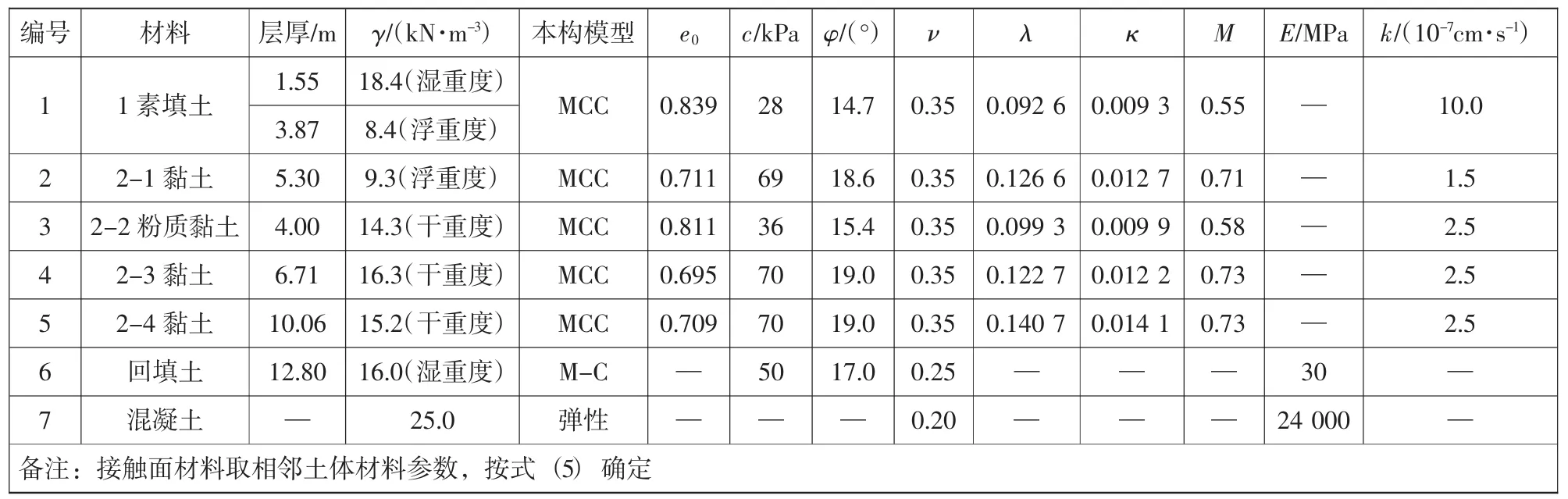
表1 材料参数

3.3 计算结果分析

在修正剑桥与渗流固结耦合模式下，扶壁式闸室墙计算主要模拟了以下几种工况：基坑一次开挖（2个月）→渗流固结计算10个月→浇筑闸墙（10个月）→浇筑闸底格梗（1个月）→回填土填筑（6个月）→固结计算7个月。竖向位移-时间曲线以基坑开始开挖时为时间零点，共3 a。回填土完成前，地下水位在基底高程-3.87 m以下，填筑完成后，地下水位上升至高程4.5 m。

从图6的地基沉降-时间曲线来看，基坑开挖使得基底产生了50.8～52.4 mm的隆起，而且在闸墙浇筑前回弹尚未完成。闸墙浇筑后，由于结构重心偏向前趾，此时前趾的沉降增量大于后趾沉降增量。在闸底格梗浇筑时，由于底板引起的边载作用，前趾产生沉降增量，而后趾略有上翘增量。

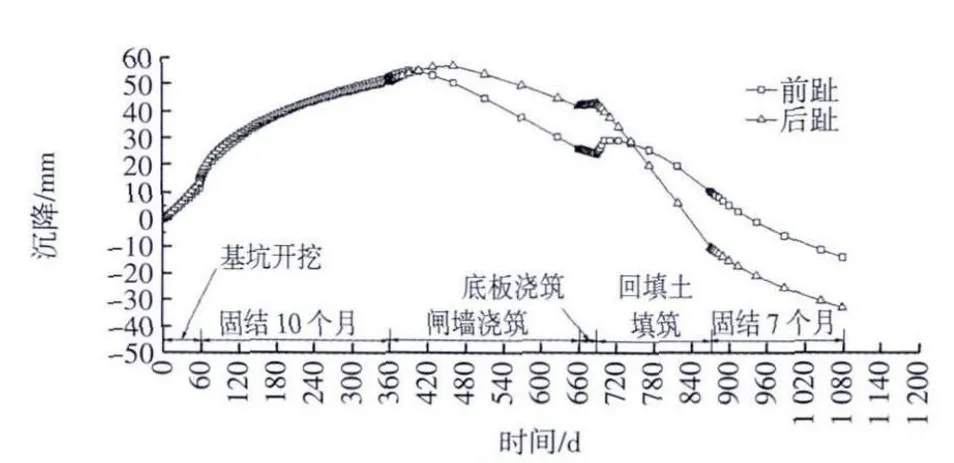
图6 地基沉降-时间曲线

在回填土填筑阶段，由于墙后填土的边载作用，后趾的沉降速率明显加大，经过一段时间后大于前趾的沉降量。完建后7个月时，前趾、后趾产生的沉降量分别为66.5（52.4+14.1）mm、83.6（50.8+32.8）mm，沉降量差为17.2 mm。考虑到闸墙底宽为12.50 m，倾斜度i1=17.2 mm/12.50 m=0.14%。经预测前趾、后趾最终沉降量分别为104.2 mm、121.5 mm。

从图7中可以看出，墙底水平位移始终极小。闸墙、格梗浇筑完成时，墙顶向前位移16.8 mm、20.0 mm，整体呈前倾趋势。在墙后填土完成时，墙顶向后位移21.7 mm。完建后7个月，墙顶向后位移值为19.4 mm，后倾量减小。闸墙高度为10.23-（-1.67）=11.90 m，倾斜度为i2=19.4 mm/11.90 m=0.16%。

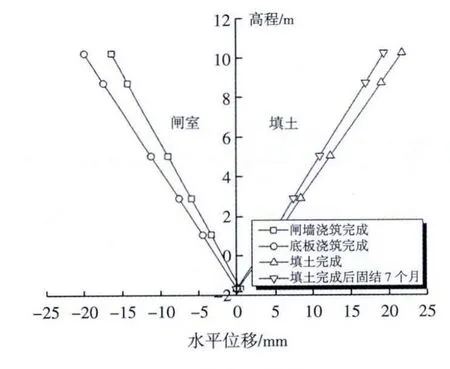
图7 闸墙水平位移

4 结语

1）采用修正剑桥与渗流固结耦合模型，可以更好地模拟地基土固结特性、回弹再压缩特性，合理反映基坑暴露时间、地基土渗透系数、回弹模量、泊松比、应力路径、应力水平等因素对再压缩的影响。邵伯三线闸墙由于地基再压缩引起的沉降占41.8%～50.2%，因此进行考虑基坑卸荷再加荷影响的有限元分析是必要的。

2）扶壁式闸墙的水平位移主要由三部分组成：水平力作用下闸墙整体水平位移及墙身挠曲变形、不均匀沉降导致闸墙倾斜。由于闸墙前趾受到格梗的约束作用、墙身刚度较大，前两项位移可以忽略不计。

3）闸室墙、闸底格梗浇筑完成后，闸室墙前倾；随着回填土填筑，闸室墙逐渐向后倾斜；完建后地下水位上升使得后倾有所减小，计算分析的倾斜规律与实测情况一致。交工时，闸墙平均沉降75.1 mm，后倾率为0.15%。因此，建议闸墙预留沉降50 mm，预留前倾量0.08%为宜。

[1]DUNCAN J M，CLOUGH G W.Finite Element Analysis of Port Allen Lock[J].ASCE，Journal of the Soil Mechanics and Foundations Division，1971，97（8）：1 053-1 068.

[2]刘晓平，陶桂兰.渠化工程[M].北京：人民交通出版社，2009：136-139.

[3]张子明，赵光恒.有限深弹性层地基表面在矩形均布荷载作用下的沉陷计算[J].华东水利学院学报，1986，14（1）：67-78.

[4]何良德，梅霆，周俊波，等.基于分层地基模型的闸首分缝底板计算方法[J].河海大学学报：自然科学版，2012，40（6）：698-703.

[5]JTJ 307—2001，船闸水工建筑物设计规范[S].

[6]陈璐，刘永强.自重折扣法在坞式底板设计中的应用探讨[J].水利水电科技进展，1999，19（6）：41-43.

[7]周清华，边立明，徐泽中.墩底分浇式船闸闸首底板算法研究[J].水运工程，2003（1）：13-16.

[8]冯大江.应用Biot固结理论的船闸闸首结构非线性有限元分析[D].南京：河海大学，2005.

[9]ROSCOE K H，SCHOFIELD M A，THURAIRAJAH A.Yield of Clays in States Wetter than Critical[J].Geotechinique，1963，13（3）：211-240.

[10]BURLAND J B.The Yielding and Dilation of Clay[J].Geote chinique，1965，15（2）：211-214.

[11]JTS 257—2008，水运工程质量检验标准[S].

[12]殷宗泽.土工原理[M].北京：中国水利水电出版社，2007：350-364.

[13]庄茁，张帆，岑松，等.ABAQUS非线性有限元分析与实例[M].北京：科学出版社，2005：312-385.