一类污染物扩散问题全离散间断有限元方法的误差分析

杨继明，安翠昭

（湖南工程学院 理学院，湘潭411104）

考虑环境问题中一类较集中的污染物质在多孔介质中扩散的数学模型：

其中Ω是R2上的有界多角区域，z是污染物质的浓度，f∈L2（0，T；L2（Ω）），gD∈L2（0，T；H1／2（∂Ω）），z0∈L2（Ω），α∈L∞（Ω），α＞0.假设K 一致有界，即对∀x∈Ω，有0＜K0≤K（x）≤K1.

间断有限元方法是一类非协调元，有着很好的物理和数值特性，在数值计算中被广泛应用［1－6］.在文献［5－6］中，作者给出了全离散间断有限元方法的后验误差估计.

为了求解问题（1），我们采用全离散间断有限元方法并给出先验误差分析.

1 全离散间断有限元方法

设εh为Ω的拟一致网格剖分，Γh为所有内边的集合.对于网格剖分中的单元E，其网格尺寸为h.

引入间断Sobolev空间：

设Ei和Ej为两相邻单元，它们的公共边为e，在e上外法向指向Ei.定义函数v在e上的平均和跳跃为：

定义间断有限元空间为

Dk（εh）＝｛v∈L2（Ω）∶v｜E∈Pk（E），E∈εh｝，其中Pk（E）表示在E上自由度小于等于k的多项式函数空间.

首先，引入双线性形式和线性泛函：

其中σ＞0为罚参数，｜e｜为e的面积，β＞0.

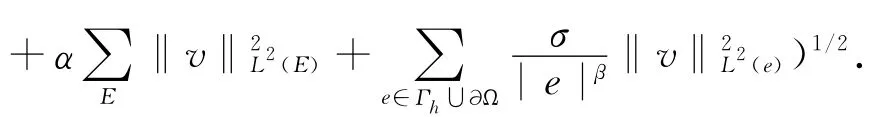
根据双线性形式a的定义，利用迹不等式和逆不等式可以得到双线性形式a的强制性和连续性.

引理1（强制性）存在一个与h无关的正常数Cd使得对∀v∈Dk（εh）有a（v，v）≥Cd‖v‖2ε成立.

引理2（连续性）存在一个与h无关的正常数Cb使得对 ∀v，w ∈Dk（εh）有

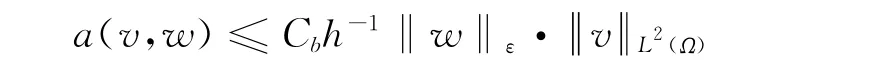
成立.

然后，我们给出问题（1）的弱形式.设v∈Hs（εh），s＞3／2，对于所有t＞0，有

令N为正整数，Δt＝T／N 表示时间步长.对∀n≥0，tn＝nΔt.对任意的函数u（x，t），我们记un（x）＝u（x，tn）.采用向前欧拉方法对时间进行离散，便得到全离散间断有限元格式：寻找∈Dk（εh），使得

2 误差估计

我们给出用全离散间断有限元方法（3）求解问题（1）的先验误差估计.

定理1 假设问题（1）的解满足：

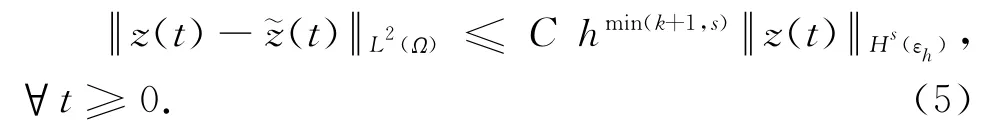
记zn－＝ρn－χn，其中－～zn.

从（2）式中减去（3）式，并取v＝χn＋1得到：

于是，

由引理1推出a（χn＋1，χn＋1）≥Cdχn＋1.由引理2和Young不等式，可知利用Cauchy－Schwarz不等式、Poincare不等式和Young不等式，得

用Cauchy－Schwarz不等式，可以推知

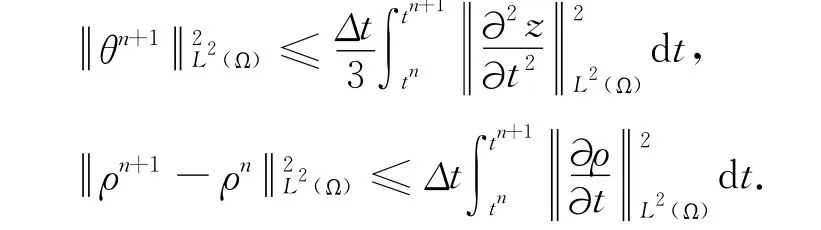
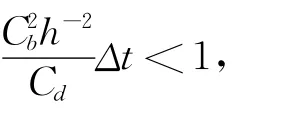
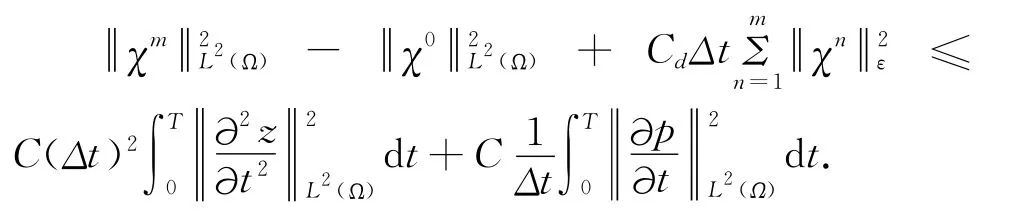
由χ0＝0和投影估计（5），得

再利用三角不等式，我们便可得到（4）式.证毕.

［1］ D Arnold，F Brezzi，B Cockburn and D Marini.Unified Analysis of Discontinuous Galerkin Methods for Elliptic Problems［J］.SIAM J.Numer.Anal.，2002，（3915）：1749－1779.

［2］ B Riviere.Discontinuous Galerkin Methods for Solving Elliptic and Parabolic Equations：Theory and Implementation（Frontiers in Applied Mathematics）［M］.SIAM.Philadelphia，PA，USA，2008.

［3］ B Riviere，M F Wheeler，and V Girault，A Priori Error Estimates for Finite Elementmethods based on Discontinuous Approximation Spaces for Elliptic Problems［J］.SIAM J.Numer.Anal.，2001，39：902－931.

［4］ S Sun and M F Wheeler.Symmetric and Non－symmetric Discontinuous Galerkin Methods for Reactive Transport Problem in porous media［J］.SIAM J.Numer.Anal.，2005，43（1）：195－219.

［5］ J Yang and Y Chen.A Posteriori Error Analysis for a Fully Discrete Discontinuous Galerkin Approximation to a Kind of Reactive Transport Problems［J］.J.Syst.Sci.Complex.，2012，25（2）：398－409.

［6］ Y Chen and J Yang.A Posteriori Error Estimation for a Fully Discrete Discontinuous Galerkin Approximation to a kind of Singularly Perturbed Problems［J］.Finite Elem.Anal.Des.，2007，43（10）：757－770.