离散型随机变量数字特征的计算方法
2013-08-11赵天玉长江大学信息与数学学院湖北荆州434023
赵天玉,李 茜 (长江大学信息与数学学院,湖北 荆州434023)
随机变量的数字特征描述了随机变量变化的全貌特点:数学期望或均值描述了随机变量取值的集中位置或平均大小,方差描述了随机变量的取值偏离均值的程度或分散程度。因此,研究随机变量数字特征的计算方法非常必要。在一般的教学过程中,仅仅只介绍随机变量均值和方差的计算公式,给出它们的性质,列举几个例子就完成了任务[1],很少对均值和方差的计算方法进行系统的概括总结,几乎没有对这些内容进行延伸与扩充,导致学生只会套用公式计算期望与方差,遇到稍微复杂一点的问题就束手无策。为此,笔者以离散型随机变量为研究对象,以母函数为研究工具,讨论了离散型随机变量数学期望和方差的3种计算方法❶❶长江大学精品课程 《概率论与数理统计》。。
1 公式法
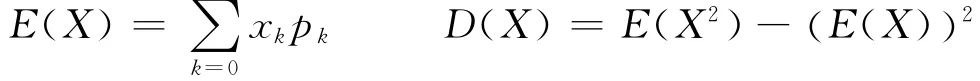
这就是离散型随机变量X的期望与方差的计算公式。
如,若X~b(1,p),则:
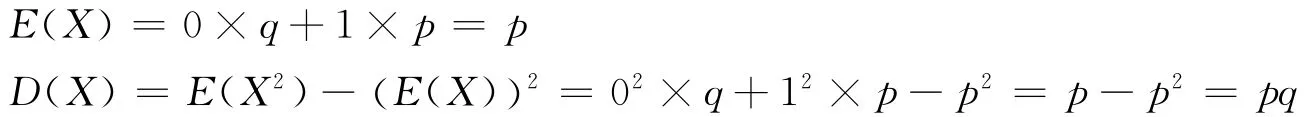
若X~Ge(p),则:
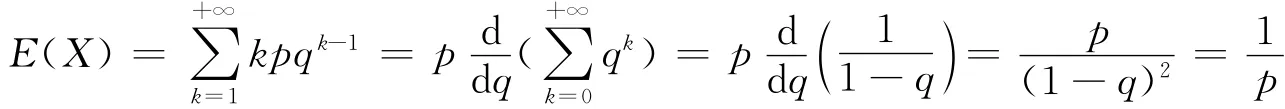
又因为:
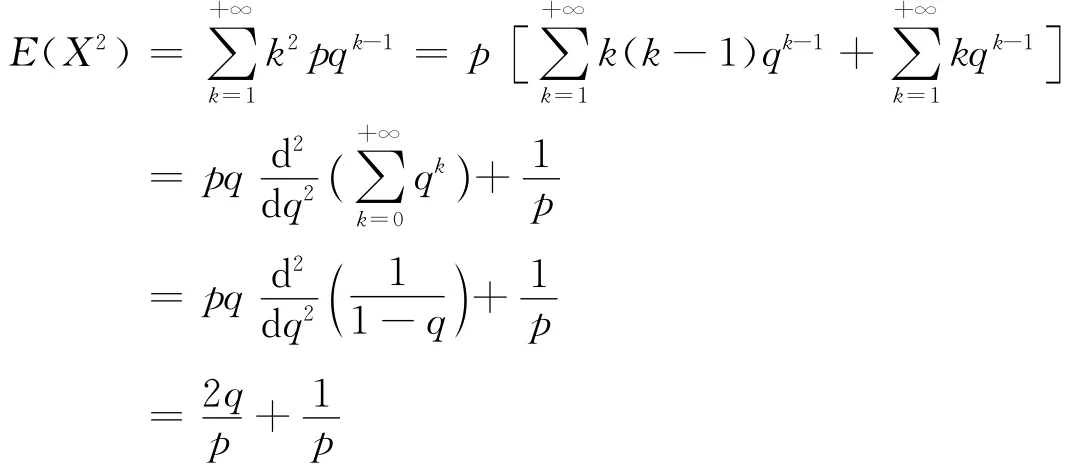
由此得X的方差为:
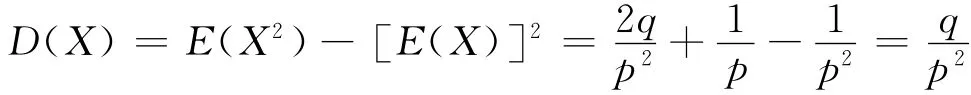
若X~π(λ),则:
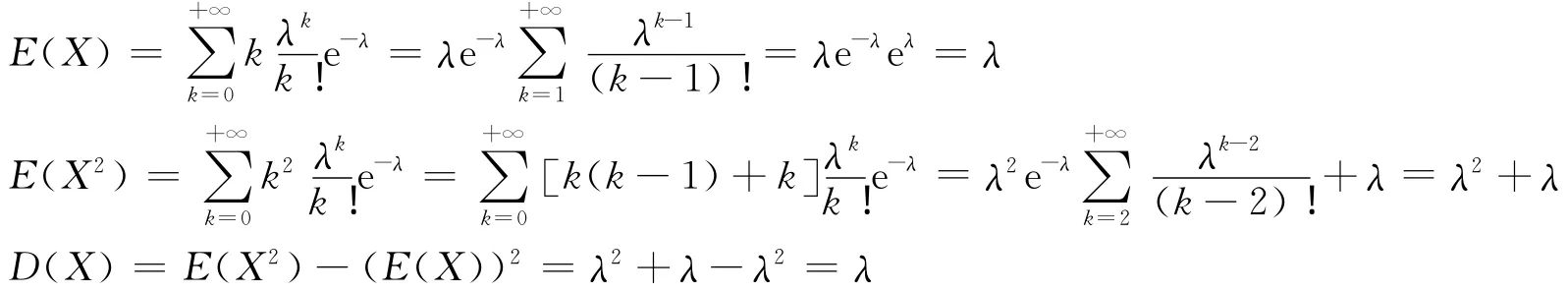
2 随机变量分解法
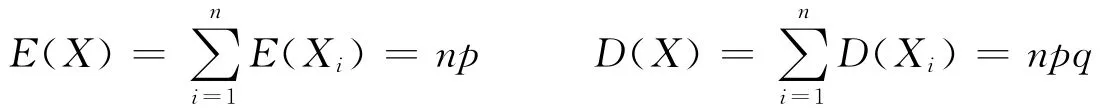
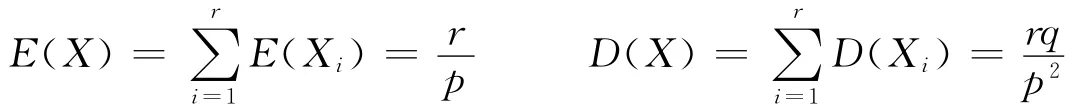
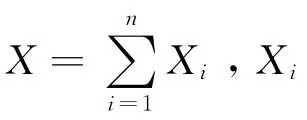
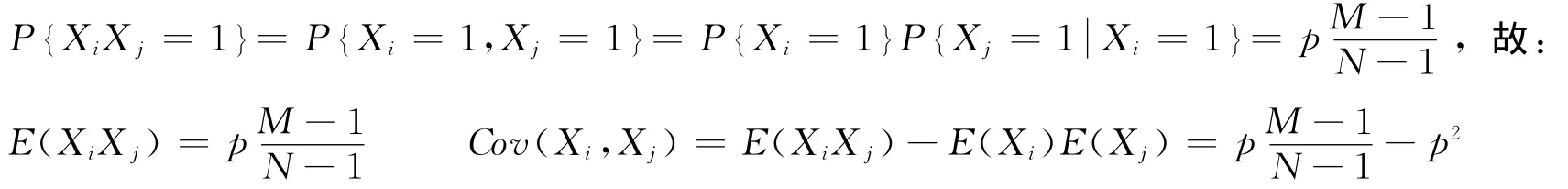
最后由期望与方差的性质得:
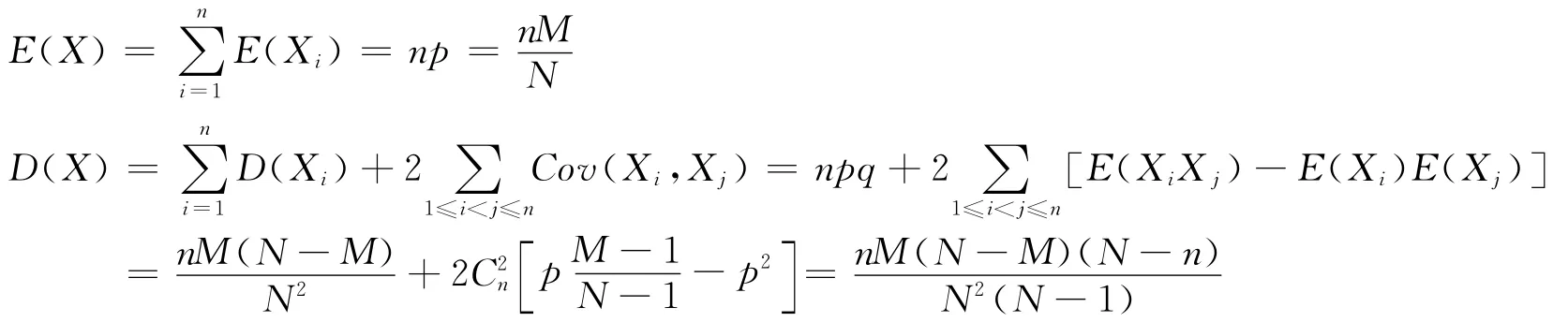
3 母函数方法
母函数有如下性质[4,5]:
(1)概率分布与母函数是一一对应的。对于概率分布的许多研究可化为对其所对应的母函数的研究。
(2)若随机变量X1,X2,…,Xn相互独立,它们的母函数分别为G1(s),G2(s),…,Gn(s),则X=X1+X2+,…,+Xn的母函数为G(s)=G1(s)G2(s),…,Gn(s)。
特别地,当X1,X2,…,Xn独立同分布时,Gi(s)=G1(s),这时G(s)= [G1(s)]n。
(3)设X1,X2,…,Xn,,…,是一串独立同分布的取非负整数值的随机变量,其母函数为g(s),随机变量Y是取正整数值的,其母函数为G(s)。若 {Xn}与Y独立,则Z=X1+X2+,…,+XY(若Y=0,则定义Z=0)的母函数为H(s)=G [g(s)]。
(4)当X 的期望与方差存在时,E(X)=G′(1),D(X)=G″(1)+G′(1)- [G′(1)]2。
下面给出用母函数计算数学期望及方差的简便公式:
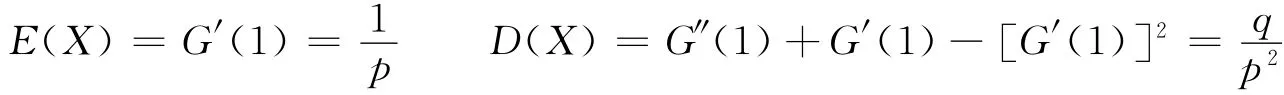
(2)若X ~π(λ),G(s)=eλ(s-1),则:E(X)=G′(1)=λ D(X)=G″(1)+G′(1)- [G′(1)]2=λ
(3)若X ~b(n,p),G(s)= (q+ps)n,则:E(X)=G′(1)=np D(X)=G″(1)+G′(1)- [G′(1)]2=npq
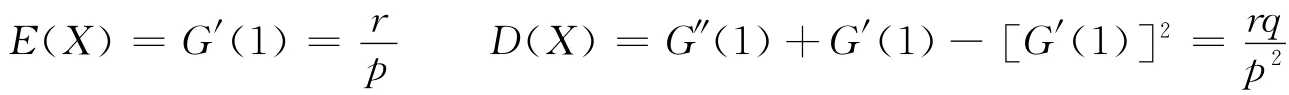
(5)设 Z 是 母 函 数 的 性质 (3)中的 随 机 变 量,此 时 H(s)= G [g(s)]。由于 H′(s)=G′[g(s)]g′(s),H″(s)=G″[g(s)][g′(s)]2+g″(s)G′[g(s)],因此当E(Xi),E(Y),D(Xi),D(Y)存在时,有:
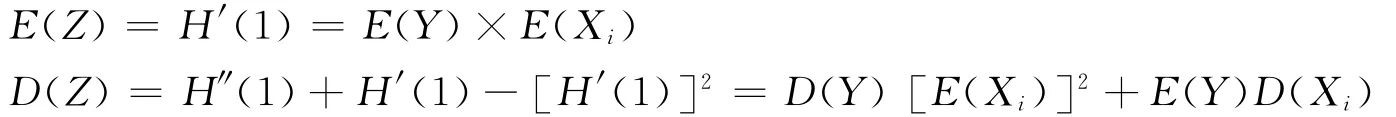
这是计算随机个独立同分布的随机变量之和的期望与方差的公式。
(6)设X1,X2,…,Xn,…,是独立同分布于0-1分布的随机变量序列,Y~π(λ),且与X{}n相互独立,则Z=X1+X2+…+XY的期望与方差分别为:
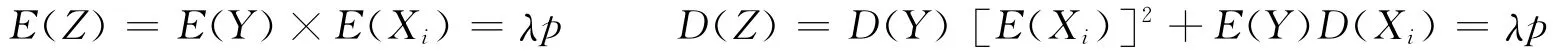
这个结果可从母函数 H(s)=G [g(s)]=eλ(q+ps-1)=eλp(s-1)得到验证,因为Z ~π(λp)。
(7)设X1,X2,…,Xn,…,是独立同分布于参数为p1的几何分布的随机变量序列,Y~Ge(p2),且与 {Xn}相互独立,则Z=X1+X2+…+XY的期望与方差分别为:
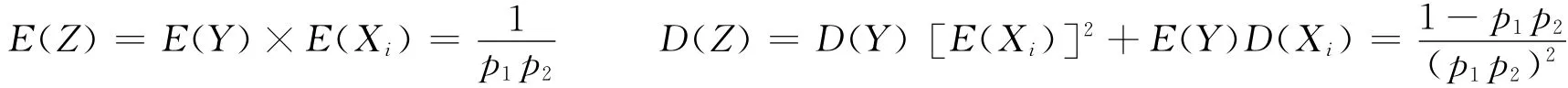
[1]李正耀,周德强 .概率论与数理统计 [M].北京:科学出版社,2009:80-97.
[2]侯文 .常用概率分布间的关系 [J].辽宁师范大学学报,2005,28(4):503-505.
[3]匡能晖 .超几何分布的数学期望和方差的定义求法 [J].高等数学研究,2010,13(4):73-74.
[4]复旦大学 .概率论 (第一册:概率论基础)[M].北京:人民教育出版社,1979.
[5]赵天玉 .基于母函数的常用离散型随机变量概率分布研究 [J].长江大学学报 (自然科学版),2013,10(28):1-3.
