基于无限元法研究阻尼对船舶结构水下声辐射特性影响
2013-08-11邱中辉
邱中辉 吕 帅 郑 律 丛 刚
(哈尔滨工程大学船舶工程学院 哈尔滨150001)
0 引 言
船舶水下声辐射问题即在无界区域上求解声波方程的问题[1]。原有的有限元法通过在边界上设置无反射或声阻抗条件来模拟无限域,但要保证计算精度,所建立的有界流场区域,一般为结构尺度的4~6 倍,模型规模大,计算效率不高[2]。
声学无限单元是向外法向发散的“特殊“有限元,通过引进边界,将无界区域分离成有界的计算区域和外部的无界区域。在边界外引入一种无限大的“有限”单元模拟无限大流场[3]。每个单元只有4个节点,且无截断误差,只有离散误差,其数值计算精度和效率都高于有限元法[4]。
1 声学无限元法
均匀球面波在声学介质传播过程中,辐射空间中的声压等声学量随时间和空间的变化可由声波方程(1)表示:
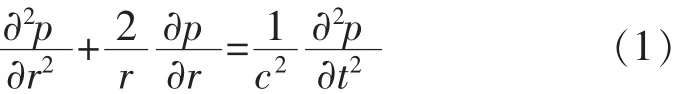
以图1活塞振动为例,假设在r=a处有一活塞,其表面作一致谐响应振动,振速幅值大小为U,此时施加速度边界条件为:
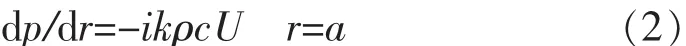
式中:p为辐射声压;r为半径;c为声速;t为时间;k=ω/c为波数。
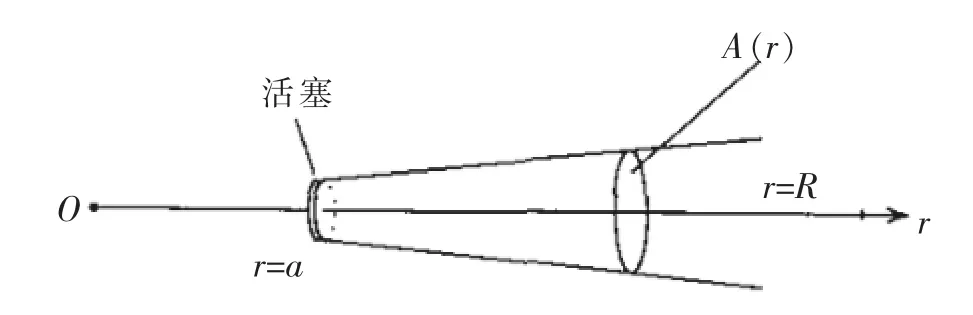
图1 活塞振动示意图
在无穷远处需满足Sommerfied辐射边界条件:
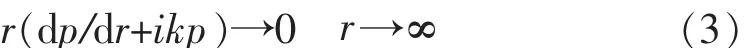
得解析解为:
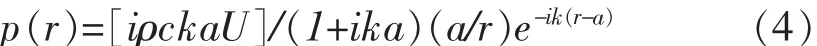
假定声压p(r)的试函数形式表示为:
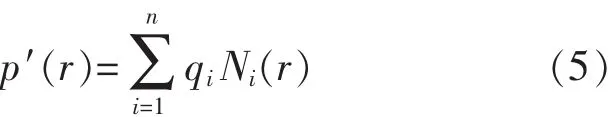
式中:Ni(r)为基函数;
qi为待求系数。
为便于理论推导,设边界条件(3)施加在有限长边界r=R处,再令R趋向无穷大,便可将有界域问题转化并得出无界域结果。此时边界条件(3)可表示为:
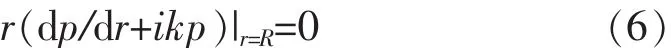
设权函数取为 wi(r)(i=1,2,…n),利用加权残值法及边界条件可以得到:
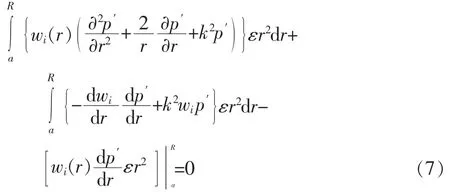
整理得:
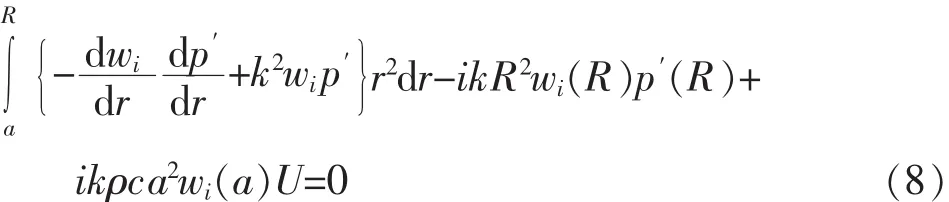
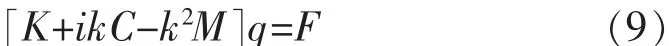
其中:
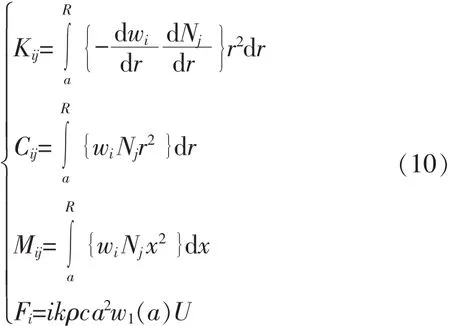
以一维无限单元为例,节点C、P、Q是构成无限单元的几何要素(如图2),节点R延伸到无穷远处模拟无界边界,映射函数表达式直接写出基于节点P、Q 的坐标,可以写成[5]:
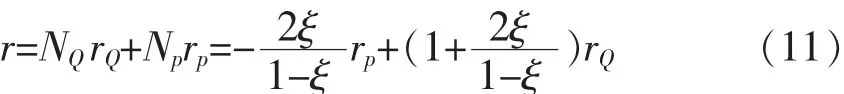
式中:ξ为r对应的映射坐标。

图2 一维无限单元
通过映射函数变换,无限域声学问题转换为有限域声学问题,选取合适的形函数及权函数,可以得到模型的刚度矩阵、阻尼矩阵、质量矩阵、载荷矩阵。权函数及附加系数对收敛速度有影响。
2 远场声辐射特性
2.1 圆柱艇体
用锥柱混合结构简化模拟潜艇结构,如图3所示。

图3 圆柱艇体结构
在艇体艉部推进主机部位,施加一个向激励载荷、模拟主机引起的不平衡激扰力[6]。将壳体外表面作为人工边界,截断无限大流场。在人工边界外引入一种几何上无限大的“有限”单元,模拟无限大声学流场单元,且与结构有限元单元直接耦合。将壳体结构几何中心处设置一个参考点C,作为虚拟生源且视作声辐射的起点。
振动传递到壳体外表面的单元节点P上,如图2所示,沿CP方向映射到无限域的声场单元Q上。进而不需要外流场,利用无限单元可以得到远场辐射声压。以下为距参考点虚拟声源100 m处频率为20 Hz、100 Hz、 200 Hz、300 Hz,结构阻尼分别为noloss、0.001、0.01、0.025 的流场声压云图如图 4。

图4 圆柱艇体结构流场声压云图
2.2 双柱艇体
用锥柱混合结构简化模拟潜艇结构,模型中部采用单双壳两种结构作为对比,如图5所示。

图5 双柱艇体结构
保持其他结构与载荷情况一致。同样提取距参考点虚拟声源100 m处频率为20 Hz、100 Hz、200 Hz、300 Hz, 结构阻尼分别为 noloss、0.001、0.01、0.025的流场声压云图如下页图6所示。
由图4与图6可见,对于潜艇等细长体结构,沿艇长方向振动能量主要传递到艏位部,辐射声压较大,指向性较强。由于载荷激励在靠近艉部推进电机处,且艉部壳体为锥型,映射网格较密,远场声压值较大。
频率越高,红色区域(即声压较大的区域)越集中在艉部。这是因为,频率越高、振动波波长越小、结构阻抗对其影响越大、振动波能量被反射得越多、因此引起局部振动的频率越高,辐射声压越集中在艉部。在同一频率下,阻尼越大、振动波向前传播更困难,声压较大区域约集中在艉部。
3 阻尼对声辐射特性影响
为了数学计算的方便,将阻尼描述为结构振动过程中能量耗散的机理。影响阻尼的因素很多,主要有介质阻尼、结构阻尼、材料内阻尼、辐射阻尼等[7]。

图6 双柱艇体结构流场声压云图
3.1 材料阻尼对声辐射特性影响
以下将船体结构材料属性中的结构损耗因子设置分别为 noloss、0.001、0.025、0.01,通过频域内谐响应计算在20~300 Hz的低频段频率范围内,艇体水下声辐射特性,得到艇体水下远场辐射声压。图7、图8为距虚拟声源100 m处辐射声压随频率的变化曲线。
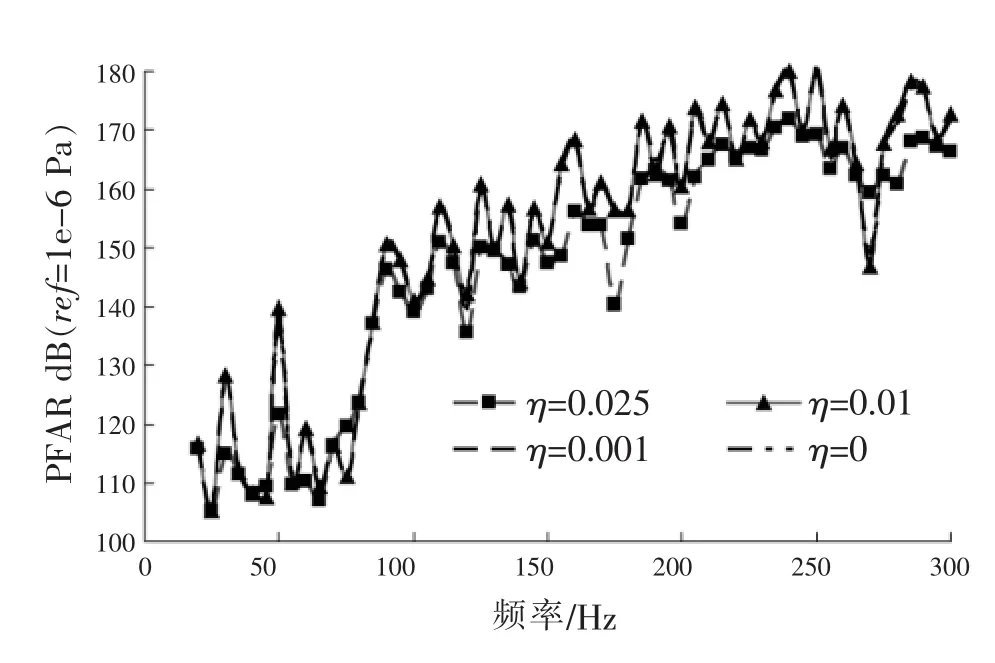
图7 圆柱结构辐射声压随频率变化曲线
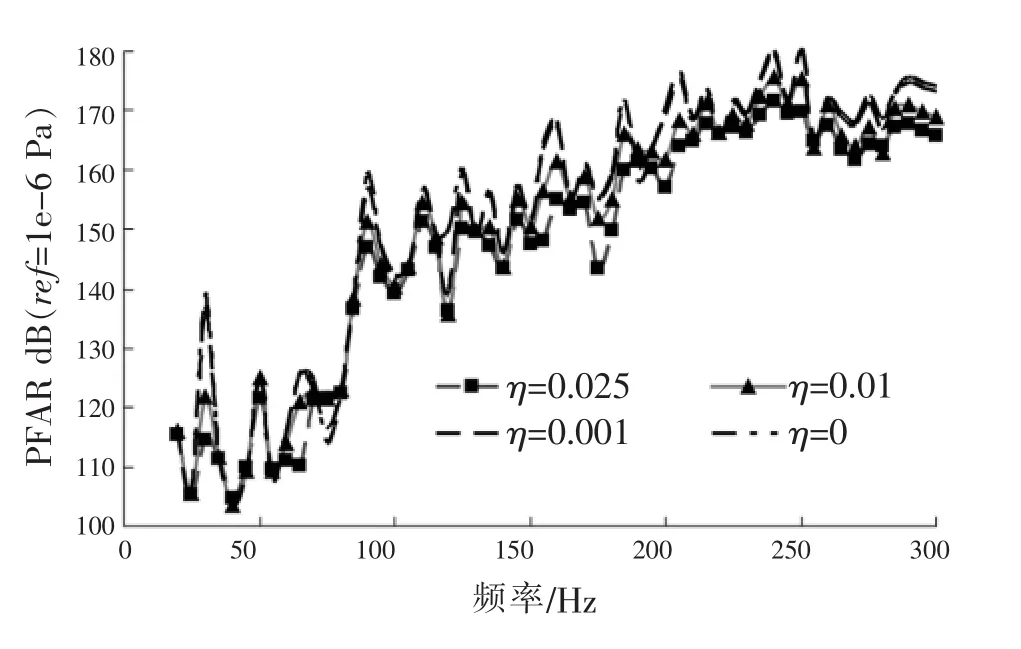
图8 双柱结构辐射声压随频率变化曲线
由图7、图8可见,将艇体材料的结构损耗因子设置得越大,流场中辐射声压越小,说明结构振动能量耗散越大。阻尼为0.025时,辐射声压减小较明显,而结构阻尼为0.01、0.001或无阻尼时的流场辐射声压差别则不明显。材料阻尼在频率较低时,对辐射声压影响很大;频率为200 Hz以上时,材料阻尼对辐射声压影响较小。
3.2 结构阻尼对声辐射特性影响
通过改变圆柱壳结构,在艇体中部将圆柱壳半径加大,采用双圆柱壳结构。由此引起结构的改变,使结构阻抗特性增加。以材料结构损耗因子设置成0.025 阻尼为例, 取频点为 25 Hz、100 Hz、200 Hz、300 Hz时,比较圆柱、双柱两种结构的艉部节点的声辐射特性,曲线如图9所示。
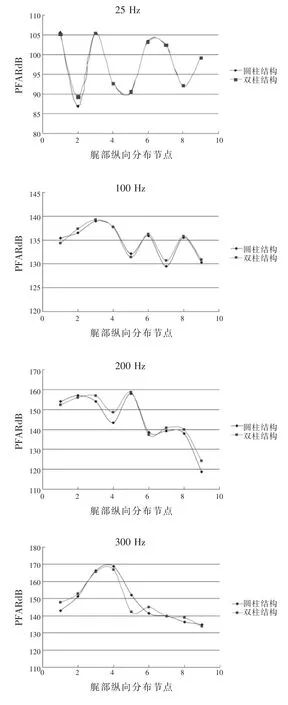
图9 圆柱、双柱结构艉部节点声辐射特性比较
由图9可见,双柱结构比圆柱结构在艇体艉部节点声辐射值更大。这是由于激扰力位置靠近壳体艉部,在保证材料结构损耗因子同为0.025的条件下,双柱结构由于中部结构突起,阻抗增大。当振动波传播时,遇到阻碍作用较大,传到艏部的能量较小,反射回艉部的振动能量较大,因此艉部节点处水中远场声辐射值比单圆柱结构大。
4 结 论
通过声学阻抗原理及声学无限元方法,研究阻尼对船体结构水下声辐射特性的影响,得到以下结论:
(1)利用无限元法求解水下远场辐射声压是可行的,比有限元法计算效率高。
(2)材料结构损耗因子设置得越大,流场中辐射声压越小。阻尼为0.025时,辐射声压减小较明显;而结构阻尼为0.01、0.001以及无阻尼时,流场辐射声压差别不明显。
(3)材料阻尼在频率较低时,对辐射声压影响很大,在200 Hz以上材料阻尼对辐射声压影响较小。
(4)双柱结构由于中部结构突起,阻抗增大,反射回艉部的振动能量较大,因此艉部节点处水中远场声辐射值比单圆柱结构大。
[1]杨瑞梁,汪鸿振.声无限元进展[J].机械工程学报,2003,39(11),82-87.
[2]杨瑞梁,范晓伟.使用有限元和无限元耦合求解声辐射问题[J].振动工程学报,2004,17:1007-1009.
[3]李录贤,国松直,王爱琴.无限元方法及其应用[J].力学进展,2007,37:161-173.
[4]DEMKOWICZ L,GERDES K.Convergence of the infinite element methods for the Helmholtz equation[J].Math,1998,79(1),11-42.
[5]GERDES K.A summary of infinite element formulations for exterior Helmholtz problems[J].Comput Methods Appl.Mech.Engrg.,1998,16(4): 95-105.
[6]谢官模.环肋圆柱壳在流场中的动力响应和声辐射[D].武汉:华中理工大学,1994.
[7]梁超锋,欧进萍.结构阻尼与材料阻尼的关系[J].地震工程与工程振动,2006,26(1):49-55.
