Existence and Uniqueness of Weak Solutions to the p-biharmonic Parabolic Equation
2013-08-10GUOJINYONG
GUO JIN-YONG
(Department of Mathematics and Computer Science,Liuzhou Teachers College, Liuzhou,Guangxi,545004)
Communicated by Gao Wen-jie
Existence and Uniqueness of Weak Solutions to the p-biharmonic Parabolic Equation
GUO JIN-YONG
(Department of Mathematics and Computer Science,Liuzhou Teachers College, Liuzhou,Guangxi,545004)
Communicated by Gao Wen-jie
We consider an initial-boundary value problem for ap-biharmonic parabolic equation.Under some assumptions on the initial value,we construct approximate solutions by the discrete-time method.By means of uniform estimates on solutions of the time-dif f erence equations,we establish the existence of weak solutions,and also discuss the uniqueness.
p-biharmonic,parabolic equation,weak solution,existence,uniqueness
1 Introduction
Suppose that Ω⊂RNis a bounded domain with smooth boundary.Let λ,p and q be positive numbers with p>2 and q>2.In this paper,we consider the following p-biharmonic parabolic initial-boundary value problem:
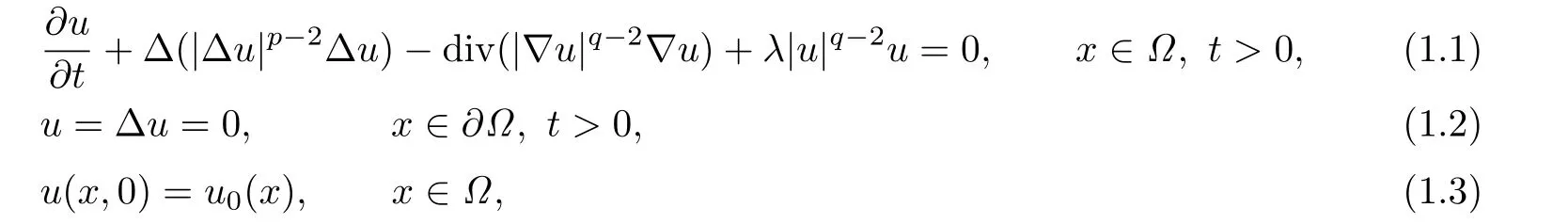
where Δ(|Δu|p-2Δu)is called a p-biharmonic operator.
When p=2 and λ=0,(1.1)becomes
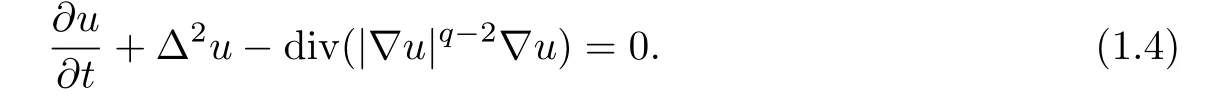
It arises in epitaxial growth of nanoscale thin f i lm(see[1–3]),where u(x,t)denotes the height from the surface of the f i lm in epitaxial growth,Δ2u denotes the capillarity-driven surface dif f usion,and div(|∇u|q-2∇u)denotes the upward hopping of atoms.
Liu and Du[4]studied(1.4)relying on some necessary uniform estimates of the approximate solutions,and they proved the existence of radial symmetric solutions to(1.4)in the two-dimensional space.
When p=q=2 and λ=0,(1.1)becomes a particular case of the following equation in 1-dimension:

with γ=µ=0.It follows from a small-slope approximation to metal surface evolution,with surface-dif f usion and evaporation-condensation represented by fourth-order and second-order dif f usion terms,respectively(see[5–6]).(1.5)with γ=0 can be considered as a semilinear limit of the classical Cahn-Hilliard model of phase separation,which is also widely studied (see[7–9]and the references therein).
(1.1)is a typical higher order equation.Because of the degeneracy,the problem(1.1)–(1.3)does not admit classical solutions in general.So,we introduce weak solutions in the sense of the following def i nition:
Def i nition 1.1A function u is said to be a weak solution of the problem(1.1)–(1.3)if the following conditions are satisf i ed:
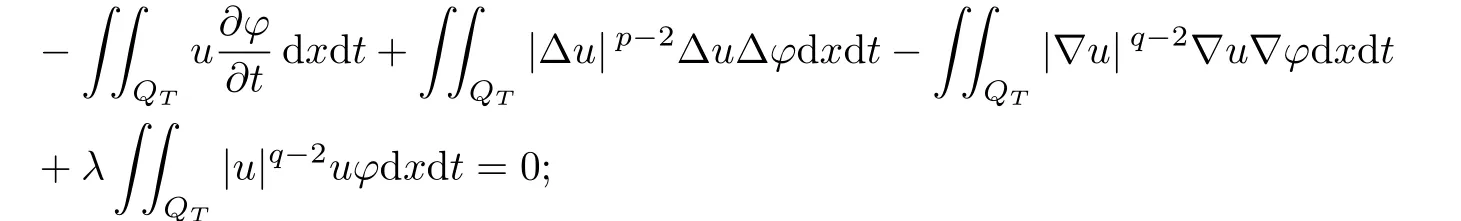
(3)u(x,0)=u0(x).
In this paper,we discuss the existence of weak solutions in Section 2.Our method is based on the discrete-time method to construct approximate solutions.By means of uniform estimates on solutions of the time-dif f erence equations,we prove the existence of weak solutions of the problem(1.1)–(1.3).Later on,we discuss the uniqueness of weak solutions in Section 3.
2 Existence of Weak Solutions
Theorem 2.1Let u0∈W2,p0(Ω).Then the problem(1.1)–(1.3)admits at least one weak solution.
To prove this theorem,we f i rst consider the following discrete-time problem:
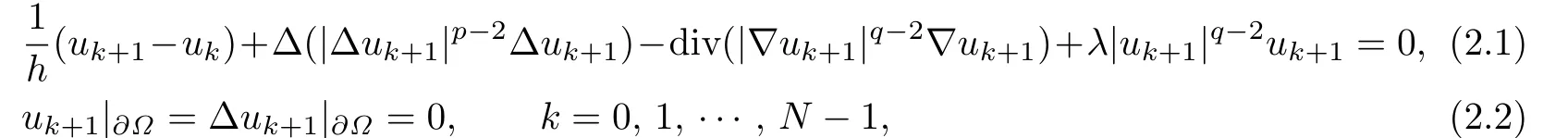
Lemma 2.1For any f i xed k,if,then the problem(2.1)–(2.2)admits a weak solution,such that for any(Ω),
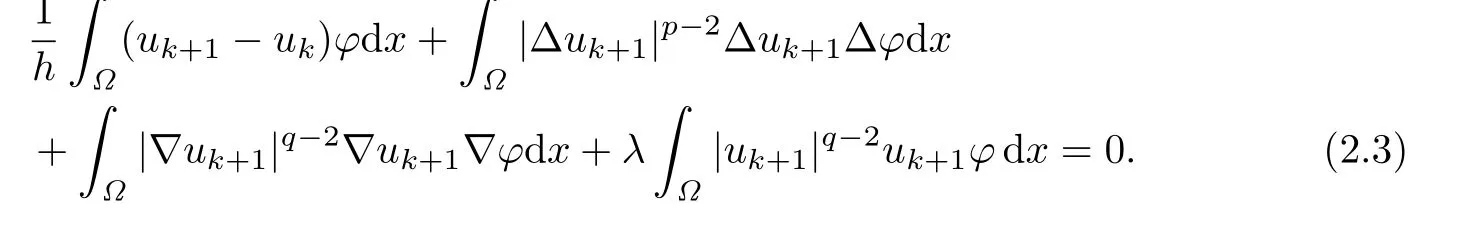
Proof.Consider the following functionals on
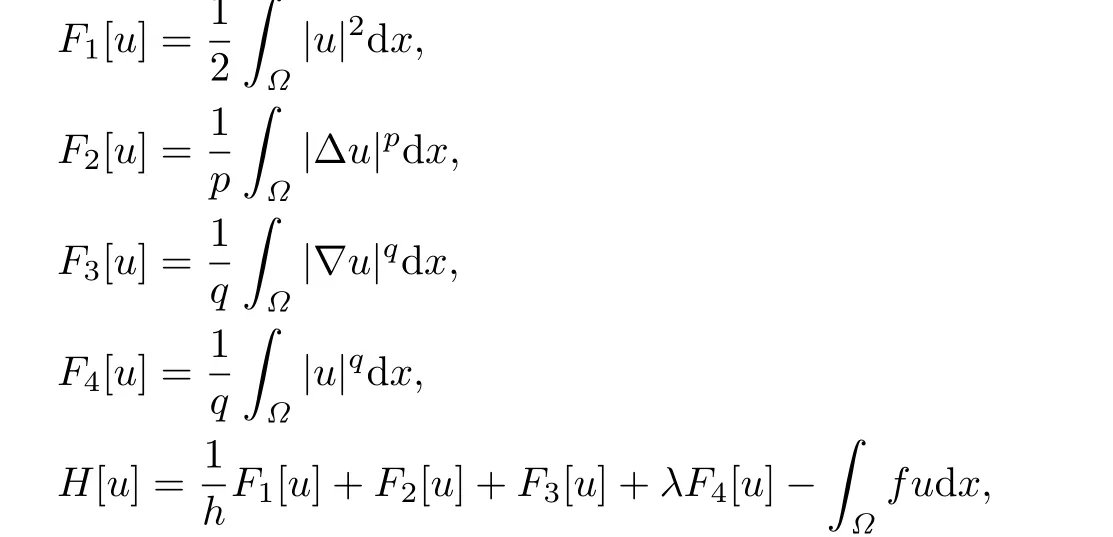
where f∈L2(Ω)is a known function.By the Young's inequality,we see that for C1>0,
∫
∫
∫
∫
∫
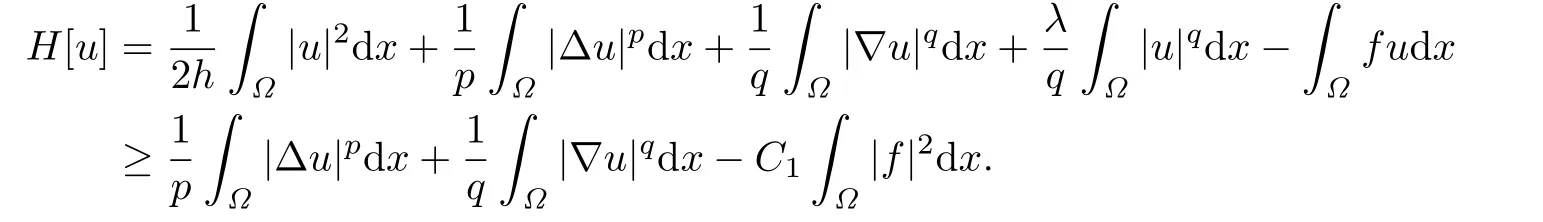
We need to check that H[u]satisf i es the coercivity condition.For this purpose,noticing that u|∂Ω=0 and using the Lptheory for elliptic equations(see[10]),we get
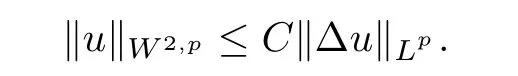
Therefore,H[u]→+∞as‖u‖W2,p→+∞.On the other hand,H[u]is clearly weakly lower semicontinuous onΩ).So,it follows from the results in[11]that there exists u*∈(Ω)such that
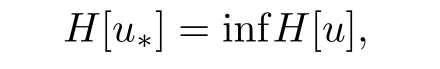
and u*is a weak solution of the Euler equation corresponding to H[u],namely,
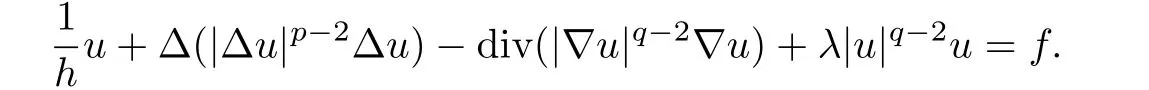
Choosing we get the conclusion of the lemma.The proof is completed.
Now,we construct an approximate solution uhof the problem(1.1)–(1.3)by def i ning
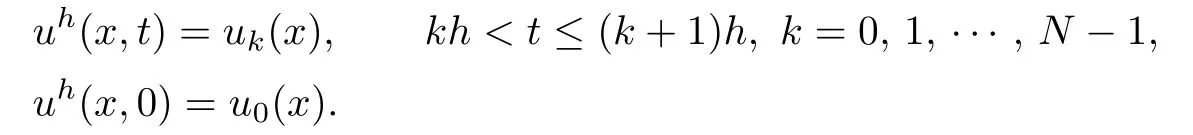
The desired solution of the problem(1.1)–(1.3)will be obtained as the limit of some subsequence of{uh}.For this purpose,we need some uniform estimates on uh.
Lemma 2.2For the weak solution ukof the problem(2.1)–(2.2),the following estimateshold:
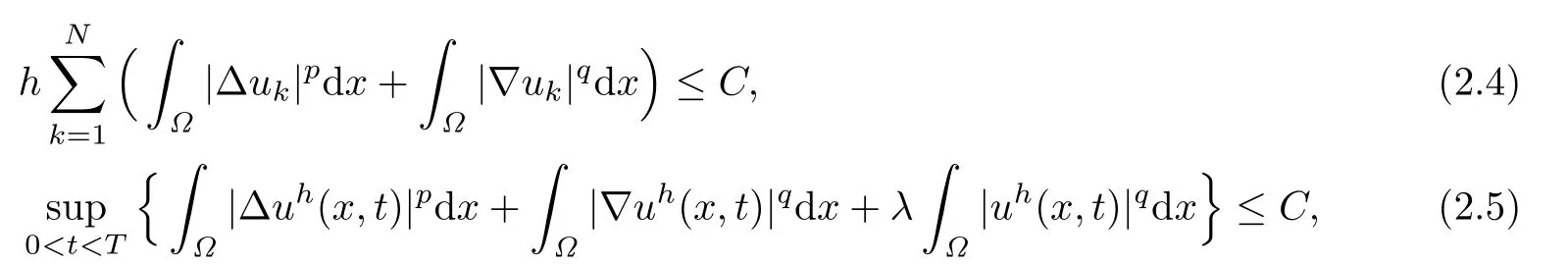
where C is a constant independent of h,k.
Proof.(i)We take φ=uk+1in(2.3)(we can easily prove that for φ∈W2,p0(Ω)(2.3)also holds)and obtain

Then by Young's inequality,we have
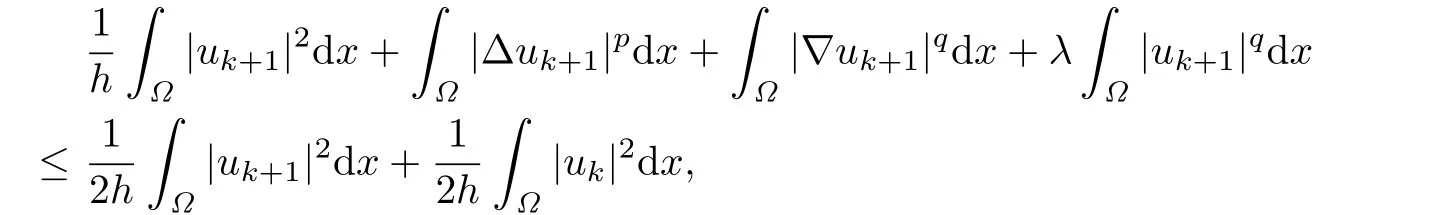
i.e.,

Summing up these inequalities for k from 0 to N-1,we have
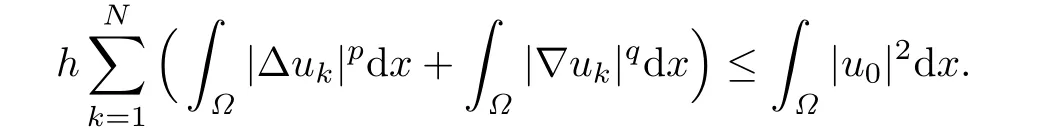
So(2.4)holds.
(ii)We choose φ=uk+1-ukin(2.3).Integrating by parts,we have
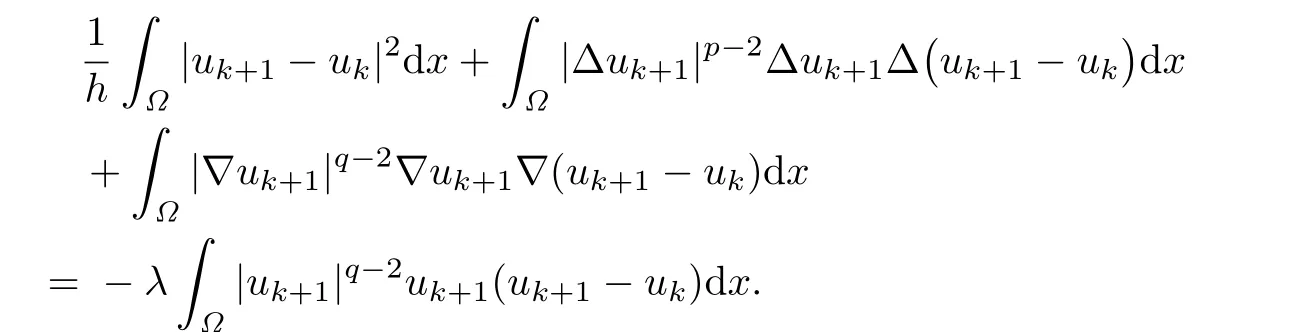
Since the f i rst term on the left hand side of the above equality is nonnegative,it follows that
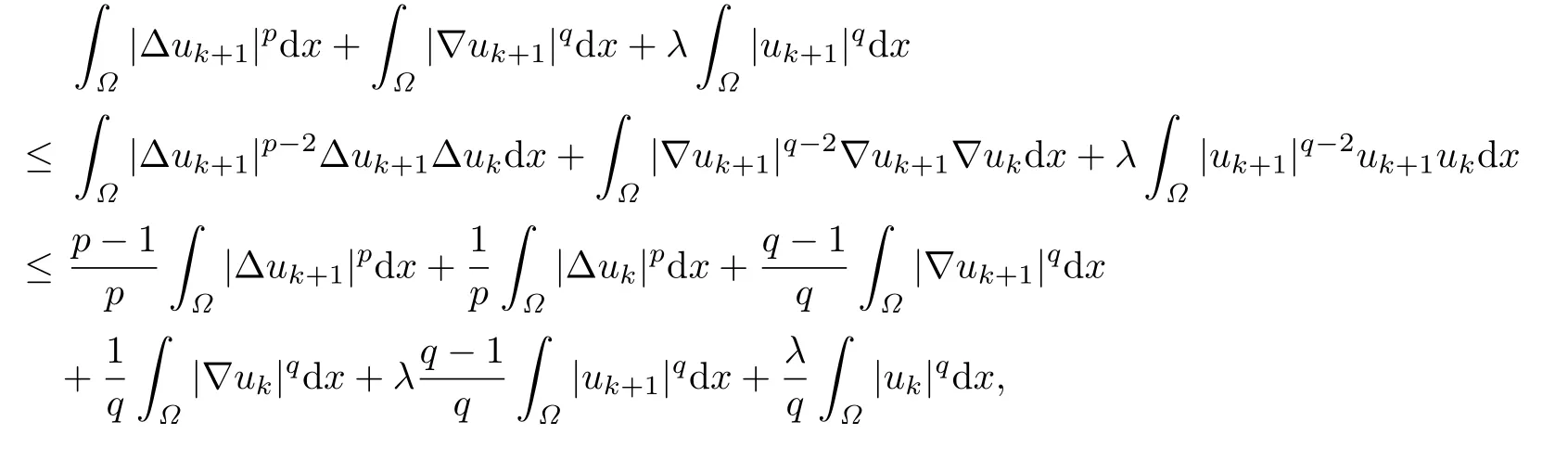
which implies that
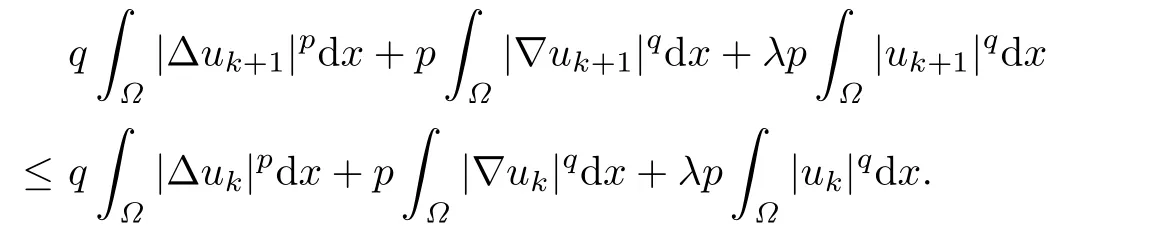
For any m with 1≤m≤N-1,summing up the above inequalities for k from 0 to m-1, we have
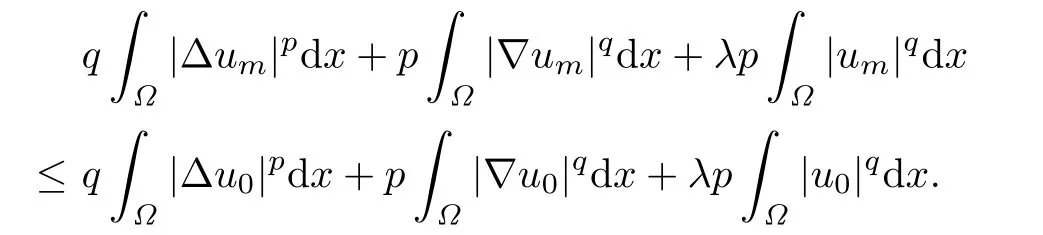
Since p>2 and q>2,we have
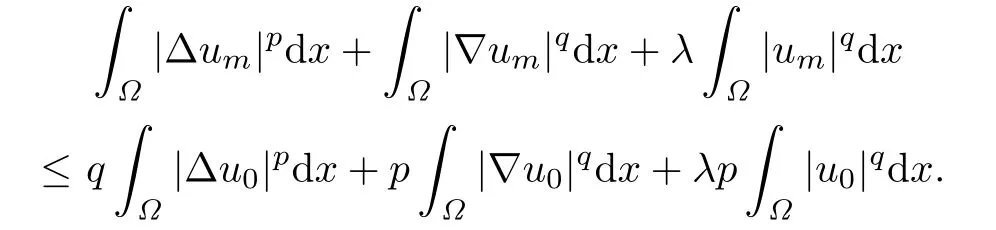
Hence(2.5)holds.The proof is completed.
Lemma 2.3Let uk+1be the weak solution of the problem(2.1)–(2.2).Then the following estimate holds:
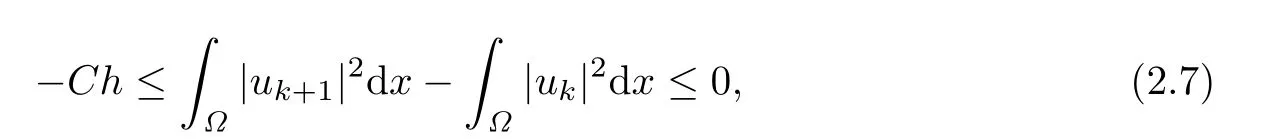
where C is a constant independent of h.
Proof.To prove the f i rst inequality,we choose φ=ukin(2.3).Integrating by parts and using the boundary condition,we have
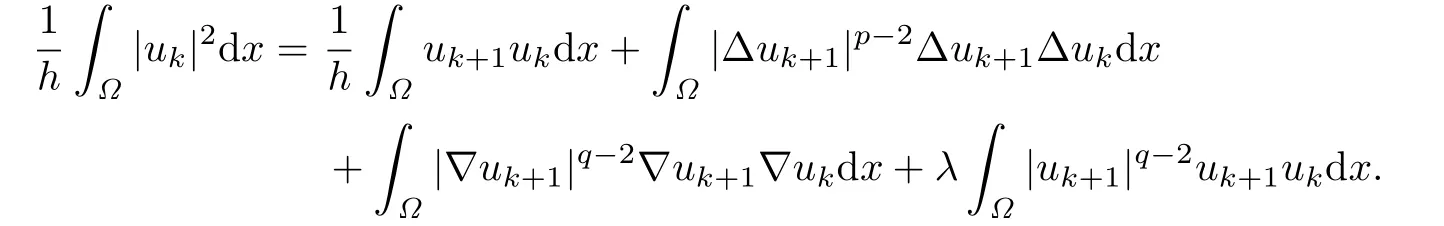
Applying Young's inequality and(2.5),we have
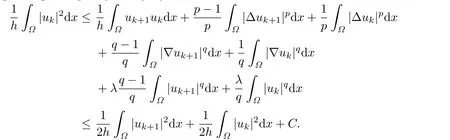
That is,
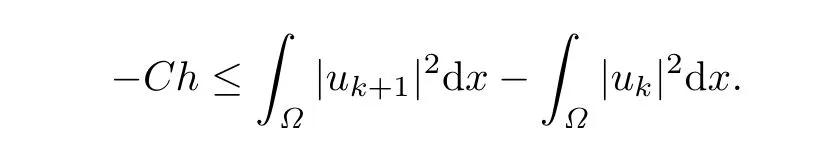
By(2.6)again,we have
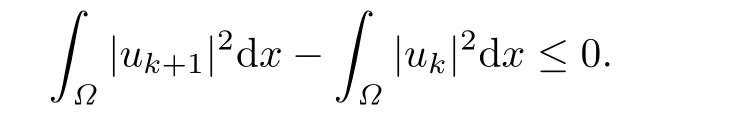
Proof of Theorem 2.1First we def i ne the operators Atand Bt,respectively by
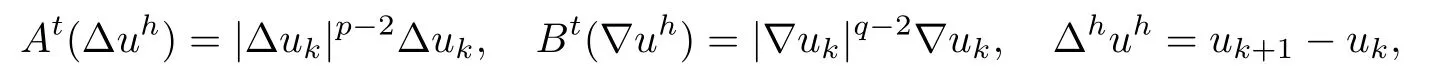
where kh<t≤(k+1)h,k=0,1,···,N-1.From(2.1)and(2.4),we see that
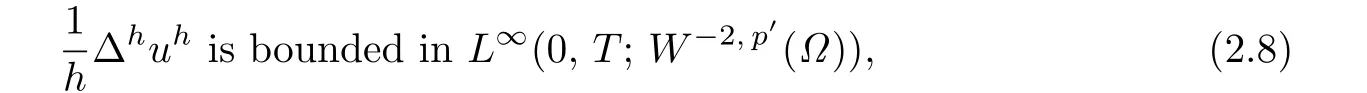
where p′is the conjugate exponents of p.By(2.3),(2.5),(2.8)and using compactness results (see[12]),we see that there exists a subsequence of{uh},which we denote as the original sequence,such that
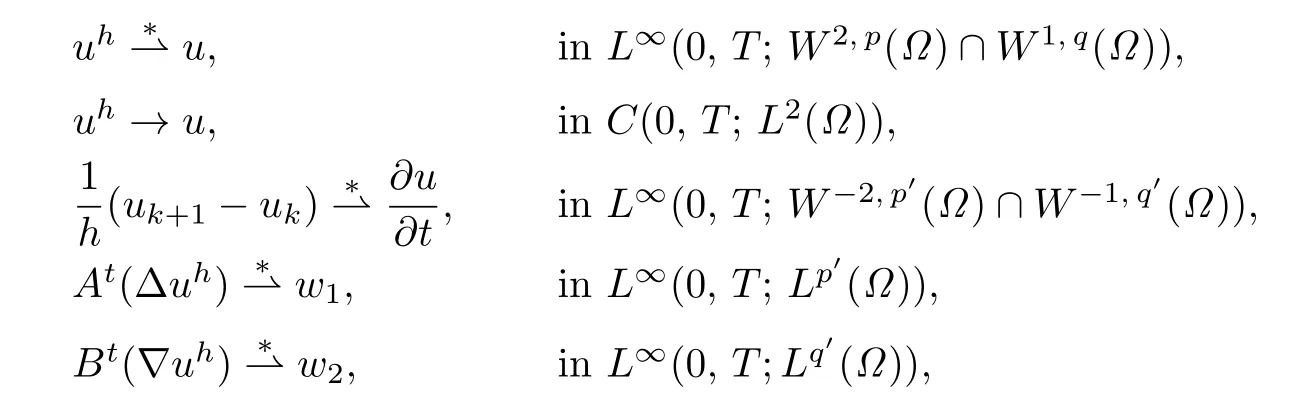
where p′and q′are the conjugate exponents of p and q,respectively.Then from(2.3),we see that,for any
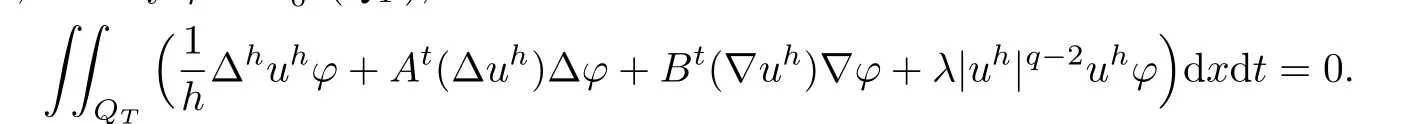
Letting h→0 yields
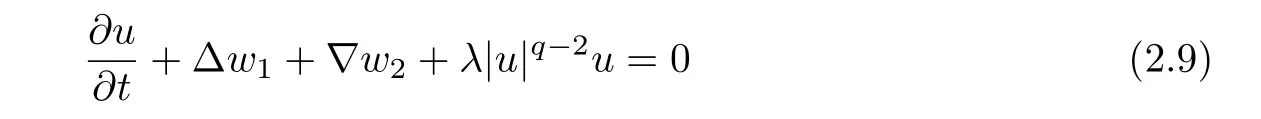
in the sense of distributions.
It remains to prove that
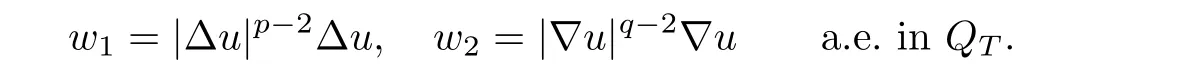
Set
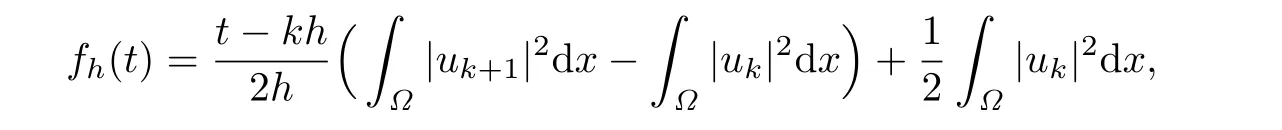
where kh<t≤(k+1)h,k=0,1,···,N-1.From(2.7),we have

and
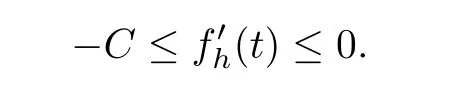
By the Ascoli-Arzela theorem,there exists a function f(t)∈C([0,T])such thaf(t)uniformly for t∈[0,T].From(2.7),we have

By(2.6)again,we have
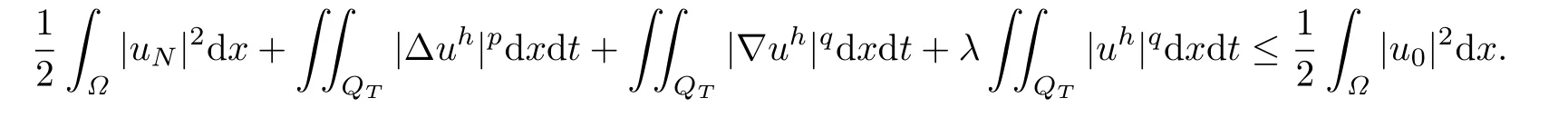
In the above inequality letting h→0,and using(2.10)we have
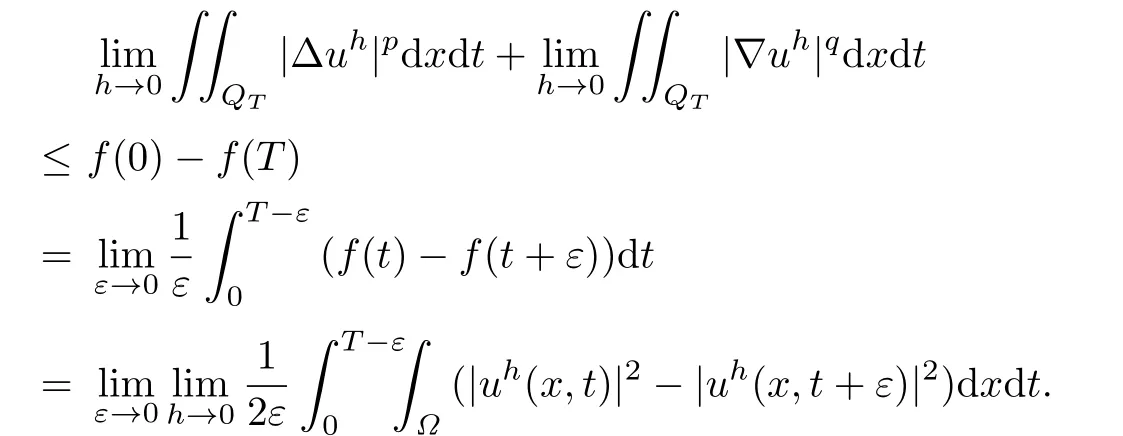
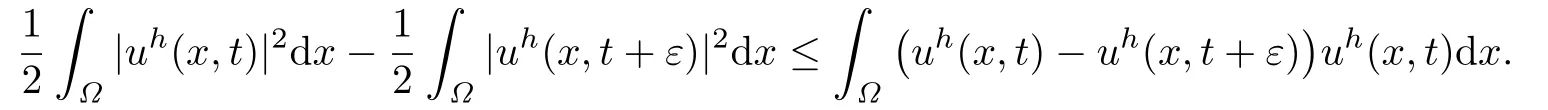
Therefore
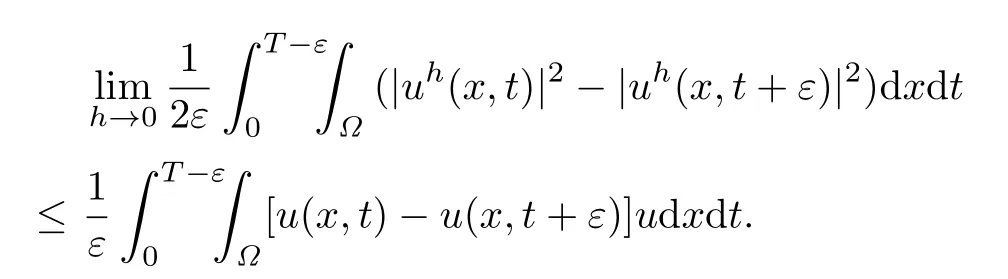
Hence,we obtain
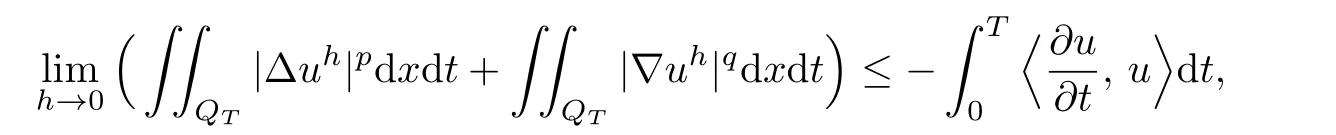
where〈·,·〉denotes the inner product.From(2.9),we have
Again by
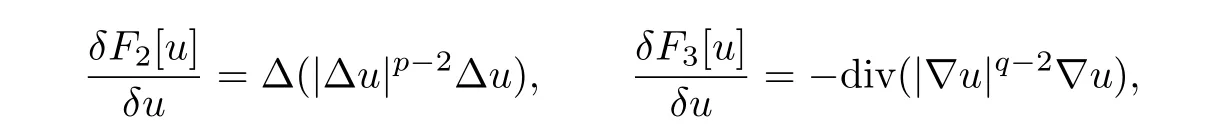
and convexity of F2[u]and F3[u],for anywe have
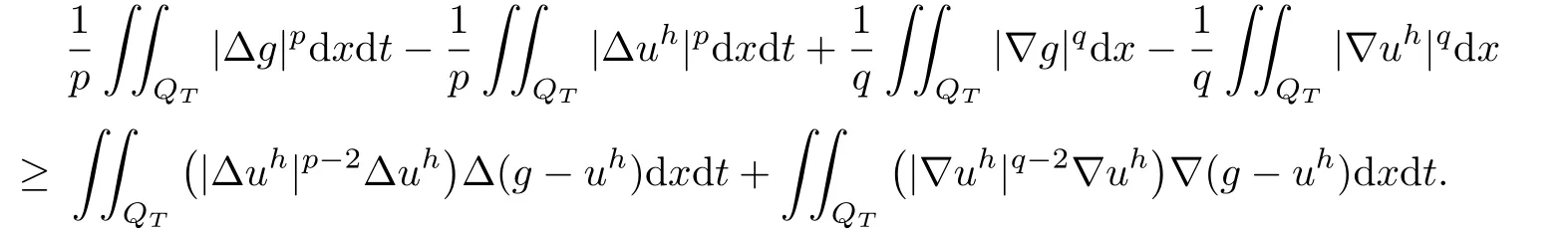
By(2.11)and the fact that F2[u]and F3[u]are weakly lower semicontinuous,letting h→0 in the above inequality,we have
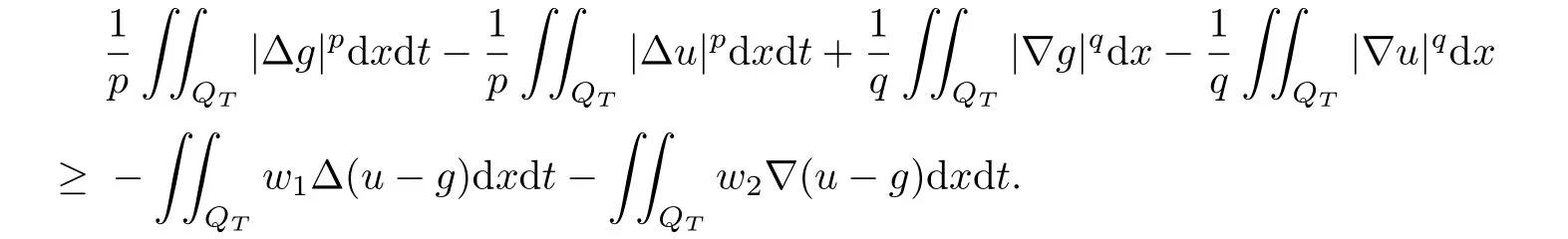
Replacing g by εg+u,we obtain

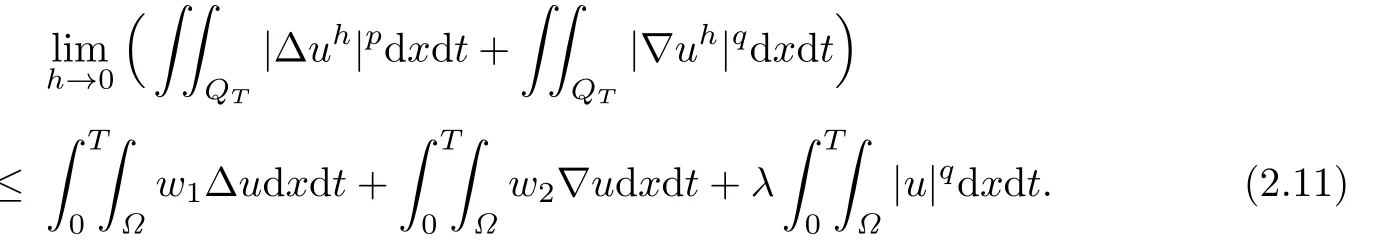
Letting ε→0 implies that
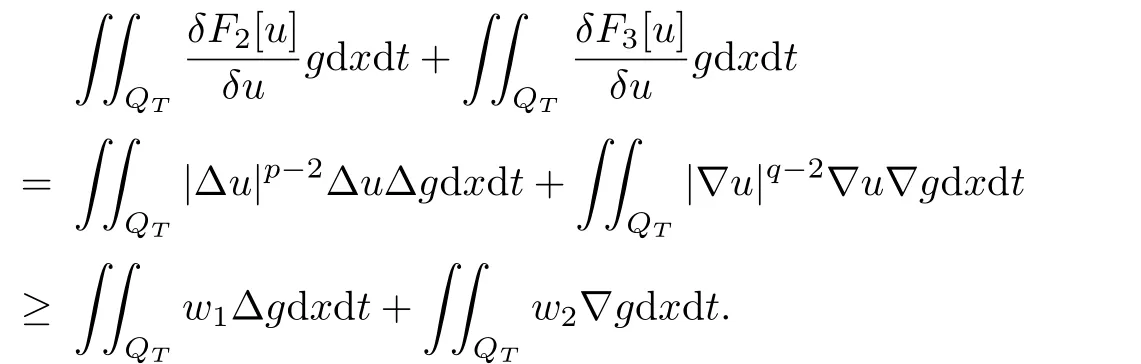
Due to the arbitrariness of g,we also get the opposite inequality to the above inequality. Therefore,

According to the strong convergence of uhin C(0,T;L2(Ω))and the fact that uh(x,0)= u0(x),it implies that u satisf i es the initial condition.
3 Uniqueness of the Solutions
In this section,we prove that the weak solution is unique.To this end we need the following lemma:
Lemma 3.1Forwith,0≤t1<t2≤T,the weak solutions u of the problem(1.1)–(1.3)on QTsatisf i es
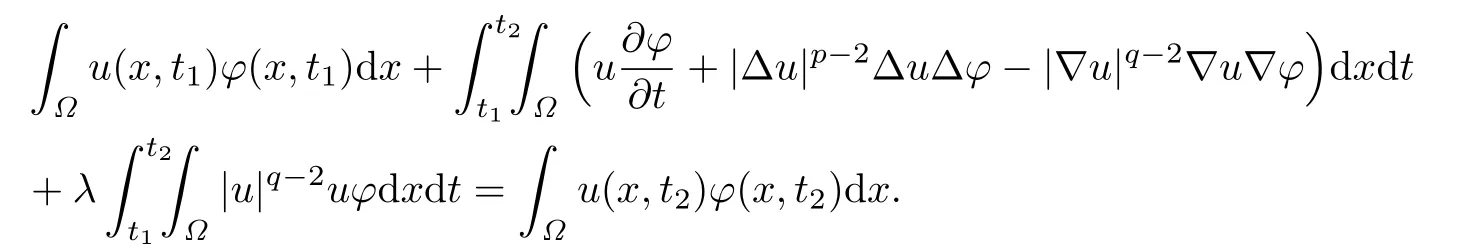
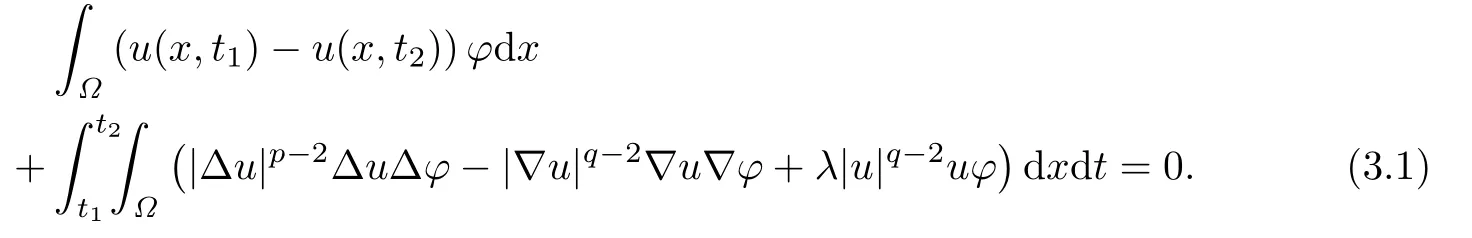
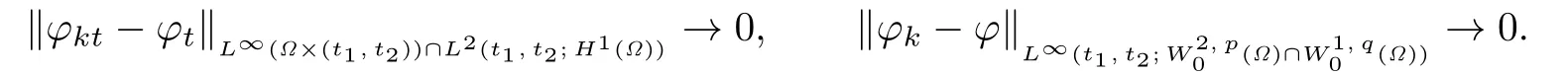
choosing φ=φk(x,t)η(t),we see that
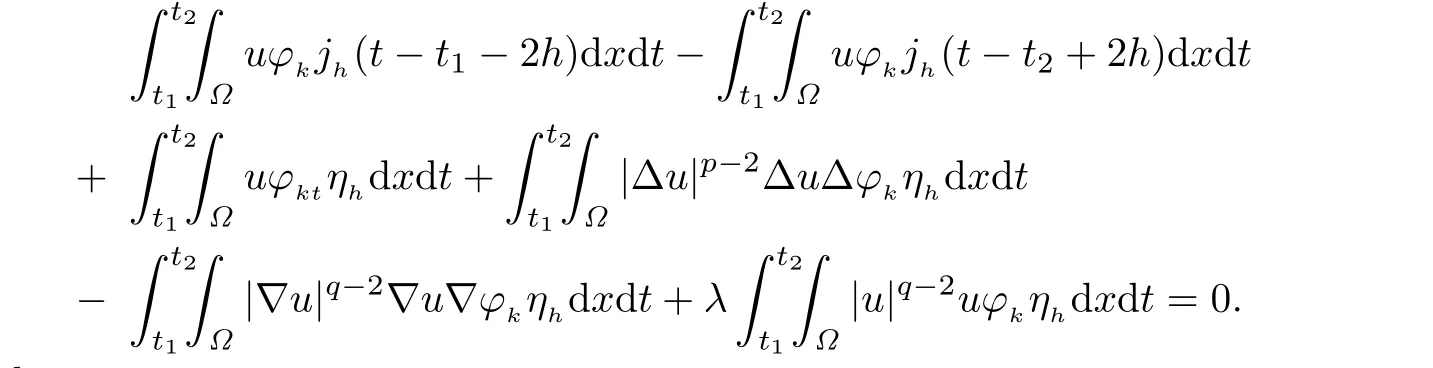
Observe that
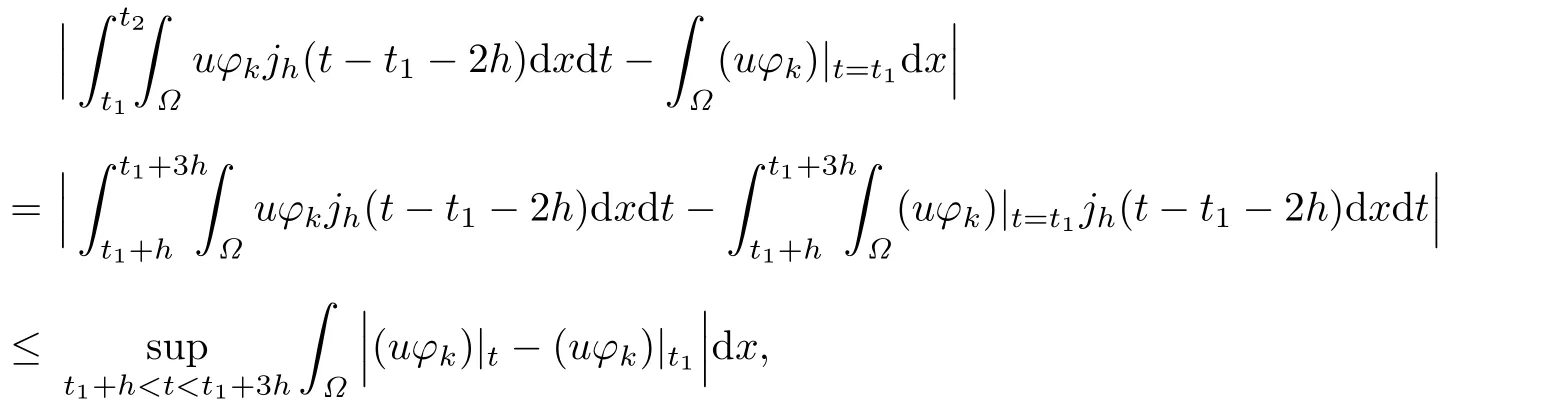
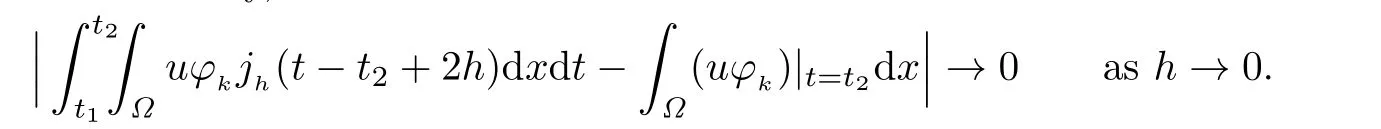
As h→0,k→+∞,we obtain

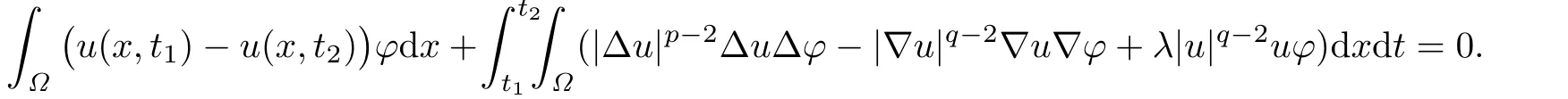
The proof is completed.
For a f i xed τ∈(0,T),set h satisfying 0<τ<τ+h<T.Let t1=τ,t2=τ+h.Then multiplying(3.1)by,for,we obtain
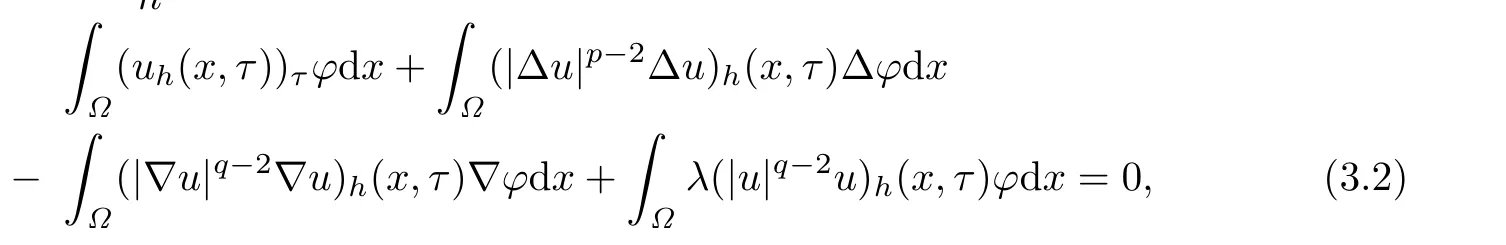
where
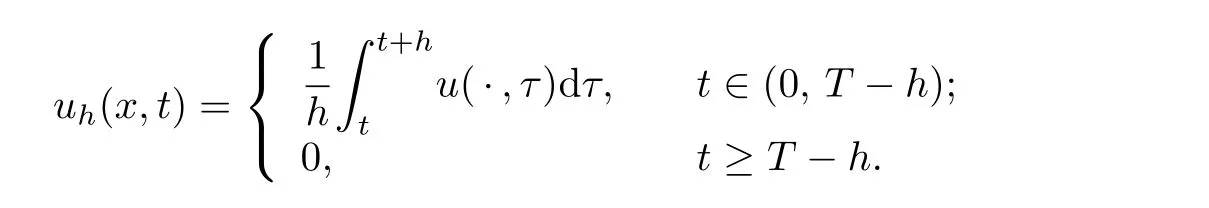
Theorem 3.1Let.The problem(1.1)–(1.3)admits only one weak solution.
Proof.Suppose that u1,u2are two solutions of(1.1)–(1.3).Then From(3.2),we have

∫
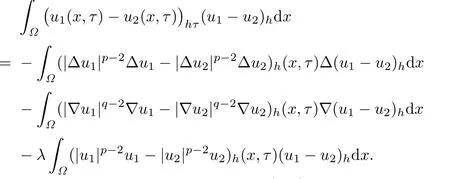
Integrating the above equality with respect to τ over(0,t),we have
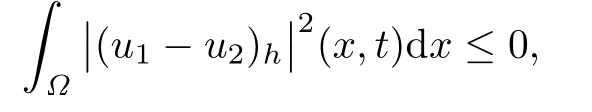
which implies that
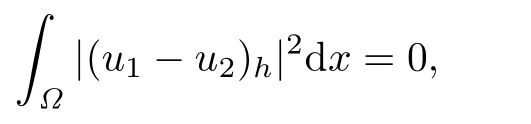
and therefore u1=u2.The proof is completed.
[1]King B B,Stein O,Winkler M.A fourth order parabolic equation modeling epitaxial thin f i lm growth.J.Math.Anal.Appl.,2003,286:459–490.
[2]Ortiz M,Repetto E A,Si H.A continuum model of kinetic roughening and coarsening in thin fi lm.J.Mech.Phys.Solids,1999,47:697–730.
[3]Zangwill A.Some causes and a consequence of epitaxial roughening.J.Crystal Growth,1996, 163:8–21.
[4]Liu C,Du Y.Existences of radial solutions for a fourth order parabolic equation.Comm.Math. Anal.,2008,5:44–56.
[5]Mullins W.Theory of thermal grooving.J.Appl.Phys.,1957,28:333–339.
[6]Cahn J,Taylor J.Surface motion by surface dif f usion.Acta.Metall.Nater.,1994,42:1045–1063.
[7]Grinfeld M,Novick-Cohen A.The viscous Cahn-Hilliard equation:Morse decomlosition and structure of the grobal attractor.Trans.Amer.Math.Soc.,1999,351:2375–2406.
[8]Barrett J W,Blowey J F.Finite element approximation of the Hahn-Hilliard equation with concentration dependent mobility.Math.Comp.,1999,68:487–517.
[9]Cohen D S,Murrey J D.A generalized dif f usion model for growth and dispersal in a population. J.Math.Biology,1981,12:237–249.
[10]Chen Y,Wu L.Second Order Elliptic Equations and Elliptic Systems(in Chinese).Beijing: Scince Press,1991.
[11]Chang K.Critical Point Theory and Its Applications(in Chinese).Shanghai:Shanghai Sci. Tech.Press,1986.
[12]Simon J.Compact sets in the space Lp(0,T;B).Ann.Mat.Pura Appl.,1987,146:65–96.
A
1674-5647(2013)03-0261-10
Received date:Jan.5,2012.
E-mail address:lzszgjy@126.com(Guo J Y).
2000 MR subject classif i cation:35D05,35G30
杂志排行
Communications in Mathematical Research的其它文章
- On the Nonlinear Matrix Equation X+A*f1(X)A+B*f2(X)B=Q
- Efficient Mean Estimation in Log-normal Linear Models with First-order Correlated Errors
- A Family of Fifth-order Iterative Methods for Solving Nonlinear Equations
- Modelling the Spread of HIV/AIDS Epidemic
- The Centres of Gravity of Periodic Orbits
- The Supersolvable Order of Hyperplanes of an Arrangement
