一种在FPGA上实现的FIR滤波器的资源优化算法

曲仕茹，彭纪昌

（西北工业大学 自动化学院，陕西 西安 710072）

随着数字化通信技术的快速发展，高质量的信号处理对滤波器的性能和资源占有量提出了更高的要求。数字滤波器是数字信号处理中的一个重要模块，FIR滤波器作为最常用的滤波器广泛用在实时信号的处理中。FIR滤波器分为软件和硬件两种实现方式。软件采用计算机的储存器计算器把滤波器的运算编成程序通过计算机来执行。硬件一般采用时域卷积的方法实现[1]。

目前较为常用的FIR滤波器结构主要有，直接结构、转置型结构和分布式算法的结构。直接结构的滤波器设计方法是将滤波运算转化为乘积的累加；转置结构的滤波器设计方法与直接结构的滤波器相比，采用简化加法图（RAG）和流水线技术；分布式算法（DA）是一种重要的FPGA技术，广泛地应用在计算乘积和的过程中。直接结构的设计方法没有考虑到系数之间的关系，芯片面积较大，计算速度不高。采用RAG算法的流水线结构的滤波器较采用DA结构的滤波器在逻辑资源消耗上有一定减少，并节约的芯片的尺寸，不过在计算速度上稍慢于DA结构的滤波器，但是其消耗逻辑资源总量/最高速度明显要优于DA结构[2]。因此基于RAG算法结构的滤波器设计能较好的满足设计要求。

1 FIR滤波器原理和结构

数字滤波器通常用于修正或改变时域或频域中信号的属性。最为普通的数字滤波器就是线性时不变（Linear Time-Invariant，LTI）滤波器。LTI数字滤波器通常分成有限脉冲响应 （Finite pulse Response，FIR）和 无 线 脉 冲 响 应 （Infinite Impulse Response，IIR）两大类。带有常系数的FIR滤波器是一种LTI数字滤波器。L阶的FIR输出对应于输入时间序列x[n]的关系由一种有限卷积和的形式给出：

其中f[0]≠0一直到f[L-1]≠0均是滤波器的L阶的系数，同时它们也对应于FIR的脉冲响应。

FIR滤波器由一个“抽头延迟线”加法器和乘法器的集合构成，给每个乘法器提供的其中一个操作数就是一个FIR系数。FIR滤波器从结构上可以分为直接型和转置型。

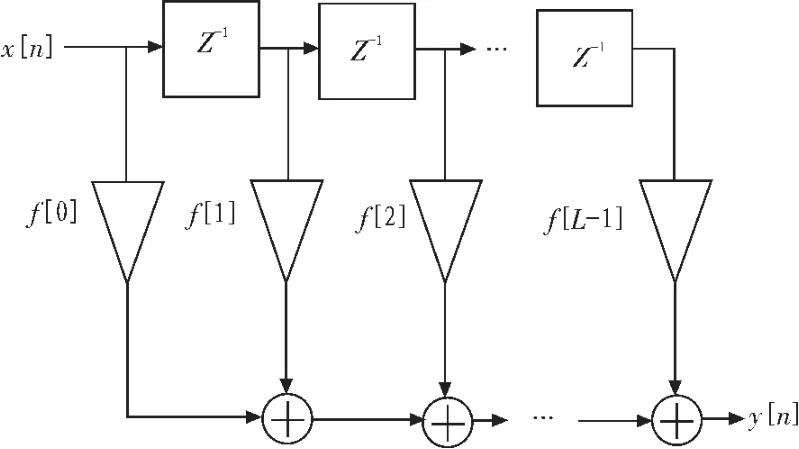
图1 直接型结构Fig.1 Direct structure filter

图2 转置型结构Fig.2 Transposition structure filter

由于FIR滤波器总是线性相位的，其单位脉冲响应是序列是 f（n），且满足 f（n）=± f（L-1-n）。 线性相位 FIR 的固有对称属性可以降低所需要的乘法器数量，如图3所示。可以看到“对称”体系结构在每个滤波器周期正好是图1给出的直接体系结构的一半（L比L/2），而加法器数量保持不变（L-1）。

图3 线性相位结构Fig.3 Linear phase structure filter

FIR滤波的过程就是一个信号逐级延迟的过程，将各级延迟的输出信号加权并累加既得FIR滤波器的输出，这其中最重要的运算就是乘累加运算。FIR滤波器每完成一次滤波需要进行L次的乘法运算和L-1次的加法运算，FIR滤波器的运算量取决于L的大小[3-4]。

2 基于DA算法的FIR滤波器原理

当滤波器的阶数较高时乘累加式结构的滤波器已经不能满足实时性的要求并且会消耗过高的逻辑资源。这是就需要使用基于分布式算法DA（Distributed Arithmetic）的滤波器结构。分布式算法最初是在1973年Croisier的论文中被提出来的，后又经Peled等人的推广演绎，但直到FPGA出现并迅速发展时，才在应用领域得到广泛应用[5]。

一个L阶FIR滤波器表达式如下：

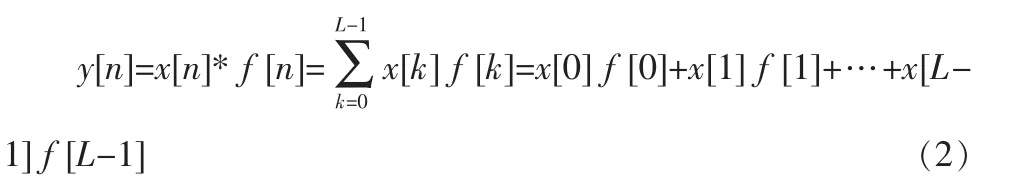
其中，y（n）表示滤波器的输出，x（n）表示滤波器的输入，f（n）表示滤波器的系数，L表示滤波器的阶数。在FPGA中，数据采用二进制的补码表示，所以有符号的输入信号x（n）表达式如下：

其中，xb[n]表示 x[n]的第 b位，而 x[n]也就是 x的第 n次采样，而输出y的表达式为：

图4 基于DA算法的滤波器结构Fig.4 DA structure filter

3 改进的资源优化算法FPGA上的实现

基于DA算法的FIR滤波器可以提高运算速度，但是同时会消耗更多的逻辑资源。简化加法器图 （Reduced Adder Graph，RAG）算法在降低滤波器的逻辑资源的同时也能提高运算速度。RGA算法在硬件上只需加法和移位方法实现乘法，并利用各系数之间的相关性，最大程度的减少加法器个数和加法次数，因为移位不消耗资源，所以整个设计的硬件开销只是加法器的个数[6]。

如系数13和45，根据RAG算法可以表示为5图。需要3个加法器和3次移位就可以计算出常系数13和45的乘法。

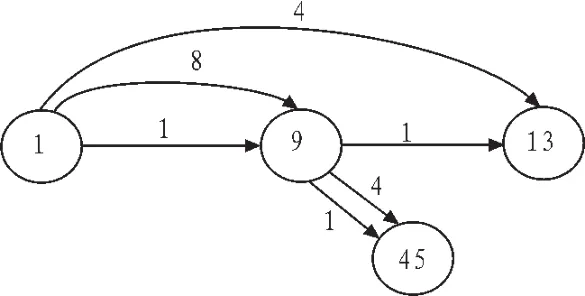
图5 使用RAG算法实现常系数Fig.5 Use RAG algorithm generation constant coefficient

RAG算法的基本步骤：

1）将输入集合中的所有系数简化成正数

2）查表计算每个系数的单系数加法器成本

3）删除系数集合中所有2的幂和重复的系数

4）找出实现只需要一个加法器的系数

5）检查是否有一个系数可以用一个加法器和以实现的系数实现

6）重复步骤5，直到没有系数添加到图集中为止

7）使用已有的或新的非输出单元实现需要两个加法器的小系数

8）重复步骤5直到没有新的系数加入加法图

9）使用已有的或者新的非输出单元实现需要三个加法器的小的系数

10）返回步骤5，直到所有系数都已合成好[7-10]

FIR滤波器的设计利用Matlab中的FDA Tool工具，设计一个16阶，Fs=48 kHz，Fc=10.8 kHz的FIR滤波器。FPGA实现中采用经量化取整的滤 波系数 {-9，3，14，1，-22，-12，46，106，106，46，-12，-22 ，1，14，3，-9}。

图6 FIR滤波器的幅值和相位响应Fig.6 Amplitude and phase response of FIR filter

由于FIR滤波器的系数具有对称性，这里只讨论C0到C7的RAG实现过程。该系数实现所有的滤波器系数只需要6个加法器以及移位运算，节省了大量的逻辑资源[7]。

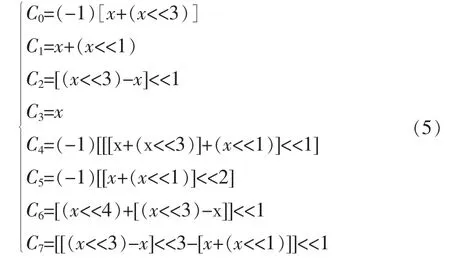
如图7所示RAG结构的滤波器仅需要6个加法器以及9次移位操作就可以实现所有的滤波器系数。节省了大量的逻辑资源。

图7 滤波器系数的RAG实现Fig.7 Realization of the filter coefficients by RAG algorithm

FIR滤波器的FPGA实现与仿真，在Quartus II平台中进行试验，选用 Cyclone II系列的EP2C35F672C6器件，用VerilogHDL语言设计RAG算法结构并用SignalTap II对其进行仿真。仿真结果如图8所示。clk为时钟信号，d_in为输入信号，dout_ly为理论输出值，dout为滤波器输出。

图8 滤波器仿真波形Fig.8 Simulation waveforms of Filter

可以从仿真结果看出滤波器的滤波效果还是非常理想的并且滤波的速度也相对较快。工业界广泛使用的DSP Builder生成的分布式算法滤波器性能作为滤波器的参考标准[11-12]。本文采用RGA算法实现的滤波器与同等规模的DSP Builder生成的滤波器的IP核在相同的FPGA平台上实现后比较的到的结果如表1所示。可以看到基于RAG算法的滤波器在逻辑资源节省上有了很大的提升。

表1 滤波器占用资源对比Tab.1 Filter resource comparison

4 结 论

本文通过使用RAG算法设计了线性相位的低通滤波器。通过仿真验证了该滤波器的可行性，满足设计要求。基于其结构的特征，在硬件实现上采用了转置结构设计该滤波器，使用RAG算法实现所有系数乘积综合，最大程度的减少加法器的数量，使用移位运算代替乘法器结构，并使用流水线的技术提高运行速度。仿真实验表明基于RAG算法了滤波器比DA算法要节省大量的逻辑资源，满足高速处理要求。以设计一个16阶滤波器为例，在Altera公司QuartusⅡ的环境下采用VerilogHDL硬件描述语言进行设计实现并采用SignalTap II进行仿真验证，在此基础上进行性能分析，实验结果证实了此种设计方法在解决速度和面积矛盾方面的优势。

[1]U.Meyer-Baese Digital Signal Processing with Field Programmable Gate Arrays[M].3rd ed.New York:Springer Berlin Heidelberg，2007.

[2]Tan L，Jiang J.Adaptive volterra filters for active control of nonlinear noise processes[J].IEEE Transactions on Signal Processing，2001，49（8）:1667-1676.

[3]Mirzaei S，Hosangadi A，Kastner R.FPGA implementation of high speed FIR filters using add and shift method[C].International Conference on Computer Design.Las Vegas，Nevada， USA，2006.

[4]DENG Tian-Bo.Design and parallel implementation of FIR digital filters with simultaneously variable magnitude and non-integer phase-delay[J].IEEE Analog and Digital Signal Processing，2003，50（40）:243-250.

[5]Zhu W，Zhang G M，Zhang Z M.Design of FIR filter based on distributed algorithm with parallel structure[J].Journal of Electronic Measurement and Instrument，2007（21）:87-92.

[6]李莹，路卫军，于敦山，等.一种在FPGA上实现FIR数字滤波器的资源优化算法[J].北京大学学报：自然科学版，2009，45（2）:222-226.LI Ying，LU Wei-jun.A resource optimizing algorithm in FPGA based high speed FIR digital filters[J].Acta Scientiarum Naturalium Universitatis Pekinensis，2009，45（2）:222-226.

[7]夏宇闻.Verilog数字系统设计教程[M].北京:北京航空航天大学出版社，2008.

[8]XIE Jia-feng，HE Jian-jun，TAN Guan-zheng.FPGA realization of FIR filters for high-speed and medium-speed by using modifieddistributedarithmeticarchitectures[J].Microelectronics Journal，2010（41）：365-370.

[9]MEYER U.Digital signal processing with field programmable gate arrays[M].3rd ed.New York:Springer Berlin Heidelberg，2007.

[10]HAN Jeong-Ho，PARK In-Cheol.Digital Filter Synthesis Considering Multiple Adder Graphs for a Coefficient[C]//IEEE Computer Design，ICCD 2008:315-320.

[11]吴伟，唐斌.可变带宽FIR数字滤波器的高效加权最小二乘设计及实现[J].仪器仪表学报，2008，29（3）:550-555.WU Wei，TANG Bin.Efficient weighted-least-square design and realization of FIR digital filters with variable bandwidth[J].ChineseJournalofScientificInstrument，2008，29（3）:550-555.

[12]Wirthlin M J.Constant coefficient multiplication using look-up tables[J].Journal of VLSI Signal Processing，2004，36（1）:7-15.