基于能量获取的小型无人机飞行控制研究

夏露，胡荣华，商重阳

(西北工业大学翼型叶栅空气动力学国家重点实验室，陕西西安710072)

0 引言

小型无人机由于自身所携带能量(燃油、储电等)有限而不能进行长时间飞行，同时小型无人机由于其本身的低雷诺数性质而对其飞行性能有所影响。但是，通过观察发现，有些大型鸟类比如秃鹫等可以通过对上升气流的利用而达到持续飞行数百公里的目的。有经验的滑翔机驾驶人员可以借助合适的上升气流来达到增加飞机航程航时的目的［1］。

针对上述现象，本文以小型电动无人机为例探讨如何利用大气扰动中的能量来增加航程航时。为了对风场的利用情况进行评价，采用飞行单位距离的能量消耗作为评价标准，为此，建立小型无人机在风场中飞行时的能量高度方程，在满足动力学条件以及飞行参数约束条件下得到能量消耗最少所对应的飞行参数(优化状态)，并据此设计相应的控制律，使飞机尽可能在优化状态下飞行，以达到利用风场进行飞行的目的。

1 动力学以及运动学方程

为了简化起见，本文只考虑纵向问题。利用质点模型建立飞机在大气扰动中的运动学和动力学方程［1-2］，参考坐标系如图1 所示，Si，Sb，Ss分别表示惯性坐标系、机体坐标系以及气流坐标系 (稳定性坐标系)。飞机的运动学方程可表示为空速、航迹倾角以及风速的函数:

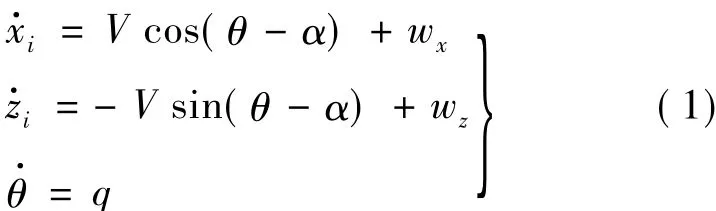
在稳定坐标轴系下以空速、迎角表示的飞行器动力学方程为:

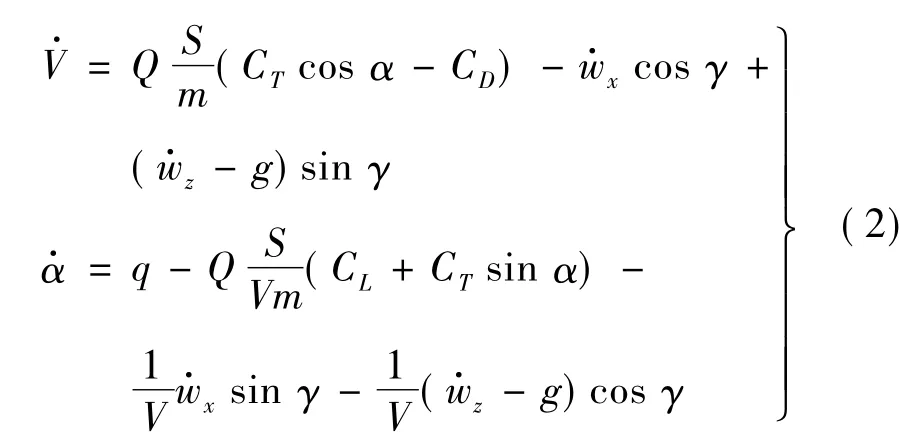
式中，wx，wz分别为风速在惯性坐标系上的分量;w·x，w·z分别为风速加速度在惯性坐标系上的分量;航迹倾角γ=θ－α;动压Q=ρV2/2。

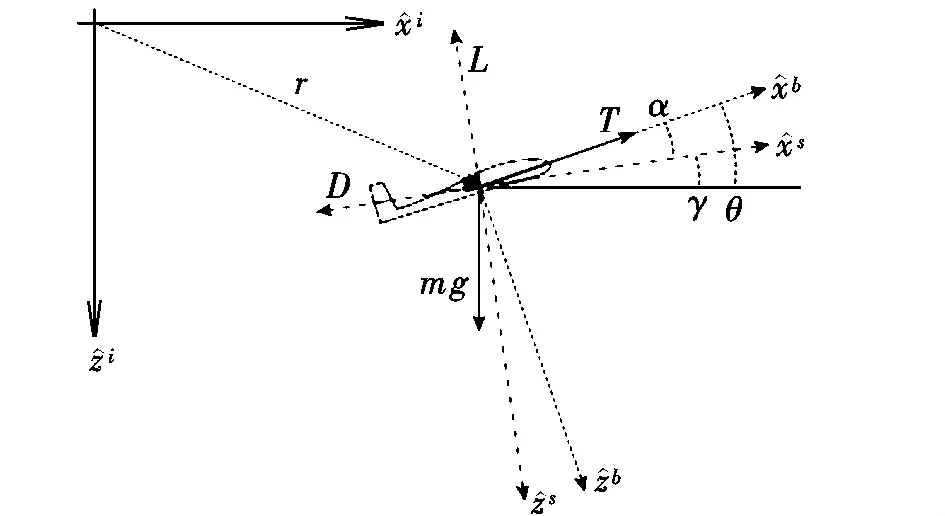
图1 参考坐标系Fig．1 Reference coordinate system

2 能量方程

定义飞机机械能为:

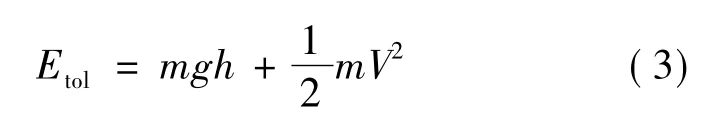
在整个飞行过程中设定小型电动无人机质量保持不变，定义能量高度为:

因此，能量相对时间的变化率为:

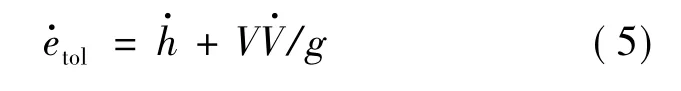
代入动力学方程(2)可得:

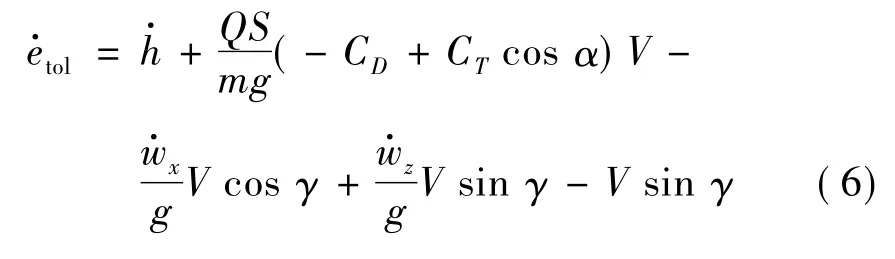
由于h·=－z·=V sinγ－wz，可以得到:

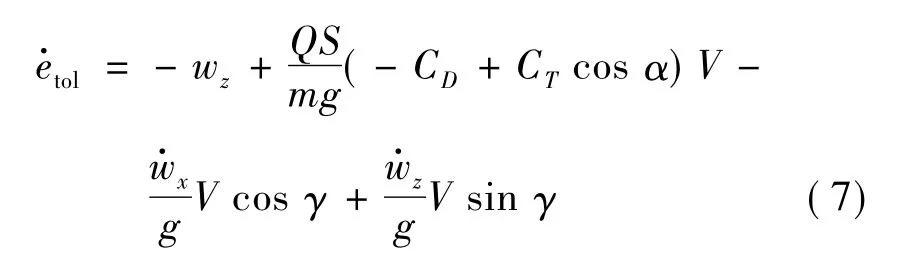
3 优化模型

3.1 目标函数

能量获取问题相当于如下轨迹优化问题:

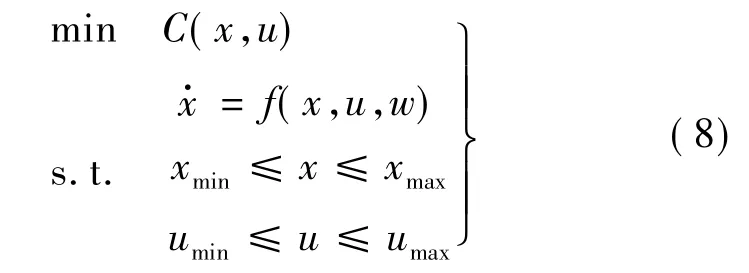
约束条件中的第一项表示运动学方程以及动力学方程的约束;第二项表示状态量的约束;第三项表示控制输入量的约束。

根据任务需要的不同，目标函数的选择相差较大［3］，本文优化目标是飞行单位距离的能量消耗最少:即最大化Δe/Δx。在没有大气扰动的情况下，Δe/Δx一直为负，在有动力飞行时表现为机载能量的消耗。基于本文的研究目的，在进行能量优化时，不考虑发动机运动产生的能量，采用的目标函数如式(9)，设计变量包括空速、迎角以及俯仰角:

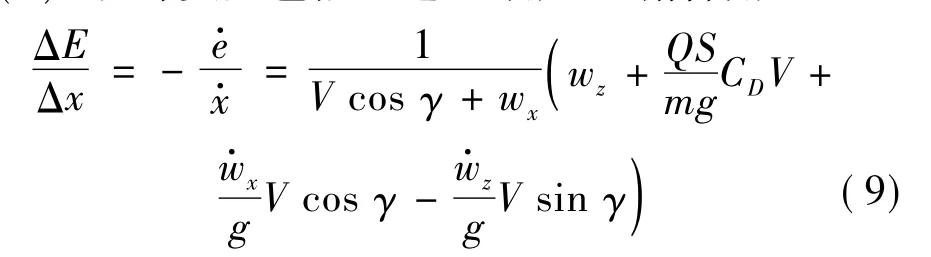
3.2 优化模型求解

本文只考虑纵向问题，优化模型中涉及到的飞行参数包括空速、俯仰角以及迎角;纵向控制输入量包括升降舵偏角δe以及发动机推力系数δT，但是通过δe和δT难以同时达到对这几个参数的精确控制，本文通过引入平衡条件的方式来达到减少控制量的目的。

3.2.1 定常直线飞行状态

假定飞机以定常直线状态飞行，此时切向力和法向力平衡，满足如下所示的力平衡关系［1］:

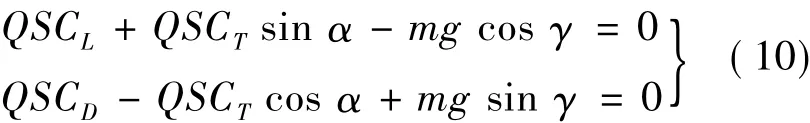
由上式可知:

假设航迹倾角γ很小，则sinγ≈γ，cosγ≈1，由于在定常直线状态飞行，迎角较小并且推力系数相对于升力系数而言是个小量，所以CTsinα相对于CL是个小量，在此忽略不计，进一步可以得到升力系数与空速之间的近似关系式:

不考虑升降舵偏转对升力、阻力的影响，升力和阻力只是迎角的函数;整个飞行阶段发动机功率保持不变，在一定高度下CT是空速V的函数，目标函数可转化为只与空速相关的函数。

3.2.2 直线飞行状态

上节中假设飞机以定常直线状态飞行，但是飞机不一定能够在这种状态下飞行，因此为了弱化约束，假定飞机迎角和俯仰角保持不变(也就是只保持法向处于力平衡状态)，此时速度大小仍然可能在变化，通过式(2)可以得到:

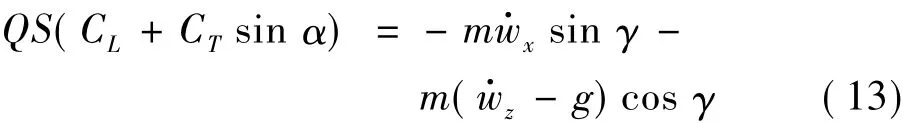
引入式(13)作为式(9)的补充函数，通过在Matlab中调用fmincon函数求解带约束的多变量优化问题方法来得到优化状态飞行参数。

4 控制律设计

能量获取结构流程如图2所示，根据当前风场特性结合优化模型计算出相应的纵向飞行参数xopt，在优化状态计算出来后，针对本文的研究问题进行纵向控制律设计［4］。

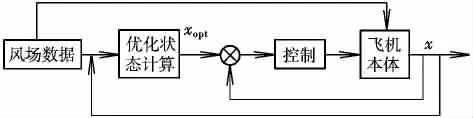
图2 能量获取流程图Fig．2 Flow chart of energy extraction

采用的控制律形式如下:

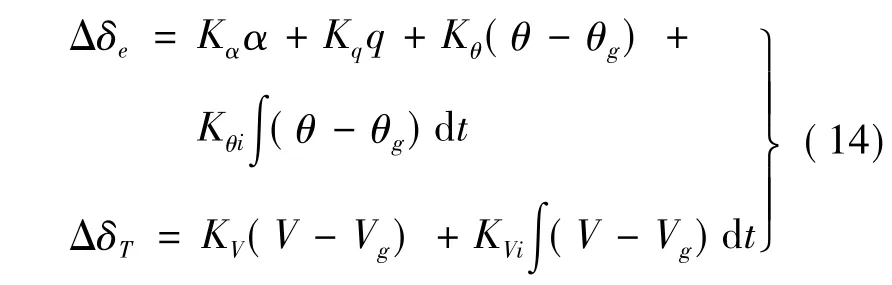
其中，引入迎角和俯仰角速度反馈是为了增加飞机的稳定性。采用经典根轨迹法通过时域频域调参，最终选择的一组控制律参数如下:

Kα=0.005 1，Kq=0.25，Kθ=0.168

Kθi=0.025，KV=3，KVi=0.1

5 仿真分析

在平稳大气中，为了达到最大航程飞机应该在最大升阻比状态下飞行。本文选择最大升阻比状态为基准状态，所有仿真的初始飞行条件保持一致，采用的控制律一致。

5.1 上升热气流

假设风场特性已知，对于单个的上升热气流，本文采用Gedeon提出的垂直风速的风模型(仿真曲线见图 3)［5］:

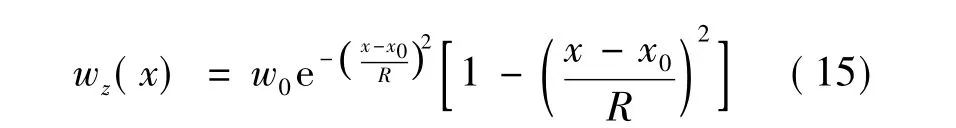
式中，w0为垂直方向的最大风速;x0为上升热气流的中心;R为热气流的作用半径。仿真过程中上升热气流半径为R=100～300 m，能够达到的最大风速为3 m/s。对于N个上升热气流来说，总的垂直方向的风速为:

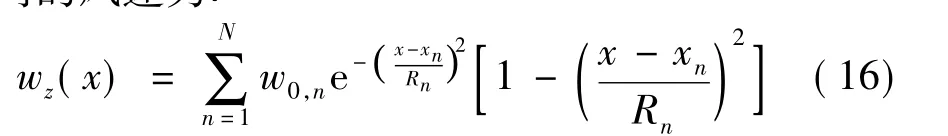
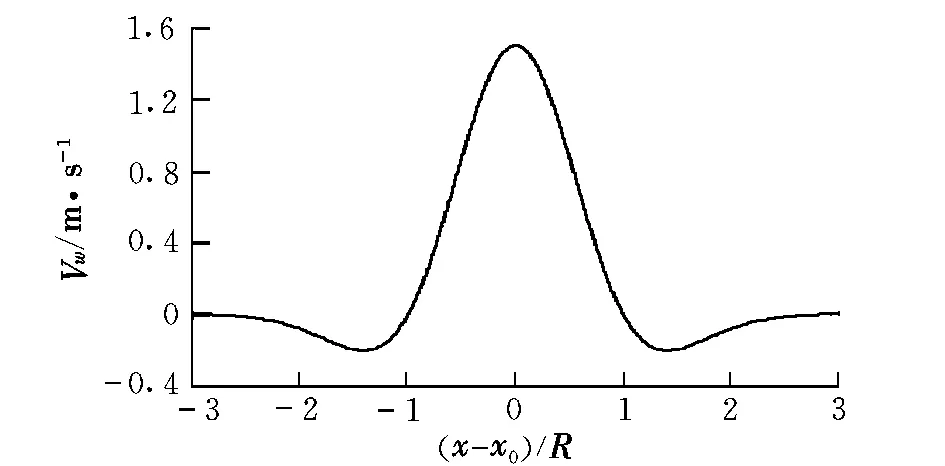
图3 上升热气流风场模型Fig．3 The thermal wind field model

5.2 仿真分析验证

在上节介绍的上升热气流中进行仿真验证分析，风场特性如图4所示，飞行距离为4 000m，仿真结果如图5、图6所示。从图中可以看出，相对于以最大升阻比状态飞行，采用本文的方法在能量消耗上更少，并且俯仰角、迎角和空速均在所允许的范围内。可见小型无人机可以通过采用本文方法从大气扰动中获取能量，以达到减少能量消耗的目的。

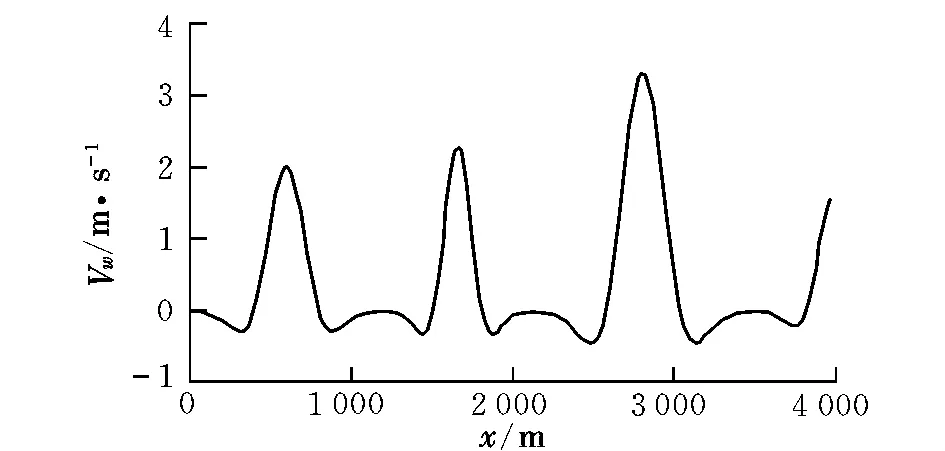
图4 仿真风场特性Fig．4 The characteristics of the simulation wind field

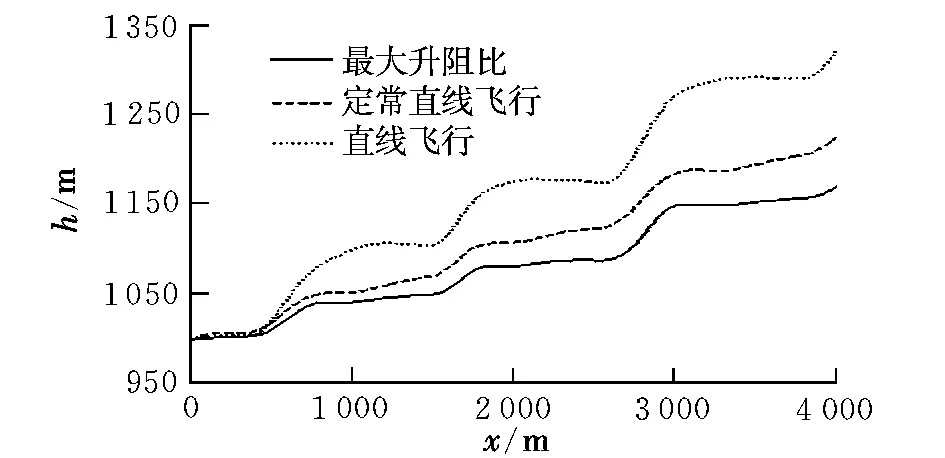
图5 仿真结果Fig．5 Result of simulation

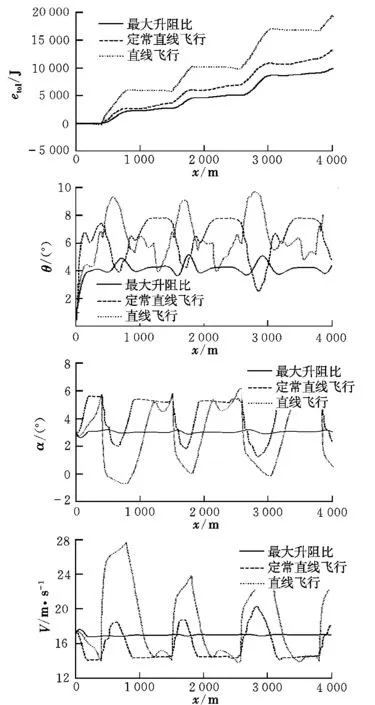
图6 仿真结果Fig．6 Result of simulation

6 结束语

本文针对小型无人机在大气扰动中飞行的能量获取问题展开研究，建立相应的数学模型，把能量获取问题转化为轨迹优化问题，构造优化模型进行求解，并进行控制律的设计，最终通过仿真分析表明小型无人机可以对大气扰动中的能量加以利用，以达到增加航程航时的目的。本文只考虑了纵向问题，同时只在上升热气流中进行了仿真验证，下一步将在更加复杂的风场中进行仿真分析，并综合考虑横向问题。

［1］Langelaan JW，Bramesfeld G．Gust energy extraction for mini-and micro-uninhabited aerial vehicles［R］．AIAA-2008-0223，2008．

［2］Depenbusch N T，Langelaan JW．Receding horizon control for atmospheric energy harvesting by small UAVs［R］．AIAA-2010-8177，2010．

［3］Anjan Chakrabarty，Langelaan JW．Flight path planning for UAV atomosheric energy harvesting using jeuristic search［R］．AIAA-2010-8033，2010．

［4］吴森堂，费玉华．飞行控制系统［M］．北京:北京航空航天大学出版社，2005．

［5］Gedeon J．Dynamic analysis of dolphin style thermal cross country flight［J］．Technical Soaring，1973，3(1):9-19．