ELCIRC源程序代码分析

杨 飞，杨文俊，杨 森

（1.长江科学院水利部江湖治理与防洪重点实验室，武汉 430010；2.重庆市武隆县水务局，重庆 408500）

ELCIRC源程序代码分析

杨 飞1，杨文俊1，杨 森2

（1.长江科学院水利部江湖治理与防洪重点实验室，武汉 430010；2.重庆市武隆县水务局，重庆 408500）

开放源程序代码ELCIRC是采用基于水平向无结构网格、垂向z坐标体系和半隐格式的欧拉－拉格朗日有限体积／有限差分方法来解浅水方程。研究了ELCIRC中除控制方程组求解以外的部分，分析了源程序在插值计算、拓扑结构、定解条件、分层信息和干湿法等技术上的具体操作，尤其是对欧拉拉格朗日模型特有的逆向追踪算法做了详细阐述。同时讨论了一些细节问题，在不恰当的地方给出一些参考和建议，避免小数做分母、相近数相减引起的较大误差。然而，这些经过实际应用的算法原理，可以为我们开发水动力学模型提供有价值的参考。

ELCIRC；逆向追踪；源代码；三维水动力学模型；算法

1 研究背景

ELCIRC［1］模型（Eulerian-Lagrangian CIRCulation）是美国俄勒冈健康与科学大学海岸陆地边缘陆缘研究中心（Oregon Health＆Science University OHSU’s Center for Coastal and Land-Margin Research）基于对哥伦比亚河的研究，开发的哥伦比亚环流模型CORIE的一部分，可以单独用于模拟计算。模型已进行基准测试，并应用到哥伦比亚河的物理过程的模拟。国内外应用逐渐增加，Myers和Aikman2003年研究St.Johns河流域洪泛区淹没过程［2］。杨金艳等2006年利用ELCIRC计算了长江口的潮流场［3］，该模型的中文介绍可以参考杨金艳［3］硕士毕业论文。Gong等2008年将ELCIRC应用到海南新村泻湖研究中［4］，Gong等2009年使用ELCIRC检验了Chesapeake海湾水位对选定的3组东北风响应及正压模式下潮下带海湾河口水交换［5］。Dias等2009年利用水动力ELCIRC和输移VELA，VELApart模型在葡萄牙福尔摩挲河口泻湖的应用，研究入口位置改变的影响［6］。Picado等2010年以葡萄牙阿威罗泻湖为例研究了局部地形调整对潮汐可能产生的影响，采用ELCIRC模型研究在过水面积增加、泻湖的水动力条件减弱下可能的潮汐变化［7］。

ELCIRC采用了基于水平向无结构网格、垂向z坐标体系下，半隐格式的欧拉－拉格朗日有限体积／有限差分方法来解浅水方程。算法上考虑了多种紊流闭合模式，也包括了潮汐势，大气压梯度项及水气交换，可以模拟多种物理过程［1］。图1为以3D斜压哥伦比亚河环流模拟为例的ELCIRC求解过程结构图，网格水平节点33 634个，水平单元50 389个，垂向分层62个，对应总的活动柱面约为2.2×1012个［1］。本文主要涉及的是动量方程组求解以外的参数处理等，文中大部分程序语言来自文献［8］中的ELCIRC5＿4c。

2 拓扑关系

程序首先使用平面的单元、边、顶点来表示实际区域，然后进行垂向划分。实际的计算三维网格为柱体，实际中用到的变量定义位置如图2。字母t和s（或tem和sal）表示温度和盐度，q2和xl表示紊流模型中的紊动能和混合长，字母p（或nd）表示节点处，字母e（或el）和c表示单元中心，字母s（或sd）表示侧面中心，字母z表示垂向分层，0表示初始，diff表示扩散，tmp表示过程量，half表示相邻垂向分层平均，tot表示垂向累积，rho表示密度，bt表示逆向追踪。对于流速，下标n和t表示法向和切向，下标u，v和w表示节点处流速，后面的数字1和2对应迭代计算过程不同时段。图中d表示厚度，但程序中多数变量会将d作为首字母，表示双精度数值，将n作为首字母表示整数值，如单元、节点和边的序号。

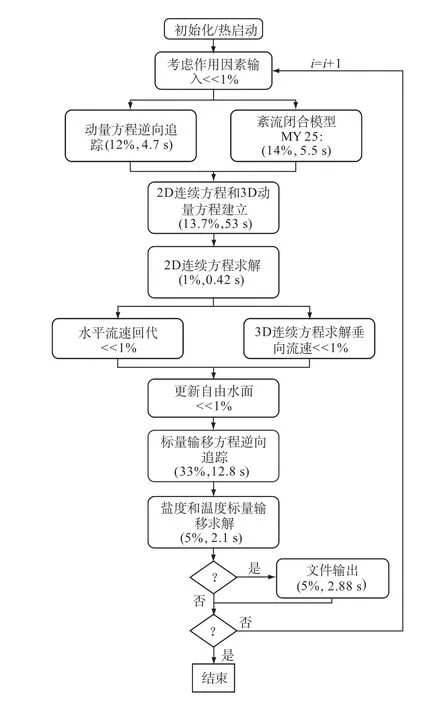
图1 ELCIRC计算流程图［1］Fig.1 Flow chart of ELCIRC［1］

图2 程序常用变量定义位置Fig.2 Position of program variables in grid

2.1 平面位置关系数组

nx（4，4，3），考虑三角形和四边形2种单元，见式

（1）。数组实现循环三角形1－2－3循环和四边形的

1－2－3－4循环。注意，在平面网格生成文件hgrid.in中，单元对应的节点就是按照空间位置逆时针的顺序表述，数组可以循环寻址，起点任意。实际中调用非零元素来得出边与节点在单元中的相对位置关系。

2.2 边正向判定

离散网格的每条边其实是矢量，有（正）方向，端点定义为起止节点，边的正向和单元编号关系紧密。一般情况下单元编号是按照空间位置由下到上、由左到右顺序编排的，这给边的定义带来极大的方便。对于内部边，对应2个相邻单元，边的法线方向为由编号低的垂直边指向编号高的；对于组成区域边界的边，其只对应一个单元，即边界单元，边的法线方向为由单元内部垂直边指向外。边的切向均为法线方向逆时针旋转90度。假定边为j，存储时采用x轴正向到边夹角的正弦值snx（j），余弦值sny（j），边的法向单位向量表示为（snx（j），sny（j）），切向单位向量为（－sny（j），snx（j））。

在计算单元i的水位时，其中j边的法向正负符号Ssign（i，j）表达式具体为

3 逆向追踪

逆向追踪从边的中点（侧面中心x0，y0，z0）出发，根据该点t时刻的速度，显式倒推判断Δt以前该质点位置（xt，yt，zt）。网格无水和流速小于10－6m／s，不需要逆向追踪计算，垂向流速为侧面四顶点垂向流速平均值。由于方程建立在边上，每条边都要考虑逆向追踪方程，上面是依据边来搜寻逆向追踪的需要网格，边界以外的边都对应2个单元，一般优先考虑编号小的单元。

3.1 定位（quick-search）

（x0，y0）在nel单元内，倒推得到的（xt，yt）也在nel内时，确定zt所在层jlev即可，但不能溢出边界；（xt，yt）不在nel内时，找出nel与（x0，y0）、（xt，yt）连线（这时（x0，y0）可以先微调内移，使其不在边上）相交的一边及交点（用到下面的intersect2函数），求出交点的高程，并用交点代替（x0，y0）作为起点，共用该边的单元作为新的nel单元，继续迭代直到（x0，y0）、（xt，yt）在同一单元内。（x0，y0）的速度值是取所属边速度（两端点速度均值，求解动量方程不考虑时间因素，流场过程知道时求解物质输移方程时要考虑速度随时间变化），这样简化默认相邻节点间的速度差异在误差允许范围内。笔者认为可以根据端点线性插值交点速度，保证一阶精度。每次确定新起点后，（xt，yt）根据剩余时间和起点速度重新确立。整个过程如图3所示，该图时间步长dtb不同于文献1中图4所示整个时间步长dt。从t到t－dtb的迭代次数不能预先知道，因此要限定以避免进入死循环。

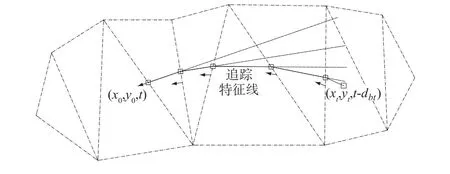
图3 一次逆向追踪迭代示意图Fig.3 Back-track iteration for one sub step

整个过程中并没有考虑z向速度的逆向追踪，这与动量积分方程建立在水平法向和切向是一致的。逆向追踪遇到边界时，只取切向速度。时间步长Δt划分越小，误差就越小，因此把原来的时间步长在计算有效性（整个程序的计算时间长短和计算量的大小）前提下适当细分ndelt个子步长dtb，进行迭代ndelt次逆向追踪迭代（dtb＝Δt／ndelt），每次迭代得到的（xt，yt）作为下次的起点。

3.2 交叉点（intersect2）

判断端点为（x1，y1）、（x2，y2）和（x3，y3）、（x4，y4）两线段有无交点，若有交点，则存在0－1之间的2个数tt1，tt2，满足：

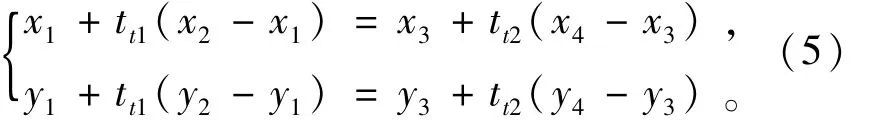
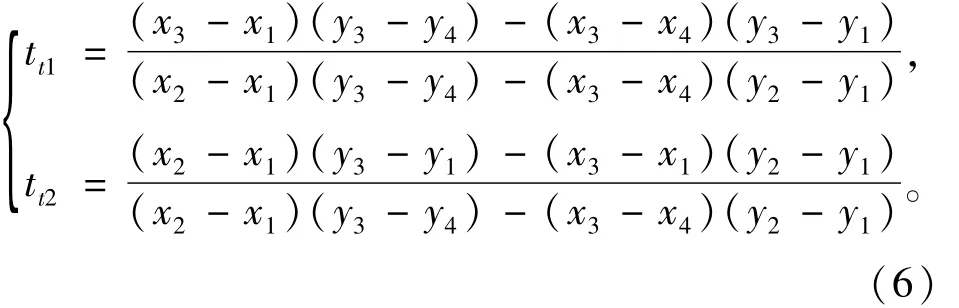
判断tt1，tt2是否在0和1之间，即可确定有无交点，若有，则可求出交点。

3.3 逆向追踪（back-track）

利用quick-search函数找到（x0，y0）对应的（xt，yt）以及nel后，确定（xt，yt）所在的平面，垂向插值nel单元在该平面顶点值，然后根据在单元的相对位置，平面插值（xt，yt）。

单元为三角形时，（xt，yt）与顶点连线将其分为3个小三角形，（xt，yt）的值为3顶点值的加权平均，权重为顶点所对应的小三角形与单元面积之比。单元为四边形时，需要双线性投影变换，中心对应新的坐标原点，原来的点1，2，3，4或点A，B，C，D映射坐标为（－1，－1），（1，－1），（1，1），（－1，1），如图4。分别讨论平行四边形、梯形、不规则四边形，任意一点P的投影变换后的坐标（ξ，η）。

图4 四边形单元双线性投影Fig.4 Bilinear projection of quadrilateral unit

平行四边形时，如图5（a）所示。

式中：X，E分别是2条边的中点，O为平行四边形的中心，（xt，yt）即为P点。

梯形时，以其中一组对边AB和DC平行为例，另一种情况一样。对边中点连线将梯形分为4个区域。如图5（b），M，N为对角线BD和AC的中点，E，F，G，H为AB，BC，CD，DA的中点，O为HF和EG的交点。SP平行底边，延长线交BC于I，ξ大小为SP／SI，η大小为OS／OG。

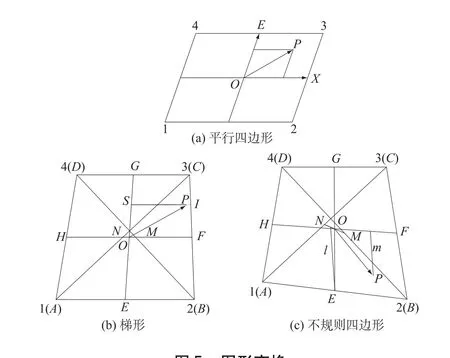
图5 图形变换Fig.5 Graphic transformation

一般对不规则四边形，如图5（c）所示，其算法为

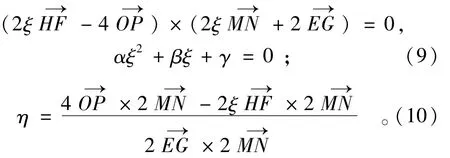
式中：α＝2 H→F×2M→N；β＝2 H→F×2→EG－4 O→P×2 M→N；γ＝－4 O→P×2→EG。求解一元二次方程式（9）得到ξ的2个根，选择绝对值小于1的根，代入式（10）中求解η。

3.4 算法误差

程序原有的计算不规则四边形（图5（c））使用到向量M→N和→AD×C→B（记为d）。数值计算要求数

eta值稳定，在设计算法时还应尽量避免误差危害，防止有效数字损失，要避免两相近数相减和用绝对值很小的数做除数，还要注意运算次序和减少运算次数。在程序判断语句中使用了M→N的分量数值和d是否

eta大于小量small3＝10－5作为判断依据，对于动量方程求解器计算精度为7位有效数字的程序来说，继续将其作为计算乘数和除数，笔者认为会带来不可忽略的误差。考虑到在网格剖分基本优化为正交网格，将会有更多的单元格处在临界条件附近，尽管采用双倍字长计算，相近数相减仍会带来有效位数的减少。因此需要对算法进行修改。

先利用式（7）求出近似值ξ0，令ξ＝ξ0＋Δξ，Δξ是一个未知校正量，然后将ξ0＋Δξ代入式（9）得到式（11），参照式（9）表示成式（12）。

这样由（13）或迭代计算式（14）求解会使得计算的精度有所改善。对求得的小量Δξ加以判断，Δξ太大（如大于0.1）则不采用。

2

2

2

程序中包含判断ξ＞1.1，η＞2.0是否成立的语句，显示出了求解结果的误差，当然，由于速度梯度不大，这种求解误差给结果带来的影响不是很明显，但是较大的计算量和不可忽略的误差确实暴露出这种插值方法的缺陷，现实中存在一些较为成熟的插值算法。为了追求更高的计算精度和求解可靠性，有必要详细根据流体特征分析速度的插值算法。

最后，由所得的ξ，η来确定加权系数，进行插值。

对于物质输移的逆向追踪，要将单元细分为4个子区，四边形是采用对边中点连线划分成4个子四边形，三角形则是3条中位线划分成4个子三角形，判断逆向追踪后质点所属子区，在子区内部进行插值计算（图6、图7）。图6，图7中areas（1），areas（2），areas（3），areas（4）表示所在子三角形面积，作为插值计算的权重。

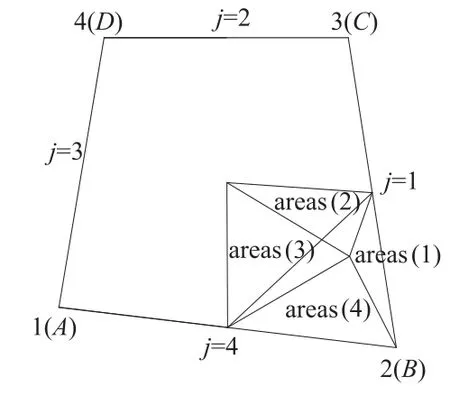
图6 物质输移的四边形插值Fig.6 Interpolation on quadrilateral unit for transport equation

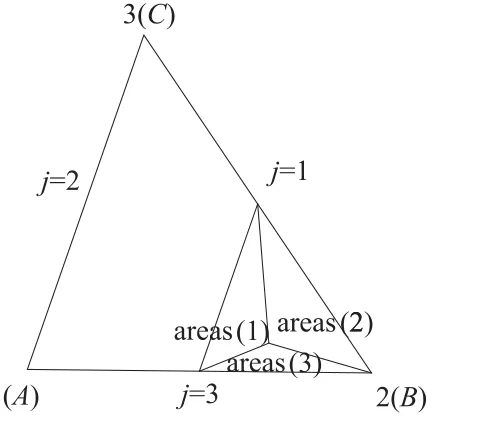
图7 物质输移的三角形插值Fig.7 Interpolation on triangle unit for transport equation

4 定解条件

初始场分布条件是在节点处给定的，温度和盐度都要进行边、单元初始化赋值。陆地边界和开边界在计算中有很大的差别，陆地边界实际限定了流场的范围，干湿判别标准是根据水深是否大于某一临界值确定。在高出水面的陆地区域，也要参与网格剖分，所有剖分的网格都会参与计算；垂向网格剖分时，水体以下部分的柱体也参与计算，相同水平位置的无水柱体，均赋予同一水平位置上最底部有水单元的值，这样处理是为了网格整齐，方便调用求解。

对于水位，一般会有全区域的单一初始值，在计算过程中会逐渐调整为合理值。恒定水流求解问题水流只需给出流量的上边界（进口）条件和水位的下边界（出口）条件，盐度和温度场则根据需要给出进口处的变化过程，非恒定水流求解问题要给出流量的上边界过程和水位的下边界过程。要将给出的进口处流量转化为流速，只是简单的利用开边界宽度来除流量，得到单宽流量，再除以边界水深，因此研究区域和进口边界有相当距离，避免失真流速的影响。

5 网格前处理

在预先分层的网格上确定实际水体的顶底层（源程序标注中M表示顶层号，m表示底层号），初始化单元、节点、边的分层信息。每次迭代求解出水位值后，都要重新计算单元、节点、边的分层信息。以单元为例进行说明，实际水深小于某一特定值时，单元为无水单元，顶层号kfe＝0；否则计算单元新的底层号kbe，顶层号kfe，各层厚度dc和上下邻层平均厚度dchalf。如图8，ztot指的是层面的垂直坐标，nvrt个层对应nvrt＋1个层面，jlev表示层号。逆向追踪中用到的zt表示某质点的实际高度，zup指该点到所在层层顶的距离。顶底同层时，dc＝dchalf＝水深；不同层时顶底层厚dc和dchalf，如图9所示。

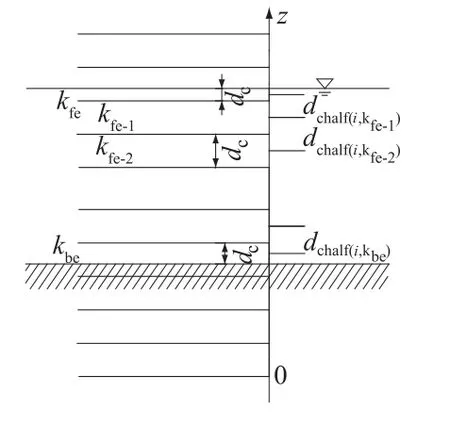
图9 顶底层示意图Fig.9 Schem atic diagram of top and bottom elements

图8 垂向分层示意图Fig.8 Schematic diagram of verticalmeshes

dzhalf，dz要在动量方程做分母（dzhalf（i，kbs－1）、dzhalf（i，kfs）不做分母，kbs，kfs表示边的底层号和顶层号），所以要检查两者是否小于某限定值denom（略小于判定网格干湿时的临界水深），初始水位线应尽量靠近分层的中上部，作为简化，程序中的初始水位设定要求水位线不能靠近层面线。迭代过程中，这种检查只针对顶底同层。ug，vg表示j边上的第k层面上的流速可通过式（15）、（16）线性插值得到

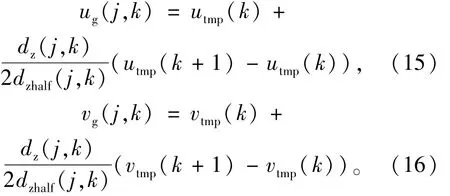
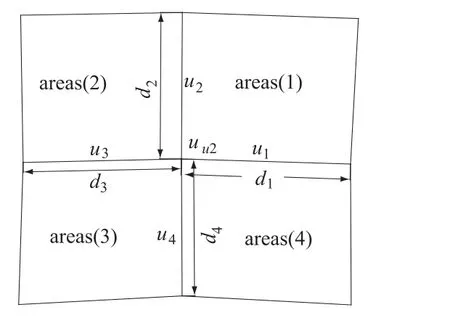
图10 四边形单元节点插值Fig.10 Interpolation w ith nodes on quadrilateral unit

其中utmp（k），vtmp（k）在柱体第k层侧面（平面网格中仍对应j边）面心上的横向和纵向流速。

如图10所示根据距离倒数加权平均求得4条边nd1，nd2，nd3，nd4的公共节点i的x方向流速uu2（i，k）为

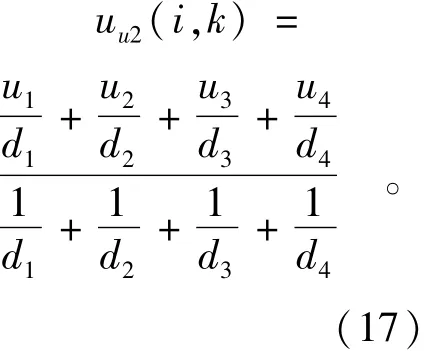
式中u1，u2，u3，u4和d1，d2，d3，d4分别对应nd1，nd2，nd3，nd4四边中点x方向流速和四边长度。Y方向流速vv2（i，k）为

v

g（nd1，k），vg（nd2，k），vg（nd3，k），vg（nd4，k）分别对应nd1，nd2，nd3，nd4四边中点y方向流速，distj（nd1），distj（nd2），distj（nd3），distj（nd4），即式（17）中的d1，d2，d3，d4，表示所在边的长度。节点垂向流速ww2（i，k）则是按周围4个单元垂向流速面积加权平均求得。

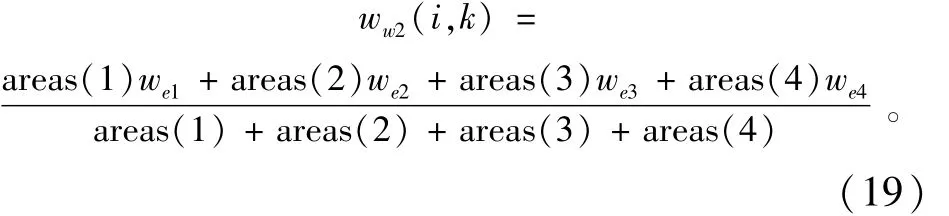
其中areas（1），areas（2），areas（3），areas（4）为4单元面积，we1，we2，we3，we4为4单元垂向流速。节点垂向流速则是按周围4个单元垂向流速面积加权平均求得。

6 结 语

ELCIRC作为水动力学开放源代码，在河口海岸数值模拟中取得一定的成功。文中给出了部分源代码的具体分析，可以为水动力学模型开发人员提供方法实现的参考。源代码凝结了美国俄勒冈健康与科学大学海岸陆地边缘陆缘研究中心科研人员的辛勤劳动，在此表示感谢，笔者只是对其优秀的程序进行部分粗略的学习，重点着眼于其核心部分的欧拉拉格朗日模型逆向追踪过程，发现了其中的不完善的地方，希望能给源程序在改进过程中尽一点努力。ELCIRC的开发人员已经在此代码的基础上进行改进，开发出SELFE程序，本文的大部分都可以为读者学习SELFE提供帮助。

致谢：非常感谢清华大学研究生李健在ELCIRC源代码学习上给予悉心指导和莫大的帮助！

［1］ ZHANG Y L，BAPTISTA A M，MYERSE P.A Crossscale Model for 3D Baroclinic Circulation in Estuary-Plume-Shelf Systems：I.Formulation and Skill Assessment［J］.Continental Shelf Research，2004，24（18）：2174－2214.

［2］ MYERSE P，AIKMAN F，ZHANG A J.A Forecast Circulation Model of the St.Johns River，Florida［C］∥Proceedings of the Eighth International Conference on Estuarine and Coastal Modeling，November 3－5，2003， Monterey，California，USA：144－156.

［3］ 杨金艳.ELCIRC模型在长江口的应用［D］.南京：河海大学，2006.（YANG Jin-yan.Application of ELCRIC Model in Changjiang Estuary［D］.Nanjing：Hohai University，2006.（in Chinese））

［4］ GONG W P，SHEN J，WANG D R.Mean Water Level Setup／Setdown in the Inlet-Lagoon System Induced by Tidal Action：A Case Study of Xincun Inlet，Hainan Island in China［J］.Acta Oceanologica Sinica，2008，27（5）：63－80

［5］ GONG W P，SHEN J，CHO K H，et al.A Numerical Model Study of Barotropic Subtidal Water Exchange Between Estuary and Subestuaries（Tributaries）in the Chesapeake Bay During Northeaster Events［J］.Ocean Modelling，2009，26：170－189

［6］ DIAS JM，SOUSA M C，BERTIN X，et al.Numerical Modeling of the Impactof the Anc~ao Inlet Relocation（Ria Formosa，Portugal）［J］.Environmental Modelling＆Software，2009，24（6）：711－725.

［7］ PICADO A，DIAS JM，FORTUNATO A B.Tidal Changes in Estuarine Systems Induced by LocalGeomorphologic Modifications［J］.Continental Shelf Research，2010，30（17）：1854－1864.

［8］ OHSU’s Center for Coastal and Land-Margin Research.ELCIRC Description：3D Baroclinic Circulation Model［EB／OL］.（2006－05－01）［2011－05－14］，http：／／www.stccmop.org／CORIE／software／elcirc／r ecent.html

（编辑：刘运飞）

Algorithm of ELCIRC Source Code

YANG Fei1，YANGWen-jun1，YANG Sen2
（1.Key Laboratory of River Regulation and Flood Control of MWR，Yangtze River Scientific Research Institute，Wuhan 430010，China；2.Water Affairs Bureau ofWulong County，Chongqing City，Chongqing 408500，China）

Open-source code ELCIRC（Eulerian-Lagrangian CIRCulation）solves the shallow water equations using a semi-implicit Eulerian-Lagrangian finite volume／finite difference method with horizontally unstructured grids and vertically unstretched z-coordinates.ELCIRC source code aside from the governing equation solution is analyzed in this paper.The operation of interpolation，topological structure，definite condition，hierarchy information，and wetting and dryingmethod are described in detail.Back-track，as the key technology of ELCIRC，is expounded comprehensively.Moreover，some detailed problems are discussed，and a few references and suggestions are given to avoid the errors caused by similar number subtraction and by employing small number as the denominator.ELCIRC has been applied in practice and could serve as a valuable reference for developing hydrodynamic models.

ELCIRC；back-track；source code；3-D hydrodynamic model；algorithm

TV148

A

1001－5485（2013）05－0097－06

2013，30（05）：97－102

10.3969／j.issn.1001－5485.2013.05.021

2012－04－25；

2012－06－13

国家自然科学基金面上项目（51079008）

杨 飞（1985－），男，山东泰安人，硕士研究生，从事水力学及河流动力学研究，（电话）13810609717（电子信箱）yangfeihaoyun＠163.com。