水泥型人工髋关节置换治疗老年EvansⅠ-Ⅲ型粗隆间骨折股骨假体的生物力学特性
2013-08-09刘文广刘胜厚殷庆丰肖士鹏王韶进
刘文广,刘胜厚,殷庆丰,肖士鹏,王韶进
山东大学第二医院骨外科,济南 250033
水泥型人工髋关节置换是治疗老年人粗隆间骨折的一种有效方法。但是这种方法是否符合生物力学要求还需要研究。随着计算机技术发展,三维有限元生物力学分析技术在骨科领域的应用愈来愈多。本研究应用三维有限元技术对EvansⅠ-Ⅲ型粗隆间骨折骨水泥型人工髋关节假体置换的股骨假体进行生物力学分析,评价该手术方式的合理性。
材料和方法
材料 研究所用的设备及软件包括:西门子公司生产的支持DICOM 3.0标准的SOMATOM Balance螺旋CT,Intel酷睿双核电脑、图像处理软件Mimics 8.1(Materialise,比利时)、大型CAD/CAM/CAE建模软件Unigraphics(Manitoba,加拿大)及有限元分析软件 ABAQUS 6.5(Dassault Systèmes Simulia Corp,Rhode Island,美国)。
志愿者资料 选择1名75岁健康女性志愿者作为建模素材,身高162 cm,体重70 kg。该志愿者既往身体健康,无髋部及股骨部损伤史,双侧髋关节及股骨X线片检查未见明显异常。
建立EvansⅠ-Ⅲ型粗隆间骨折三维CAD模型
垂直于志愿者的左侧股骨纵轴自股骨头上方由近端向股骨干远端进行CT扫描,扫描参数为:层厚1.0 mm、层间距0.8 mm、窗宽2000、窗位400,共获得248张断层扫描影像,长度448 mm。将DCM格式的图像数据传入PC机,用Mimics软件对图像进行预处理后,输出股骨的IGES格式数据文件。最后将数据导入CAD/CAM/CAE一体化软件 Unigraphics,完成实体仿真模型建立。在股骨三维模型上,以大粗隆尖到小粗隆下缘作为骨折线,移除骨折线以上部分,建立粗隆间骨折三维CAD模型。
建立不同长度人工髋关节股骨假体三维模型及骨水泥三维CAD模型 根据北京爱康公司提供的假体参数 (短柄假体,型号3#,柄长120 mm;长柄假体,型号4#,柄长170 mm),用Unigraphics软件中插入选项中的成形特征,分别形成假体的股骨颈、股骨柄等部分,并通过布尔运算合并各部分,建立假体模型。
建立EvansⅠ-Ⅲ型粗隆间骨折人工髋关节置换三维模型 模拟假体置换过程,将两种不同柄长的股骨假体分别插入粗隆间骨折模型,根据临床经验,为减少假体松动,在假体与股骨间设定厚度为3 mm的骨水泥套层,其长度长于假体远端10 mm。其中小粗隆上1 cm股骨颈截骨线与粗隆间骨折线之间的骨缺损采用5 mm的骨水泥套层填充。
建立三维有限元模型 在ABAQUS 6.5软件中,采用修正的二次四面体单元C3D10M对股骨、假体、骨水泥套层三维模型进行网格划分,建立三维有限元模型。对于关键部位,如假体-骨水泥、骨水泥-股骨接触面,进行网格细化,并打磨锐利边缘,提高分析结果准确性。
材料特性定义 按照国外有限元分析文献报道的参数设定模型材料特性[1]。其中钴铬钼合金弹性模量为2.2×105N/mm2,泊松比为0.3;骨水泥弹性模量2.62×103N/mm2,泊松比0.35;松质骨弹性模量2.13×103N/mm2,泊松比0.3。皮质骨的杨氏弹性模量E1=E2=1.15×104N/mm2,E3=1.7×104N/mm2;剪切弹性模量G1=3.6×103N/mm2,G2=G3=3.3 ×103N/mm2;泊松比 ν1=0.51,ν2= ν3=0.31。
施加边界条件 假定手术后初期假体-骨水泥、骨水泥-股骨接触面稳固,无相对滑动。在股骨远端平面施加边界条件,完全固定股骨,加载垂直载荷,模拟70 kg体重者单腿站立时假体-骨水泥-股骨的应力分布情况。
生物力学分析 用ABAQUS 6.5软件进行三维有限元分析,得出假体置换后股骨假体应力分布情况,并绘制等效应力云图及等效应力曲线。应力为区域内5个位点应力的均值。
结 果
如图1,2显示:长柄股骨假体与短柄股骨假体的应力分布基本相同。
假体颈部有两个应力集中区,分别为假体颈的上部和中下部,接近与假体柄连接处,其中,中下部与小转子上方的交界处应力明显集中。短柄假体颈的上下两个应力集中区的最大应力值分别为 (169.9±0.31)N/mm2和 (207.5±0.28)N/mm2;长柄假体颈的上下两个应力集中区的最大应力值分别为(191.5±0.12)N/mm2和 (227.4±0.35)N/mm2。
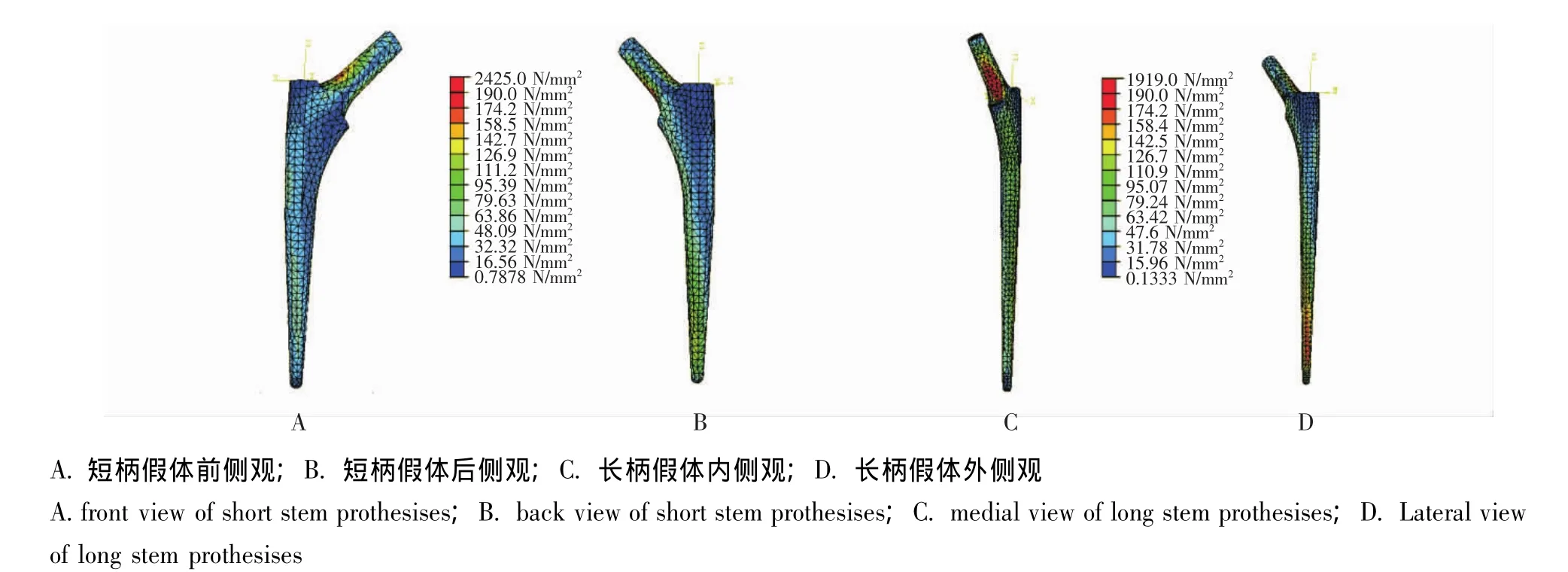
图1 水泥型人工髋关节假体置换后股骨假体的等效应力分布云图Fig 1 Equivalent stress distribution cloud chart after cemented femoral prosthesis implanted
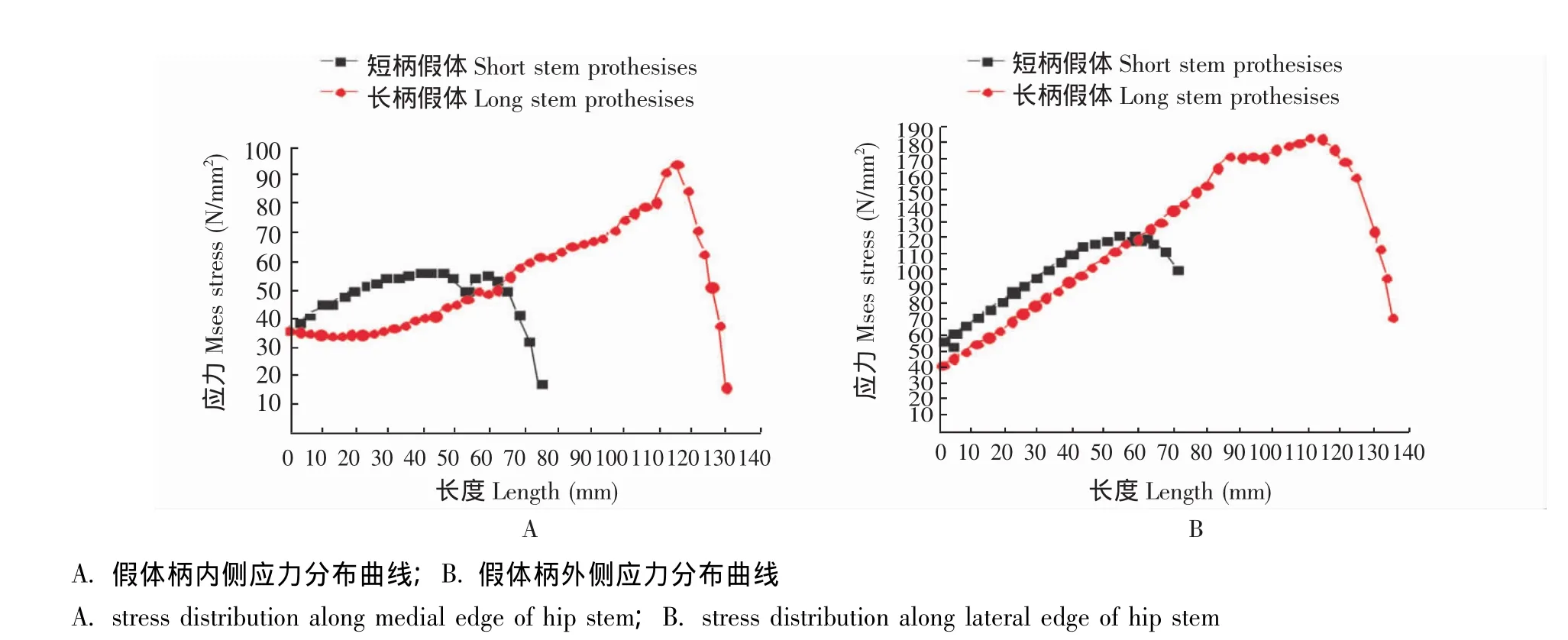
图2 水泥型人工髋关节假体置换后股骨假体的等效应力分布曲线Fig 2 Equivalent stress distribution line chart after cemented femoral prosthesis implanted
假体柄部内侧的颈干交界处相当于股骨矩区域有一较小的应力集中区域,由此向下应力略降低,随之逐渐增大,在接近假体柄内侧末端时形成第2个应力集中区域。假体柄外侧由近端向远端应力逐渐增大,在接近假体末端时形成应力集中区。短柄假体颈柄交界处、内侧末端及外侧末端对应的最大应力值分别为 (85.91±0.33)、(56.11±0.24)和 (121.83±0.19)N/mm2,长柄假体3个应力集中区的峰值分别为 (108.52±0.26)、(94.13±0.13)和 (182.43±0.43)N/mm2。
讨 论
采用三维有限元模型的生物力学研究所得数据的准确度与模型与实际操作的相似度、数据采集的准确性、划分单元格的多少等密切相关。首先模型与临床操作的符合程度对三维有限元分析的准确性具有重要影响。在临床手术时,虽然小粗隆上1 cm股骨颈截骨线与粗隆间骨折线之间的骨质要捆扎回原位,但是由于骨折线的存在,在该部位大部分应力传导中断,因此,骨折愈合前这部分骨质基本不参与应力传导。为了增加该部位抵抗应力的能力,手术时需增加该区域骨水泥的厚度。本研究建立的三维有限元模型最大程度地模拟了实际的手术操作。其次,本研究应用DICOM医学数字图像通讯格式,将CT数据直接传送至计算机,采用Mimics软件建模,减少了数据传输的中间环节,保证了建模数据传输的准确性。最后,网格的划分、单元的大小、形状、数目等均影响模型的精确性[1]。单元的个数越多,网格越密,模型的质量就越高,计算也就越复杂,所得结果也越接近真实值。本研究采用软件程序自动划分网格,短柄假体模型单元数为60548,长柄假体模型单元数为65686,为文献[2-3]报道单元数的6倍。因此,本研究所建立的粗隆间骨折模型具有较高的合理性和实用性。
随着假体制造工艺的提高,假体断裂的机会并不高,但是随着使用年限的延长,特别是在假体松动、骨溶解等病理状态下,假体疲劳断裂的可能性增加;同时假体断裂增加了翻修手术的难度[4-6]。因此,研究假体的应力分布,为假体制造提供依据,可以防止假体断裂。本研究结果显示:在粗隆间骨折行人工髋关节假体置换后,股骨假体的应力分布与常规人工髋关节置换时基本相同,应力集中区分布于假体颈柄交界区域和假体柄部近末端区域[7],应力均未超过钴铬钼合金的断裂应力极值,所以从应力分布方面看,粗隆间骨折行人工髋关节假体置换后股骨假体符合生物力学要求。长柄假体颈柄交界处的应力峰值较短柄假体略高;在柄部的应力集中区域,长柄假体的应力峰值均较短柄假体高30%,尤其在假体柄部内侧近远端区域,前者的应力峰值较后者高67.8%,这可能与长柄假体增加了假体内外翻趋势的力臂有关。长柄假体需要承受更大的应力载荷,特别是在应力集中区域,所以在制造假体时,需在这些区域增加假体的抗疲劳强度,以防止假体的疲劳断裂。
总之,水泥型人工髋关节置换治疗老年EvansⅠ-Ⅲ型粗隆间骨折,股骨假体的应力分布与常规人工全髋关节置换后股骨假体的应力分布相似;长柄股骨假体的各应力集中峰值较短柄股骨假体高,但均没有超过金属断裂的应力极值。
[1]李永奖,张力成,杨国敬,等.人工髋关节假体三维有限元模型构建及其生物力学意义[J].中国骨与关节损伤杂志,2007,22(9):711-713.
[2]尚鹏,王建平,王成焘.完整步态下人工髋关节微动的非线性有限元分析[J].上海交通大学学报,2008,42(4):607-611.
[3]Kayabasi O,Ekici B.The effects of static,dynamic and fatigue behavior on three-dimensional shape optimization of hip prosthesis by finite element method [J].Mater Design,2007,28(8):2269-2277.
[4]Panagiotopoulos EC,Kallivokas AG,Koulioumpas I,et al.Early failure of a zirconia femoral head prosthesis:fracture or fatigue[J].Clin Biomech(Bristol,Avon),2007,22(7):856-860.
[5]Drobniewski M,Sibiński M,Plebański R,et al.Breakage of the prosthesis steam as a rare complication of total hip replacement[J].Chir Narzadow Ruchu Ortop Pol,2010,75(1):53-56.
[6]Lemaire R.Fatigue fracture of the femoral component in a mobile bearing knee prosthesis[J].Acta Orthop Belg,2010,76(2):274-281.
[7]Harrigan TP,Harris WH.A three-dimensional non-linear finite element study of the effect of cement-prosthesis debonding in cemented femoral total hip components[J].J Biomech,1991,24(11):1047-1058.
