基于高光谱的河套灌区农田表层土壤质地反演研究

白燕英，魏占民＊，刘全明，郭桂莲，刘霞

（1.内蒙古农业大学水利与土木建筑工程学院，内蒙古 呼和浩特 010018；2.内蒙古鄂尔多斯市伊金霍洛旗水保局，内蒙古 伊金霍洛旗 017200）

0 引言

河套灌区是内蒙古自治区重要的粮食生产基地，目前灌区对农田土壤的基础监测工作相对落后。土壤质地作为较稳定的土壤自然属性，对土壤结构、孔隙状况、保水性、保肥性、耕性等影响较大。长期以来，土壤质地主要依赖于土壤物理分析方法，要获取区域尺度的土壤质地分布，需要进行大量的采样和分析，速度慢，效率低［1］。遥感技术能提供宏观、实时的连续动态地面观测，决定了它能在灌区尺度上对土壤的基础信息采集发挥重要作用［2］。

对土壤光谱特性的研究是应用遥感对土壤进行监测的基础。土壤是由矿物质、有机质、水和空气组成的三相物质，因此其光谱特性是多种物质光谱的综合表现，普遍认为土壤有机质含量、含水量、氧化铁含量、机械组成、母质等是影响土壤光谱特性的主要理化性状［3］。目前土壤有机质含量、含水量的光谱研究成果较多，而对土壤质地的光谱特性研究相对较少。黄明祥等研究表明，海涂土壤在近红外700～1 200nm之间沙砾含量与光谱反射率的相关性最高，呈负相关且其相关系数达到－0.78［4］。王德彩等建立了精度较高的土壤砂粒、粉粒、粘粒含量的VNIR光谱预测模型［1］。李春蕾等研究表明，野外光谱430nm为土壤砂粒含量的敏感波段，原始光谱对数的倒数与土壤砂粒含量的相关系数在430 nm 处达到最大值0.76［5］。

本文以河套灌区解放闸灌域为研究区域，研究农田表层土壤粘粒、粉粒和砂粒的光谱特性，以建立不同粒径含量与光谱的关系模型，为应用高光谱遥感监测该区域农田表层土壤质地提供理论依据。

1 研究区概况与土壤样品的采集

河套灌区解放闸灌域南北长约87km，东西宽约78km，海拔高程为1 032～1 050m，南邻黄河，北靠阴山山脉的狼山。灌域总控制面积21.568万hm2，其中灌溉面积14.21万hm2，包括农田12.199万hm2，林果地0.551 万 hm2，牧草地1.461 万hm2［6］，其中农田面积占总灌溉面积的85.85%。

野外土样采集时间为2012年3月28－31日，此时，土壤表层已经解冻，农作物还没有种植。采样对象为农田表层0～10cm土壤，范围遍布整个灌域，研究区概况及57个采样点位置如图1所示。采样方法：为了与ETM＋遥感图像（分辨率30m×30 m）相对应，尽量选取地面特征一致、长宽均大于50 m的农田，在农田中央采用“X”法取样，计5个点（GPS定位），混合土样，并用相机对采样点实地状况拍照。

2 实验室分析

研究区域土壤矿物质组成基本一致，有机质含量为0.21%～3.08%，平均1.3%，含量较低。有关研究表明，土壤有机质含量大于2.0% 时，其与光谱反射率之间相关性较好，而小于2.0% 时，其它土壤理化性质对光谱的影响将会掩盖土壤有机质对光谱的影响［7］。在常温下自然风干土样以去掉土壤水分对光谱的影响，尽可能减少土壤质地以外因素对土壤光谱的影响。土样风干后，剔除植物残茬、石粒等杂质，磨细，过1mm孔径筛，充分混匀，分成两份，一份用于实验室土壤质地分析，另一份用于土壤光谱测定。

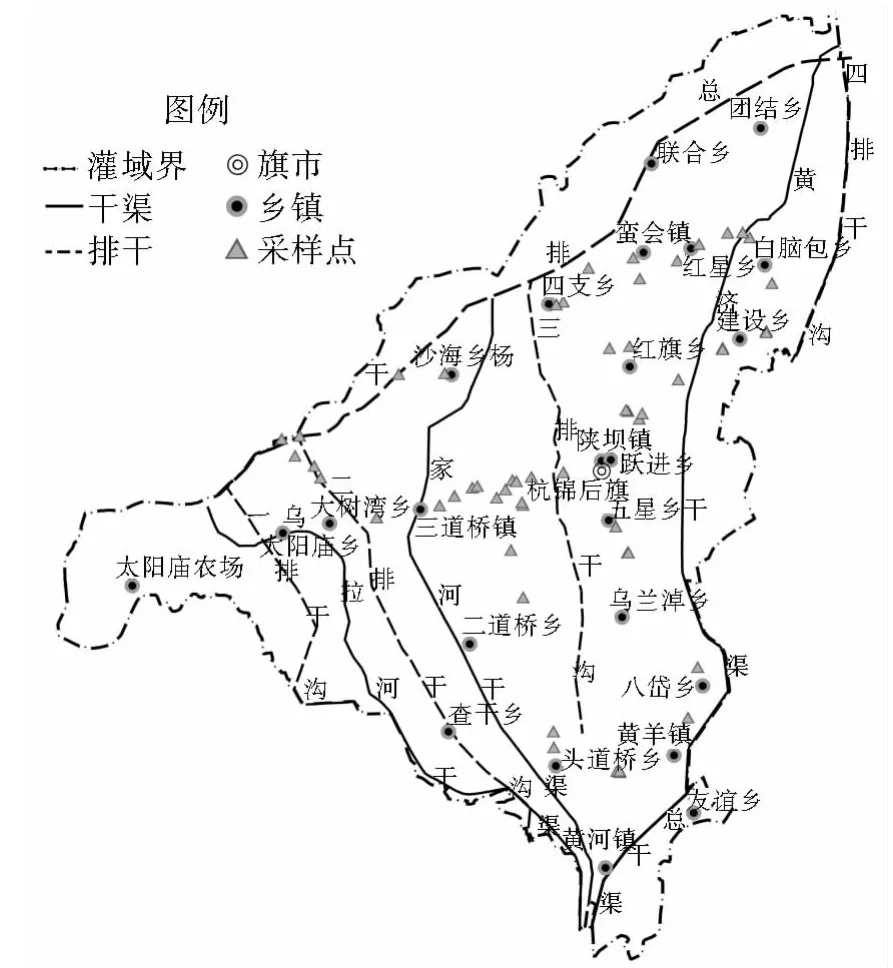
图1 解放闸灌域概况及采样点分布Fig.1 General situation of Jiefangzha irrigation sub－district and distribution of sampling points

2.1 土壤质地测定

采用德国新帕泰克HELOS／BR粒度仪测定土壤质地，土壤粒级划分采用中国制，粘粒为0～2 um，粉粒为2～50um，砂粒为50～1 000um。采样点土壤质地的统计特征见表1。

表1 土壤质地的统计特征值Table 1 Statistical characteristic of soil texture

2.2 土壤光谱测量

实验室光谱测量采用ASD FieldSpec Hand－Held光谱仪，光谱范围325～1 075nm，重采样间隔为1nm。实验在暗室内进行，被测土样装满（与培养皿上缘齐平）直径为10cm、深1cm的玻璃培养皿内（认为是光学上无限厚），将视场角为25°的探头置于土样15cm的垂直上方。另有2台能够提供平行光的50W的卤光灯，光源位于土样两边距土样约50cm、30°的照射角度。每间隔10min重新优化一次光谱仪的积分时间并对参考白板进行反射校正，每次优化和对白板的反射校正进行10次重复，每个土样的反射光谱测量也进行10次重复。光谱两端（325～420nm，900～1 075nm）受暗电流、温度和环境影响较大，存在较大噪声，本次研究去除325～370 nm和1 000～1 075nm波段，对370～420nm和900～1 000nm波段进行去噪处理。本文采用Matlab7.0工具箱基于小波变换的阈值去噪方法，以“sym8”作为小波母函数，选择“Rigorous SURE”为阈值方法、“Scaled white noise”为噪声结构进行去噪和平滑处理。去噪后的光谱进行10nm间隔重采样，得到370～1 000nm范围共64个光谱波段。

3 数据处理

3.1 土壤粒级含量与光谱反射率的相关性分析

分别对57个土样的粘粒、粉粒、砂粒含量与光谱反射率进行相关分析，去掉3个异常点，剩余54个样本，分别得到粘粒、粉粒、砂粒含量与光谱反射率的相关系数（图2）。相关性分析结果表明，粘粒含量与光谱反射率的相关性小于粉粒、砂粒与光谱反射率的相关性。其中粘粒含量与反射率呈正相关，相关系数范围0.407～0.462；粉粒含量与反射率呈正相关，相关系数为0.322～0.657；砂粒含量与反射率呈负相关，相关系数为－0.369～－0.673。其中粘粒含量与各波段的相关性变化趋势不明显，在370 nm处最大；粉粒含量与砂粒含量与各波段的相关性随着波长的增加而增加，在1 000nm处最大。

3.2 土壤粒级含量与光谱反射率各种变换形式的相关性分析

为寻找土壤粘粒、粉粒和砂粒含量的最佳敏感波段和反演方程，本研究选取4种土壤光谱的变换形式，包括反射率倒数1／R、反射率对数log R、反射率倒数的对数log（1／R）、反射率对数的倒数1／log R，及步长10nm、20nm、30nm、40nm、50nm 的反射率差分、1／R 差分、log R 差分、log（1／R）差分和1／log R差分，应用Matlab软件实现光谱的上述变换，分别得到与粘粒、粉粒和砂粒含量相关系数最大的20个波段的变换形式，由于篇幅有限，本文仅列出相关系数最大的前10个波段的变换形式（表2）。

粘粒含量不仅与光谱反射率的差分相关性好，敏感波段集中在550～630nm，还与反射率倒数差分相关性好，敏感波段主要集中在690～750nm，且与710nm、740nm波段的反射率倒数差分相关性最好，决定系数为0.31，明显大于其与原始反射率的最大相关系数0.21；粉粒、砂粒含量仅与光谱反射率差分相关性好，敏感波段集中在440～540nm，且粉粒、砂粒含量与480nm和510nm波段的差分相关性最好，决定系数分别为0.57和0.56，也明显大于其与原始反射率的最大相关系数0.43和0.45。

图2 粘、粉、砂粒含量与，反，射率的相关系数Fig.2 Correlation coefficient of claysiltsand content and reflectance

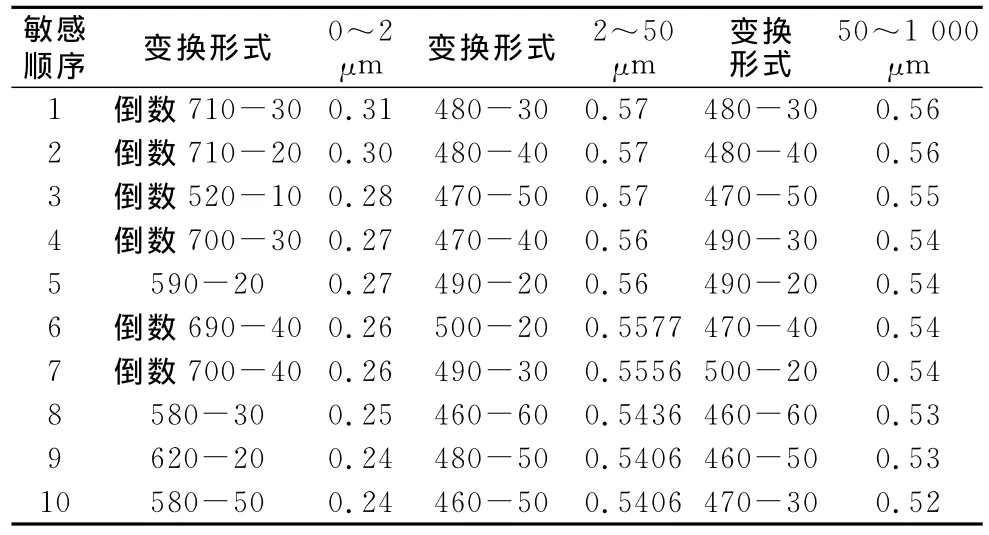
表2 土壤粒级含量相关性最大的10个波段及决定系数Table 2 Ten sensitive bands of clay，silt，sand content and determination coefficient

4 模型建立

上述研究表明，粘粒、粉粒和砂粒都有其对应的敏感光谱波段，敏感程度主要靠不同粒径含量与其对应的波段相关性体现，相关性越大的波段表明越能明显地反映其对应的土壤粒径含量。本文应用一元线性回归模型和BP神将网络模型建立不同粒径含量与其对应的敏感光谱波段关系模型，并比较两种模型的精度。本文总样本数54个，随机选取40个样本（总样本数的3／4）建模，另外14个样本（总样本数的1／4）用于模型精度检验。

4.1 一元线性回归模型

根据表2可知，粘粒含量与710nm和740nm波段的反射率倒数差分相关性最好，粉粒、砂粒含量与480nm和510nm波段的差分相关性最好，本文应用上述波段分别与粘粒、粉粒和砂粒含量（%）建立一元线性回归模型（图3），回归方程为：

式中：X1为740nm与710nm波段反射率的倒数差分1／R740－1／R710；X2、X3均为 510nm 与480nm波段反射率的差分R510－R480；Y粘、Y粉、Y砂分别为粘粒含量（%）、粉粒含量（%）和砂粒含量（%）。

图3 土壤粒级含量与最敏感波段回归模型Fig.3 Regression model of the most sensitive band and clay，silt，sand content

4.2 BP神经网络模型

本研究选取粘粒、粉粒和砂粒BP神经网络模型输入层的节点数为5、10、20，即输入数据分别是与粘粒、粉粒和砂粒含量相关系数最大的前5、10、20个光谱反射率变换形式（表2）。输出层为1个节点，分别对应粘粒、粉粒和砂粒含量，隐含层为1层，其节点数需要根据输入层节点数不同在试验中不断调整，最终确立5－15－1、10－30－1和20－60－1（输入层神经元个数－隐含层神经元个数－输出层神经元个数），即隐含层节点数为输入层节点数的3倍时，BP模型模拟精度最高。网络隐含层传递函数、输出层传递函数均选择tansig函数，训练函数选取traindm（附加动量的梯度下降法）。首先用premnmx函数对样本数据做归一化处理，学习速率为0.01，最大训练次数为1 000，训练完毕后再用postmnmx函数对计算结果反归一化，模型在Matlab7.0下编程实现。

4.3 模型精度检验

用建模以外的14个样本对上述两种模型的精度进行检验（表3），将模型计算值（相对于实测值）的平均计算精度、均方根误差（RMSEP）和决定系数（R2）作为标准来评价模型的优劣，其中RMSEP越小越好，平均计算精度、决定系数越大越好。

表3 模型检验精度比较Table 3 Comparison of model precision

模型检验结果表明两种模型对粘粒、粉粒和砂粒含量的预测精度较高，都在85%以上。其中输入层节点数为20的粘粒、粉粒含量BP模型的预测精度略高于节点数为5的BP模型，但砂粒含量的BP模型预测精度却略低于节点数为5的BP模型，说明BP神经网络模型的输入层节点数对计算结果影响不大。粘粒、粉粒、砂粒BP模型的均方根误差略小于一元回归模型，平均计算精度略高于一元回归模型，粘粒含量的BP模型的决定系数大于回归模型，只有粉粒、砂粒含量的BP模型的决定系数略小于回归模型。总体上两种模型精度基本一致，BP神经网络模型略微优于一元线性回归模型，但BP神经网络模型计算复杂，输入层神经元个数、隐含层神经元个数、传递函数、训练函数的选择等都会影响模型的预测精度，而且计算过程需要不断调试；而一元线性回归模型方法简单，便于操作，预测结果稳定，在两种模型精度基本一致的情况下，可以优先考虑原理及应用都较为简便的一元线性回归模型。

5 结论

研究结果表明，粘粒含量与波段550～630nm的反射率差分和690～750nm反射率倒数差分相关性较好，粉粒、砂粒含量仅与波段440～540nm反射率的差分相关性较好；粉粒、砂粒含量与光谱反射率的相关程度接近，粘粒含量与光谱反射率的相关程度低于粉粒、砂粒含量与光谱的相关程度。

建立了粘粒、粉粒和砂粒含量与其对应的敏感波段的一元线性回归模型和BP神经网络模型，模型检验结果表明，分别针对粘粒、粉粒和砂粒含量建立的两种模型精度都较高（大于85%），并且两种模型的平均计算精度、均方根误差（RMSEP）和决定系数（R2）基本相同，说明该研究成果可以用于河套灌区农田土壤质地反演研究。该研究结果可为下一步应用高光谱遥感图像大范围识别河套灌区的土壤质地提供理论依据。

但在实际应用中，土壤水分是影响土壤光谱的最明显因素之一，土壤光谱反射率在一定的土壤水分临界值之下时，会随着含水率的增加而降低，当超过临界值时，会随着土壤水分的增加而增加［8］。如何考虑土壤存在水分时，应用高光谱反演土壤质地将是下一步研究的内容。

［1］ 王德彩，邬登巍，赵明松，等.平原区土壤质地的反射光谱预测与地统计制图［J］.土壤通报，2012，43（2）：257－262.

［2］ 徐美，李纪人，阮本清.灌区遥感应用［J］.水土保持研究，2006，13（5）：23－26.

［3］ 高永光，胡振琪.高光谱遥感技术在土壤调查中的应用［J］.矿业研究与开发，2006（2）：44－46.

［4］ 黄明祥，程街亮，王珂，等.海涂土壤高光谱特性及其砂粒含量预测研究［J］.土壤学报，2009，46（5）：932－937.

［5］ 李春蕾，许端阳，陈蜀江.基于高光谱遥感的新疆北疆地区土壤砂粒含量反演研究［J］.干旱区地理，2012，35（3）：473－478.

［6］ 陆圣女.基于GIS解放闸灌域土壤墒情变化规律及预报模型研究［D］.内蒙古农业大学，2008.

［7］ 张晋.土壤光谱特性的研究［D］.西北农林科技大学，2008.

［8］ LIU W D，BARET F，GU X F，et al.Relating soil surface moisture to reflectance［J］.Remote Sense.Environ.，2002，81（2／3）：238－246.