斜交简支钢箱梁桥实用计算方法探讨

高 金

（上海勘测设计研究建筑市政分院，上海市 200434）

0 引言

随着城市道路和公路建设的发展，钢桥以其特有的优势，被越来越广泛的应用。与同等跨径的混凝土梁桥相比，钢桥梁高低，可用于解决城市高架桥梁和公路跨线桥的净空不足问题。而且钢桥便于工厂制造、运输，便于无支架施工，工地安装速度快，能够很大程度的减小施工对桥下通行或通航的影响。桥梁的建设受所跨河道走向或桥下原有道路线形的制约，使得斜交桥梁不可避免，箱型截面抗扭刚度大、整体性好，因此斜交钢箱梁桥逐渐成为一种常用的桥梁结构型式，对斜交钢箱梁桥的分析和研究也越来越受到设计人员的重视。

1 斜交梁桥分析方法

斜交梁桥比正交梁桥受力复杂，主要是因为斜桥受力存在弯扭耦合，斜交梁桥的纵向主弯矩比同跨径同宽度的正交梁桥小，并随斜交角的增大而减小，同时钝角区域反力比锐角区域反力大，某些情况下，锐角区域可能出现负反力。

斜交箱梁桥目前常用的计算方法有以下几种：

（1）平面单梁模型法

将空间受力简化为平面受力，不考虑斜桥效应和箱梁扭转，主梁和横梁分别单独计算。该方法仅适用于斜交角度较小且宽跨比较小的箱梁桥，有其自身的局限性。

（2）空间单梁模型法

即鱼骨梁模型，模型由一根纵梁和多个支点横梁构成，将全桥质量（平动质量和转动质量）和刚度（竖向抗弯刚度、横向抗弯刚度、扭转刚度）集中在纵梁上，支点横梁起到横向分配反力的作用。实际工程设计中多用于初步设计和内力估算。

（3）空间梁格模型法

将箱梁桥离散成一个等效梁格，将分散在原结构中每一区段的弯曲刚度和抗扭刚度集中于最邻近的等效梁格内。实际结构的纵向刚度集中于纵向梁格单元上，横向刚度集中于横向梁格单元上。理想刚度的等效原则：当原型实际结构和对应的等效梁格承受相同荷载时，两者的挠曲线是恒等的，并且每一梁格内的弯矩、剪力、扭矩等于该梁格所代表的实际结构内力。梁格法建模过程相对简单，计算的准确性相对于平面单梁模型和空间单梁模型来说要高，输出的梁单元计算结果与规范对应，方便设计人员进行结构验算和配筋，这些优势使得空间梁格模型法成为分析斜弯梁桥和异形梁桥常用的方法。

（4）实体、板单元模型法

实体、板单元模型与实际结构最为接近，能够考虑各种结构的受力问题，包括箱梁翼板的有效宽度、形心位置、箱梁的畸变和翘曲等，但分析模型复杂，建模时间长，输出结果不能直接用于结构的验算和配筋，在实际工程设计中较少采用。

2 工程实例

某桥是一座位于城市支路上跨越内河航道的斜交简支钢箱梁桥，桥梁与河道顺交20°，跨径51 m，横向布置为0.3 m（栏杆）+4.5 m（人行道）+3.5 m（非机动车道）+8 m（机动车道）+3.5 m（非机动车道）+4.5 m（人行道）+0.3 m（栏杆）=24.60 m。景观要求桥梁侧立面需营造拱的效果，因此跨中梁高2.0 m，支点梁高3.1 m，跨中等高段长20 m，支点等高段长1.94 m，中间变高段采用直线过渡。本桥横断面为单箱4室箱形截面，悬臂长2.5 m，腹板间距4.9 m。纵向每3 m左右设置一道横隔板，横隔板在跨中等高段垂直于道路设计线布置，在支点等高段与纵梁斜交70°，其他横隔板在两者之间逐步旋转过渡。全桥采用Q345d钢材。跨中标准横断面见图1，桥型总体布置见图2。

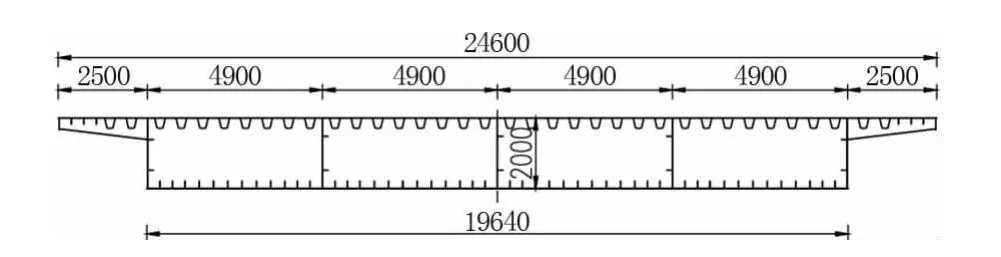
图1 钢箱梁跨中标准横断面（单位：mm）

3 计算分析

3.1 计算模型建立

本桥宽跨比和斜交角均较大（宽跨比接近0.5，斜交角20°），平面单梁模型法显然不适用。考虑使用空间单梁模型法和梁格模型法对该桥进行结构分析，并建立板单元模型验证其结果的准确性。

采用Midas Civil2011建立该桥的空间单梁模型，模型的纵梁截面与一般的平面单梁模型截面相同，需考虑顶底板和腹板的纵向加劲肋对截面特性的影响。注意钢结构箱型截面为薄壁截面，可在CAD中先绘制出钢箱梁的特征截面，线的位置宜画在板厚的中央，然后在Midas Civil2011的spc截面特性计算器中导入CAD文件，赋予顶底板腹板及加劲肋厚度，边腹板和顶底板形成loop。纵梁的有效分布宽度参考英国BS5400规范计算，跨中截面的有效分布宽度系数为0.984，四分点为0.980。支点横梁用工字型截面模拟，工字型的腹板厚度取支点横梁厚度，翼缘长度为相邻横隔板间距的一半，支点横梁与纵梁斜交20°。空间单梁模型及边界条件见图3。

采用Midas Civil2011，将结构离散为纵梁腹板和横隔板组成的梁格模型，模型及边界条件见图4。钢箱梁截面的每根腹板为一根纵梁，通常称为实纵梁，为后期加二期荷载和活载方便，可在悬臂端部设置虚纵梁，本梁格模型只计算结构自重作用，故未设置虚纵梁。实纵梁单元截面为顶底板带加劲肋的工字型截面，翼缘宽度为相邻腹板间距的一半，有效分布宽度与空间单梁模型相同。每片横隔板为一根横梁，横梁单元截面为工字型，在非人孔处工字型的腹板为横隔板的厚度，在有人孔处腹板厚度设为1 mm，翼缘宽度为桥梁设计中心线处相邻横隔板间距的一半，横梁高度为桥梁设计中心线处腹板的高度。由于横隔板的间距比腹板的间距小，为计算横隔板受力，偏安全的将顶底板及顶底板加劲肋的重量加在横隔板上，纵梁单元通过调整自重系数只考虑腹板及腹板加劲肋的重量。悬臂自重加在边纵梁上并考虑其在边纵梁上产生的扭矩。

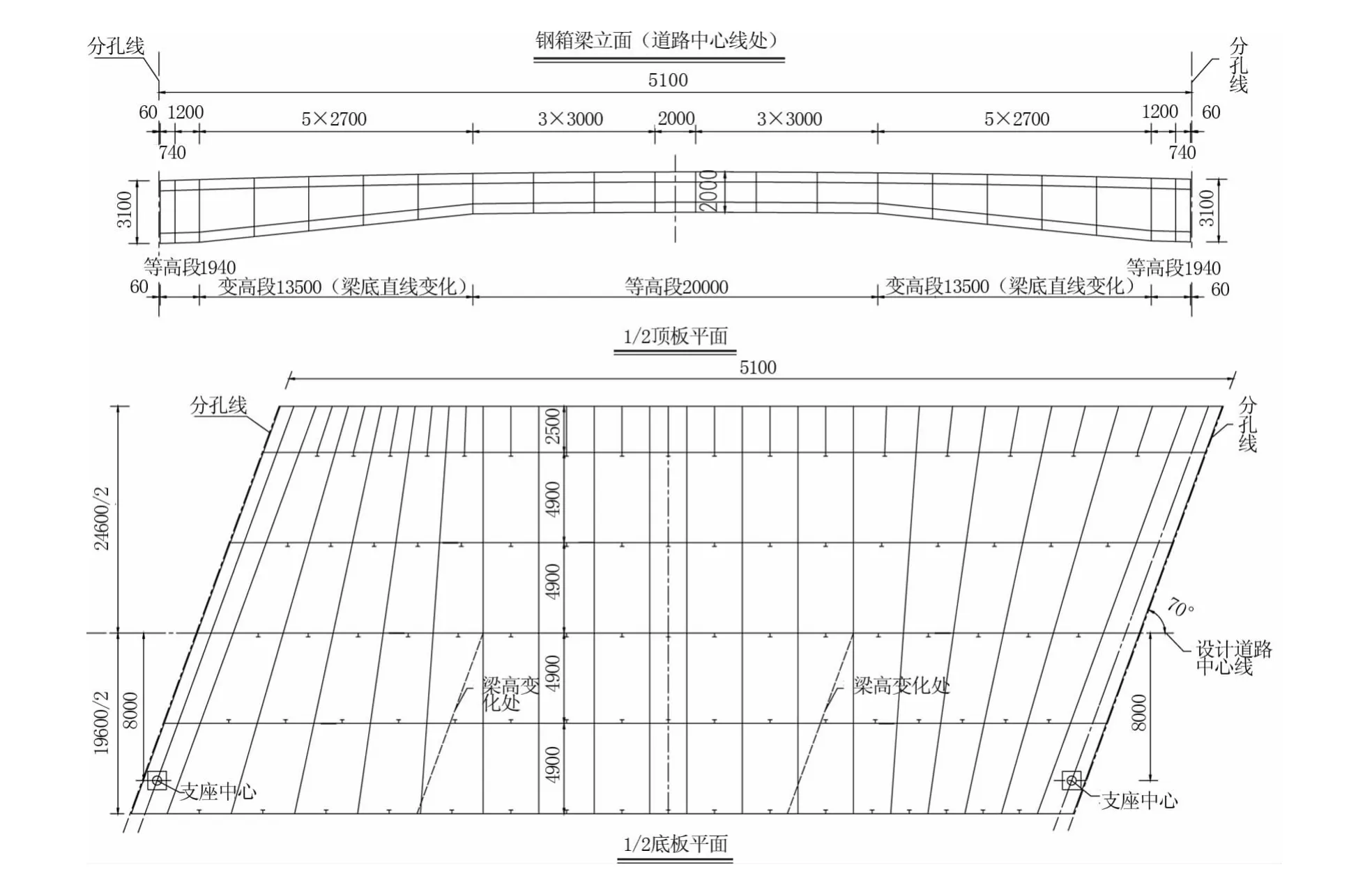
图2 总体布置图（单位：mm）

图3 空间单梁计算模型

图4 空间梁格计算模型

采用ansys10.0大型有限元分析软件，建立全桥空间板单元模型，顶底板、腹板、横隔板、纵向加劲肋均采用SHELL63单元类型，考虑横隔板人孔，不考虑横隔板的加劲肋，全桥共划分39 759个节点，42 240个单元。模型见图5（未示出顶板及顶板加劲肋）。

图5 空间板单元计算模型

3.2 计算结果比较

比较三种结构模型在自重作用下的支座反力、竖向挠度和下缘正应力的计算结果，见表1～表3。

表1 自重作用支反力结果比较表（单位：kN）

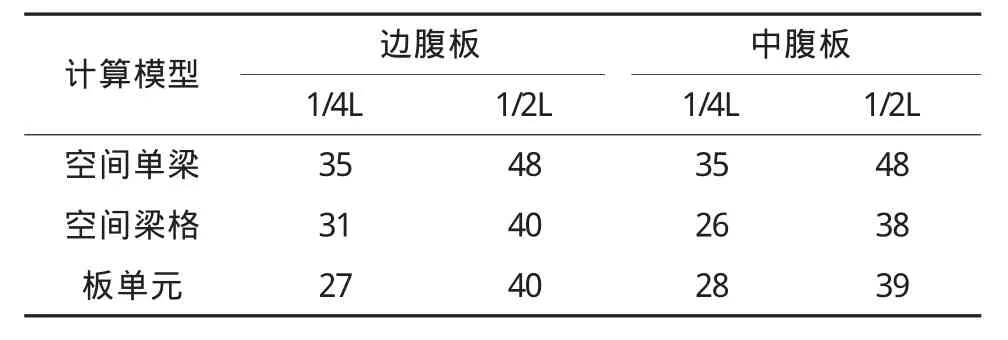
表2 自重作用挠度结果比较表（单位：mm）

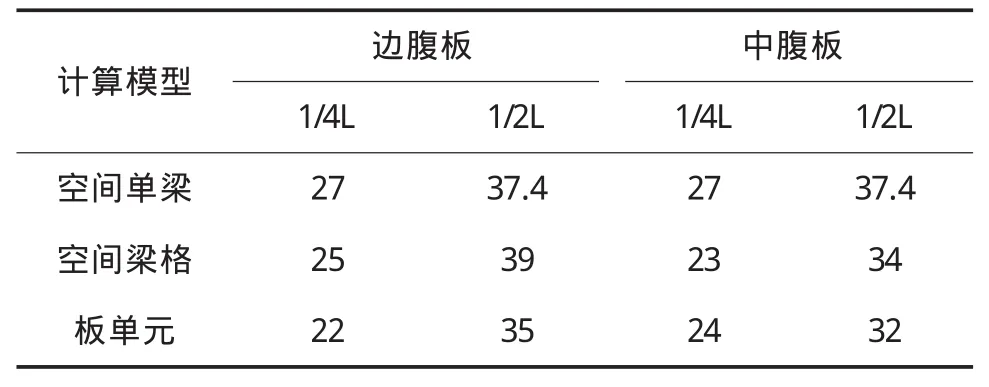
表3 自重作用下缘应力结果比较表（单位：MPa）

由以上分析结果可知，空间梁格模型和空间板单元模型计算结果较为接近，而空间单梁模型的计算结果与其他两个模型结构差异较大。空间单梁模型不能体现斜交箱梁中腹板和边腹板的受力不一致，横向支座反力分布不均，与实际结构受力不吻合。

4 结语

通过对斜交简支钢箱梁桥的三种计算模型结果的对比分析，可以得出如下结论：

（1）斜交箱梁的受力与正交箱梁有较大差异，利用传统的空间单梁模型分析会带来较大的误差，甚至得出错误的结果，而空间梁格模型和空间板单元模型分析结果比较接近。

（2）空间梁格模型分析斜交箱梁较为准确，可以方便的对此类桥型进行合理的设计。梁格分析的准确度取决于合理的梁格划分、设置虚拟横梁以及准确计算纵横梁的截面特性。

（3）梁格理论分析的不足之处是前处理工作量较大，对结构刚度的精确模拟相对具有一定的难度，且不能考虑剪力滞、扭转、箱梁畸变产生的截面翘曲，该理论有待更深入的研究与应用。

[1]范立础.桥梁工程[M].北京:人民交通出版社,1996.

[2]陈海滨.梁格法在异形钢箱梁桥技术分析中的应用[J].上海公路,2009(4):47-79.

[3]窦巍.梁格法在斜梁桥设计中的应用[J].山西建筑,2010(34):337-338.

[4]崔水花,王琪,刘庆振.剪力-柔性梁格法在钢桥中的应用[J].江苏建筑,2010(2):33-35.