基于状态约束的大规模正则表达式匹配算法

贺炜，郭云飞，扈红超

（国家数字交换系统工程技术研究中心，河南 郑州 450002）

1 引言

近年来，作为网络信息过滤、文字处理等应用中的关键组成部分，正则表达式匹配技术得到了快速发展。正则表达式匹配技术作为实现大规模模式匹配的主要手段，广泛应用于二进制序列分析、扩展标记语言处理及入侵检测系统中[1,2]。目前正则表达式匹配主要通过不确定性有限自动机（NFA,nondeterministic finite automata）以及确定性有限自动机（DFA, deterministic finite automata）来实现。

假设需要对k（k＞1）条正则表达式完成匹配，其中，第i（i=1,2,…,k ）条正则表达式中包含ni个字符。将k条正则表达式通过McNaughton-Yamada构造法转化为NFA后，会产生个NFA状态[3]，每输入一个字符，都需要对这些状态进行并行检测。上述特性导致基于NFA的正则表达式匹配在处理过程中的时间复杂度较高。虽然NFA能够通过硬件结构的加速来提高处理速率，但硬件加速方案通常缺少灵活性并且很难做到实时更新[4]。

针对NFA的缺点，另外一种解决方案是将NFA转化为DFA。通过将NFA中各个状态之间所有的有效转移存储在状态转移表（STT, state transition table）中，DFA可在硬件或软件平台中得到较好的实现。但是，基于DFA的正则表达式匹配也存在一些问题[5]。

1) 状态数爆炸：在最坏情况下，对于有n个状态的NFA，其最小等价DFA的状态数将达到O(2n)数量级。

2) 压缩时间代价：尽管STT可以通过消除相似状态冗余来压缩，但是现有压缩算法的时间复杂度至少为O(n2)。

NFA的空间特性较好，时间特性较差，而DFA相反，两者都不能很好地满足实际网络应用的需求。因此，快速高效是大规模正则表达式匹配的首要目标。本文将NFA、DFA两者优势相结合，提出了一种新的自动机构建算法Group2-DFA，在保持高速处理的前提下，缓解DFA状态爆炸的影响。本文首先通过分析状态爆炸现象，得出DFA状态爆炸的原因；然后根据状态间约束关系对NFA状态集合进行分组；第三步将每个NFA组转化为DFA，得到若干single-DFA，将各个single-DFA按照一定的方法组合，得到Group-DFA。由于Group-DFA处理速率较低，对Group-DFA进行二级分组，最终得到Group2-DFA。

2 相关工作

基于NFA的正则表达式匹配最初在集成电路中实现，随后SIDHU和PRASANNA将其部署在现场可编程门阵列（FPGA）中[6]。为了进一步提高系统的吞吐率以及资源利用率，FPGA实现中加入了许多优化措施，例如流水线、前缀提取、多字符匹配、字符编码等[7,8]。但是由于电路结构本身的缺点，在FPGA平台中，很难对基于NFA的正则表达式匹配进行及时更新。

基于DFA的正则表达式匹配可通过处理器架构来实现，相对于NFA，这种结构更加简单并易于操作。然而，状态爆炸问题导致算法对于内存的需求急剧增加，影响了内存性能和实际中部署的可行性。

为了解决DFA内存需求高的问题，目前常用的方法有2种：1）YU、PASETTO等[9,10]利用NFA的不确定性来压缩STT，以此达到较高的吞吐率性能。但是这类方法计算的复杂度较高，且大多依赖于特定的正则表达式集合特性。QI等[11]利用DFA状态的相似性压缩STT，提出FEACAN（front-end acceleration for content-aware network）算法，能够达到80%的压缩率。LIU等[12]提出的CSCA（cluster-based splitting compression algorithm）通过切分STT发现内在的冗余，能够达到95%的压缩率。但是FEACAN和CSCA算法都会降低系统的吞吐率。2）将大规模正则表达式匹配问题分解为若干小问题分别解决。ANTONELLO等[13]使用判决检验算法将m(m＞1)个正则表达式组合成g(m＞g＞0)个小组；WOODS等[14]将正则表达式切分为前缀和后缀2个组合，并且将所有的前缀构造为一个复合DFA，当到达DFA边界状态时，触发后缀匹配；YANG等[15]提出的SFA（semi-deterministic finite automata）算法采用NFA和DFA混合结构，在空间利用和吞吐率方面均有较好的效果。

3 理论基础

3.1 正则表达式匹配

定义1 对于正则表达式R，基于NFA的正则表达式匹配是在连续输入字符流的条件下，构造不确定性有限自动机M=(Q,Σ,δ,q0,F)，其中，Q是有限的NFA状态集合；Σ是有限的字母表；δ是不确定性状态转移函数，数量级为Q×Σ，大约为2Q；q0是状态机的初始状态，q0∈Q；F是状态机结束状态集合，F⊆Q。

定义2 对于正则表达式R，基于DFA的正则表达式匹配是根据标准构造方法，将相应的不确定性有限自动机M转化为确定性有限自动机M'=(Q',Σ, δ',q0,F ')，其中，Q'是有限的NFA状态集合，Q'⊆2Q；δ'是确定性状态转移函数，数量级为Q'×Σ；F'是状态机结束状态集合，F'⊆Q'；q0和Σ的定义与NFA中相同。

3.2 状态爆炸分析

YU等[9]证明了对于实际的正则表达式，NFA到DFA的转化会引起指数级别的状态爆炸，其等价最小DFA有2n个状态。为了更好地说明Group2-DFA原理，简要分析发生状态爆炸的原因。

对于正则表达式r1=/.*[a|b][c|d]{n -1}/.，构建NFA，命名为A。A中有初始状态q0、结束状态qn及n-1个中间状态{q1,…,qn-1}，各个状态间相互独立，互不影响。接收任意的输入，q0到达状态q1；接收输入a或b，q1到达状态q2；接收输入c或d，qi到达状态qi+1，1＜i＜n。

构造输入字符流，第一个字符为任意字符，第二个字符为a或b，之后的字符为c或d，各个字符之间相互独立不相关。当正则表达式r1接收到这一字符流时，对应的2n个状态均可能出现。将A转化为DFA后，至少会有2n个状态，与原有n+1个状态相比，呈指数级增长。

以上论述的基础是各个输入字符间相互独立，各个状态间互不影响，而在实际应用中，各个状态间存在相互约束，利用这种约束关系，可减小状态爆炸的规模。例如：状态q1、q2相互独立时，状态间约束不确定，存在4种状态组合(q1,q2)={(0,0),(0,1),(1,0),(1,1)}（标记1表示状态被激活）。若假设状态q1被激活时，q2一定被激活，则状态间约束关系确定，状态组合变为(q1,q2)={(0,0),(1,1)}2种，转化为DFA后，总状态数由2n+1减少为2n。以此类推，当各个状态间均有确定的约束关系时，可消除DFA状态爆炸的现象。

3.3 状态约束关系

根据状态爆炸分析可得出，若能确定状态间的约束关系，减少转化过程中的不确定性，则可大幅地减少DFA中的状态数。为描述状态间约束关系，引入3种集合关系：相交、包含、分离，具体定义如下。

定义3 记(q0,s)=q，其中，s为输入序列字符串；q0为初始状态，q为q0接收输入s后到达的目的状态。状态qx,qy∈Q，记Φx是满足(q0,s)=qx的输入序列s的集合，Φy是满足(q0,s)=qy的输入序列s的集合。

若Φx∩Φy=φ，则qx,qy互相分离，记为qx∩qy=φ。

若Φx∩Φy=Φx，则qx包含于qy，记为qx⊆qy。

若Φx∩Φy≠φ且Φx⊄Φy,Φy⊄Φx，则qx,qy相交。

当qx,qy分离时，约束关系确定，qx,qy不会被同时激活，在转化为DFA的过程中，不会引起状态爆炸。

当qx包含于qy时，qx被激活，qy一定被激活，不会引起状态增加；当qy被激活，qx不一定被激活，会引起一定的状态数增长。

当qx,qy相交时，2种状态相关性不强，可能同时被激活，也可能只激活一个，约束关系不确定，会引起状态爆炸。

根据定义的3种约束关系，提出NFA状态约束关系分析（NFA-SCA, NFA state constrain analysis）算法，可得到NFA状态集中任意2个状态之间的约束关系。图1中1）～8）通过分析状态转移路径，得到各个状态对应的输入序列集合Φ；9）～15）比较各个状态的输入序列集合，决定相互间约束关系的种类。NFA-SCA算法伪代码描述如图1所示。

图1 NFA-SCA算法

4 基于状态约束的Group2-DFA算法

4.1 NFA状态集合分组

为了降低状态数爆炸式增长对正则表达式匹配的影响，在NFA-SCA算法得到的状态间约束关系的基础上，按照以下原则将状态集合划分为若干小组：

1) 同一组内状态两两不相交；

2) 相交的状态放到不同的组内；

3) 每个组内包含尽可能多的相离和相互包含的状态。

依照上述原则分组可保证同一组内不会有相交状态，确定了状态间的约束关系，避免了大规模的状态增长。

划分过程步骤如下。

1) 初始化：建立状态集合V，包括所有NFA状态，置0m=。

2) 若V不为空，建立空集合mV。按状态序号，取V中一个状态tq，作以下判断：

①若mV为空，tq加入mV，并从V中删除tq；

②若mV不为空，将tq与mV中所有状态相比，若tq与这些状态都不相交，则tq加入mV，并从V中删除tq；否则，tq放回V中，尝试V中下一个状态，直到遍历V中的所有状态。记录Vm及其大小，m=m+1。重复2）直到V为空。

状态集合划分（SSD, state set division）算法的伪代码描述如图2所示。

图2 SSD算法

4.2 构建一级分组DFA(Group-DFA)

SSD算法可得到k个状态集合Vm,m=0,1,…,k ，每个Vm均有自身对应的状态集、字符表、转移函数、初始状态、结束状态，即对应于一个NFA，Mm=(Qm,Σ, δm,q0m,Fm)，其中，Qm是Vm中的状态集合；Σ是有限的字母表；δm是Vm中的状态转移函数；q0m是NFA的初始状态；Fm是NFA结束状态集合；

对于每一个Mm，按照标准构建算法转化为相应的等价DFA，即为Mm'，由于每个Mm中不包含相交的状态，所有每个Mm'中状态数增长较少。这样可得到k个独立的DFA，称为k个single-DFA。

每个single-DFA中包括2种状态转移：内部转移和平行转移。内部转移实现DFA内部的状态跳转，每个平行转移作为其他single-DFA的输入，激活另一个single-DFA中的状态；因此，single-DFA中的若干个状态都有可能同时被内部转移和其他single-DFA的平行转移同时激活，这种情况不满足DFA同一时刻只有一个激活状态的特性，为保证DFA的特性，添加多跳转关系综合判断逻辑，保留一个激活状态。

多跳转关系综合判断（MTA，multi-transition analysis）：按照single-DFA编号的大小，即m值的大小定义优先级：m值越小，single-DFA输出的平行转移的优先级越高。当一个single-DFA中的几个状态同时被激活时，选择优先级高的转移所激活的状态，其余状态不被激活。

构造Group-DFA时，每个single-DFA(i)最多有k个进位输出状态，以kbit长进位输出向量vector记录该输出状态。k个single-DFA最多同时有k个进位输出向量：vector(1),…,vector (k)，记录此k个向量值，共需要k×k大小的矩阵存储。

对于k个向量值，分析每个single-DFA会接收哪些平行转移，通过判断这些进位输出的优先级，即源DFA序号，确定保留哪一个平行转移作为输入。

MAT算法代码描述如图3所示。

图3 MTA算法

k个single-DFA间采用多跳转关系综合判断逻辑连接，都满足DFA的特性，组成的新DFA结构命名为Group-DFA。Group-DFA是NFA与DFA的混合结构，其中，各个DFA单独运行，DFA之间为并行操作，由同一个初始状态触发，相当于NFA中的各个状态，呈现NFA特性。

在最好的情况下，原始NFA中，各个状态都不相交，则构造的Group-DFA是一个单独的DFA；在最坏的情况下，各个状态相互之间都相交，则构造的Group-DFA仍然是原始的NFA。

4.3 构建二级分组DFA(Group2-DFA)

Group-DFA算法在实现过程中没有限制分组的数目。对于有N个状态的NFA，假设存在k个相交状态对，则会产生k个single-DFA。由于k个single-DFA之间呈NFA特性，k值过大将导致处理速率急剧降低。

为降低分组数量对处理速率的影响，设计二级分组结构如下。

1) 将k个single-DFA看作一个NFA中的k个状态。

2) 对该k个状态执行NFA-SCA算法，得到状态间约束关系。

3) 根据2）中的结果，执行SSD算法，对状态集合进行划分，得到二级分组集合。不同之处在于划分集合的数目限定为p个，若存在多于p个的相交状态，将多余的状态划入已知的p个集合中，得到二级分组集合。

4) 对3）中得到的p个NFA状态集合按照标准构建算法转化为p个DFA，称为Class2-DFA；并执行MTA算法，将p个Class2-DFA通过多跳转关系综合判断逻辑连接。

5) 在4）的结果中加入初始状态，二级分组DFA——Group2-DFA构建结束，Group2-DFA中包含p个Class2-DFA结构， Class2-DFA中的每个状态对应一个single-DFA。

Group2-DFA中包含3种转移关系：Class2-DFA的内部转移、Class2-DFA之间的平行转移和single-DFA的内部转移。Group2-DFA中同样存在多个DFA状态被同时激活的问题，按照single-DFA中的方式，根据编号大小来定义优先级，然后使用多跳转关系综合判断逻辑处理。

4.4 性能分析

有n个状态的NFA，时间复杂度为O(1)，空间复杂度为O(n)；构建Group-DFA后，有k个single-DFA，时间复杂度为O(k2)，空间复杂度为O(an)，其中，a为线性常数；构建Group2-DFA后，等价NFA结构有p个状态，且有两级的DFA逻辑结构，所以时间复杂度为O(2p2)，在p个二级集合中，每个集合最坏情况下有个相交状态，每一个状态代表一个single-DFA，定义为二级分割参数；将p个二级集合转化为p个DFA后，相比于Group-DFA，状态数会增加(2xx)倍，空间复杂度为，随着值的增加，Group2-DFA的空间复杂度增大，但时间复杂度减小，为了权衡时间和空间的代价，p值的选取需要根据实验结果和实际需求来确定。

5 实验仿真和性能验证

5.1 模型建立

针对Group-DFA中NFA、DFA混合的特点，设计处理模型如图4所示。

图4中，Group-DFA由若干个single-DFA单元以及多跳转关系综合判断模块（简称为综合模块）组成，single-DFA单元如虚线框内所示，包括状态查找表STT、状态合并、输入组合3个模块：输入组合以输入字符和当前状态作为输入，并将组合结果送入STT查询；STT根据输入数据得到相应的转移结果，若是内部转移，直接送入状态合并模块，若是进位转移，则送入综合模块；状态合并模块接收STT的内部转移以及综合模块得到的进位转移作为输入，决定在single-DFA内部选择哪一个转移状态作为当前状态。

综合模块实现MTA算法中的功能，分析处理各个single-DFA得到的进位转移结果。

对于Group2-DFA，二级分组结构包含p个DFA结构，每个DFA中的状态对应一个single-DFA，处理模型如图5所示。

5.2 性能仿真

性能分析采用的实验环境为：系统：Ubuntu 11.10；编译环境：gcc4.2.4；内存：2 GB；CPU：Intel双核。

实验数据采用snort24、snort31、bro217、dotstar300等4个规则集[16,17]。本节从空间存储消耗、系统吞吐率以及单字符平均内存访问次数3方面对算法性能进行分析，对比算法包括Group2-DFA算法、SFA算法、FEACAN算法以及CSCA算法。为了评价4种算法的性能，消除额外因素的影响，算法实现时，去掉了FEACAN算法中的硬件加速部分。

5.2.1 正则表达式规模与single-DFA数量关系

表1中给出了正则表达式规模与生成的single-DFA数量之间的关系，规模大小以正则表达式数量表示；采用NFA-SCA算法和SSD算法生成相应的若干single-DFA。

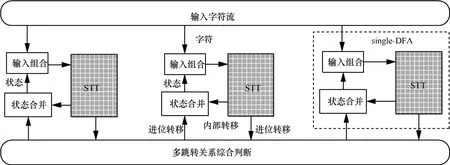
图4 Group-DFA处理模型

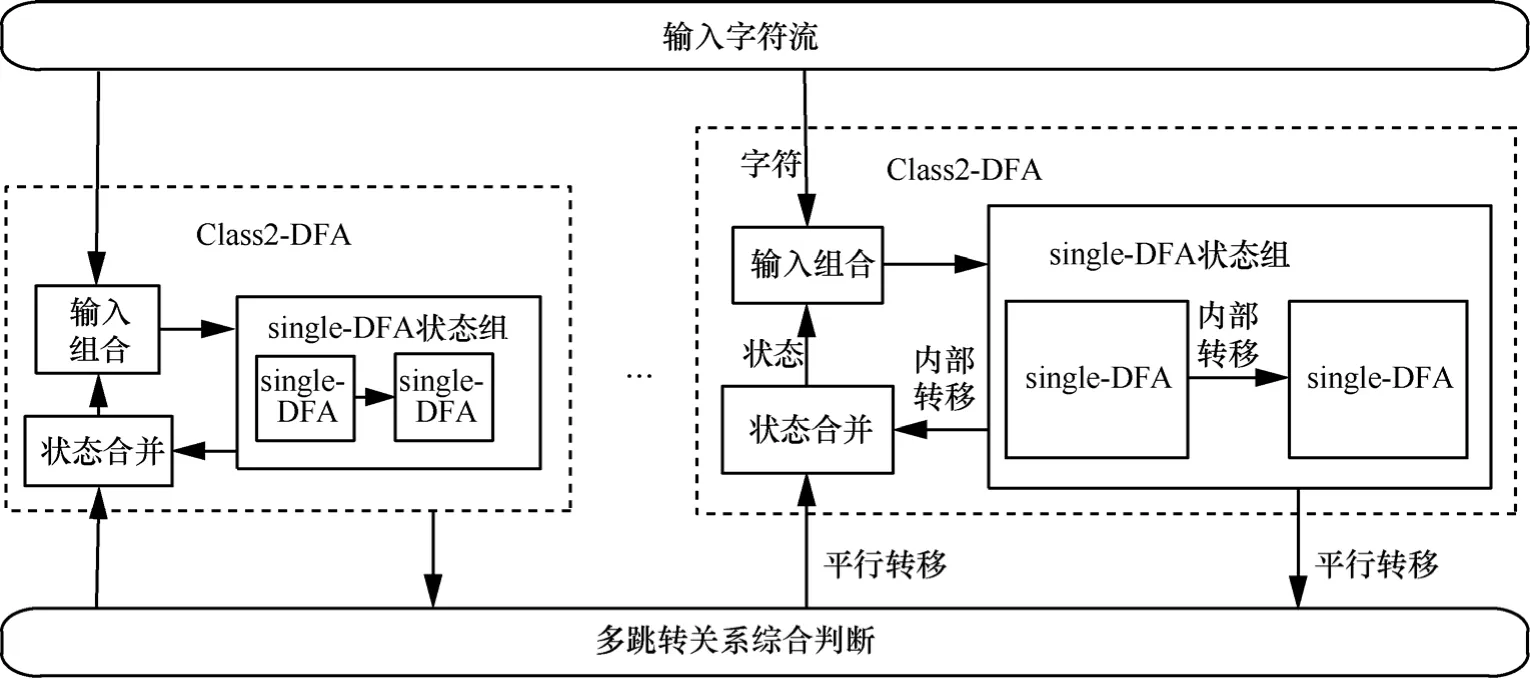
图5 Group2-DFA处理模型

表1 正则表达式规模与single-DFA数量关系

从表1中可看出，随着正则表达式规模的增大，NFA状态数也增多，各个状态之间的关系也更加复杂，出现了更多的相交情形，single-DFA的数量也随之增多。

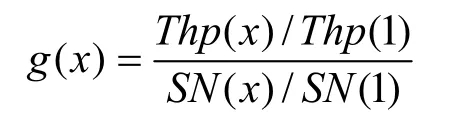
其中，Thp(x)为吞吐率函数，SN(x)为状态数函数，分别表示二级分割参数为x时的系统吞吐率和状态数。其中，x=1时，表示不进行分割，Group2-DFA就是Group-DFA。由性能增益函数g(x)的定义可知，g(x)是以x=1时的吞吐率Thp(1)和状态数SN(1)为标准，将Thp(x)和SN(x)归一化后的比值，表示随着x的变化，吞吐率和状态数增长的效果。

在snort24、bro217和dotstar300 3种规则集下，分别计算Group2-DFA的状态数以及吞吐率如图6所示。

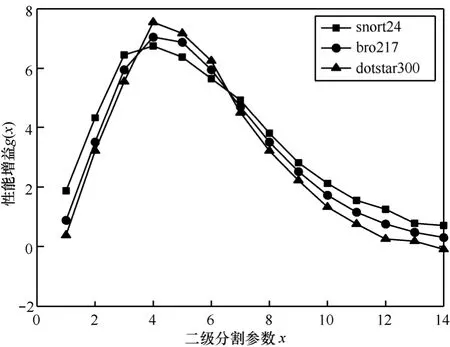
图6 性能增益随分割参数的变化

从图6中可看出，对于不同的规则集，x=4时，性能增益均达到最大值，说明此时吞吐率增长较大，状态数增长相对较小，整体性能达到最佳。

面对不同的实际应用，对于空间性能要求较高时，可减小分割参数；对于吞吐率性能要求较高时，可增大分割参数，以达到合适的效果。

5.2.3 空间存储性能与系统吞吐率

空间存储占用与状态数量呈正比，因此分析算法生成的状态数可反映空间存储的性能。实验中实现了基于SFA算法，FEACAN算法、CSCA算法以及Group2-DFA算法的正则表达式匹配，根据5.2.2节的实验结果，Group2-DFA算法的二级分割参数取x=4。正则表达式规则选用snort24、bro217和dotstar300的混合集合，规则数量从24开始逐渐增加，最多选取300条正则表达式。

4种算法的状态数对比情况如图7所示。正则表达式规模较小时，4种算法得到的状态数差别较小；随着正则表达式规模的增长，Group2-DFA算法的状态数增长最慢，近似呈线性增长，而SFA算法、FEACAN算法以及CSCA算法的状态数增长较快，可以看出，Group2-DFA算法在减少状态数方面的优势较为明显。

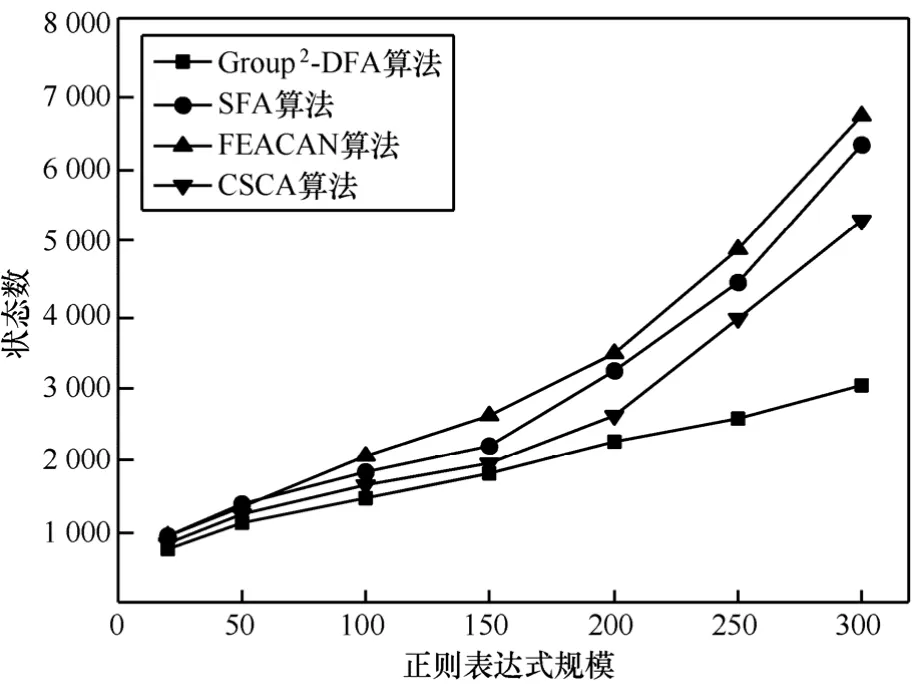
图7 4种算法状态数对比

表2给出了4种规则集合下，Group2-DFA相对于DFA的状态减少率。

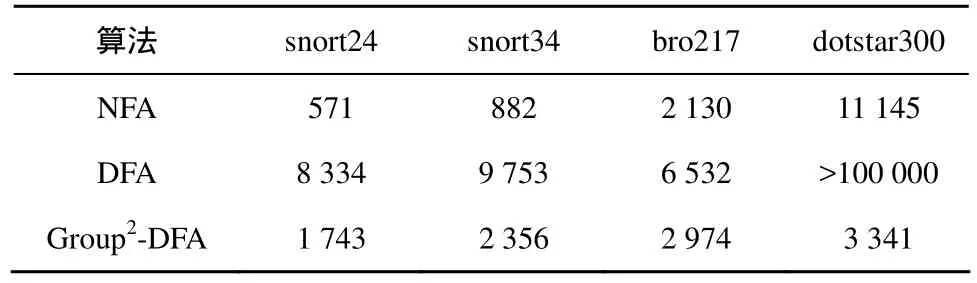
表2 正则表达式集合下Group2-DFA的状态减少率

根据表2计算可得，对于4个不同的规则集合，Group2-DFA的状态减少率分别为：79.1%、75.9%、54.4%以及大于96.6%。

正则表达式集合bro217中，处于相交关系的状态较少，状态爆炸不明显，Group2-DFA算法对于状态数的减少百分比较小；测试中，Group2-DFA算法对于snort集合、dotstar_300集合的性能较好，能达到75%以上。另外，由于dotstar_300生成的DFA数目大于1×105个，超出预设的内存占用，没有得到全部的DFA状态数。

图8给出了4种算法的吞吐率（Gbit/s）对比情况。从图8中可以看出，随着正则表达式规模的增加，Group2-DFA算法的吞吐率较为稳定，这是由于Group2-DFA算法的吞吐率主要受到并行等价NFA数量的影响，与参数x的选取有关，与正则表达式规模无关。Group2-DFA算法的吞吐率与SFA算法较为接近，相差较小，但Group2-DFA算法的浮动较小，比SFA算法稳定。而FEACAN和CSCA的吞吐率受正则表达式规模的影响较大，虽然在正则表达式规模较小时，两者的吞吐率高于Group2- DFA算法，但是随着正则表达式规模的增加，吞吐率呈下降趋势，当正则表达式大于250条时，其吞吐率小于Group2-DFA算法。

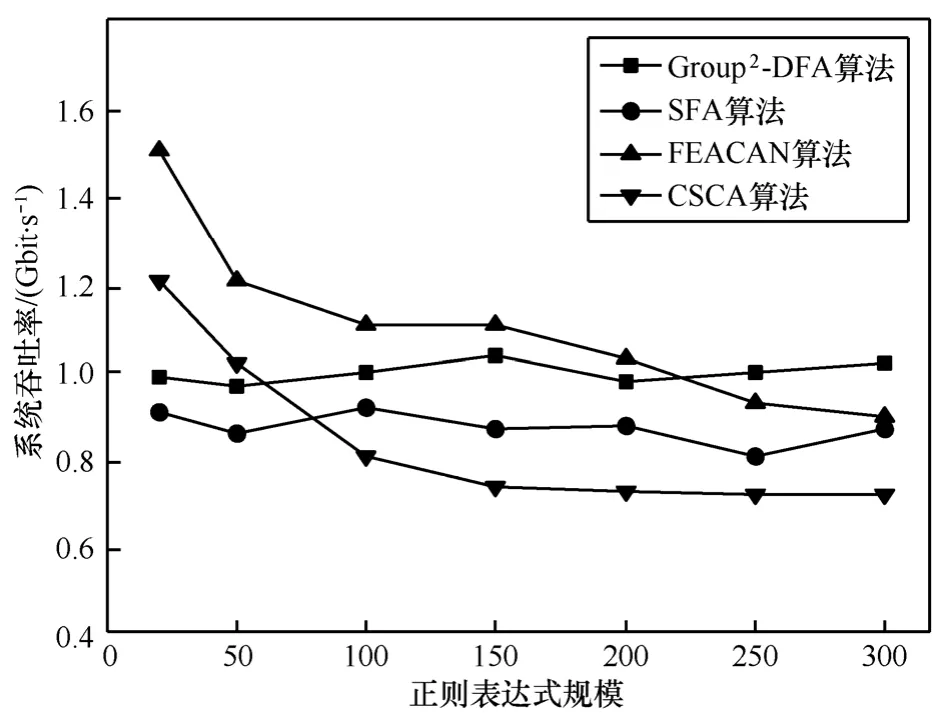
图8 4种算法的吞吐率对比

图9给出了4种算法处理一个字符时的平均内存访问次数。可以看出，在处理一个字符时，Group2-DFA算法需要访问多次内存，时间复杂度有所增长，高于其他3种算法。这是由于Group2-DFA算法中包括两级分组结构，每一级中都包括NFA和DFA 2种形态，而NFA和DFA的状态转移表需要单独存储，导致处理字符时，可能需要读取多次内存。虽然Group2-DFA算法的时间复杂度有所增长，但由于采用二级分组结构，充分利用了DFA的快速处理特性，所以Group2-DFA算法仍然可以达到较高的吞吐率。

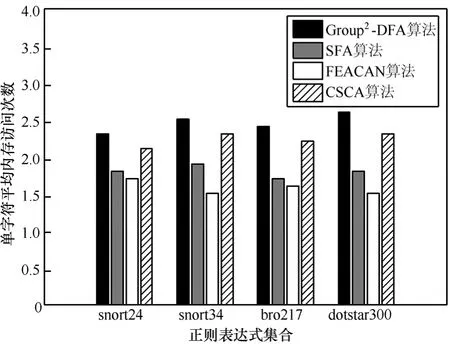
图9 单字符平均内存访问次数

实验结果表明，Group2-DFA算法的状态数小于SFA、FEACAN、CSCA算法；当正则表达式规模增加时，Group2-DFA算法的吞吐率稳定在较高水平；对于不同的规则集合，Group2-DFA算法的单字符平均内存访问次数高于其他3种算法。综上所述，根据性能增益合理选取分割参数后，Group2-DFA算法能够达到较好的状态减少率，并且保持较高的系统吞吐率，付出的代价是单字符平均内存访问次数有一定的增加。

6 结束语

本文提出的Group2-DFA算法结合NFA的空间和DFA的时间特性，以一定的时间复杂度为代价，减小了DFA的空间复杂度。算法通过分析NFA转化为DFA过程中产生状态爆炸的原因，引入了一种状态分类方法，构建二级分组模型，在保证系统吞吐率的前提下，有效地减轻了状态爆炸的影响。在系统结构上，Group2-DFA算法呈现NFA的并行处理特性，在内部实现中，采用单独的DFA处理；这种混合结构使得Group2-DFA算法能够通过多核技术实现并行加速，有效地提升了系统的吞吐率。

对于大规模的正则表达式集合，分组得到的single-DFA数量较多，会降低系统处理的性能，进一步的研究可考虑对分组的方法进行改进，以提高处理速率。另外，由于采用单字符输入的方法，处理速率受到一定的限制，为了达到更高的系统吞吐率，可引入多字符处理机制来满足实际需求。

[1] JIANG L, TAN J, LIU Y. ClusterFA: a memory-efficient DFA structure for network intrusion detection[A]. Proceedings of the 7th ACM Symposium on Computer and Communications Security Information[C]. New York,USA, 2012. 65-66.

[2] BECCHI M, CROWLEY P. Efficient regular expression evaluation:theory to practice[A]. Proceedings of the 4th ACM/IEEE Symposium on Architectures for Networking and Communications Systems[C].Colorado: ACM, 2008. 50-59.

[3] YANG Y H E, JIANG W, PRASANNA V K. Compact architecture for high-throughput regular expression matching on FPGA[A]. Proceedings of the 4th ACM/IEEE Symposium on Architectures for Networking and Communications Systems[C]. San Jose, California,USA,2008.30-39.

[4] ZHENG K, ZHANG X, CAI Z, etal. Scalable NIDS via negative pattern matching and exclusive pattern matching[A]. Proceedings IEEE International Conference on Computer Communications, Joint Conference of the IEEE Computer and Communications Societies[C].San Dieg, 2010. 1-9.

[5] 李奇越. 网络内容分析中基于硬件的字符串匹配算法的研究[D].合肥: 中国科技大学, 2008.LI Q Y. String Matching Algorithm Research based on Hardware in Network, Content Analysis[D]. Hefei: University of Science and Technology of China, 2008.

[6] LIN C H, HUANG C T, JIANG C P,etal. Optimization of regular expression pattern matching circuits on FPGA[A]. Proceedings of Design, Automation and Test in Europe[C]. Germany, 2006. 1-6.

[7] LE H, PRASANNA V. A memory-efficient and modular approach for large-scale string pattern matching[J]. IEEE Transactions on Computers, 2013,62(5):844-857.

[8] BECCHI M, CROWLEY P. A hybrid finite automaton for practical deep packet inspection[A]. Proceedings of ACM CoNEXT Conference[C]. New York,USA, 2007.1-12.

[9] YU F, CHEN Z, DIAO Y, etal. Fast and memory-efficient regular expression matching for deep packet inspection[A]. ACM/IEEE Symposium on Architecture for Networking and Communications System[C]. San Jose, California,USA, 2006. 93-102.

[10] PASETTO D, PETRINI F, AGARWAL V. Tools for very fast regular expression matching[J]. Computer, 2010, 43(3):50-58.

[11] QI Y, WANG K, FONG J, etal. FEACAN: front-end acceleration for content-aware network processing[A]. Proceedings of 30th IEEE International Conference on Computer Communications, Joint Conference of the IEEE Computer and Communications Societies[C].Shanghai, China, 2011. 2114-2122.

[12] LIU T, YANG Y, LIU Y, etal. An efficient regular expressions compression algorithm from a new perspective[A]. Proceedings of 30th IEEE International Conference on Computer Communications, Joint Conference of the IEEE Computer and Communications Societies[C].Shanghai, China, 2011. 2129-2137.

[13] ANTONELLO R, FERNANDES S, SADOK D, etal. Deterministic finite automaton for scalable traffic identification: the power of compressing by range[A]. Network Operations and Management Symposium (NOMS)[C]. Piscataway:IEEE, 2012. 155-162.

[14] WOODS L, TEUBNER J, ALONSO G. Complex event detection at wire speed with FPGAs[J]. The VLDB Endowment, 2010, 3(1-2):660-669.

[15] YANG Y H E, PRASANNA V K. Space-time tradeoff in regular expression matching with semi-deterministic finite automata[A]. Proceedings of 30th IEEE International Conference on Computer Communications, Joint Conference of the IEEE Computer and Communications Societies[C]. Shanghai, China, 2011. 1853-1861.

[16] Sourcefire, SNORT[EB/OL].http://www.snort.org/snort-downloads, 2012.

[17] International computer science institute, bro intrusion detection system[EB/OL]. http://bro-ids.org/download/index.html, 2012.