数学分析中的矛盾问题研究
2013-08-06梁江波
梁江波
(延安大学 西安创新学院理工系,陕西 西安 710100)
在数学分析中,对矛盾问题和对立理论的分析,既有助于人们对数学思维、理论构造以及思维方式的研究,而且有助于人们对数学史和评价标准的深入探讨.因此,对数学分析中的矛盾问题研究的探讨有其重要的科学价值和意义.
1 数学分析中存在的若干矛盾
数学分析(Mathematical Analysis)是数学专业的必修课程之一,基本内容是微积分,但是与微积分有很大的差别.数学分析的基础是实数理论.实数系最重要的特征是连续性,有了实数的连续性,才能讨论极限,连续,微分和积分.正是在讨论函数的各种极限运算的合法性的过程中,人们逐渐建立起严密的数学分析理论体系.在这里主要针对数学分析中存在的若干矛盾进行简单分析,大体有以下几种情况:
1.1 整体与局部
在数学分析中,整体与局部是一对比较重要的矛盾关系.整体和局部的辨证关系原理原理内容:任何事物都有它的整体和局部.整体和局部二者既相互区别又相互联系,整体处于统率的决定地位;局部也制约着整体,甚至在一定条件下关键部分的性能对整体起决定作用.因此,在分析与研究时,要求要树立全局观念,办事情从整体着眼,寻求最优目标;又要搞好局部,使整体功能得到最大发挥.
微积分中局部与整体的矛盾关系
局部与整体的思想贯穿微积分的始终,该思想在微积分中有着深入的体现.微分和积分都就是用局部代替整体的思想,从而化曲为直,化变量为常量.微分是求商,积分是求积(和).因此,要正确把握该思想,掌握局部与整体思想在现实生活中的重要意义,并且在实际研究中,根据明清河的《数学分析的思想与方法》(山东大学出版社,这本书对微积分的思想有很深的阐述)和克莱因著《古今数学思想》进行全面分析与总结,例如以下命题:
(4)f(x)的原函数为F(x),且F(x)是以T为周期的函数,则
这里主要讲到的是微积分基本定理.
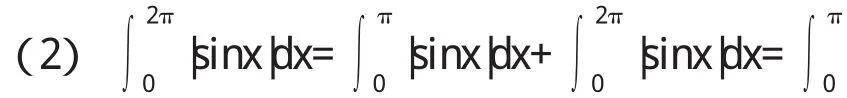

(3)根据函数导数运算性质,若F'(x)=1x,应有-F(x)=lnx+c-(c为常数),结论错误.
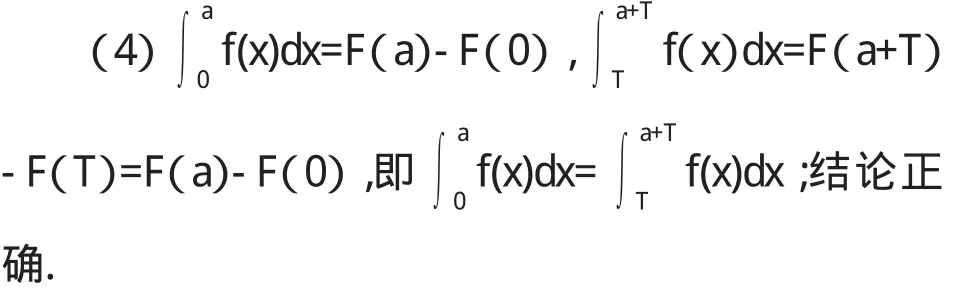
在处理这些问题时,正是运用了其整体与局部的矛盾关系,结合微积分基本定理,问题得到全面解决.
1.2 离散与连续
——离散与连续在数学分析中,是一对对立统一的关系.其中,最为明显的就是级数与积分的转换、数列与函数之间的相互转换.在数学分析中,函数极限与数列极限是分别定义的,而实现这两者之间的相互转换的理论桥梁正是海涅定理.
在处理微积分的过程中,离散型的数据或者类型通常采用连续函数来描述,连续函数主要通过不连续的函数来近似处理,所以,它们在数学中,经常是成对出现的.收敛和极限存在是同一回事.可导必连续,连续比极限存在(收敛),收敛必局部有界.反之都未必.连续必有定义,有定义未必连续.有定义与极限,局部有界没有任何关系.可积不同,是一个整体概念,不能谈局部.可以这么说,可积则函数在整个定义域上有界,但有界未必可积.有界闭区间上的连续函数必可积,但可积不一定连续.
例如:如果一个随机变量X所有可能取到的值是有限个或者是可列无限多个,并且以确定的概率取这些不同的值,成为离散型随机变量例如X=1,2,3,……n如果对于随机变量X的分布函数F(X)存在非负函数f(x)使得对于任意实数x有F(x)=∫f(t)dt,积分下限是负无穷,上限是x,则称X为连续性随机变量
1.3 常量与变量
在数学分析中,常量是静止不动的,是不变的,而变量则是不断变化的量,是运动着的,它们是一对对立的关系.根据相对理论分析,知道,所有的事物都是不断运动的,所以,常量的静止不动与不变是相对于变量而言的.变量通常情况下,要通过常量来体现,而常量又通常位于变量之中,因此,这两者在一定的情况与条件下,是可以相互转化的,从某种角度上讲,这两者之间又是一个统一体.也正是因为如此,在数学分极中,这种数学思想帮助人们解决了很多重要问题和理论问题.
1.4 有限与无限
在数学分析中,有限与无限这两个概念是截然对立的,在实际处理中,无限中包含着有限,而无限又可以从中有限中找到,从这个角度来分析,充分体现了无限与有限的对立与统一.在学习微积分时,学生所接触到的第一概念就是极限,也是一个非常重要的概念,但是在教学中,极限理论的学习一直都是一个研究的热点和学习和难点问题,在学习中,一旦脱离两者之间的辩证关系,只是从纯数学的角度去分析,这样会给学生学习造成很大的困难,而且也不利于对微积分问题的分析与研究.
另外,在数学分析中,有限开覆盖定理就是描述的关于无限及有限的问题.有限开覆盖定理(Heine-Borel定理)主要描述的是欧氏空间局部的紧性,这个性质在拓扑里应用比较普遍,这个定理本身也不是很直观.简单来讲,就是微积分本身从有限到无限的一次飞跃,但是技术上很多无限的问题仍然需要转化为有限的问题才能解决,从有限开覆盖定理的叙述就可以看出,该定理可以实现从无限到有限的归约.该定理另一个用途是在于从局部向整体的归约,只要把每一点局部的性质分析清楚了就可以推广到整个区域上,这一点也体现了微积分的核心.例如:
若 y(n+1)>y(n);lim yn->∞;lim(x(n+1)-x(n))/(y(n+1)-yn)存在,那么lim xn/yn=lim(x(n+1)-x(n))/(y(n+1)-yn).
分析:lim(x(n+1)-x(n))/(y(n+1)-yn)存在
设lim(x(n+1)-x(n))/(y(n+1)-yn)=a
对于任意e>0,存在N使得,对n>N有|(x(n+1)-x(n))/(y(n+1)-yn)-a| 那么对于n>N,有 a-e<(x(n+1)-x(n))/(y(n+1)-yn) 那么 (a-e)(y(N+2)-y(N+1)) (a-e)(y(N+3)-y(N+2)) … (a-e)(y(n+1)-yn) (a-e)(y(n+1)-y(N+1)) 故 |(x(n+1)-x(N+1))/(y(n+1)-y(N+1))-a| 现在要转化xn/yn为含有上式的形式,并证明其极限xn/yn-a=(xn-x(N+1))/(yn-y(N+1))*(yn-y(N+1))/yn+(x(N+1)-a*y(N+1))/yn, 根据上式: |xn/yn-a|<=e|1-y(N+1)/yn|+|(x(N+1)-a*y(N+1))/yn|<=e+|(x(N+1)-a*y(N+1))/yn|, 存在N'>N使得对n>N'有|(x(N+1)-a*y(N+1))/yn| 那么lim xn/yn=lim(x(n+1)-x(n))/(y(n+1)-yn)这个理论证明,直观地分析了有限与无限的关系. 首先,要以几何直观做启发,大胆想象,严密论证.数学分析的一个特点是高度抽象性,而且几何直观确实不能代替严密的证明,但一味的强调抽象性,容易迷失方向,而几何直观对许多分析定理有启发作用.很多定理可以从几何直观中观察出来,加以提炼,最后严格证明而上升为定理.如费马引理,即可导函数的极值点处导数值为0,几何直观上,一个可导函数在极值点处的切线应该是水平的,而且似乎不一定要求导函数连续,然后通过分析严格证明的猜想. 但是,问题还可提升高度,上面说可导函数极值点导数为0,那么可以分析一下导数为0是否就是极值点,什么时候有极值点,导数为0点未必就是极值点.至于后一个问题,条件可能不止一个.其中有一个比较特殊,知道闭区间上的连续函数必有最大值和最小值.而对于非常数函数,如果最值在区间内部取得,它也是极值,如果f可导,则f'(x0)=0.于是转到什么时候可以有内部最值(也是极值).一个条件是非常数可导函数的两端点相等,则区间内部必有最值点,因而有内点x0满足f'(x0)=0,于是就有了罗尔定理.又问了,这个条件必要吗?可以举出反例,这说明罗尔定理的条件只是充分条件.类似的几何直观还很多,比如把图象旋转一下,罗尔定理就变成了拉格朗日定理,如果用参数形式表示拉格朗日定理,则就变成了柯西定理.当然,以上只是从几何直观做出的猜想,接下来必须严格的给予证明. 其次,要从多角度思考问题.在解决了一个问题后,可以再挖掘一下,从中找到新的发现,如条件和结论对调,结论是否还成立,原问题要求函数f连续,我换成Riemann可积后,结论如何;或者说原问题是与三角函数(涉及周期性)有关,换成一般的周期函数后,结论如何.比如关于积分号下取极限(or积分运算与极限过程互换)期函数代替三角函数推广下.(这种推广不一定都行的通,只是提供一种可能的思路) 总而言之,在数学分析中,要加强矛盾问题的分析,深入探讨其中存在的矛盾结论,从研究方法以及评价标准等各个方面分析,进行对数学分析中存在的矛盾有一个全新的认识. 〔1〕董治强.浅析数学分析中的若干矛盾[J].佳木斯教育学院学报,2012(1):87,98. 〔2〕杨莉.数学分析中的否定判断浅谈[J].昆明冶金高等专科学校学报,2005,21(3):96-100. 〔3〕谢巍.潜无穷、实无穷与数学分析[J].四川理工学院学报,2005,18(3):96-98. 〔4〕谢太光.再探数学分析教学难问题[J].西南师范大学学报,2009,30(6):1142-1146. 〔5〕郭艳慧.数学分析中的辩证法[J].南昌教育学院学报,2011,26(9):50-51.2 掌握数学分析中矛盾问题的学习方法
3 总结
