基于Stackbelberg博弈的认知无线网络速率控制模型

1.闽江学院 计算机科学系，福州 350108

2.富春通信股份有限公司 通信技术研究院，福州 350003

1.闽江学院 计算机科学系，福州 350108

2.富春通信股份有限公司 通信技术研究院，福州 350003

1 引言

随着无线通信新技术不断的涌现，使得无线频谱资源需求快速增长。可用频谱资源数量有限及频谱资源的浪费加剧了无线频谱缺乏的问题。FCC（Federal Communications Commision）的研究报告表明在给定区域和时间频普利用率大约仅为30%[1]。为解决频谱欠利用及缺乏问题，业界提出了认知无线电的概念。

由于认知无线电固有的分布式共享无线资源特征，因此可用博弈论[2]来研究认知无线电网络的资源共享及分配问题。在应用博弈论研究认知无线电网络的频谱共享及分配的方面，文献[3]应用重复博弈模型研究了认知无线电网络的频谱共享问题，假设网络中存在自私行为及非对称结点的情况下，研究了如何保证分布式环境下的频谱分配效率及公平性。文献[4]应用非合作博弈研究了分布式环境下的认知无线电网络的信道选择及频谱访问问题，重点分析了频谱访问模型的纳什均衡存在性并相应地给出纳什均衡的求解算法。应用其他不同博弈模型研究认知无线电网络频谱分配和共享的可见文献[5-7]等。在应用博弈论研究认知无线电网络的功率分配及控制方面，文献[8]应用势力场博弈研究了认知无线电网络功率分配问题，提出基于势力场博弈的认知无线电网络功率分配算法，提出的功率分配算法能较好地保障用户间功率分配的公平性。文献[9]应用非合作博弈研究了频谱共享的多信道认知无线电网络中分布式功率分配问题，分析了主用户访问保护约束下的多信道功率分配问题纳什均衡的存在性和唯一性，提出了分布式多信道功率分配算法以获取最优功率分配。文献[10]应用Stackelberg博弈研究认知无线网络功率和信道共同分配的问题，并提出了基于迭代的最优功率及信道联合分配算法。文献[11]应用Stackelberg博弈模型研究了基于机会频谱访问的认知无线电网络频谱共享问题从而提升频谱所有者的收益。文献[12]应用Stackelberg博弈研究了协作认知无线电网络频谱感知策略。

2 基于Stackelberg博弈的认知无线单跳网络流量速率控制模型

2.1 认知无线单跳网络结点速率模型

假设认知无线单跳网络用户和主用户M共享特定的无线频谱来进行通信，认知网络中有N={1，2，…，N}个认知用户与认知无线接入点通信，其中网络拓扑示意如图1所示。假设每个认知用户都是使用基于IEEE 802.11分布式协调功能（DCF）协议来访问信道且每个结点都有相同的概率获得信道分配。假设无线接入点在捕获频谱空洞后每个认知结点都有不间断的流量通过无线接入点进行业务通信，进一步可假设网络中的认知结点使用IEEE 802.11标准中的避退参数都是一致且发送数据包大小都为L，则网络中认知结点可获得的吞吐率可写为如下所示表达式[14]：

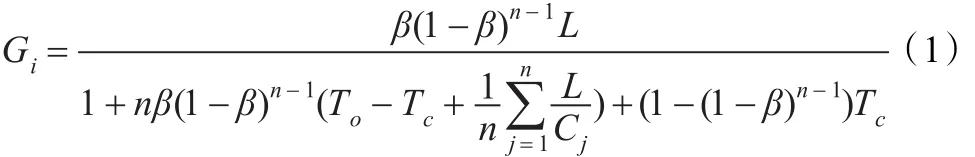
其中参数Cj表示传输结点所使用物理层传输速率，参数To表示传输时隙帧的串音，参数Tc表示RTS冲突时隙的固定串音，参数 β表示在总传输次数中每个结点在每一个避退时隙中平均尝试传输速率，其可表示为参数n和指数避退

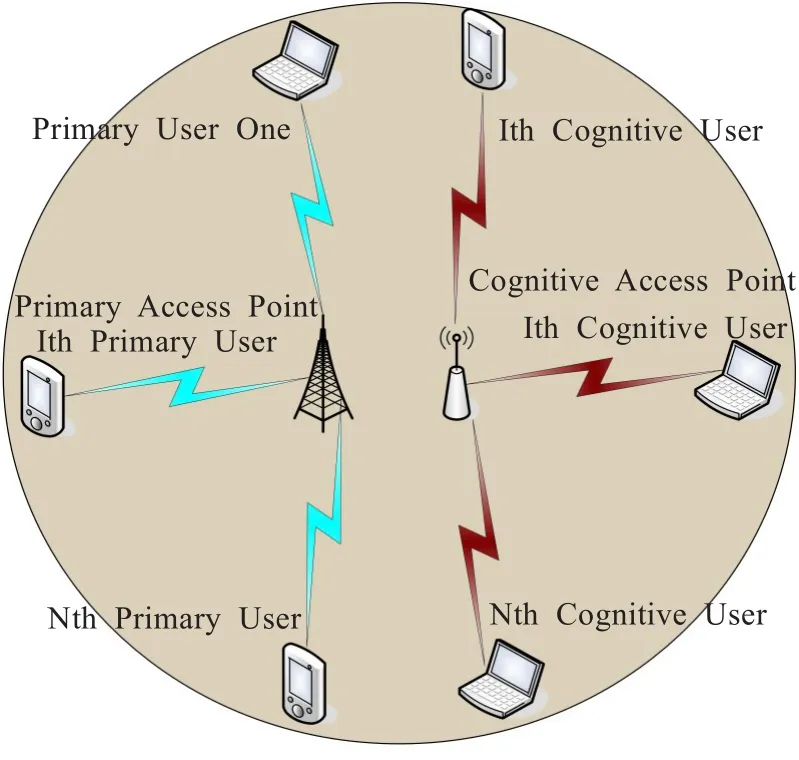
图1 认知无线单跳网络示意图

乘子 p的函数，参数β的具体表达式如下所示：

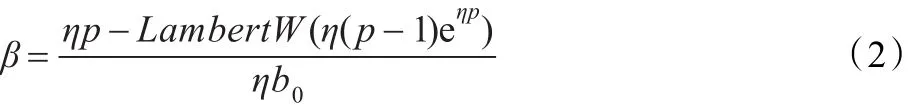
其中上述表达式中参数η可表示成η=(n-1)/b0，LambertW是朗伯W函数，关于式（1）更详细的描述可参见文献[14]。

在认知无线单跳网络中，网络中结点需要不间断地感知频谱访问机会，进而捕获无线信道才能获得与用户通信服务的机会。假设无线接入点感知频谱空洞后立即发送信号给认知结点并与之进行交互通信，而认知用户接收到可以通信的信号后立即自适应地采取数据传输速率进行通信。上述通信过程可以描述成典型的Stackelberg博弈模型，博弈信号发送方（博弈领头者）即为认知无线接入点，博弈信号接收方（博弈追随者）即为网络中的所有认知用户。因此可以用Stackelberg博弈模型来对认知无线单跳网络流量速率分配问题进行建模和分析。

2.2 认知无线单跳网络流量速率控制Stackelberg博弈模型

认知无线网络中无线接入点是认知结点通信业务流量的服务提供者，假设无线接入点i为认知结点提供的每单位数据传输速率价格为λi，如果认知结点i传输数据速率为Cj，则其支付总费用为λiCj。无线接入点的总收入即为给网络中所有结点提供服务所获的收益之和，其可写成参数为结点i的价格λi和传输数据速率Cj的表达式：

其中结点价格向量 λ=(λ1，λ2，…，λN)，结点速率向量 C= (C1，C2，…，CN)。

假设认知结点的效用为结点所获吞吐率G的线性函数，则可以定义结点的效用函数如下所示：

其中加权因子αi(αi＞0)表示认知结点传输每单位数据所获吞吐率收益，αi值越大表示认知结点效用受加权因子影响更敏感。认知结点所获收益减去支付给无线接入点成本即为结点的总收益。由于无线网络固有的分布式特征，因此可以假设认知结点都理性地、自私地且非合作地最大化结点的自身效用。上述过程可以用非合作博弈模型来描述，即在无线接入点给定一个价格向量λ的基础上（该价格向量表示结点传输数据速率向量为C时的成本），对于网络中所有认知结点来说，认知结点i必须针对无线接入点制定的价格 λi(λi＞0)选择相对应的传输数据速率Ci以期最大化结点自身的收益，其用数学表达式可描述为如下所示的表达式：

其中C-i表示除结点i之外的其他结点流量的数据传输速率。

对于无线接入点而言，其目标是通过制定的最优价格策略来最大化自身总收益，即最大化式（3）。而对认知结点而言，其根据无线接入点制定的价格选择最优数据传输速率来最大化结点个体收益，即最大化式（5）。因此上述模型可描述为典型的Stackelberg博弈模型，其中无线接入点作为博弈领头者，其通过设置价格向量给不同认知结点提供服务，而认知结点可看作博弈的追随者，其根据服务提供者即无线接入点设置的价格向量来自适应地最大化结点自身效用。因此作为服务提供的无线接入点的目标是寻找相应的价格向量 λ*=(，…，)，使得最大化如下表达式：

认知无线单跳网络流量速率控制Stackelberg博弈模型

博弈领头者：认知无线接入点

领头者博弈策略：λ（即制定相应的价格向量），博弈参与者策略的空间为[0，+∞]

博弈追随者：认知网络中的无线结点

追随者博弈策略：Ci（认知结点传输速率），其策略空间同样为[0，+∞]

追随者效用函数：U(λi，Ci)=αiGi- λiCi，其中

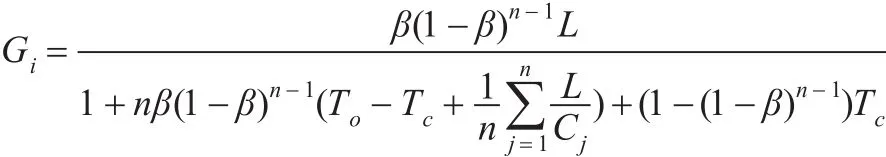
定义1假设C*=(…，)是式（5）的解，λ*= (…，)是式（6）的解。则 (C*，λ*)是认知无线单跳网络流量速率控制的Stackelberg博弈模型纳什均衡其必须满

根据上述定义Stackelberg博弈模型可知模型的纳什均衡解不仅可以最大化无线接入点效用而且还能在给定价格向量基础上最大化结点的自身效用，因此在该纳什均衡点处博弈模型中的任一博弈参与者都无法通过改变博弈策略而获取更高收益。根据上述描述可以给出提出的博弈模型纳什均衡定义如下所示。足下述条件：即对于任一实数对(C，λ)其必须满足下述所示表达式：U()≥ U()，∀i且R(λ*，C*)≥ R(λ，C*)。

3 Stackelberg博弈模型纳什均衡分析

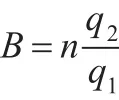
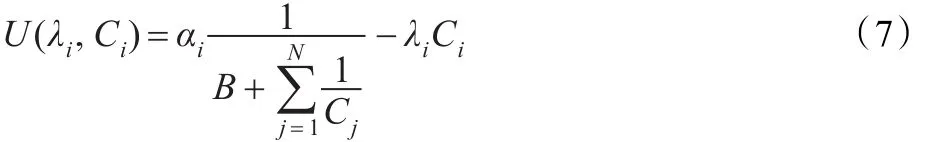
对式（7）求关于Ci的一阶导数可得如下所示的式子：

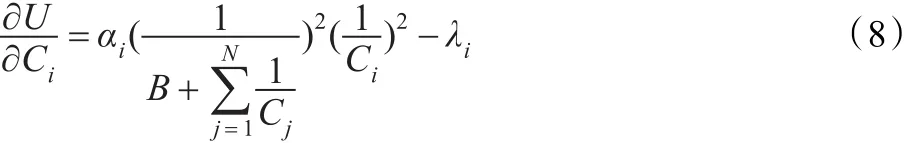
对i=1，2，…，N，变换式（9）并对其进行累加可得下述表达式：

将式（10）代入式（9）可得下述表达式：

对式（7）求关于Ci的二阶导数可得下述表达式：

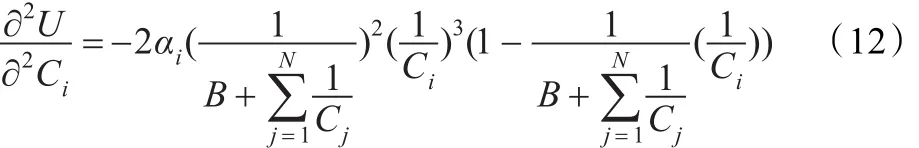
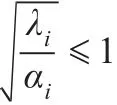
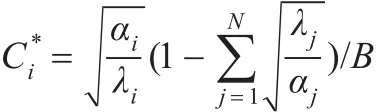
上述引理1表明了认知结点在博弈领头者即无线接入点给定的价格向量基础下，认知结点的最优数据传输速率为所有认知结点价格的函数。由于价格策略是由无线接入点制定的，因此在博弈过程中可以把价格向量看成公共信息，每个认知结点流量可以分布式地根据最优迭代算法来获取其最优数据传输速率即模型的纳什均衡。

对于网络中博弈的领头者无线接入点而言，其通过制定最优价格策略来最大化网络收入即最大化式（6），根据第2章的无线接入点收益模型描述，把式（11）代入式（3）可得博弈领头者的效用表达式如下所示：

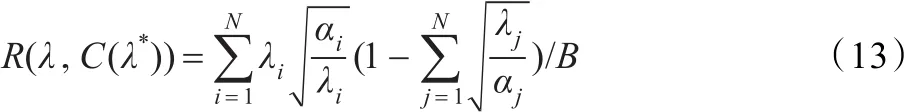
对式（13）求关于λi一阶导数整理可得：

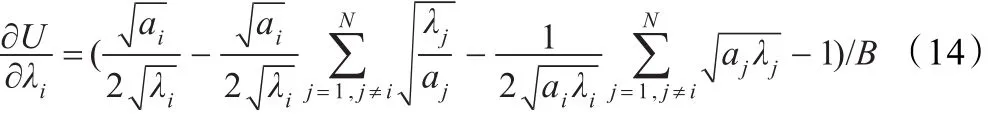
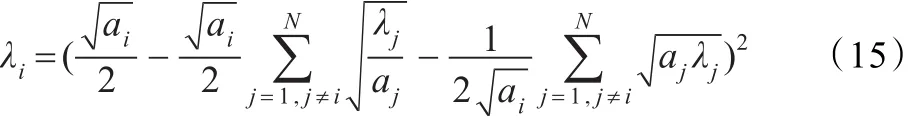
对式（13）求关于λi二阶导数可得表达式如下所示：

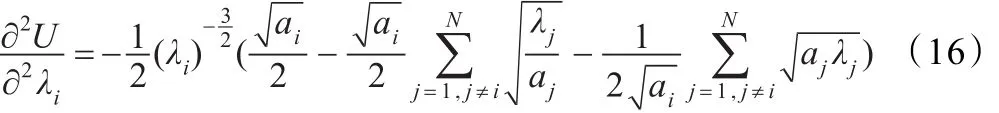
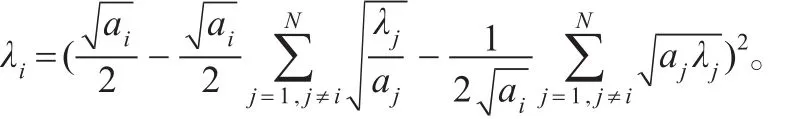
引理2表明通过制定最优价格策略，认知无线单跳网络流量速率控制Stackelberg博弈模型中网络效用存在最优解，在最优解处网络的总体效用（即所有认知结点支付成本之和）是最大的，且认知结点自适应地在认知无线接入点制定的价格基础上最大化自身效用并可得到纳什均衡解。由于网络中存在最优价格向量使得网络效用最大化，而对于任一给定价格向量非合作博弈的认知结点间存在纳什均衡解，根据给出的Stackelberg博弈模型的定义，在给出的引理1和引理2基础上，可以给出认知无线单跳网络Stackelberg博弈模型的纳什均衡解存在性和唯一性定理。

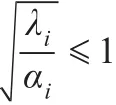
由上述定理可知，提出的认知无线单跳网络速率控制Stackelberg博弈模型纳什均衡是存在的且纳什均衡是唯一的。因此同样地可通过反向归纳法对提出的Stackelberg模型进行纳什均衡求解，算法主要思路是首先对不同结点的加权因子进行赋值，认知接入点通过迭代计算出网络中结点的最优价格向量，结点根据制定的最优价格自适应地计算出最优数据传输速率并返回网络当前的最优效用值，提出流量速率控制模型的纳什均衡求解算法具体如下所示。

流量速率控制模型纳什均衡求解算法：

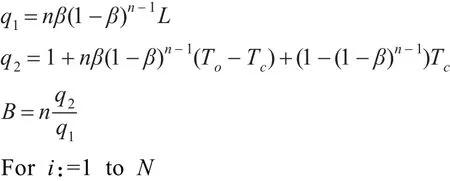
对结点加权因子ai赋值

对结点价格向量λi初始化

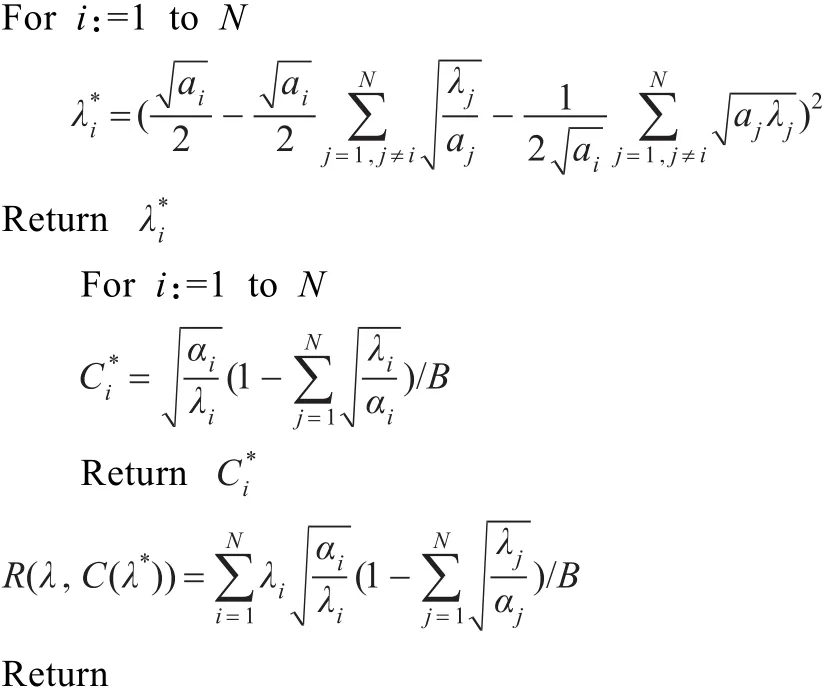
4 数值仿真

本章将通过数值仿真来验证提出的基于Stacklberg博弈的认知无线单跳网络速率控制模型的正确性和有效性。假设网络中的认知结点都是采用基于IEEE 802.11的分布式协调功能进行通信，假设网络中的认知结点使用避退参数都是一致且发送数据包大小都为L，则可用第3章提出的公式计算网络中认知结点的吞吐率，在本章实验中结点吞吐率表达式中的相应参数值设置如下：L=1 500 Byte，b0=16，bk=2kb0，数据帧传输串音 T0=52 slot，RTS冲突串音Tc=17 slot，定义时隙的大小为20 us且K=10，数据传输速率0＜C≤100（单位：MB/s）。不失一般性，可假设认知无线网络中有两个认知结点，且所有认知结点的加权因子αi由结点自身情况决定，认知无线单跳网络的具体示意图如图2所示。

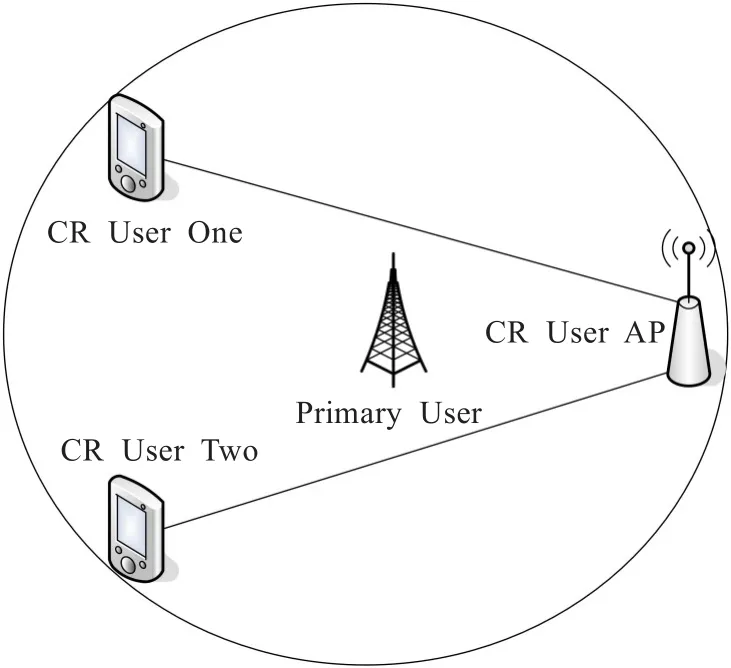
图2 实验网络拓扑图

在第一个实验中假设结点加权因子αi=5，仿真研究提出的Stackelberg博弈模型中认知无线接入点最优收益。图3给出了认知无线单跳网络的效用随认知无线接入点制定价格的变化示意图，从图中可以看出给定相应认知结点的价格向量，网络总是存在着最大效用向量，图中加号绘制的线条即为在不同价格参数下网络最大收益值，图4给出了认知无线单跳网络中在认知接入点制定最优价格向量变化时的结点最优数据传输速率，从图中可以看出由于结点加权因子相等导致结点1最优数据传输速率的下降幅度和结点2最优数据传输速率的上升幅度相似，且其随着价格向量变化趋于稳定。由此可见提出的Stackelberg博弈模型中网络效用存在着最大值，且网络整体效用最大时认知结点可获得最优数据传输速率，从而验证了模型的正确性。

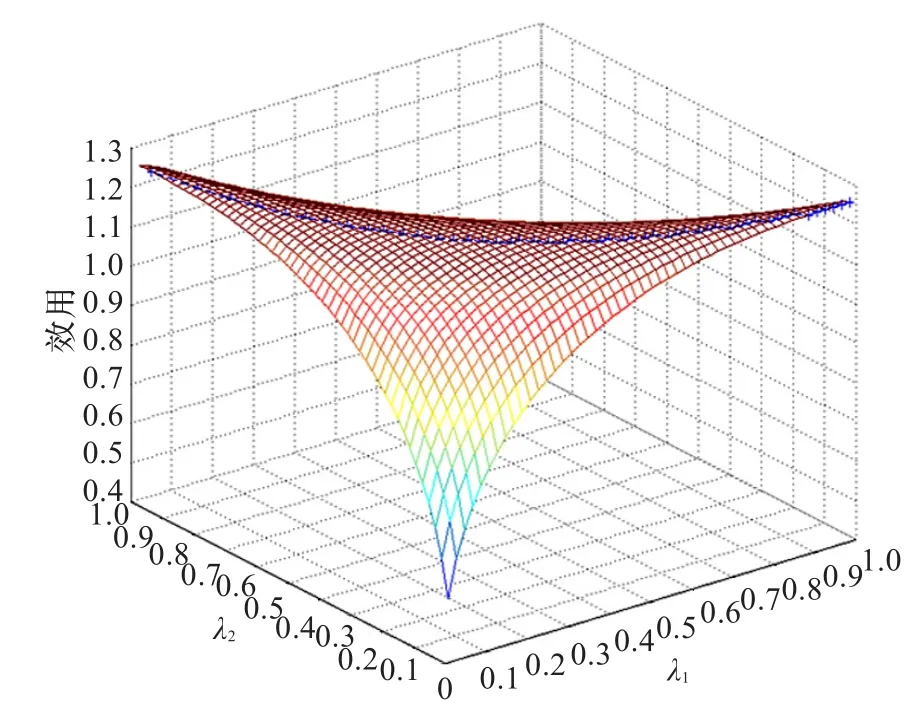
图3 认知无线网络结点加权因子相等时网络收益图

图4 加权因子相等时认知无线网络结点最优数据传输速率示意图

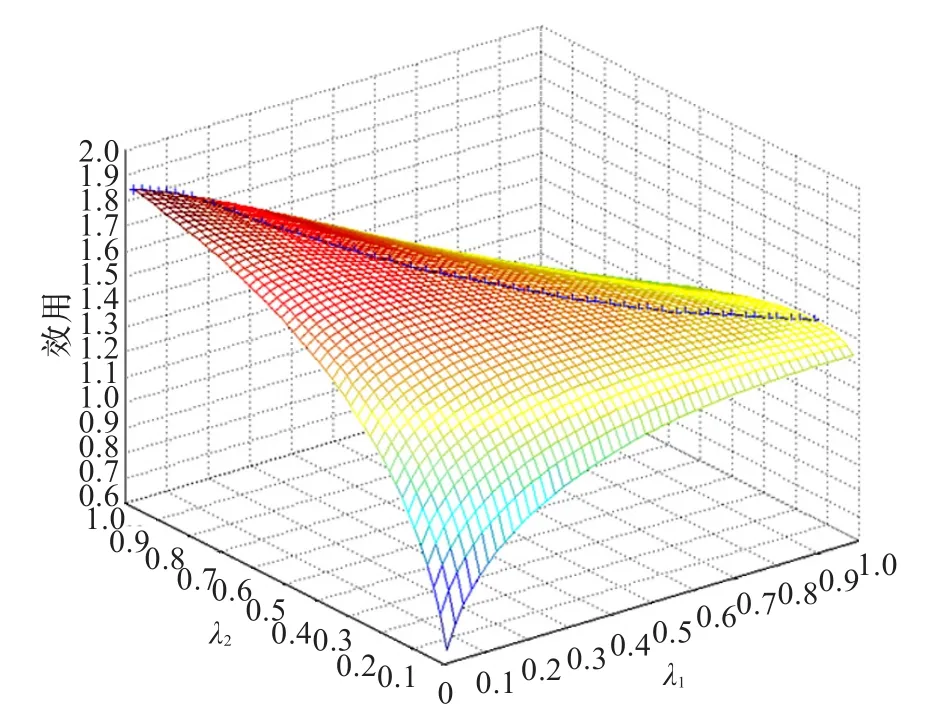
图5 认知无线网络结点加权因子不等时网络收益图

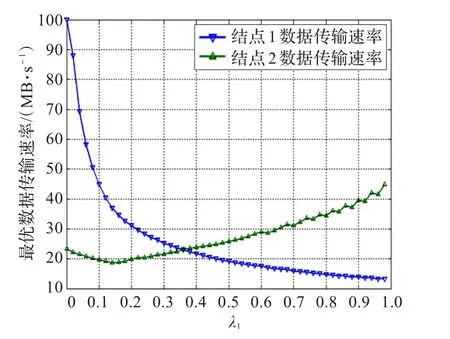
图6 加权因子不等时认知无线网络结点最优数据传输速率示意图

同样地假设认知无线网络中有两个认知结点，与上述不同的是假设认知结点的加权因子αi不相等，在本实验中随机地假设认知结点1加权因子αi=5，认知结点2的加权因子为αi=8。仿真得到的认知无线网络整体收益随认知无线接入点制定价格的变化趋势如图5所示，从图中同样地可以看出给定认知结点相应价格向量，网络存在着最大收益向量，图示中加号绘制的线条即在不同价格参数下网络最大收益值。由于认知结点1的加权因子小于认知结点2加权因子，网络整体收益受认知结点2影响较大，从而导致图中随着价格变化网络收益变化的幅度更大。图6给出了认知无线单跳网络中在认知接入点制定的最优价格向量变化时的结点最优数据传输速率，从图中可以看出由于结

点加权因子不一致导致结点最优数据传输速率的变化幅度也不一致，但其都随着价格向量变化趋于稳定。通过实验表明提出博弈模型的Stacklberg均衡网络效用存在着最大值，且网络整体效用最大时认知结点可获得最优数据传输速率，从而验证了模型的正确性。

5 小结

应用Stackelberg博弈模型研究了认知无线单跳网络流量速率控制问题，在详细介绍Stackelberg博弈模型的基础上，根据基于IEEE 802.11技术的认知无线单跳网络结点速率控制模型，定义认知结点效用函数为流量吞吐率收益减去支付给认知无线接入点的成本，无线接入点效用函数为认知网络中认知结点所付成本总和，给出了流量速率Stackelberg博弈模型的纳什均衡的具体定义，从而建立了基于Stackelberg博弈的认知无线单跳网络流量速率控制模型。应用反向归纳法对提出流量速率Stackelberg博弈模型纳什均衡进行了分析，证明了提出的模型纳什均衡存在性及唯一性。通过仿真验证了提出的模型正确性，仿真结果表明在模型的纳什均衡处网络总体效用是最优的，且网络效用最大时认知结点可获得最优数据传输速率。本文考虑仅是简单的认知无线单跳网络，应用博弈论对基于协作中继的认知无线单跳网络等更为复杂的网络的速率分配及控制问题进行研究将是本文的后续工作。

[1]Im Sooyeol，Jeon Hyoungsuk，Lee Hyuckjae.Autonomous distributed power control for cognitive radio networks[C]//The 68th IEEE Vehicular Technology Conference，Calgary，AB，Canada，2008.

[2]Fudenberg D，Tirole J.Game theory[M].Cambridge，MA：The MIT Press，1991：10-29.

[3]Etkin R，Parekh A，Tse D.Spectrum sharing for unlicensed bands[J].IEEE Journalon Selected Areasin Communications，2007，25（3）：517-528.

[4]Subramani S，Basar T，Armour S，et al.Noncooperative equilibrium solutions for spectrum access in distributed cognitive radio networks[C]//IEEE Symposium on New Frontiers in Dynamic Spectrum Access Networks（DySPAN 2008），Chicago，IL，United States，2008：740-744.

[5]Wang Beibei，Wu Yongle，Liu K J R.Game theory for cognitive radio networks：an overview[J].ComputerNetworks，2010，54（14）：2537-2561.

[6]Liu Mingyan，Ahmad S H A，Wu Yunnan.Congestion games with resource reuse and applications in spectrum sharing[C]// Proceedings of the 2009 International Conference on Game Theory for Networks，Istanbul，Turkey，2009：171-179.

[7]Niyato D，Hossain E.Competitive pricing for spectrum sharing in cognitive radio networks：dynamic game，inefficiency of Nash equilibrium，and collusion[J].IEEE Journal on Selected Areas in Communications，2008，26（1）：192-202.

[8]Del Re E，Gorni G，Ronga L，et al.A power allocation strategy using game theory in cognitive radio networks[C]//Proceedingsofthe2009 InternationalConferenceon Game Theory for Networks，Istanbul，Turkey，2009：117-123.

[9]Wu Yuan，Tsang D H K.Distributed multichannel power allocation algorithm for spectrum sharing cognitive radio networks[C]// IEEE Wireless Communications and Networking Conference，Las Vegas，NV，United States，2008：1436-1441.

[10]Simeone O，Stanojev I，Savazzi S，et al.A stackelberg game for power control and channel allocation in cognitive radio networks[J].IEEE Journal on Selected Areas in Communications，2008，26（1）：203-213.

[11]Lee Jiwoong，Pollin S，Rabaey J M.A revenue enhancing Stackelberg gameforownersin opportunisticspectrum access[C]//New Frontiers in Dynamic Spectrum Access Networks（DySPAN 2008），Chicago，IL，United states，2008：1-8.

[12]Baharlouei A，Jabbari B.A Stackelberg game spectrum sensing schemein cooperativecognitiveradio networks[C]// IEEE WirelessCommunicationsandNetworkingConference（WCNC 2012），Shanghai，China，2012：2215-2219.

[13]Chen Lin，Leneutre J.On the power and rate control in IEEE 802.11 WLANs-a game theoretical approach[J]. IEEE Journal on Selected Areas in Communications，2008，26（7）：1128-1137.

[14]Zhang Jin，Zhang Qian.Stackelberg game for utility-based cooperativecognitiveradio networks[C]//The10th ACM International Symposium on Mobile Ad Hoc Networking and Computing，New Orleans，Louisiana，USA，2009：23-31.

[15]Rosen J B.Existence and uniqueness of equilibrium points for concave N-person games[J].Econometrica，1965，33（3）：520-534.

基于Stackbelberg博弈的认知无线网络速率控制模型

冯慧斌1，翁鲲鹏2，余根坚1

FENG Huibin1,WENG Kunpeng2,YU Genjian1

1.Department of Computer Science,Minjiang University,Fuzhou 350108,China
2.Academy of Communication Technology,Fuchun Communication Corporation,Fuzhou 350003,China

Cognitive wireless single hop network rate control model on Stackelberg game is proposed.By applying the backward induction to analyse the Nash equilibrium,the existence and uniqueness of the proposed model’s Nash equilibrium are proved,and the Nash equilibrium’s specific expression of the Stackelberg game model is given.Simulation validates the correctness of the proposed model,simulation results show the utility is optimal at the Nash equilibrium point,and the cognitive user can achieve the optimal date rate on the Nash equilibrium point.

Stackelberg game;cognitive wireless single hop network;rate control

提出了基于Stackelberg博弈的认知无线单跳网络流量速率控制模型。应用反向归纳法对提出的流量速率Stackelberg博弈模型纳什均衡进行了分析，证明了提出的模型纳什均衡存在性及唯一性，并给出了Stackelberg博弈模型纳什均衡解的具体形式。仿真验证了提出的模型正确性，仿真结果表明在模型的纳什均衡处网络总体效用是最优的，且网络效用最大时认知结点可获得最优数据传输速率。

Stackelberg博弈；认知无线单跳网络；速率控制

A

TP393

10.3778/j.issn.1002-8331.1212-0307

FENG Huibin,WENG Kunpeng,YU Genjian.Cognitive wireless network rate control model on Stackelberg game.Computer Engineering and Applications,2013,49（11）：66-71.

国家自然科学基金（No.61163055）；福建省自然科学基金（No.2011J05155）；富春通信股份有限公司预研项目资助。

冯慧斌（1980—），男，博士，讲师，研究领域为认知无线电网络、无线资源管理；翁鲲鹏（1976—），男，高级工程师，研究领域为无线通信；余根坚（1969—），男，博士，副教授，研究领域为无线通信及信息安全。E-mail：35426918@qq.com

2012-12-26

2013-03-04

1002-8331（2013）11-0066-06