李萨如图形在系统频率特性测量实验中的应用

张海燕，冯蓓娜

（湖南大学 电气与信息工程学院，湖南 长沙 410082）

频率特性分析法是控制理论中常用的系统分析法，具有物理意义明确、计算量小、简单、直观等优点，易于在工程技术界应用，并且可以采用实验方法求出系统或原件的频率特性，易于研究机理复杂或机理不明的系统，也适用于某些非线性系统。有效地利用频率特性曲线而不必求解复杂的解析式，对于无法取得数学模型的复杂对象来说尤为重要[1－2]。然而，由于课本上相关章节的内容抽象、复杂，该部分内容的教学一直是自动控制原理课程教学中的重点和难点，而做好课程实验对帮助学生理解和掌握理论知识及提高动手能力都具重要意义。根据自动控制原理的教学大纲要求，系统频率特性的测量实验是自动化、电气工程、电子、仪器仪表类本科生的必做实验。

控制系统的频率特性反映正弦信号作用下系统响应的性能。由于稳定的控制系统的正弦输出信号与输入信号频率相同，故利用李萨如图形可以测量2个同频率信号的幅值比（幅频特性）和相位差（相频特性）[3－4]，这种方法简单方便，易于掌握和实现。

1 李萨如图形简单介绍

在示波器的Y通道和X通道分别加上不同信号时，示波器屏幕上光点的径迹将由2个信号共同决定，如果这2个信号是正弦波，则屏幕上的图形将取决于不同频率比以及初始相位差而表现为形状不同的图形，这就是李萨如图形[5]。在两信号频率相同的情况下，李萨如图形是简单的封闭曲线。

李萨如图形的大小由2个正弦输入信号的最大振幅决定，形状和光点的运动方向则由相位差决定。当2个信号频率相同且相位差一定时，李萨如图形是唯一的，且与输入信号的初相位无关[6－8]。

根据相位差的不同，李萨如图形的形状和光点运动方向如图1所示[9]（以相位差为特殊情况为例）

根据以上分析，只要测出不同频率点李萨如图形（见图2）所示的xm、ym、x0或y0（xm为输入信号的最大幅值，ym为输出信号的最大幅值，2x0和2y0为椭圆与x轴和y轴交点间的距离），便可计算出系统在各频率点的幅值比和相位差，结合光点的运动方向便可以判断相位的超前滞后情况，进而作出系统的频率特性曲线（曲线绘制方法见文献10）。

图2 李萨如图

2 测量方法举例

一个典型的二阶系统可以用图3的电路图来模拟[11]。

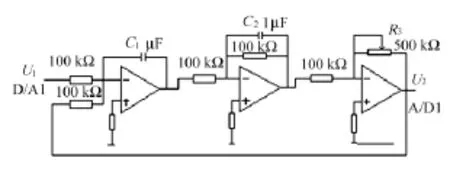
图3 典型二阶系统电路图

具体测量步骤如下：

（1）按图4所示连接电路图；

（2）调节示波器至正常工作状态；

（3）将系统的输入U1和输出U2分别接入示波器的X通道和Y通道；

（4）调节X、Y通道信号，将图形移至示波器荧光屏的中心；

（5）此时荧光屏上显示如图2所示的李萨如图形，测出xm、ym、x0或y0；

（6）保持输入信号幅值不变，改变输入频率，观察李萨如图形的变化，测量对应xm、ym、x0或y0；

（7）计算幅频特性和相频特性；

（8）根据计算值绘制频率特性曲线。

其中，根据幅频特性的定义，幅频特性的计算公式应为L（ω）＝ym／xm，因为在实验过程中一直保持输入信号的幅值不变，所以xm只需测量1次即可。

相频特性的计算公式推导如下：

若控制系统的输入信号（接示波器x轴）为

控制系统的输出信号（接y轴）为

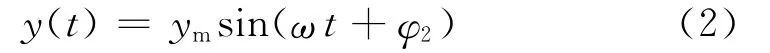
则有：

用式（3）或式（4）计算所得的相频特性与理论上应该是一样的，因为实验过程中xm始终保持不变，所以用式（4）计算可以减少工作量，提高精度。

上式适用于椭圆长轴在一三象限，若椭圆长轴在二四象限时，计算公式变为：

上述相频特性计算公式推导过程中，是默认了y轴信号超前x轴信号的情况。应当指出，实际的系统中一般输出是滞后于输入的[12]，若用上述公式进行计算，则计算结果应加负号。现就不同情况下的相频特性计算公式等列于表1。

表1 不同情况下相频特性

3 结束语

李萨如图形法测量系统频率特性简单、直观，方便易行，不仅有助于学生理解和掌握课堂内容，也为以后从事相关研究工作打下基础。但测量精度不高，且受输入频率影响较大，当频率较高时，光点的运动方向不易看出，只能靠测量数据的连续行来估算相频特性的正负号。另外，当2个信号的相位差接近于0或π时，李萨如图形接近直线，此时测量误差较大。所以实验时，选取合适的频率点对测量精度有较大影响。

（References）

[1] 梅晓蓉.自动控制原理[M].北京：科学出版社，2007.

[2] 胡寿松.自动控制原理[M].北京：科学出版社，2007.

[3] 管莉.李沙育图形在测量中的意义[J].郑州铁路技术职业学院学报，2004，16（1）：55－56.

[4] 王靖.电子示波器对两个同频正弦信号相位差的两种测量方法的对比分析[J].黔西南民族师范高等专科学校学报，2010（1）：110－112.

[5] 张永瑞.电子测量技术基础[M].西安：西安电子科技大学出版社，2009.

[6] 张伟刚，陆晓.相互垂直简谐振动合成规律CAI演示软件[J].广西工学院学报，1995，6（3）：48－52.

[7] 杨继先.李萨如图形的性质研究[J].西华大学学报：自然科学版，2008，27（6）：98－100.

[8] 赵波.关于李萨如图形讨论的小结[J].大学物理，1997，16（11）：19－21.

[9] 宋明秋.李萨如图形及其应用[J].辽宁师专学报，2010，12（1）：23－86.

[10] 谷雷.绘制系统开环对数频率特性曲线的教学方法与技巧[J].科技信息，2011（35）：453－454.

[11] 北京精仪达盛科技有限公司.自动控制理论实验指导书[M].2版.北京精仪达盛科技有限公司.

[12] 张玉莲，宋双杰.李萨如图形在检测系统中的应用[J].力学与实践，2006，28（5）：54－57.