盲小波算法在金属矿床地震资料去噪处理中的应用

周仲礼，秦飞龙，夏欢欢，苏建美

（成都理工大学 数学地质四川省重点实验室，成都610059）

与油气的地震资料相比，金属矿床地震资料的噪声干扰更强，传统的去噪方法很难有效地处理金属矿床的地震资料。小波阈值去噪［1，2］是处理地震资料的重要方法，它只能消去高频噪声或者随机噪声，对相干噪声的处理能力十分有限；但是信号通过小波分解之后能把时间域的信号转换到时频上，使信号更为精细［3，4］。目前刚刚兴起的基于多通道盲源分离技术［5－9］在地震资料处理上取得了一些应用，能得到所需要有用信号和去掉部分与源信号无关的信息，但事实上盲分离技术的降噪效果还是不理想。因为盲信号分离的前提是要求观测到的信号是由源信号线性混合而成的，事实上通过检波器观测到的地震信号是源信号和噪声做卷积之后的结果，没有完全满足盲信号分离的假设条件。因此有必要深入研究盲信号和小波分析，克服两者的缺点，充分发挥出它们优势，构造出新的去噪算法以便对低信噪比的金属矿床地震资料进行去噪。

1 盲小波算法

1.1 盲信号分离去噪与小波阈值去噪的优缺点

在地震资料中，当源信号和噪声是相互独立并且是瞬时线性混合时，那么在不知道各种信号的先验知识情况下，通过盲信号分离算法对观测到的信号进行盲分离就能得到各种信号。然而通过检波器收集到的地震信号是噪声与源信号做卷积之后的结果，不满足盲信号分离的假设条件。小波分析是“信号显微镜”，信号通过小波分解之后能观测到信号不同频率带的细节信息，随机噪声是属于高频信号的，通过阈值法就能除去随机噪声。对于线性噪声等相干噪声小波阈值去噪法就很难实现。但是信号经过小波分解到不同频率带之后，信号变得更加精细，更利于处理，通过小波重构能还原信号。事实上，小波分解就是一个解卷积的过程，把信号分解到不同的频率带上，重构的过程就是一个做卷积的过程。

1.2 盲小波算法提出

对地震记录进行分频去噪是目前地震信号去噪的一个主要研究方向。由于地震记录的不同频率成分有不同的信噪比，对不同频带的信号进行去噪更加科学。根据小波分析的相关理论可知，信号经过小波变换之后，信号分解到不同的尺度空间上，并且其频率带也不相同，与尺度空间是一一对应的关系。可以这样认为：原信号是经过小波变换到不同尺度空间下的所有的信号的一种叠加，不同尺度空间上信号的细节方面更为清晰，更利于处理。本文根据该想法提出了一种新的消除地震信号噪声的算法——盲小波算法：首先将一组相邻的观测信号分解到不同的尺度空间上，利用阈值法对相应尺度空间下的小波系数进行处理；然后在不同尺度空间下对信号进行盲信号分离，分离出对应尺度空间下的源信号；最后根据小波逆变换把尺度空间下的信号重构为源信号。在小波分析这个信号显微镜下，这样做不但满足了盲分离的条件，也满足了分频去噪的要求。

2 一维盲小波算法原理

2.1 盲小波算法的设计

在金属矿床地震资料中原始地震资料信息受到的干扰较大，有大量的随机噪声、相干噪声以及干扰噪声等，严重影响了地震资料的本质信息。随机噪声主要存在于高频部分，相干噪声出现在不同频率带上。观察到的信号是经过褶积之后的结果，小波分解就近似于解褶积的过程，同时将信号分解到不同的频带上，满足了盲源分离要求信号是线性的条件。因此，可以构造出新的降噪方法如图1所示。用小波变换将原始地震信号中相邻的几个信号分解到不相同的尺度空间上，然后利用小波阈值法处理尺度空间上的小波系数，再对相同尺度空间上的地震信号进行盲信号分离，提取出有效的地震信号。最后通过小波逆变换将所有尺度空间上的信号重构为源信号。经过这种新的变换之后，能够有效除去地震信号中的干扰波，从而达到去噪的目的。

2.2 盲小波算法流程

对一组相邻的原始地震信号f＝ （f1，f2，…，fn）做如下处理。

a.由采样定理知，将信号f1，f2，…，fn做2j尺度空间上的近似采样，得到fj1，fj2，…，fjn。利用合适的小波基来对采样之后的信号进行N次小波分解，即

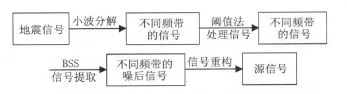
图1 盲小波算法的思想描述Fig.1 Thought description block diagram of blind wavelet algorithm

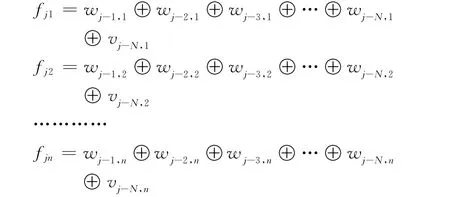
其中wj－h，k（h＝1，2，…，N）表示fjk在2j－m尺度空间下细节信号，vj－N，h表示信号fjk在2j－N尺度空间下的尺度信号。

b.对所有的不同频带的小波系数进行软阈值法处理。

根据小波的软阈值处理法，对 wj－i，1，wj－i，2，…，wj－i，n（i＝1，2，…，N）里面的所有系数进行软阈值法处理，得到新的估计信号

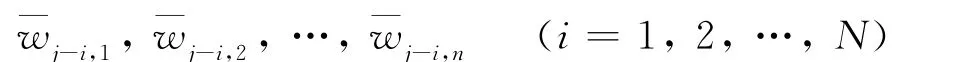
c.对不同信号的同尺度上的信号进行盲源分离得到有效地震信号。

然后对vj－N，1，vj－N，2，…，vj－N，n（i＝ 1，2，…，N）进行盲分离，提取出有效地震信号

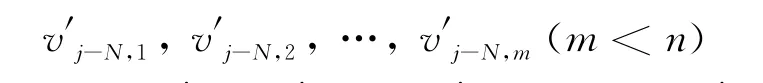
于是有f′ji＝w′j－1，i⊕w′j－2，i⊕ … ⊕w′j－N，i⊕v′j－N，i（i＝1，2，…，m）

d.利用 Mallat算法［10］将信号w′j－1，i，w′j－2，i，…，w′j－N，i，v′j－N进行重构为f′ji，其中（i＝1，2，…，m）。盲小波算法流程图如图2所示。

2.3 盲小波算法的参数选取

盲小波算法的实现是需要参数的，参数的类型如下。

图2 盲小波算法的流程图Fig.2 The flow chart of one－dimensional blind wavelet algorithm

a.适当的小波基，例如db系列小波、sym系列小波。对于地震资料一般选取的小波基是sym系列小波，具体选取哪类小波，要对信号做小波分解和重构之后确定。

b.小波分解的层数，一般而言，一维小波分解的层数是3～6层。

c.阈值选取，处理不同频带的小波系数选取的阈值是有区别的，也就是将信号分解多少层就需要选取多少个阈值系数。对所有的小波系数采取同样的阈值，出现的结果是，有些频带的小波系数损失过重，还有些频带的小波系数没有得到有效压制。

d.盲信号分离算法的选取。目前比较成熟的算法有 JADE 算 法［11］、FastICA 算 法［13，14］，本 文采用的盲信号分离算法是JADE算法。

3 盲小波算法对实际资料的去噪处理与分析

金属矿床地震数据来源于中国地质调查局地质调查计划项目“深部找矿复电阻率法技术研究”。采样点为6000，采样间隔为1ms，共584道信号。通过对原始地震资料（图3）观察发现，该资料信噪比很低，主要有面波、线性噪声、大量的随机干扰噪声，品质较差，整个资料剖面几乎没有双曲线形态特征，纹理不明显。通过盲小波算法对原始的地震资料处理之后得到的剖面（图4）；通过直接用盲信号分离算法处理得到地震资料的剖面（图5）；通过小波阈值法处理得到地震资料剖面（图6）。

为了能更清楚地了解盲小波算法去掉了哪些噪声，除了得到去噪的剖面之外，还需要了解其噪声的分布特征，以验证盲小波算法的去噪效果。利用获取噪声的算法对原始地震资料进行处理之后得到的噪声分布剖面（图7）。

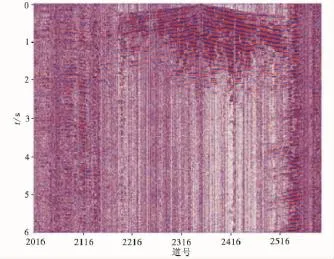
图3 原始地震资料剖面图Fig.3 The original seismic data profile

图4 盲信号分离去噪的剖面图（JADE算法）Fig.4 Blind signal separation de－noising profile（JADE algorithm）

从噪声剖面中可以看出，通过选取适当的参数，去掉的噪声除了随机噪声之外还有面波、线性噪声、声波等相干噪声。从盲小波算法去噪后的地震资料剖面图可知，大量的随机噪声、相干噪声（如线性噪声）等得到了有效的压制，其去噪的效果明显优于直接用盲信号分离去噪和直接用小波阈值去噪。

图5 小波阈值去噪的剖面图Fig.5 Profile after wavelet threshold de－noising

图6 盲小波算法去噪后的剖面Fig.6 Profile after the blind waveletalgorithm de－noising

图7 噪声分布剖面图Fig.7 Noise profile

用小波阈值去噪法处理原始的地震资料得到的数据资料（图6），其效果较原始资料有了部分提高，纹理变清晰了一些，但仍然比较模糊。通过盲信号分离去噪后得到的数据资料（图5），较原始资料的效果有了很大的提高，但仍然有明显的随机噪声干扰。利用盲小波去噪技术对原始地震资料处理，得到的数据资料（图4），不难发现处理后的资料纹理清晰可见，噪声干扰几乎很少，不仅消去了高频噪声，线性噪声也被有效地压制了，使得去噪后的金属矿床地震资料剖面更为流畅清晰，同时具有连续性，有利于以后地震资料解释。

4 结论分析

本文将小波阈值去噪与盲信号分离去噪进行有机结合，将两者扬长避短，构造了处理一维信号的盲小波算法对某金属矿区单炮地震资料进行了处理，得到了相应的去噪剖面与噪声剖面。结果表明盲小波算法去噪优势明显，能有效地消去资料的随机噪声、线性噪声、面波、声波等噪声干扰，使得去噪后的地震资料双曲线特征表现得比较明显、地震剖面更加清晰流畅，信噪比变高，满足了资料的高分辨率、高保真度的要求。盲小波算法的一个很重要的假设是源信号至多一个是非高斯性的，并且要求源信号是相互独立的，否则算法失效（或者部分失效）。在实际情况下随机噪声一般是高斯性的，但经过小波阈值处理之后，随机噪声的影响几乎没有，在使用盲信号提取信号时就不需要考虑其噪声的高斯性了。但一维盲小波算法是处理2道相邻地震信号，对多通道地震信号处理将是今后研究的课题。

［1］赵天娇，何选森，陈利.基于新阈值函数小波变换的噪声盲分离算法［J］.计算机应用研究，2010，27（8）：2886－2888.Zhao T J，He X S，Chen L.Noisy blind source separation algorithm based on new threshold function of wavelet transform［J］.Application Research of Computers，2010，27（8）：2886－2888.（In Chinese）

［2］Li J，Cheng C K，Jiang T Y.Wavelet de－noising of partial discharge signals based on genetic adaptive threshold estimation［J］.IEEE Transactions on Dielectrics and Electrical Insulation，2012，19（2）：543－548.

［3］Liua C C，Sun T Y.Heuristic wavelet shrinkage for denoising［J］.Applied Soft Computing，2011，11：256－264.

［4］Zhang H，Blackburn T R，Phung B T，et al.A novel wavelet transform technique for on－line partial discharge measurements：1.WT denoising algorithm［J］.IEEE Trans Dielectr Electr Insul，2007，14（4）：3－14.

［5］Cardoso J F，Souloumiac A.Blind beamforming from non－Gaussian signals［J］.Proc Inst Elect Eng－F，1993，140（6）：362－370.

［6］史习智.盲信号处理：理论与实践［M］.上海：上海交通大学出版社，2008：47－72.Shi X Z.Blind Signal Processing：Theory and Practice［M］.Shanghai：Shanghai Jiaotong University Press，2008：47－72.（In Chinese）

［7］Cichocki S A.自适应盲信号与图象处理［M］.北京：电子工业出版社，2005：630－664.Cichocki S A.Adaptive Blind Signal and Image Processing［M］.Beijing：Electronic Industry Press，2005：630－664.（In Chinese）

［8］李加文，李从心.基于频域盲解卷的噪声信号分离［J］.振动与冲击，2006，25（6）：100－107.Li J W，Li C X.Noise seperation based on blind deconvolution in prequency domain［J］.Journal of Vibration and Shock，2006，25（6）：100－107.（In Chinese）

［9］Cichocki，Amari S I.Adaptive Signal and Image Processing：Learning Algorithms and Applications［M］.New York：Wiley，2002.

［10］Cardoso J F.Souloumiac A.Blind beamforming for non－Gaussian signals［J］.IEEE Proceedings F，1993，140（6）：362－370.

［11］Cardoso J F.High－order for independent component analysis［J］.Neural Computation，1999，342（1）：157－192.

［12］Zbynek Koldovsky.Efficient variant of algorithm FastICA for independent component analysis attaining the cramer－Rao lower bound［J］.IEEE Transactions on Neural Networks，2006，17（5）：1265－1276.

［13］张念，刘天佑，李杰.FastICA算法及其在地震信号去噪中的应用［J］.计算机应用研究，2009，26（4）：1432－1434.Zhang N，Liu T Y，Li J.FastICA algorithm and its application in seismic signal noise elimination［J］.Application Research of Computers，2009，26（4）：1432－1434.（In Chinese）