长距离带式输送机驱动装置动力学特性的研究
2013-08-01刘云峰
马 涛,韩 刚,刘云峰
(太原科技大学机械工程学院,太原030024)
带式输送机驱动系统[1]主要由驱动电机、联轴装置、减速器及相关的控制系统等组成,系统简图如图1所示。
带式输送机的驱动电机可采用鼠笼式交流电动机、绕线式交流电动机和直流电动机。直流电动机调速范围广,过载、启动、制动力矩大、可靠性高,但是它的明显缺点是造价高,维护量大,所以目前多数采用结构简单、价格低廉效率高的交流异步电动机。
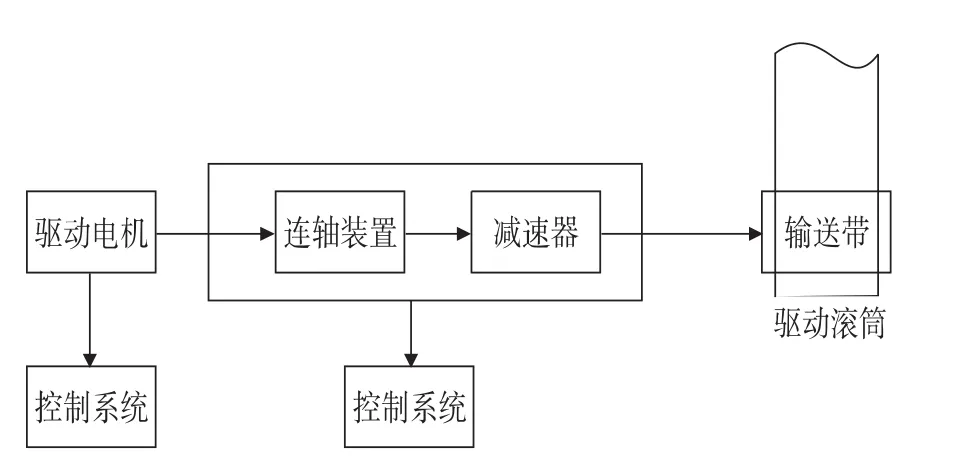
图1 带式输送机驱动系统模型简图Fig.1 The model diagram of belt conveyer driving system
联轴装置用于连接电机与减速器(有些驱动装置中联轴器与减速器为一体结构),可以进一步调整改善电动机的输出特性,使其输出的动力特性更有利于输送机的启制动要求。目前带式输送机上主要采用的联轴装置有联轴器和液力耦合器(限矩型或调速型)、BOSS传动装置、CST传动装置等其它液力传动机构。与电机一样,联轴装置也可以通过增加控制系统调整其特性参数,以满足工作装置对动力输入的不同需求。
齿轮减速器是带式输送机中的常用减速器,其动力特性对输送带的动态响应影响很小,可以忽略,因为齿轮啮合过程中的振动频率远高于输送带,传动滚筒的大惯性质量也能很好的削弱齿轮振动带来的输入动力波动。
1 电动机的数学模型
1.1 鼠笼电动机
鼠笼交流异步电动机在小、中型带式输送机上得到了广泛的应用,而在大型带式输送机上,鼠笼电动机启动力矩不足,启动电流过大,很少单独使用,常与其它驱动系统单元配合使用,下面对它的机械特性进行讨论。
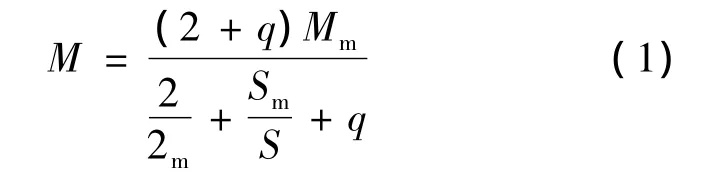
式中:M——电动机输出转矩,N·m;
Mm——电动机输出的最大转矩,Nm;
S——电动机的转差率;
Sm——电动机在最大输出转矩工况下的转差率;
q——与电动机定子转子电阻有关的常数。
从式(1)可看出:只要确定出电动机的最大输出转矩,最大输出转矩工况下的转差率,与电动机定子转子电阻有关的常数就可以确定电动机的机械特性,其中电动机的最大输出转矩可由电动机的额定转矩和过负荷系数得到,因而只需在已知机械特性曲线的两个特殊点即可计算出Sm和q.这两个特殊点是电动机的堵转工况和额定工况。因此可以解出Sm和q.
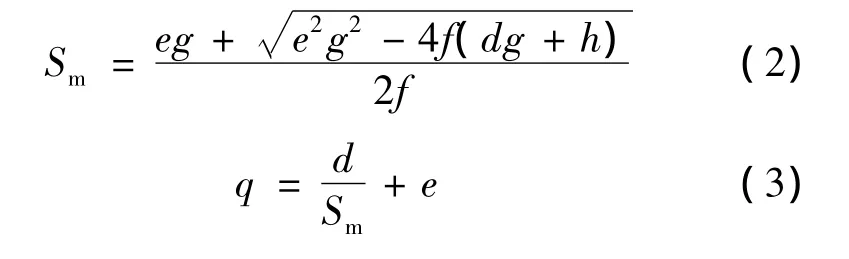
式中:Se——额定转差率:
λ——过负荷系数;
α——堵转力矩系数;
n0——电动机同步转速,r/min;
ne——电动机额定转速,r/min;
电动机最大输出力矩为:Mm=λMe;
式中:Pe——电动机的额定功率,kW.
将式(2)、式(3)代入式(1)即得出电动机的M-n(转矩-转速)特性曲线;
例:对Y450-46-6型电机,给定电动机的额定功率Pe=400 kW;过负荷系数λ=2.57;堵转力矩系数α=1.17;电动机同步转速n0=1 000 r/min;电动机额定转速ne=988 r/min.
由式(1)、式(2)、式(3)绘出电动机特性曲线(如图2)。
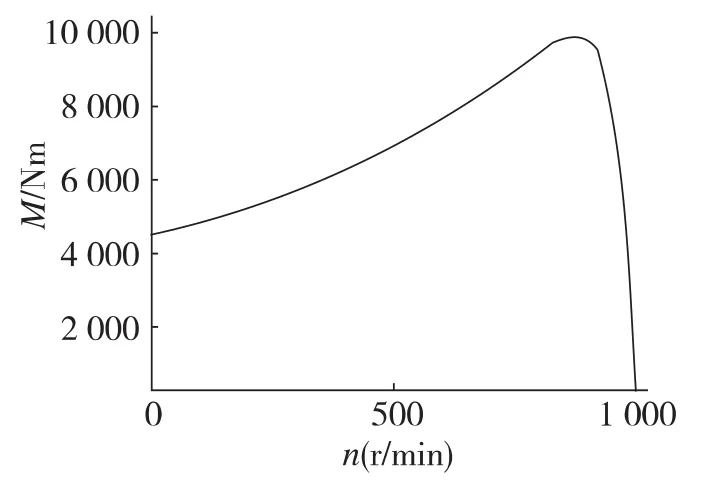
图2 电动机特性曲线Fig.2 The characteristic curve of motor
1.2 绕线电动机
绕线电动机常用转子串接电阻来改善起制动性能,所以它在大中型带式输送机上得到了广泛的应用,由于串电阻的原因,它的特性曲线可以预先设定,启动过程可以人为控制。由电动机机械特性的参数表达法[3],可得绕线式电动机的机械特性为:
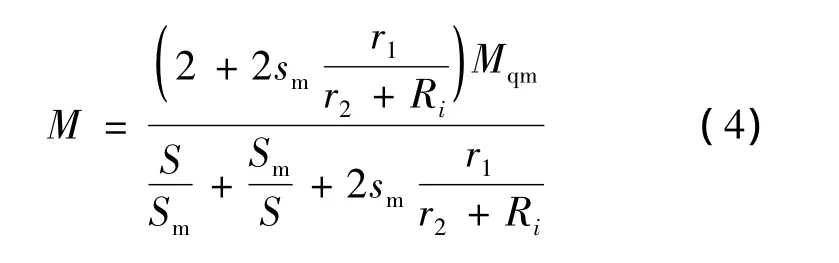
式中:r1、r2—— 定子、转子电路电阻值;
Ri——转子电路串联电阻值。
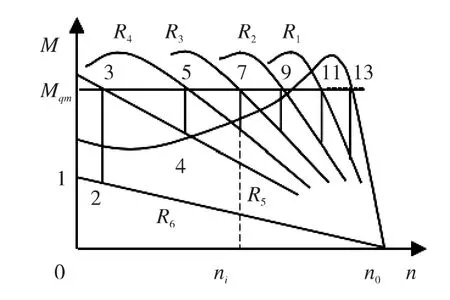
图3 电动机串电阻启动的机械特性[2]Fig.3 Starting mechanical properties of series resistance of motor
绕线电动机的机械特性曲线如图3所示。当切去第i级电阻时,转矩与转速的关系为:
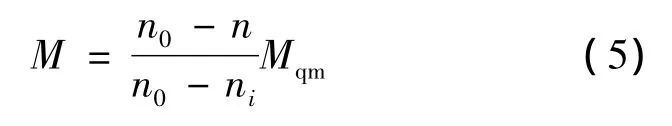
式中:ni——串第i级电阻时,特性曲线上输出转矩为Mqm时的电动机转速,也是切换到第i级电阻瞬间ti(i=1,2,3,4,5,6)时的电机转速;
Mqm——预设的最大启动转矩。
当应用式(5)计算电动机输出转矩时,输出转矩将与电动机的转速有关。对于多自由度的输送机系统,依次建立起来的动力学方程将具有“阻尼力”的耦合,这对求解是不利的[2]。为避免这个问题,作为一阶近似,可按刚体动力学的方法,将电动机输出转矩转换为只与时间有关的函数[3]。设J为驱动系统的总转动惯量,常数Mf为系统运动总阻力矩,根据[4]有
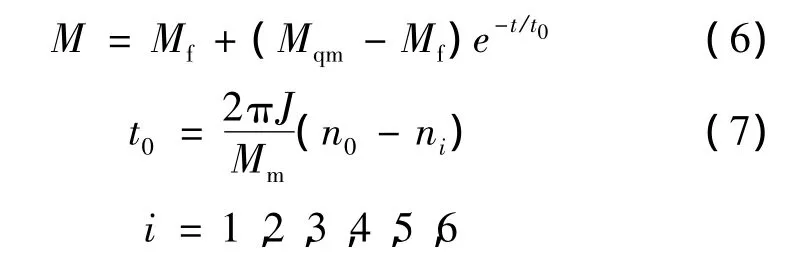
式中:t0——系统时间常数,在不同的特性曲线上数值是不同的。
2 联轴装置的数学模型
联轴装置的作用是传递力矩(电机输出轴到减速器输入轴),并在传递力矩的过程中改变力矩的输出特性。带式输送机的启动装置大多采用一些可以软化启动的联轴装置。联轴装置的类型主要有联轴器、液力耦合器及一些电液控制的联轴系统。
2.1 联轴器的数学模型
带式输送机驱动装置中采用的联轴器可分为刚性和弹性两种。
刚性联轴器是将电机输出轴与减速器输入轴刚性的连接,电机输出转矩直接加载到驱动滚筒上,所以启动特性比较硬,现在已很少使用。
弹性联轴器可以实现电机输出轴与减速器输入轴之间的弹性连接,常用的是弹性柱销联轴器,传递转矩的特性方程为:
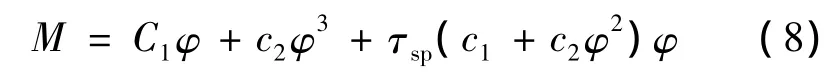
式中:φ——两个半联轴器之间的相对转角;
τsp——反映联轴器弹性元件阻尼特性的滞后时间常数;
c1,c2—— 常系数。
2.2 液力耦合器的数学模型
在耦合器工作过程中,泵轮和涡轮的转矩总有:MT=MB
而有模型试验得到的液力偶合器的流体运动计算方程为:
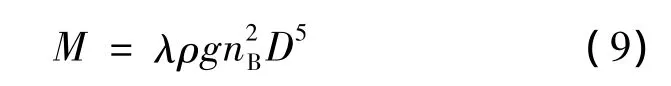
式中:D——液力偶合器的有效直径,m;
nB—— 泵轮转速,r/min;
ρ——工作液体的密度,kg/m3;
λ—— 泵轮力矩系数,min2/(m·r).
力矩系数λ是速比i的函数,即λ=f(i).它与工作轮断面的几何形状、充液量、叶片数、流道光滑度等因素有关。图4为TVA型液力耦合器在不同充液率下的原始特性曲线,从式(9)可以看出,当其他参数一定时,力矩和泵轮的转速的平方成正比。即
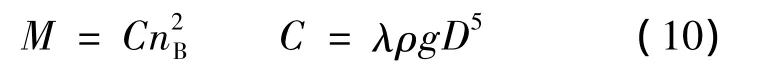
这就是液力耦合器的数学模型。液力耦合器的原始特性曲线、输入特性曲线和输出特性曲线是生产厂家可以给出的,但在实际运行过程中,特别是启动过程,泵轮转速nB要受原动机的影响,是变化的,这样泵轮和涡轮的转速比也是不断变化的,所以其输出特性无法从已知的三条曲线中直接得到。因此对于带式输送机的动态分析,需要把电动机和液力耦合器作为一个整体进行分析来建立驱动系统数学模型,才能得到输送机动力学模型的正确输入特性,才能更加真实的模拟输送机的动态响应。
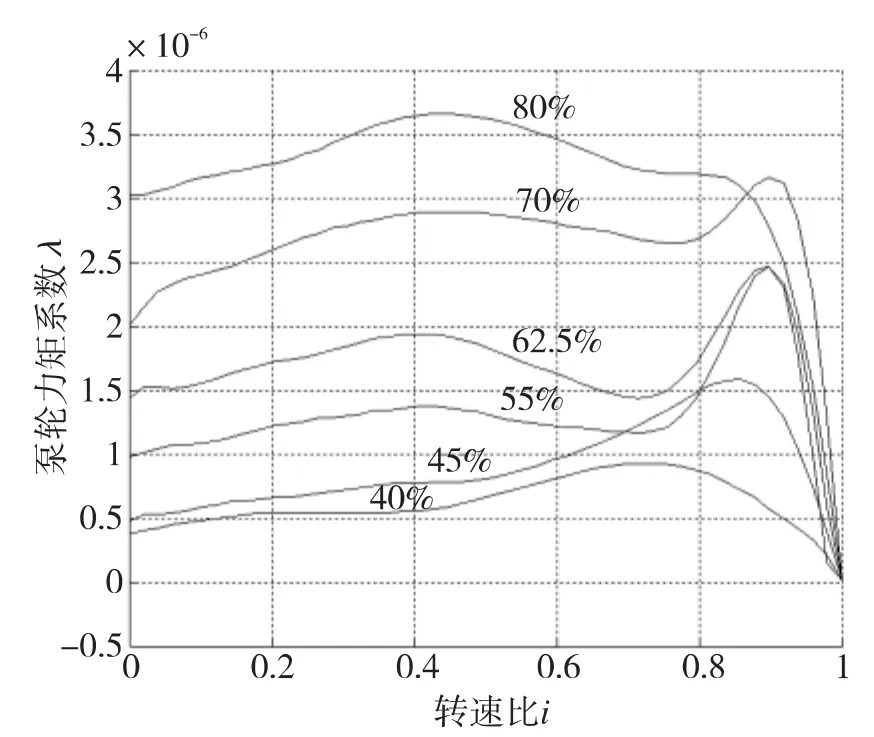
图4 TVA型液力耦合器原始特性曲线Fig.4 The original curve of TVA-type hydraulic couplers
3 电机和液力耦合器联合运行的数学模型
由于输送带的粘弹性特性,在输送机启动时,整条输送带不会同时开始运动,而是逐段启动的。因此在一开始负载力矩较小,随着张力的传播,输送带的逐渐张紧,参与运动的输送带段的增长,负载力矩逐渐增大,直至输送带全部启动并达到额定速度;此时,输送机才进入正常运行状态,负载力矩趋于恒定。如图5所示,在启动过程中,折合到液力耦合器输出轴上的负载力矩沿曲线2变化。
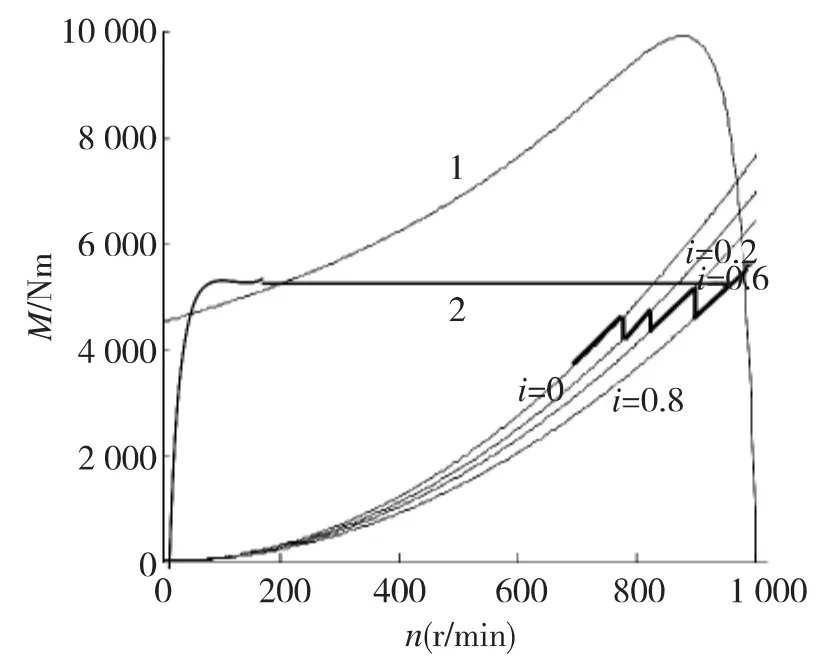
图5 电机和液力耦合器联合启动过程示意图Fig.5 The joint boot process diagram of motor and hydraulic coupler
输送机的启动过程为[5]:电机起动后,转速很低,其输出转矩(即泵轮输入转矩)随转速的增大沿电机的外特性曲线1上升;此时涡轮还没有转动,与电机轴相连的液力耦合器泵轮转矩和转速沿着输入特性曲线i=0上升。电机轴与泵轮的力矩差为泵轮的加速力矩。当泵轮转矩大于负载的起动转矩时,涡轮开始转动,输送机起动,i逐渐增大,这时涡轮的输出转矩沿着新的输入特性曲线变化。随涡轮转速不断增加,涡轮力矩(即泵论力矩)沿液力偶合器输入特性成锯齿形状加大,一直到额定负载转矩和电机输出转矩相等时达到平衡状态,图5为启动过程示意图。
上面是对电动机和液力耦合器联合启动过程的分析,但在模拟仿真输送机的启动过程时,仅分析是不够的,必须要有具体的联合启动输出特性曲线,并能够加载到输送机的动力学模型[6]中去。下面以具体的例子来探讨下求得联合输出特性曲线的过程。当泵轮和涡轮转速比恒定时,有
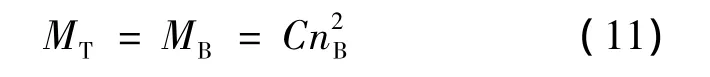
由液力偶合器的原始特性曲线,可计算出相应转速比的C值,再通过式(1)和(11)可求出相应转速比的泵轮转速nB值,通过转速比进一步求得涡轮nT值,这样可以算得某一转速比下的涡轮转矩MT和涡轮转速nT值,依次求出一系列转速比下的MT和nT值。为便于计算机模拟,可通过多项式拟合得到电动机和偶合器的联合工作特性曲线的近似函数表达式,也可通过分段函数曲线来代替联合工作特性曲线,本文采用了前者。其中Ci为相应泵轮和涡轮不同转速比的C值。做法:将式(1)和式(11)联立,得方程:
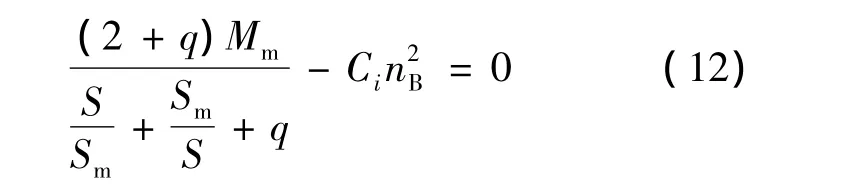
由此得到得到一系列转速比下的(MT,nT),用多项式拟合得到联合工作特性曲线及近似函数表达式。以上面的Y450-46-6型电机和TVA866限距型液力偶合器(充液率为62.5%)为例,绘制的联合特性曲线如图6所示。
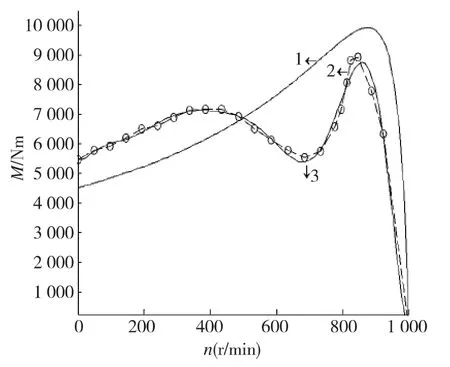
图6 电动机和液力耦合器的联合工作特性曲线Fig.6 The co-operating characteristics curve of motor and hydraulic couplers
4 结论
由以上分析可看出,在驱动装置上配置液力耦合器避免了力矩从电机到输送机上的直接加载,实现了力矩在输送带上的缓慢加载,大大降低了输送带的最大张力[7],减轻了张力冲击与波动。
对于不同的电机输出特性和液力耦合器原始特性,两者的匹配输出特性是有很大不同的。为使驱动系统有个理想的工作状态,必须进行细致的仿真计算与合理匹配,找出液力耦合器与电机的最优组合,使它们的匹配输出特性曲线按需要的形状变化。
[1]宋伟刚.散状物料带式输送机设计[M].沈阳:东北大学出版社,2000.
[2]李光布.带式输送机动态特性研究[D].上海:上海交通大学,2003.
[3]顾绳谷.电机及拖动基础(下)[M].北京:北京机械工业出版社,1981.
[4]胡宗武,乐晓斌.机械结构概率设计[M].上海:上海交通大学出版社,1995.
[5]侯友夫.带式输送机动态特性及控制策略研究[D].徐州:中国矿业大学,2001.
[6]牛巍巍.带式输送机的动态分析研究[D].太原:太原科技大学,2010:7.
[7]邓春芳,王鹰.输送带的张力计算[J].太原重型机械学院学报,2004,25(3):216-218.
