参数变化对简支斜板屈曲承载力的影响规律*

付为刚 程文明 濮德璋 郑严

(西南交通大学机械工程研究所，四川成都610031)

为减轻起重机箱梁结构自重，以树叶叶脉为仿生对象，提出了起重机叶脉斜向肋箱梁结构．起重机箱梁结构通常承受较大的外界压力，斜板的局部失稳容易引起结构整体性破坏．箱梁中的局部斜板可视为简支斜板，因此，针对简支斜板屈曲承载能力的研究对于起重机箱梁结构轻量化设计至关重要．

以往关于弹性板屈曲分析主要采用有限样条法、伽辽金法、里兹能量法等．Lotfi等［1］运用等参样条有限条法研究了楔形板的屈曲问题．陈炎等［2］利用双重Fourier级数展开和Galerkin方法获得单向轴压和简支边界条件下压电矩形薄板后屈曲问题的解析解．Ganapathi等［3］运用有限元法分析了四边简支功能梯度斜板沿厚度方向(非)线性温度变化的热屈曲行为．Xiang等［4］运用里兹能量法分析了四边固支和悬臂等边界条件下，受剪应力作用斜板屈曲临界载荷无量纲值(以下简称屈曲临界载荷)的影响参数，但没有考虑四边简支斜板屈曲临界应力的影响因素，且参数选取范围有限．

微分求积法因具有高精度、高准确性等特点，被用于弹性薄板结构力学分析中［5－6］．Wang 等［7］采用边界融入法(Build－in Method)［8］给出了线性非均布载荷作用下，矩形板屈曲临界载荷分析的微分求积法．阮苗等［9］运用斜(直)坐标系间的转换关系，建立斜坐标下功能梯度斜板的屈曲微分方程，并采用一般微分求积法，求解单向均布轴压作用下四边固支斜板的屈曲临界载荷．在斜(直)坐标系间，固支边界条件表达式相同;简支边界条件表达式却不同，且其不能由斜(直)坐标系间的转换关系得到．

以往针对斜板的屈曲承载力研究以介绍数值分析方法为主，未系统、全面地进行变参数研究．文中将在横向集中载荷作用下斜板弯曲控制微分方程［10］的基础上，给出斜坐标系下简支边应满足的数学关系式、纵向载荷作用下斜板屈曲控制微分方程，同时将调和微分求积法和边界融入法结合起来(以下简称调和边界融入微分求积法)，求解简支斜板屈曲临界载荷;并以受单向轴压或剪应力作用的简支斜板为例，研究线性非均布载荷变化系数、斜板边长比和倾角同屈曲承载力间的耦合作用规律，为斜向肋在仿生箱梁结构中间距和倾角的确定提供指导．

1 调和边界融入微分求积法

一般微分求积法中的插值多项式由xi－xk组成，现将由xi－xk组成的插值多项式变化为关于sin(xi－xk)的插值多项式，一阶权系数计算公式为［11］

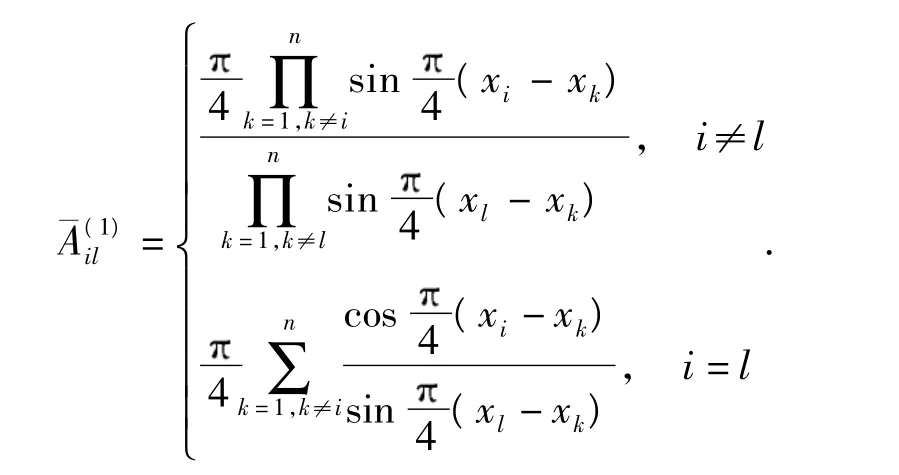
2 简支斜板屈曲控制微分方程

2．1 斜坐标系下的几何方程

下面研究板在发生变形时，中平面内任意一点D的位移与该点应变的关系．斜坐标系下正应变与剪应变的关系如图1所示．xOy为倾角为α的斜坐标系，Oz为垂直于中平面(即板厚度方向)的坐标轴．将板的中平面连同坐标面xOy取出，其上任一点D(x、y)变形后，其位移矢量在坐标轴x、y方向的两个分量为 u(x、y)、v(x、y)．

图1 斜坐标系下正应变与剪应变关系［10］Fig．1 Relation between normal and shear strain in oblique coordinate system［10］

令c=cosα，s=sinα，由图1知，斜坐标系下角度为α的两斜边变形前后正应变和剪应变分别为［10］

根据薄板小挠度弯曲理论中的假定，薄板上任意点的位移u和v与薄板中面上挠度w间的关系为

式(2)中z是位移u和v所在平面与板中面间的距离，取中面以下为正，联立式(1)与(2)，则得斜坐标下弹性薄板的挠度与变形关系:

2．2 斜坐标系下的物理方程

xOy为斜坐标系，Ox轴(Oy轴)方向的扭矩垂直于Ox轴(Oy轴)，因此，需要垂直于Ox轴(Oy轴)作辅助轴ξ(η)，辅助斜坐标系如图2所示．倾角为α的平行四边形斜板DEGF各边应力分布如图3所示．斜板DEGF中左边与下边的应力系统如图4所示．平行四边形DEGF中右边与上边的应力系统如图5所示．针对图4、5中的应力系统进行受力平衡分析得各应力的计算公式如下:

各应力符号所表示的物理意义见文献［10］．

斜坐标下薄板弹性变形与应力间的关系为

图2 辅助斜坐标系Fig．2 Auxiliary oblique coordinate system

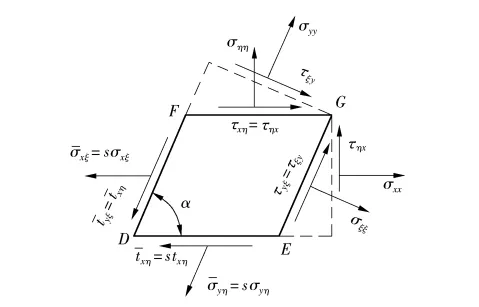
图3 斜板DEGF各边应力分布Fig．3 Stress distribution in each edge for the skew plate DEGF

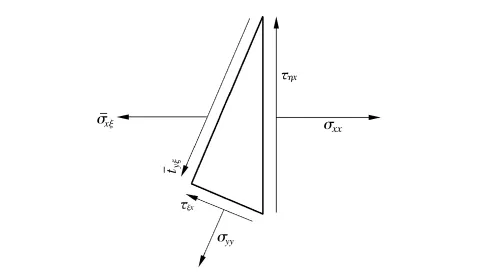
图4 左边与下边的应力系统Fig．4 Stress system for the left and below edges

图5 右边与上边的应力系统Fig．5 Stress system for the right and above edges

2．3 斜坐标系下的力学方程

令D=Eh3/［12(1－2)］，其中 E为材料弹性模量，h为弹性薄板厚度，为材料泊松比．将式(4)代入式(5)，将 σxξz、σyηz和 txηz沿板厚方向作积分，得到斜板弯矩(Mxξ和 Myη)、扭矩(Tyξ和 Txη) 与挠度间的关系为

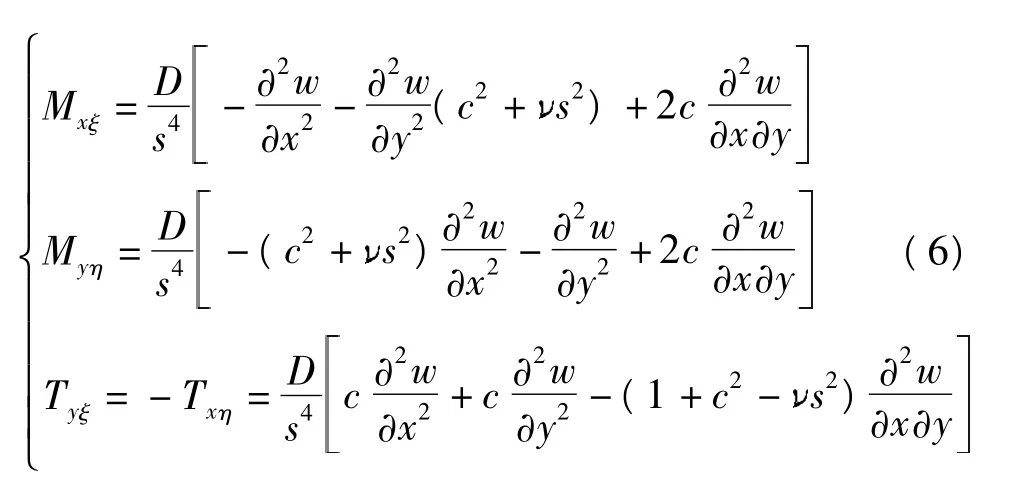
斜坐标系下长、宽分别为dx、dy的平行四边形微元体上，作用纵向载荷Nx、Ny和Nxy，如图6所示．

由图6可见，在纵向载荷 Nx、Ny和 Nxy的作用下，微元体上会产生Oz轴方向的剪力Qξ和Qη，微元体上各边会产生弯矩 Mxξ、Myη和扭矩 Tyξ、Txη．图 6中所有力在Ox、Oy和Oz轴上进行投影求和，根据静力平衡条件∑Fx，y，z=0 得:

图6 纵向载荷作用下微元体的受力平衡Fig．6 Load－carrying equilibrium for the micro－body in the plate subjected to the in－plane load

根据力矩平衡条件∑Mξ=0，∑Mη=0得:

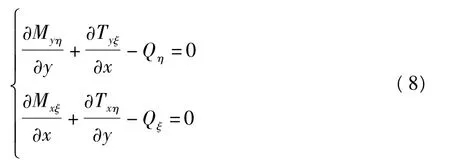
将式(8)中左、右两式分别对y和x微分一次，利用式(7)消去 Qξ和 Qη，并注意 － Txη=Tyξ，则得:

将式(6)代入式(9)，得到斜板的屈曲微分方程:

2．4 调和边界融入微分求积法计算格式

斜板在x轴向的长度为a，在y轴向的长度为b，在区间0≤x≤a和0≤y≤b上，均取n个节点采用切比雪夫(Chebyshev)极值点划分节点［12-13］，可以保证插值余项误差较小，按式(11)划分网格节点．

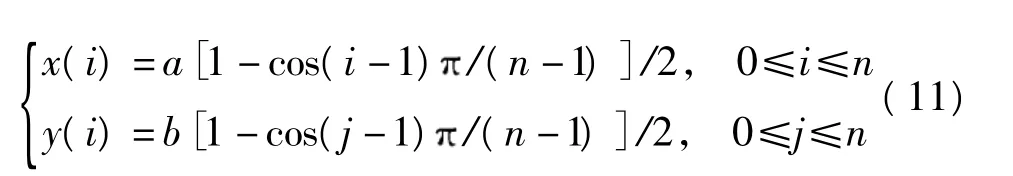
边界上各点构成矩阵为

简支边界上各点弯矩为0，应满足下式:

采用边界自由度融入法，将简支边界上各点的一阶导数作为自由度，边界上各自由度构成矩阵为

当斜板倾角α=90°时，线性非均布载荷变化系数γ=0表示受均布压应力作用;0＜γ≤1表示仅受压应力作用;1＜γ≤2表示受拉(压)应力的混合作用，且以压应力为主;γ=2表示纯弯曲作用．单向轴压和剪应力作用下中间点HI=［wij］(i=2，3，…，n－1;j=2，3，…，n－1)上屈曲微分方程对应的微分求积法计算格式为:

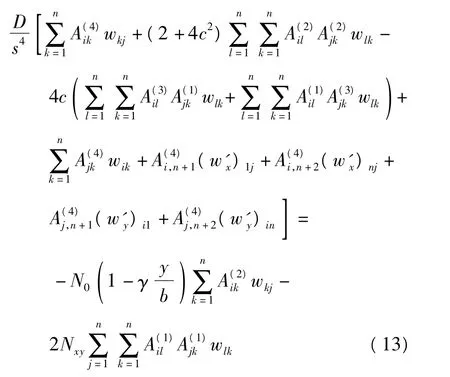
联立式(12)、(13)，得到斜板屈曲控制方程的调和边界融入微分求积法矩阵:

式(14)中消去与边界点 HB=［HB'，HB″］T相关的4n行，得关于中间点HI的n－2阶方阵．边界条件自由度与内部节点自由度间的转换矩阵T=－(KBB)－1KBI，矩阵(PIBT+PII)－1(KIBT+KII)的特征值与纵向载荷N0或Nxy的乘积为斜板屈曲临界载荷．

3 算例

3．1 精确性验证

以两对边受线性非均布轴压(0≤γ≤2)或剪应力作用下四边简支斜板为例，研究边长比(r=b/a)1/2≤r≤2、倾角30°≤α≤90°时，简支斜板屈曲临界载荷的耦合作用规律．文中方法求得的数值解同以往结果对比分析如表1和2所示．由表1可见，对于1/4≤r≤1的剪应力作用下的矩形板，文中方法求得的数值解相对于文献［1］的数值解误差较小．由表2可见，对于边长比r=1的均布轴压作用下的斜板，文中方法求得的数值解相对于文献［14］的数值解误差同样较小．通过对比研究表明，调和边界融入微分求积法在斜板屈曲分析中精度高、稳定性好．

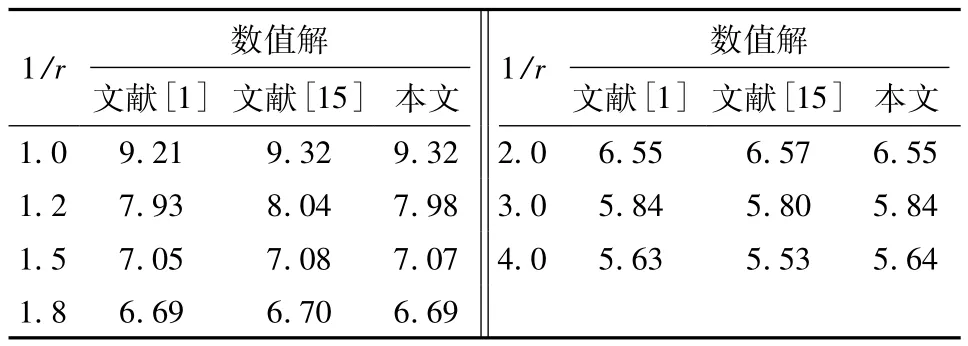
表1 剪应力作用下矩形板数值解对比Table 1 Comparison of numerical solutions for rectangular plates under the shear force

表2 边长比r=1时均布轴压作用下数值解对比Table 2 Comparison of numerical solutions for skew plates under uniform pressure as the aspect ratio of 1

3．2 单向轴压作用下载荷变化系数、斜板边长比及倾角对简支斜板屈曲临界载荷的影响

斜板在线性非均布载荷作用下，当载荷变化系数增大时，轴压中压应力比例减小，屈曲失稳模态在加载边方向分布长度减小．载荷变化系数对简支斜板屈曲临界载荷的影响如图7所示．

由图7可见，不同边长比或倾角下，屈曲临界载荷随载荷变化系数的增大而增大，薄板由平面状态到曲面状态，轴压做功克服薄板应变势能所需能量增大，且增长趋势逐步变大．通过绘制模态变形图发现，当边长比r=1、倾角α=75°时，随着载荷变化系数的增大，屈曲失稳最大挠度值由0．3045m(γ=0)逐步变为0．4064m(γ=2)，失稳模态始终保持为1阶，失稳模态中心由斜板中心(γ=0)逐步向受压区域转移，挠度值由单一负值变为正负值相间，有形成2阶模态的趋势．

图7 单向轴压作用下载荷变化系数对斜板屈曲临界载荷的影响Fig．7 Impact of the load－varying coefficient on the critical buckling load for skew plates under uniaxial pressure

简支斜板在单向轴压作用下，边长比变化对屈曲临界载荷的影响如图8所示．

图8 单向轴压作用下斜板边长比对屈曲临界载荷的影响Fig．8 Impact of the aspect ratio on the critical buckling load for skew plates under uniaxial pressure

由图8可见，不同载荷变化系数或倾角下，屈曲临界载荷均随边长比的增大而先增大后减小再增大，薄板由平面状态到曲面状态，轴压做功克服薄板应变势能所需能量依次增大、减小、增大．通过绘制模态变形图发现，当载荷变化系数γ=1、α=90°时，随着边长比的增大，屈曲失稳最大挠度值由0．2793m(γ=0)逐步增加到 0．3180 m(γ =2)，失稳模态由2阶转化为1阶．

简支斜板在单向轴压作用下，倾角变化对屈曲临界载荷的影响如图9所示．

由图9可见，不同载荷变化系数或边长比下，屈曲临界载荷随倾角的增大而减小，薄板由平面状态到曲面状态，轴压做功克服薄板应变势能所需能量减小．通过绘制模态变形图发现，当载荷变化系数γ=0、边长比r=1时，随着倾角的增大，屈曲失稳最大挠度值先增加后减小，失稳模态由2阶变为1阶，2阶和1阶失稳模态长轴分别位于斜板长(短)对角线方向．

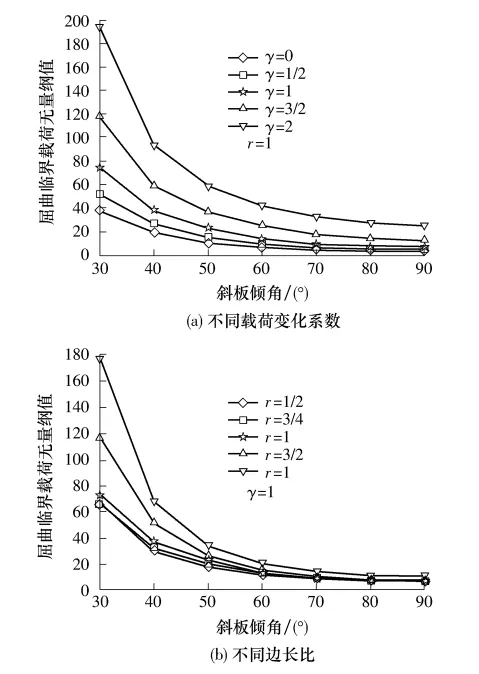
图9 单向轴压作用下斜板倾角对屈曲临界载荷的影响Fig．9 Impact of skew angles on the critical buckling load for skew plates under uniaxial pressure

3．3 剪应力作用下斜板边长比及倾角对简支斜板屈曲临界载荷的影响

图10 剪应力作用下斜板边长比对屈曲临界载荷的影响Fig．10 Impact of the aspect ratio on the critical buckling load for skew plates under shear force

剪应力作用下边长比变化对简支斜板屈曲临界载荷的影响如图10所示．由图10可见，不同倾角下屈曲临界载荷随边长比增大而增大，薄板由平面状态到曲面状态，剪应力做功克服薄板应变势能所需能量增大．通过绘制模态变形图发现，当倾角α=90°时，随着边长比的增大，屈曲失稳最大挠度值先减小后增大，失稳模态始终保持为1阶，失稳模态长轴由斜板短对角线方向过渡到长对角线方向．

剪应力作用下斜板倾角变化对简支斜板屈曲临界载荷的影响如图11所示．

图11 剪应力作用下斜板倾角对屈曲临界载荷的影响Fig．11 Impact of skew angles on the critical buckling load for skew plates under shear force

由图11可见，不同边长比下屈曲临界载荷随倾角的增大先减小后增大，薄板由平面状态到曲面状态，剪应力做功克服薄板应变势能所需能量先减小后增大．通过绘制模态变形图发现，当边长比r=1时，随着倾角的增大，屈曲失稳最大挠度值先增加后减小，失稳模态由2阶转化为1阶，2阶失稳模态长轴分布在斜板长对角线方向，随着角度增大，1阶失稳模态长轴由斜板短对角线方向过渡到长对角线方向．

4 结语

文中将调和微分求积法和边界融入法结合起来，给出调和边界融入微分求积法求解简支斜板局部稳定性的具体方法．与其他数值解对比分析表明，采用调和边界融入微分求积法求解简支斜板局部稳定性，数值解精度高、稳定性好．

系统研究了线性非均布载荷变化系数、斜板边长比和倾角同斜板屈曲承载力间的耦合作用规律．在进行仿生箱梁结构加劲肋布置设计时，根据箱梁结构参数，确定结构局部失稳的主要受载因素是轴向压应力还是剪应力，结合主要受载因素作用下斜板屈曲承载力的变化规律，对加劲肋进行间距和倾角的仿生布置设计，如梁高(或梁宽)很大而腹板(或翼缘板)较薄时，轴向压应力较为重要．

［1］ Lotfi S，Azhari M，Heidarpour A．Inelastic initial local buckling of skew thin thickness－tapered plates with and without intermediate supports using the isoparametric spline finite strip method ［J］．Thin－Walled Structures，2011，49:1475－1482．

［2］ 陈炎，黄小清，马友发．单向轴压下压电矩形薄板的后屈曲问题［J］．华南理工大学学报:自然科学版，2003，31(8):45－49．Chen Yan，Huang Xiao－qing，Ma You－fa．Post－buckling of piezoelectric rectangular plate under unilateral pressure［J］．Journal of South China University of Technology:Natural science Edition，2003，31(8):45－49．

［3］ Ganapathi M，Prakash T．Thermal buckling of simply supported functionally graded skew plates［J］．Composite Structures，2006，74(2):247－250．

［4］ Xiang Y，Wang C M．Buckling of skew Mindlin plates subjected to in－plane shear loading ［J］．International Journal of Mechanical Sciences，1995，37(10):1089－1101．

［5］ Farajpour A，Shahidi A R，Mohammadi M，et al．Buckling of orthotropic micro/nanoscale plates under linearly varying in－plane load via nonlocal continuum mechanics［J］．Composite Structures，2012，94(5):1605－1615．

［6］ Dehghan M，Baradaran G H．Buckling and free vibration analysis of thick rectangular plates resting on elastic foundation using mixed finite element and differential quadrature method ［J］．Applied Mathematics and Computation，2011，218(6):2772－2784．

［7］ Wang X W，Shi X D．Differential quadrature buckling analyses of rectangular plates subjected to non－uniform distributed in－plane loadings ［J］．Thin－Walled Structures，2006，44:837－843．

［8］ Wang X W，Gan L F．New approaches in application of differential quadrature method to fourth－order differential equations［J］．Communications in Numerical Methods in Engineering，2005，21:61－71．

［9］ 阮苗，王忠民．功能梯度斜板的屈曲分析［J］．机械工程学报，2011，47(6):57－61．Ruan Miao，Wang Zhong－min．Buckling analysis of functionally graded skew thin plate［J］．Journal of Mechanical Engineering，2011，47(6):57－61．

［10］ 李国豪．关于斜交异性板的弯曲理论［J］．同济大学学报:自然科学版，1997，25(2):121－126．Li Guo－hao．On the bending theory of skew anisotropic skew plate［J］．Journal of Tongji University:Natural Science Edition，1997，25(2):121－126．

［11］ Ömer Civalek．Application of differential quadrature(DQ)and harmonic differential quadrature(HDQ)for buckling analysis of thin isotropic plates and elastic columns［J］．Engineering Structures，2004，26(2):171－186．

［12］ Mansour Mohieddin Ghomshei M，Mahmoudi A．Thermal buckling analysis of cross－ply laminated rectangular plates under nonuniform temperature distribution:a differential quadrature approach［J］．Journal of Mechanical Science and Technology，2010，24(12):2519－2527．

［13］ Wu X H，Ren Y．Differential quadrature method based on the highest derivative and its applications［J］．Journal of Computational and Applied Mathematics，2007，205:239－250．

［14］ Wang X W，Tan M，Zhou Y．Buckling analyses of anisotropic plates and isotropic skew plates by the new version differential quadrature method ［J］．Thin－Walled Structures，2003，41:15－29．

［15］ Saadapour M M，Azhari M，Bradford M A．Buckling of arbitrary quadrilateral plates with intermediate supports using the Galerkin method ［J］．Comput Methods Appl Mech Eng，1998，164:297－306．

［16］ Yoshimura Y，Iwata K．Buckling of simply supported oblique plates［J］．Journal of Applied Mechanics，1963，30(2):363－366．

［17］ Durvasula S．Buckling of simply supported skew plates［J］．Journal of the Engineering Mechanics Division，1971，97(3):967－979．

［18］ Hegedus T．Finite strip buckling analysis of skew plates under combined loading［M］∥Evayi M．Stability of steel structures．Budapest:Akademi Kiado，1988:633－641．