数学建模中解题策略的教学探究
2013-07-31郭啸
郭 啸
(长沙师范学院初等教育系,湖南长沙410100)
数学建模中解题策略的教学探究
郭 啸
(长沙师范学院初等教育系,湖南长沙410100)
数学问题的解题策略能在数学建模过程中为选择建模方法和制定建模步骤提供重要指导.本文总结了数学建模中基本的解题策略,探讨了数学建模解题策略的教学原则.结合具体案例在数学建模中开展实施解题策略教学的探索与实践,为数学建模中解题策略的教与学提供了有价值的参考.
数学建模;解题策略;案例教学
1 前言
随着高等教育教学的改革,大学生问题解决能力的培养已成为数学建模课程和实践活动的核心目标.教育心理学的研究(邵瑞珍,1990)表明,传授学生有效的解题策略,加强对学生解题策略的训练是培养学生问题解决能力的最有效做法.我国数学教育界对解题策略课题的研究起步较晚,与数学建模结合的系统理论尚未形成.本文总结数学建模问题中的基本解题策略,结合案例探讨如何在数学建模中开展解题策略的教学和训练.
2 解题策略的内涵与意义
数学问题解题策略是指在解决数学问题的过程中,借以思考假设、选择和采取解决方法与步骤的方针与规则[1],它是对解题途径的概括性认识[2].数学建模是使用数学方法解决实际应用问题,数学建模过程是积极进行思维加工的活动过程,自然会受到数学解题策略思维的影响.数学问题解题策略能为建模策略的确定、选取解决方法和制定解决步骤提供重要指导.关于数学建模认知机制的研究表明[3],掌握一般性的解题策略有助于数学建模过程的顺利进行,在数学建模教学中融入一般性解题策略知识能提高学生的数学建模能力.
本文在已有的研究基础上[4][5],结合数学建模竞赛中的问题分析,将数学建模中常用的基本解题策略归纳如下.
2.1 模式识别
在长期解决数学问题的过程中,主体对所积累的知识经验进行加工,根据问题的目标和规律逐渐总结出典型结构与重要类型——[6]模式.当遇到新问题时,首先要辨别题目的类型属于哪种模式,以便与已有的知识经验发生联系,这就是模式识别的解题策略.
2.2 化归变换
当问题难以直接解决时,根据问题的性质、关系等特点,通过转化过程将其归结为另一个比较容易解决的或已经解决过的等价问题.它所使用的方法主要就是将数学问题表述形式进行等价转化,转换的原则就是:简单化、熟悉化、直观化.除了问题表述的等价转化,将问题分为几个小问题也属于化归变换.
2.3 有效增设
在不改变问题目标和性质的前提下,增加条件使问题的解决更容易,这就是有效增设.构造辅助元素方法、对偶法、设置作为子目标的一个或多个中间结论的方法、挖掘隐含条件优化假设等均是这一策略的具体体现.
2.4 整体策略
从问题的整体结构出发进行观察、分析、处理,从全局上把握条件与结论及其间联系,把握解题各部分、各环节间的联系,应摆脱陷于局部细节中一时难以弄清的复杂计算与繁琐讨论,避免各解题环节的脱节与孤立.通常所要求的在解题中进行多向立体思维、思路探索中的及时反馈-评价-调控及解题后的全面反思等方法都是这一策略的具体体现.
3 数学建模中解题策略的教学研究
3.1 教学原则
3.1.1 重视解题策略的知识性教学,开展样例教学
根据对数学建模认知的研究表明[3],专家和新手在解决问题时所使用的策略方面存在着差异,相当部分学生希望老师教给他们一般的思维策略与方法.因此,在数学建模教学中,教师应当将解决数学问题的一般思维策略提炼出来,较为系统化地讲授给学生.但解题策略比较宽泛,在与数学建模的结合上也较为薄弱.样例教学是向学生书面呈现一批解答好的例题,学习、研究别人已建立的现成数学模型及数学建模的思想方法.在这些丰富的数学建模问题中蕴含着大量具体的数学建模策略性知识,样例教学是让学生在领悟与模仿中建立数学建模解题策略知识认知结构的基本教学策略.
3.1.2 加强解题策略的元认知训练,实施变式练习
国内外已有关于问题解决思维策略训练研究的结果(AlisonKin,1991,p307-317;程素萍,1996,pl6-19)表明,元认知策略监控、指导思维策略的运用,元认知训练比一般思维训练具有更好的作用.一般思维策略训练更多地关注解题策略的含义,属于知觉水平的教学,其结果是学生可能了解使用策略的程序,但无法掌握策略的应用.将解题思维策略教学与元认知训练结合起来,使学生将注意力不仅指向问题本身的加工而且指向自己加工策略的认知过程、教学中通过设置不同的问题情境,将一个策略原型迅速而恰当地提炼、转变到某一模型上;或是将一个领域内的模型快捷、灵活地转移到另一个领域.在变式练习中让学生体会策略选择、加工、调节的过程,领悟评价各种数学建模策略的方法,增强学生对如何使用解题策略的元认知训练.
3.2 教学案例
教学中可以开展历年大学生数学建模竞赛赛题分析和总结将增加学生的解题策略知识,提高策略模式的识别和应用能力.比如,图论理论和方法在大学生数学建模竞赛中都有广泛应用,如欧拉图、染色、最短路等.但是实际问题的解决往往是在对已有模型采用多种解题策略实施加工改进的创新应用.下面结合2012年全国大学生数学建模D题给出解题策略的一个教学案例.
问题1提出的一个机器人在二维固定场景中的避障问题,行走规则和障碍物的数学描述等详见[6].以下分析讲解本题第一问,不考虑机器人移动时间,设计从指定起点到达指定目标点的最短避障路径.
解题策略分析:从给出的平面场景看,由于机器人并没有指定的移动路径,所以本题没有给出网络图,想通过模式识别直接应用已有的图论问题模型求解并不可行.如果能通过分析给出可行路径的范围,在这个范围内寻找最短路径则可以借鉴图论模型解决.于是本题分解为两个子问题:寻找可行路径图→得到连通图求指定两顶点的最短路径.这种将问题分解是化归变换策略最常见的一种应用.
首先解决求解从O点到A点的可行路径问题.两点间直线距离最短,若将O点与A点用直线连接则穿过了障碍物,但实际行走时不能穿过障碍物.可假设该直线有弹性,为绕过障碍物且保持直线拉伸距离最小,所以直线被拉伸后必然与障碍物边沿相切.由于拉伸方向不同,产生的可行路径有多条.机器人只以圆弧路径转弯,经过的路障顶点要进行圆角化,在路障顶点处增加10个单位半径为10个单位的圆见图1,路径为OE—EF—FB,OG—GH—HB.以上寻找可行路径的思想就是从原题中挖掘内涵,增加条件解决问题,这就是有效增设策略.有效增设策略在历年数学建模赛题中都有使用,包括增添辅助参数、设置区域划分、引入过程变量.通过比较可行路径,可得到最短路径即O→E→F→B长度约为271.
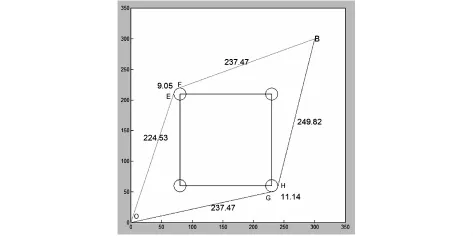
图1
题目还要求找出O到其余多点的最短路径,避障网络图更加复杂见图2.在图论中图2中网络图是连通图,去掉回路中的任何边都不会影响图的连通性质.意识到这个本质特征,则求最短路径就等价于寻找权重之和最小的生成树,即最小生成树问题.这种通过问题的分析,摆脱非本质因素的干扰和束缚抽取问题的本质特征,对问题进行准确的模式识别和归类的解题策略,这就是在数学建模中最常用的模式识别策略.

图2
通过分析并结合O点到A点最短路的求解过程,让学生得出解题策略:增设障碍物的圆角寻找有效切线→化归分解先找出可行路径→转换得到连通图→应用图论的最小生成树模型求解.以从O点到B点为例下面给出解决方案. O→B点有效路径的连通图见图3,通过求解最小生成树可以得到O→B点的最短路径为O→B1→B3→C1→C3→D1→B.
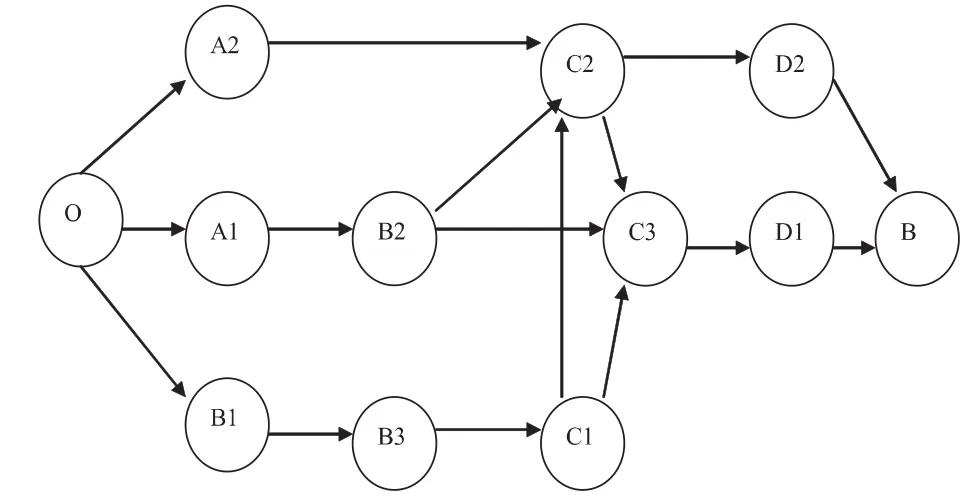
图3
〔1〕李明振.数学问题解决策略及其训练研究[J].贵州师范大学学报(自然科学),1998(2):72-76.
〔2〕黄超骏.高中数学解题策略与策略性知识的教学[D].重庆:西南师范大学,2002.
〔3〕李明振.数学建模的认知机制及其教学策略研究[D].重庆:西南大学,2007.
〔4〕罗增儒.数学解题学引论[M].西安:陕西师范大学出版社, 2008.361-433.
〔5〕江高文.数学新思维:中学数学思维策略与解题艺术[M].武汉:华中师范大学出版社,2002.2-52.
〔6〕2012年高教社杯全国大学生数学建模竞赛赛题:http:// www.mcm.edu.cn/problem/2012.
O242
A
1673-260X(2013)12-0007-02
