Diffusion-controlled Adsorption Kinetics of Surfactant at Air/Solution Interface

LIU Junji (刘俊吉)*, XU Yun (徐芸) and SUN Hongxiu (孙红秀)

School of Science, Tianjin University, Tianjin 300072, China

Diffusion-controlled Adsorption Kinetics of Surfactant at Air/Solution Interface

LIU Junji (刘俊吉)*, XU Yun (徐芸) and SUN Hongxiu (孙红秀)

School of Science, Tianjin University, Tianjin 300072, China

For the diffusion-controlled adsorption, the expression of dynamic surface adsorption Γ (t) was obtained by solving the diffusion equation. Two cases, i.e. the short and long time limits, were mainly discussed in this paper. From the measured dynamic surface tension of aqueous surfactant sodium dodecyl sulfate (SDS) solutions at 25 °C, the adsorption kinetics of SDS at air/solution interface was studied. It was proved that for both of the short and long time limits, the adsorption process of SDS was controlled by diffusion.

adsorption, air/solution interface, dynamic surface tension

1INTRODUCTION

The adsorption kinetics of aqueous surfactant solutions at air/solution interface plays a very important role in wetting, foam stability, emulsion stability, fast coating, detergency, surface oscillation and adsorptive bubble separation technique etc. Therefore, a lot of research papers [1-24] focused on this field. For the adsorption process of aqueous surfactant solution at the air/solution interface, the whole process consists of two steps. The first step is the transport of surfactant molecules from the bulk phase to the subsurface due to concentration gradient, i.e., the diffusion step, and the second one is the transport of molecules from the subsurface to the surface, i.e., the adsorption step. If the rate of the first step is much slower than that of the second one, the whole process is controlled by diffusion. This kind of diffusion-controlled adsorption will be discussed in this paper.

The diffusion-controlled adsorption kinetics was first treated quantitatively by Ward and Tordai [1]. An expression for the dynamic surface adsorption Γ (t), i.e., the famous Ward-Tordai-Equation, was derived and always cited by the authors studied the adsorption kinetics. In this paper, we focused on the discussion of Ward-Tordai-Equation in both of the short and long time limits.

Surfactant sodium dodecyl sulfate (SDS) was chosen and the dynamic surface tensions of its aqueous solutions were measured by means of the maximum bubble pressure method. In the previous studies on SDS, there were conflicting conclusions [16-20]. The diffusion controlled [17], kinetic limited [18], and mixed diffusion-kinetic [19, 20] process were reported. This is the reason why SDS was chosen to be studied in this paper. Its adsorption kinetics was studied on the base of theoretical work.

2THEORY

When the whole process is dominated by diffusion, then the diffusion equation (Fick’s second law) is used,

where (,)c x t is the concentration at distance x and time t, and D represents the diffusion coefficient of surfactant in water.

In order to solve Eq. (1), the following initial condition (i.c.) and boundary condition (b.c.) are necessary:

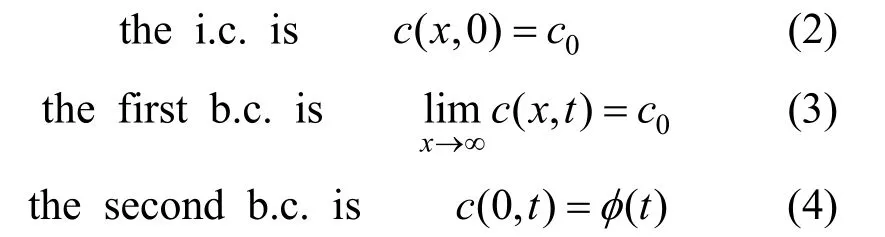
where c0is the bulk concentration of aqueous surfactant solution, and φ (t)is subsurface concentration (concentration at 0x=).

By means of Laplace transformation, the solution of Eq. (1) under the above conditions [Eqs. (2)-(4)] is

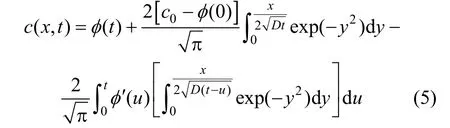
To get the surface adsorption, Fick’s first law should be used at 0x=,

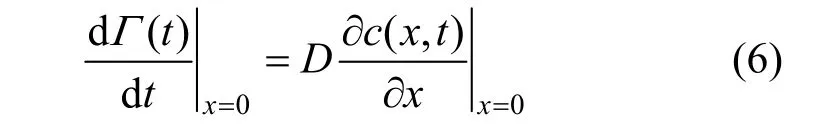
Inserting Eq. (5) into Eq. (6) and integrating it, the diffusion amount of the surfactant molecules from the subsurface to the surface in the time range 0t→can be obtained as

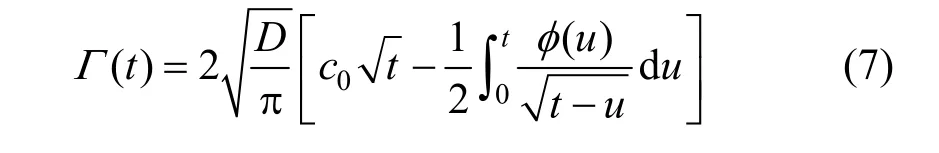
The following two cases are always discussed.

2.1Short-time limit (0→t)

At the beginning of adsorption, the subsurface concentration is zero, i.e.

then, Eq. (7) is reduced to

2.2Long-time limit

After a certain long time t1, the subsurface concentration will also trend to a constant assumed as cs(Fig. 1). Then, the whole time range can be divided into two parts: 0→t1and t1→t. For the first time range, there is

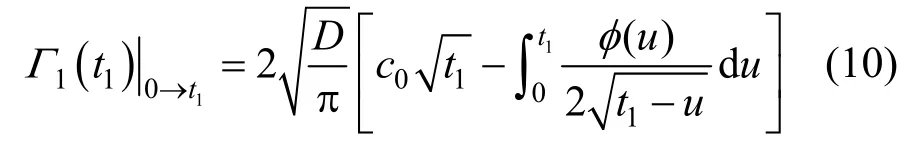
Figure 1Schematic diagram of subsurface concentration

For the second one (1tt→), there is

Then, for the whole time range (0t→), the following Eq. (12) can be deduced as

It is difficult to measure the dynamic surface adsorption Γ( t), however, the dynamic surface tension γ( t ) is easy to be measured. Therefore, it is necessary to find the relationship between γ( t) and Γ( t).

2.3Relationship betweenΓ (t)andΓ (t)

Gibbs’ adsorption equation can be used to describe the adsorption of surfactant on the surface of the aqueous solution.

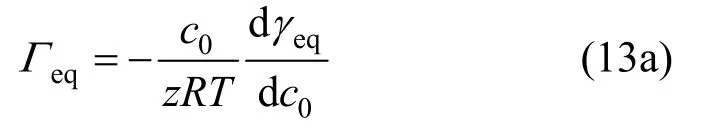
where γeqis the equilibrium surface tension, c0is the bulk concentration and z is a factor, which equals 2 for surfactant SDS.

Equation (13a) can be rearranged as

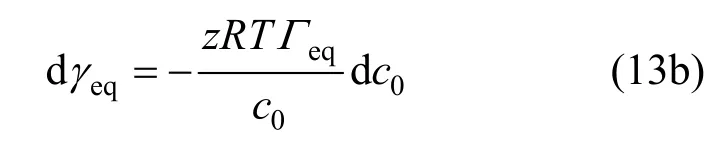
Combing with the Langmuir isotherm,Γeqcan be given by

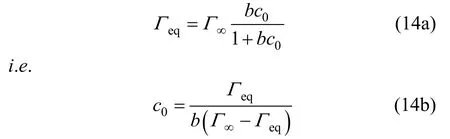
One can get

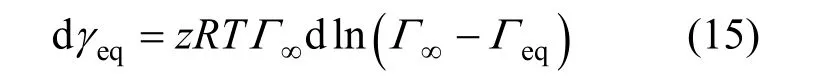
This equation indicates the relationship between the equilibrium surface tension γeqand the equilibrium adsorption Γeq.

It is well known that the surface tension γ depends only on the surface adsorption Γ. It means that the surface tension γ is only a function of the surface adsorption Γ. Here, one can also use this equation in the non-equilibrium adsorption process.

Integrating Eq. (15) yields

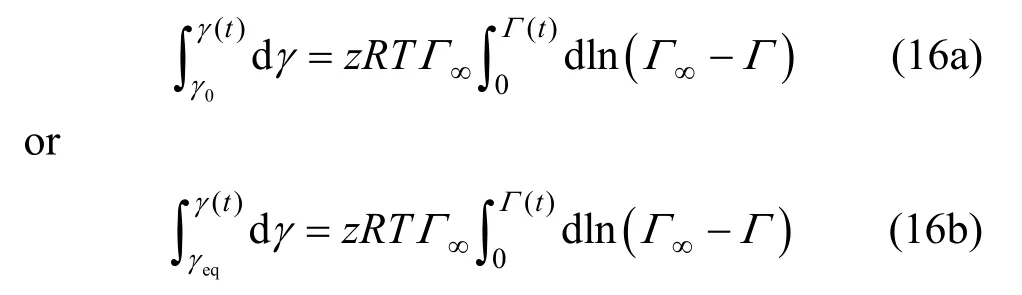
where Γ0x is the equilibrium surface tension of water (pure solvent).

Simplifying these two equations, one gets

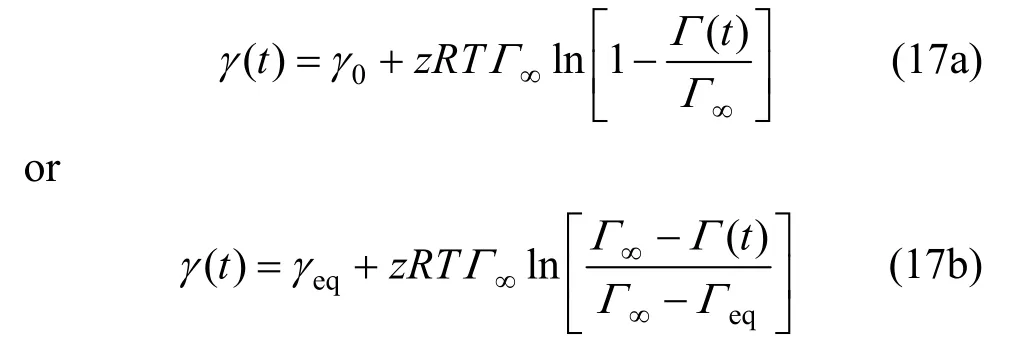
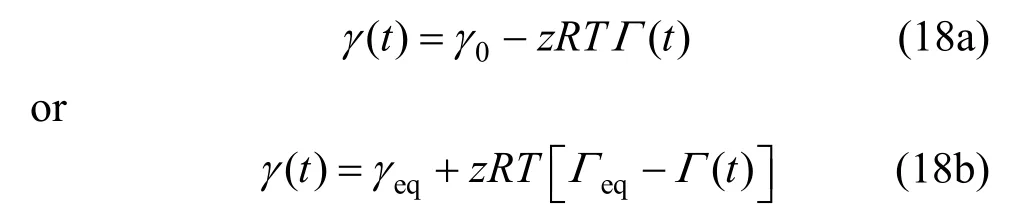
Substituting Γ (t) [Eq. ( 9)] into Eq. (18a), there is

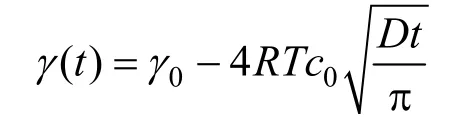
(for the short time limit adsorption)(19) Substituting Γ (t) [Eq. (12)] into Eq. (18b), Eq. (20) can be obtained as

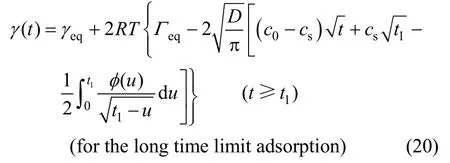
These two equations show that for the two limit cases, the short and long time adsorption, there should be a linear relationship between Γ (t) and t.

Equations (9) and (19), the results for the short time limit, were well known and always adopted to discuss the experimental data in the literatures [1, 13-15, 21-23]. However, the results, i.e. Eqs. (12) and (20) in our paper, have never been reported by the others. They could be used to treat the experimental data and determine the adsorption mechanism as t→∞.

3EXPERIMENTAL

The equilibrium surface tensions were measured with Wilhelmy plate tensiometer (K12 from the Company Krüss GmbH Hamburg, Germany). The measurements of dynamic surface tension were carried out by means of a maximum bubble pressure tensiometer (BP-2 made by Krüss GmbH Hamburg, Germany). The measuring range in the time window is from 0.005 to 60 s. The capillary diameter is d=0.264 mm. Surfactant sodium dodecyl sulfate (SDS) was obtained from SIGMA-ALDRICH Chemie GmbH, Fluka, Swiss. The surfactants were used without any further purification. Three aqueous surfactant solutions were prepared using double distilled and deionized water. The last distillation was performed over alkaline KMnO4in order to remove the effect of surface active impurities. All measurements of dynamic surface tension were performed at (25±0.1) °C.

4RESULTS AND DISCUSSION

To determine the critical micelle concentrations (CMC) of surfactant SDS, the equilibrium surface tensions γeqof its aqueous solutions are measured and plotted in Fig. 2. The CMC at 25 °C is 7.6×10−3mol·L−1. In the adsorption kinetics studies, the concentrations should be below CMC so that the effect of micelle on adsorption does not exist.

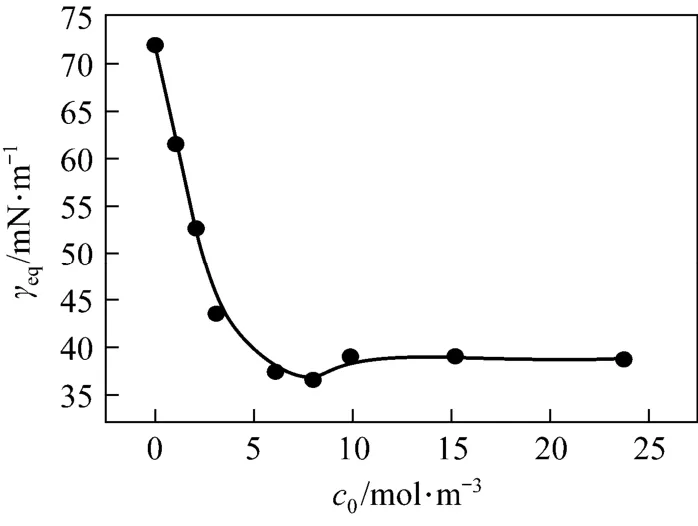
Figure 2Equilibrium surface tensions of aqueous SDS solutions

The measured dynamic surface tensions of aqueous SDS solutions at 25°C are shown in Fig. 3. For all the three pre-CMC concentrations at the shortest measuring time (about 5 ms), the value of surface tension of pure solvent (γ0) is reached. It indicates that the new created surface in solution is occupied only by the solvent molecules and the adsorption does not yet happen. With increasing time, the dynamic surface tension γ(t) decays rapidly within 5 s. This is the result of adsorption of surfactant at the surface. After about 5 s, γ(t) reaches a constant value. The surface is fast full-occupied and there are few free adsorption positions at the surface. Then, the adsorption rate should tend to zero, i.e., Γd( t)/dt≈0.

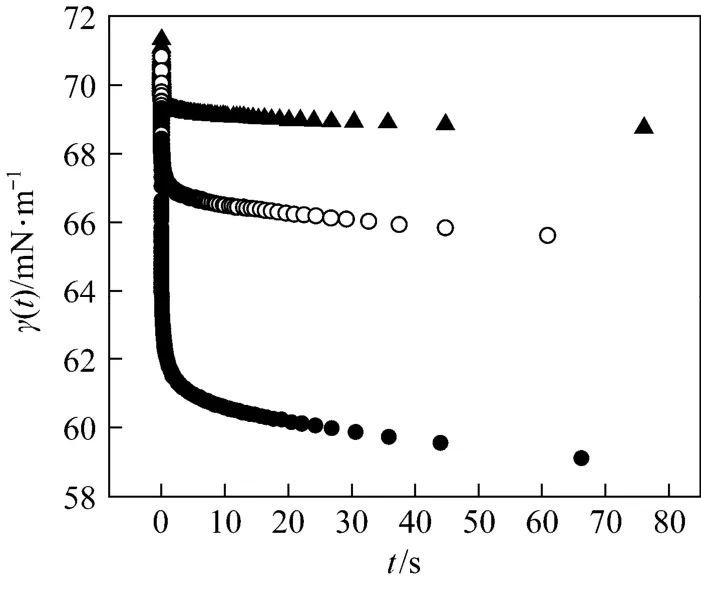
Figure 3Dynamic surface tensions of aqueous SDS solutions▲ 1.054×10−3mol·L−1; ○ 2.081×10−3mol·L−1; ● 3.939×10−3mol·L−1

By using Eqs. (17a) and (14a) in equilibrium state, Γ∞can be fitted from the experimental equilibrium surface tensions. The fitted result is Γ∞=8.82×10−6mol·m−2for SDS. Then, the calculated -t Γ (t) by means of Eq. (17a) is shown in Fig. 4. It is found from Fig. 4 that the adsorption rate at the beginning is much faster than at the end. The adsorption happens mainly in the initial stage. This phenomena can be interpreted as that at the beginning the surface is empty enough toadsorb the arrived surfactant molecules and the surface adsorption Γ (t) will increase with time rapidly. However, at the end of adsorption, Γ (t) will tend to a constant and d/d tΓ (t) will approach to zero. Eqs. (9) and (12) can be combined as

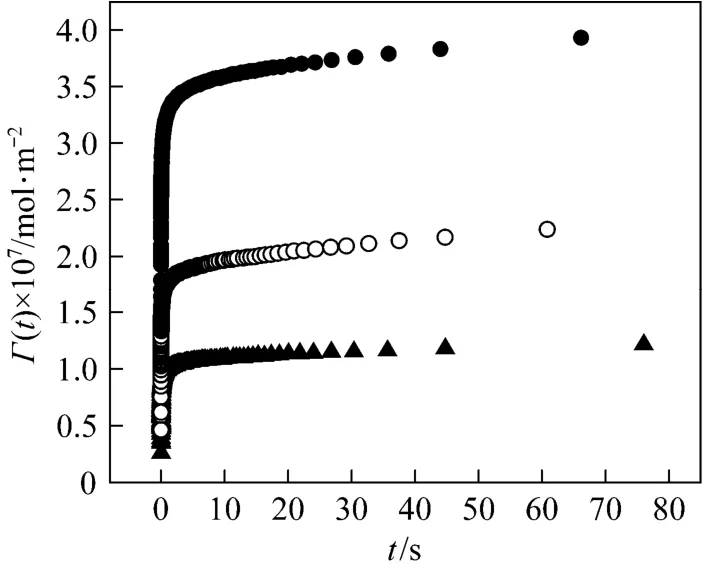
Figure 4The dynamic surface adsorptions of aqueous SDS solutions▲ 1.054×10−3mol·L−1; ○ 2.081×10−3mol·L−1; ● 3.939×10−3mol·L−1

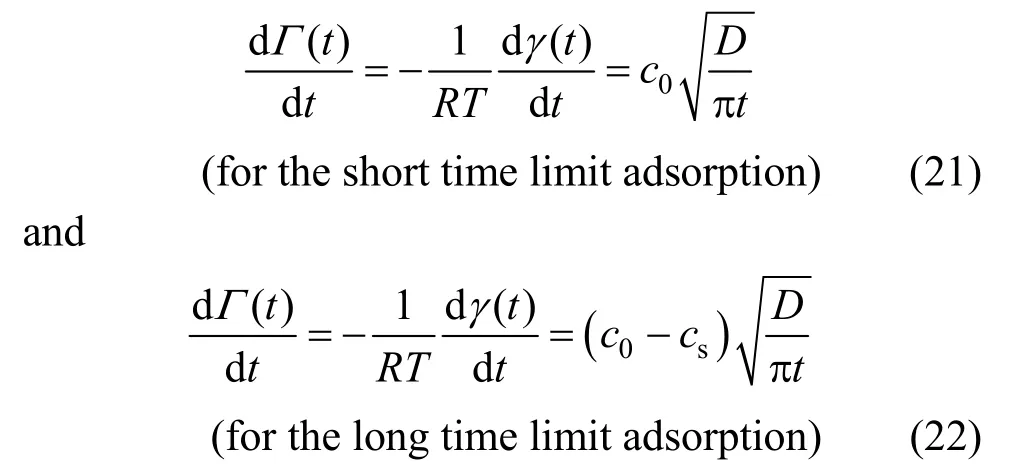
For the shot time limit (t→0), the adsorption rate (dΓ( t)/d t) should be very high. But for the long time limit (t→∞), there is cs→c0in most cases and the adsorption rate (dΓ( t)/d t) should be very small and tends to zero. The calculated Γ( t) from the experimental γ( t) shows such results (Fig. 4).

For diffusion-controlled adsorption, the reduction of γ( t) should follow a square-root decay in the short time limit, corresponding to Eq. (19). Plotting γ( t)-tin Fig. 5, there are good linear relations for all three pre-CMC concentrations. It means that the adsorption is really controlled by diffusion in the short time range. This conclusion is consistent with that of the previous study by Joos [17]. From the slope of the lines, the apparent diffusion coefficient of the surfactant in water can be calculated [Eq. (19)]. The calculated results are listed in Table 1. It is shown that the apparent diffusion coefficient is slightly concentration-dependent.

For the long time limit, there should also be the linear relationship between γ( t) and t according to Eq. (20) although the values of the constant variables γeq, Γeq, csand t1are unknown. The experimental results demonstrate such linear relation (see Fig. 6) as expected. It indicates that for these three concentrations the adsorption is also controlled by the diffusion in the long time range.

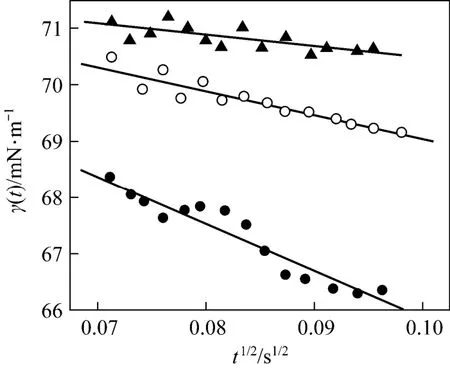
Figure 5The relation between γ(t) and t in the short time limit▲ 1.054×10−3mol·L−1; ○ 2.081×10−3mol·L−1; ● 3.939×10−3mol·L−1

Figure 6The relation between Γ (t) and t in the long time limit▲ 1.054×10−3mol·L−1; ○ 2.081×10−3mol·L−1; ● 3.939×10−3mol·L−1

When the adsorption was controlled by diffusion in both the short and long time ranges, the following equation from Eqs. (20) and (19) can be deduced.

Inserting the experimental results into Eq. (23), the value of cs/c0can be calculated. It equals to about 99.5% for the three concentrations (Table 1). It means that at the end of adsorption (after 8000 ms), the subsurface concentration reach the 99.5% of the bulk concentration (c0) for the aqueous SDS solutions. In this case, the concentration difference ( Δc=c0−cs), i.e., the diffusion force, is very small. The diffusion step is much slower than adsorption step. The whole process is dominated by diffusion in the long timerange for aqueous SDS solution.

Table 1Fitting and calculation results of experimental dada

5CONCLUSIONS

For the diffusion-controlled adsorption, there should be linear relation between Γ (t) and t in both the short and long time limits. The equilibrium and dynamic surface tensions of aqueous sodium dodecyl sulfate (SDS) solutions at 25 °C were measured by means of Wilhelmy plate tensiometer and maximal bubble pressure tensiometer, respectively. From the experimental data, the expected linear relation between γ( t ) andwas obtained. The diffusion-controlled adsorption was proved in both of the short and long time limits. In addition, the diffusion coefficient was calculated from the experimental data in the range of short limit and the subsurface concentration in the long time limit was estimated.

NOMENCLATURE

b adsorption constant in Langmuir isotherm

c0bulk concentration, mol·m−3

cssubsurface concentration after t1

c(x, t) concentration, mol·m−3

D diffusion coefficient, m2·s−1

R ideal gas constant, J·mol−1·K−1

x distance to the subsurface, m

T temperature, K

t time, s

t1assumed long time

u integration variable in Eqs. (5, 7, 10, 12, 20) y integration variable

z factor in Gibbs’ adsorption equation

Γ1(t)0→tdynamic surface adsorption before t1, mol·m−2

1

Γ2(t)t→tdynamic surface adsorption after t1, mol·m−2

1

Γeqequilibrium adsorption, mol·m−2

Γ∞saturation adsorption, mol·m−2

Γ(t) dynamic surface adsorption, mol·m−2

γ0surface tension of the solvent (water), mN·m−1

γeqequilibrium surface tension, mN·m−1

γ(t) dynamic surface tension, mN·m−1

π constant, π=3.141592···

φ( t) subsurface concentration, mol·m−3

REFERENCES

1 Ward, A.F.H., Tordai, L., “Time-dependence of boundary tensions of solutions. 1. The role of diffusion in time-effects”, J. Ch em. Phys.,14(7), 453-461 (1946).

2 Hansen, R.S., “Diffusion and the kinetics of adsorption of aliphatic acids and alcohols at the water-air interface”, J. Colloid Sci.,16, 549-560 (1961).

3 Sutherland, K.L., “The kinetics of adsorption at liquid surfaces”, Austr. J. Sci. Res., A5, 683−696(1952).

4 Petrov, J. G., Miller, R., “On the solution of diffusion problems in adsorption kinetics”, Colloid & Polymer Sci.,255(7), 669-674 (1977).

5 Kao, R. L., Edwards, D. A., Wasan, D. T., Chen, E., “Measurement of interfacial dilatational viscosity at high rates of interface expansion using the maximum bubble pressure method. 1. Gas-liquid surface”, J. Colloid Interf. Sci.,148(1), 247-256 (1992).

6 Liggieri, L., Ravera, F., Passerone, A., “A diffusion-based approach to mixed adsorption kinetics”, Colloid and Surfaces A,114(8), 351-359 (1996).

7 Filippov, L.K., “Dynamic surface tension of aqueous surfactant solutions. 1. Diffusion-converctive controlled adsorption”, J. Colloid Interface Sci.,163(1), 49-60 (1994).

8 Fang, J., Wantke, K., Lunkenheimer, K., “Evalution of the dynamic surface tension of alkylphosphine oxides”, J. Phys. Chem.,99(13), 4632-4638 (1995).

9 Eastoe, J., Dalton, J.S., Rogueda, P.G.A., Griffiths, P.C., “Evidence for activation-diffusion controlled dynamic surface tension with a nonionic surfactant”, Langmuir,14(5), 979-981(1998).

10 Lin, S., Tsay, R., Lin, L., Chen, S., “Adsorption kinetics of C12E8at the air-water interface: Adsorption onto a clean interface”, Langmuir,12(26), 6530-6536 (1996).

11 Gao, T., Rosen, M. J., “Dynamic surface tension of aqueous surfactant solutions. 7. Physical significance of dynamic parameters and the induction period”, J. Colloid Interf. Sci.,172(1), 242-248 (1995).

12 Makievski, A.V., Fainerman, V.B., Miller, R., Bree, M., Liggieri, L., Ravera, F., “Determination of equilibrium surface tension values by extrapolation via long time approximations”, Colloids Surfaces A,122(1-3), 269-273 (1997).

13 Borwankar, R.P., Wasen, D.T., “The kinetics of adsorption of surface active agents at gas-liquid surfaces”, Chem. Eng. Sci.,38(10), 1637-1649 (1983).

14 Eastoe. J., Dalton, J.S., Rogueda, P.G.A., Crooks, E.R., Pitt, A.R., Simister, E.A., “Dynamic surface tensions of nonionic surfactant solutions”, J. Colloid Interf. Sci.,188(2), 423-430(1997).

15 Xu, S., Damodaran, S., “Kinetics of adsorption of proteins at theair/water interface from a binary mixture”, L angmuir,10(2), 472-480 (1994).

16 MacLeod, C.A., Radke, C.J., “Chage effects in the transient adsorption of ionic surfactant at fluid interfaces”, Langmuir,10(10), 3555-3566 (1994).

17 Joos, P., Fang, J.P., Serrien, G., “Comments on some dynamic surface tension measurements by the dynamic bubble pressure method”, J. Colloid Interf. Sci.,151(1), 144-149 (1992).

18 Borwankar, R.P., Wasen, D.T., “The kinetics of adsorption of ionic surfactants at gas-liquid surfaces”, Chem. Eng. Sci.,41, 199-201 (1986).

19 Bonfillon, A., Langevin, D., “Viscoelasticity of monolayer at oil/water interfaces”, Lan gmuir,9(8), 2172-2177 (1993).

20 Chang, C.H., Franses, E.I, “Modified Langmuir-Hinselwood kinetics for dynamic adsorption of surfactants at air/water interface”, Colloids and S urfaces,69, 189-201 (1992).

21 Jeong, J.B., Kim, J.Y., Kim, H.C., “Dynamic surface tension and its diffusional decay of dodecyl ethoxylates with different homologue distribution”, J. Colloid Interf. Sci.,250(2), 496-502 (2002).

22 Mak, C., Cornu, E., Moresoli, C., Chen, P., “Surface tension, diffusion and kinetics studies of an air-stripping process”, Sep. Purif. Technol.,36(2), 95-106 (2004).

23 Liu, J.J., Li, P.L., Li, C.M., Wang, Y.M., “Diffusion-controlled adsorption kinetics of aqueous micellar solution at air/solution interface”, Colloid & Polymer Sci.,287(9), 1083-1088 (2009).

24 Ritacco, H., Langevin, D., Diamant, H., Andelman, D., “Dynamic surface tension of aqueous solutions of ionic surfactants: Role of electrostatics”, Langmuir,27(3), 1009-1014 (2011).

10.1016/S1004-9541(13)60562-5

2012-03-19, accepted 2012-08-06.

* To whom correspondence should be addressed. E-mail: liujunji@tju.edu.cn