Diffusion and Reaction Model of Catalyst Pellets for Fischer-Tropsch Synthesis

Wu Jianmin; Sun Qiwen; Zhang Zongsen; Pang Lifeng

(Yankuang Energy R&D Co., Ltd., State Key Laboratory of Coal Liquefaction and Coal Chemical Technology, Shanghai 201203)

Diffusion and Reaction Model of Catalyst Pellets for Fischer-Tropsch Synthesis

Wu Jianmin; Sun Qiwen; Zhang Zongsen; Pang Lifeng

(Yankuang Energy R&D Co., Ltd., State Key Laboratory of Coal Liquefaction and Coal Chemical Technology, Shanghai 201203)

The diffusion and reaction phenomenon in a Fe-based catalyst pellet for Fischer-Tropsch synthesis was studied. It was considered that the pores of catalyst pellets were full of liquid wax under Fischer-Tropsch synthesis conditions. The reactants diffused from the bulk gas phase to the external surface of the pellet, and then the reactants diffused through the wax inside the pellet and reacted on the internal surface formed along the pore passages of the pellet. On the basis of reaction kinetics and doubleα-ASF product distribution model, a diffusion and reaction model of catalyst pellet was established. The effects of diffusion and reaction interaction in a catalyst pellet, the bulk temperature, the reaction pressure and the pellet size on the reactivity were further investigated. The relationship between the internal diffusion effectiveness factor of spherical catalyst pellet and the Thiele modulus were also discussed. The bulk temperature and pellet size have significant effects on the reactivity, while the pressure shows only a slight influence on the reactivity. The internal diffusion effectiveness factor decreases with an increasing Thiele modulus.

Fischer-Tropsch synthesis; diffusion and reaction; catalyst pellet; internal diffusion effectiveness factor

1 Introduction

The Fischer-Tropsch synthesis (FTS) process, which converts syngas to paraffins, olefins and oxygenates, is believed to be one of the most important options for the production of clean transportation fuels and chemical feedstocks amid the circumstances of depleting crude oil resources today[1–4]. The FTS products consist of a complex multicomponent mixture of linear and branched hydrocarbons and oxygenated products, the majority of which are linear hydrocarbons[5].

Although a lot of researches have been conducted in the course of the development of Fischer-Tropsch technology, information concerning detailed descriptions of the diffusion and reaction behaviors at the pellet level, which is of great importance for reactor scale-up and catalyst development, is relatively few in the literature so far, because of the inherent complexity of FTS system. Intra-pellet diffusion and reaction interaction behavior have a great effect on heterogeneous catalytic reaction characteristics, catalyst performance execution and reactor capability. Elucidating catalytic reaction behavior of internal particle and realizing the effect of transfer and reaction factors on the reaction outcome will provide theoretical basis for catalyst design and reactor scale-up. Hence, with respect to the complex Fischer-Tropsch synthesis reaction system, the study on pellet level model is of great significance.

In order to describe the diffusion and reaction behavior and its effect on reactivity, it is of paramount importance to combine a FTS kinetics model and carbon chain growth probability model with the diffusion-reaction model for catalyst pellets. The FTS kinetics has extensively been studied, and many attempts have been made on the rate equations describing the FTS reactions[6]. Meanwhile, the hydrocarbon products were lumped according to the carbon number of hydrocarbon molecules with an ideal Anderson-Schulz-Flory (ASF) distribution (a single parameter,α) other than twoαvalues of chain growth probability distribution. Hence, twoαvalues of chain growth probability based on double active sites theory over the Fe-based catalyst will be worth further applying in the pellet model established in this study.

More recently, Madon, et al.[7]have put forward a comprehensive study on the diffusion and reaction process in Co and Ru-based catalyst pellets, leading to an olefin re-adsorption model. Yang, et al.[8]have investigated the mass transfer limitations on fixed-bed Fischer-Tropsch synthesis. Wang, et al.[9]also have established a comprehensive millimeter level catalyst pellet model with detailed mechanistic kinetics in FTS. However, all of these studies on pellet models were focused on the millimeter level catalyst pellet, and seldom models dealt with detailed description of the diffusion and reaction behaviors at the micron level pellets in the literature.

Therefore, the main objective of this work is to establish a comprehensive micron level catalyst pellet model for the complex Fischer-Tropsch synthesis system, into which the mechanistic kinetics model and the two α values of chain growth probability (doubleα-ASF distribution model) based on the Fe-based catalyst in FTS are imbedded. The multicomponent diffusion-reaction model is then applied to analyze the interaction between diffusion and reaction theoretically and to simultaneously discuss the influence of bulk temperature, reaction pressure and pellet size on reaction outcome for Fischer-Tropsch synthesis at the micron level pellets.

2 Establishment of Catalyst Pellet Model

2.1 Fe-based Fischer-Tropsch synthesis catalyst

Precipitated Fe-based catalysts (Fe-Cu-K2O) were developed by Yankuang Energy R&D Co., Ltd. Characteristic parameters of the Fe-based catalyst are listed in Table 1.

Table 1 Characteristic parameters of Fe-based catalyst for Fischer-Tropsch synthesis

2.2 Fischer-Tropsch synthesis reaction

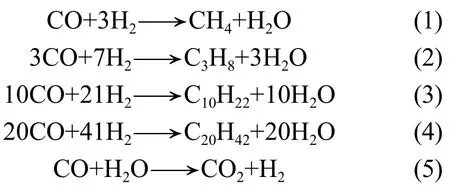
In the Fischer-Tropsch synthesis system there exist CO, H2, CH4, lower hydrocarbons, oil, wax, H2O, CO2, and oxygenated compounds due to the high complexity of synthesis reaction. To simplify the process, it is not necessary to take into account non-dominant products. Water gas shift reaction is indispensable for the iron based catalyst. According to the lumped thought, CH4, C3H8, C10H22, C20H42, CO2and H2O are regarded as main products in this study[11]. Hence, the following reactions are deemed to be independent reactions by lumped thought. CO is chosen as the key component.

2.3 Mathematical description of pellet diffusion and reaction model

For a spherical catalyst pellet in which multiple reactions occur, the dimensionless forms (r=R/Rp) of mass and energy balances at steady state can be expressed by the following differential equations[12]:

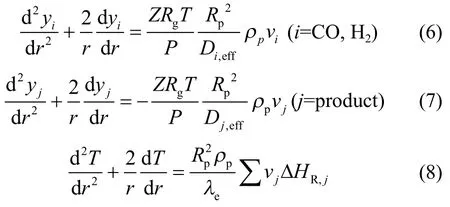
with the corresponding boundary conditions shown below:

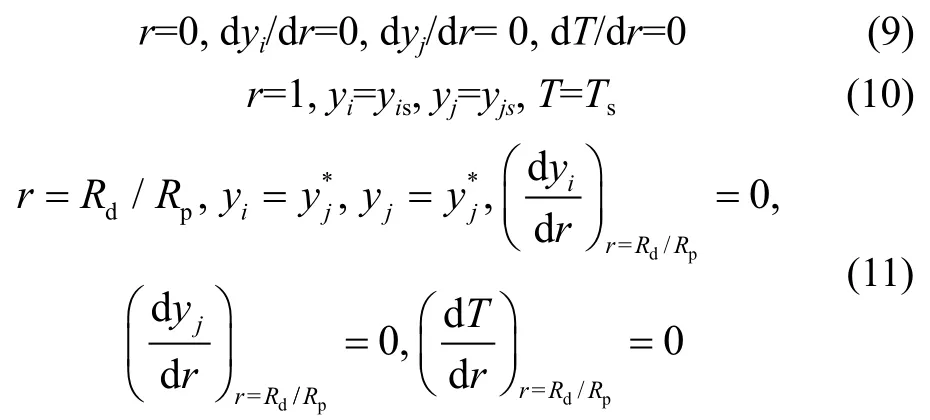
It should be noted that, for the catalyst pellet simulation, the internal diffusion effectiveness factor on the basis of component can be calculated from:

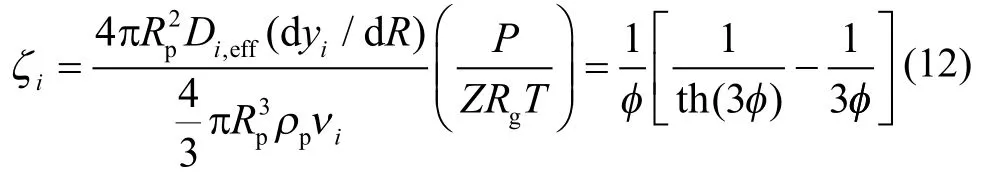
3 Kinetics and Physicochemical Properties

3.1 Reaction kinetics equations and product distribution model

The reaction rate of CO was approximately expressed as the sum of hydrocarbon formation rate and CO2formation rate (WGS reaction rate). Hence, the reaction rate of CO based on precipitated Fe-based catalyst used in this study can be written as[13-14]:

In this work the carbon number distribution of Fischer-Tropsch products on Fe-based catalyst was studied by a modified Anderson Schulz Flory distribution with twoαvalues of chain growth probabilitiy[5]. Then the twoα-ASF distribution expression becomes:

The expressions forα1,α2andβbased on hydrocarbons with carbon numbersn＞2 can be found in the literature[15-16]. C1and C2products do not obey the doubleα-ASF distribution. So W1and W2can be calculated from the literature[16]. All of the parameters in the kinetics model and the twoα-ASF distribution model are derived from the low temperature Fischer-Tropsch synthesis research report of Yankuang Energy R&D Co., Ltd.

3.2 Physical and chemical properties

3.2.1 Effective diffusivity prediction

The diffusivities of CO, H2and CO2in the liquid solvent, wax, can be calculated from the following correlations[17]:

Because the direct experimental data are not available for the other relevant components, their molecular diffusivities in the liquid wax are, by means of diffusivity correlations in infinitely dilute solutions, estimated according to the following equation[18]:

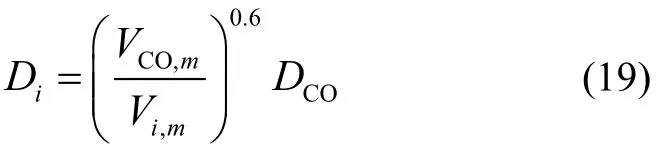
The mole volumeVi,mcan be calculated by the Tyn-Calus method[18]. The corresponding effective diffusivity of componentiin the catalyst pores is calculated by correcting the molecular diffusivity with the porosity and tortuosity.

The tortuosity can be estimated according to the Hugo correlation[19]:

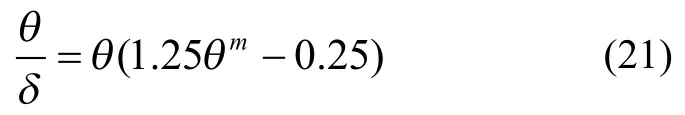
where parametermis 1.0 generally.

3.2.2 Effective thermal conductivity prediction

The effective thermal conductivity of catalyst pellet can be estimated according to the Woodside random distribution heat transfer model[20]:

in which the thermal conductivity of liquid (λL) is calculated by the Latini method[21]. The thermal conductivity of catalyst (λS) may refer to the thermal conductivity of Fe3C based on the cognition and study of iron carbide activity phase for Fischer-Tropsch synthesis[10].

3.2.3 Enthalpy difference

By neglecting that the enthalpy variation effect of the reactant solubility balances with that of product evaporation, the overall enthalpy difference can then be approximated by the formula[18,22]:

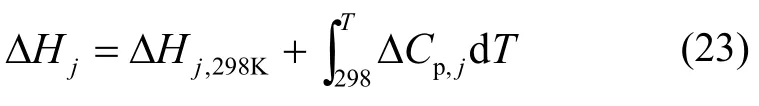
4 Simulation and Discussion

The model Equations (6—8) together with the boundary conditions given by Equations (9—11) lead to a twopoint boundary-value problem (BVP). The solution of the boundary value problem by applying standard orthogonalcollocation method[23]can be transformed into the solution of a set of nonlinear algebraic equations realized by employing the Broyden method[24].

4.1 Intrapellet concentration and temperature profiles

It is of significance to investigate the interaction between diffusion and reaction in a Fischer-Tropsch synthesis catalyst pellet, which is rather complex compared to cases related with simple reactions. Simulation was carried out for the Fischer-Tropsch synthesis under the condition ofP=2.1 MPa,T=513 K, and H2/CO (mole ratio)=1.65 with the initial concentration of the key components equating toyCO=0.3738,yH2=0.6168,yCO2=0.0037,yH2O=0, andyCH4=0.0005, respectively. Figures 1 and 2 show the concentration profiles of key components and temperature profile in wax-filled catalyst pores under the Fischer-Tropsch synthesis condition. As shown in Figures 1 and 2, the Fischer-Tropsch synthesis reaction mainly occurred at the external shell of catalyst pellet according to the concentration gradients of CO and H2. At the reaction sites, the concentrations of CO and H2decreased quickly, while the concentrations of hydrocarbons increased remarkably.

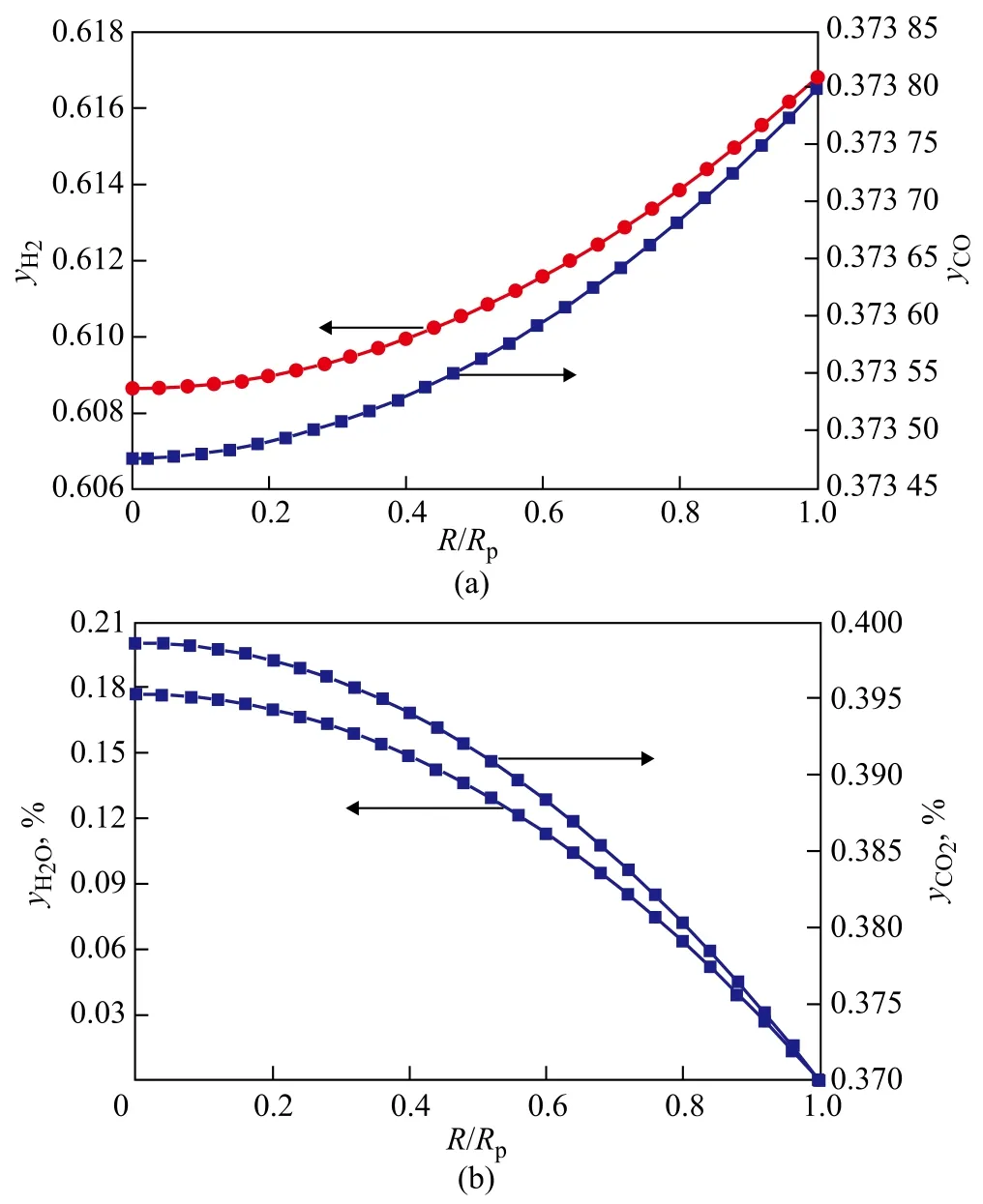
Figure 1 Concentration profiles of key components in catalyst pellet

Figure 2 Concentration profiles of hydrocarbons and temperature profile in catalyst pellet

The reason is that CO is consumed not only by the FTS reaction, but also by the WGS reaction, leading to the rap-id consumption of CO. Because the hydrocarbon-forming reactions generally prevail in the Fischer-Tropsch synthesis system, it is not surprising that the concentration of the accompanying product, H2O, exhibits a steadily increasing trend along the whole pellet dimension. The relatively high liquid concentration of H2O means that the WGS reaction will emerge gradually from a startup state to a fully developed state.

Judging from the concentration profiles of components, it can be concluded that the concentrations of methane and C10H22were higher than C3H8in the catalyst pellet based on chain growth characteristic of FTS because of the high H2concentration. Meanwhile, the trend of increase in CO2concentration proceeds relatively slowly at this site because of the reversible WGS reaction. The molecules of relatively higher hydrocarbons (C5+) tended to form in the low temperature FTS catalyst pellet. The temperature difference between the center of pellet and the pellet surface was equal to 0.012 ℃ due to high exothermic reaction and extremely small pellet diameter.

Based on the analysis of the concentration profiles, there is almost no intra-pellet diffusion restriction in the catalyst pellet, especially pertaining to the reactant CO. As it is described in the reference[13], the phase equilibrium ensures that liquid phase fugacities of CO and H2throughout the pellet are equal to their corresponding gas pressure outside the pellet. As a result, the surface fugacities are constant throughout the pellet partial pressures of CO and H2, and under these conditions synthesis reactions are unaffected by the presence of intra-pellet liquids.

The internal diffusion effectiveness factors (ζ) of CO and H2are 0.999 05 and 0.999 66, respectively, which are nearly equal to 1. Hence, the CO concentration rarely influences diffusion rates and in this case the Fischer-Tropsch synthesis reaction is controlled by dynamics.

4.2 Temperature effect on reactivity

The temperature effect on the concentration profiles of components and the temperature difference between the external surface and the center of the pellet are shown in Figures 3 and 4.

It can be seen from these figures that, with the bulk temperature increasing from 503 K to 523 K, the decrease in CO and H2concentrations becomes faster, because the diffusion rates of reactants gradually decreases to a small extend. A slight trend of increase in CH4, C3H8and C10H22concentrations appears with an increasing temperature, while the CH4concentration increases to a greater extent. These changes indicate that the increase of bulk temperature suppresses the chain growth probability of hydrocarbons, while the CH4selectivity increases. The reason is that WGS reaction enhances the involvement of carbon source of converted CO with an increasing temperature and, accordingly, decreases the carbon source of hydrocarbon-forming reaction. On the other word, it is not good for carbon chain growth with an increasing bulk temperature. The temperature difference between the external surface and the center of the pellet is small and keeps a slowly increasing trend with an increasing bulk temperature. This phenomenon originates not only from small reaction rate at relatively low temperature but is also caused by the micron level pellet diameter.

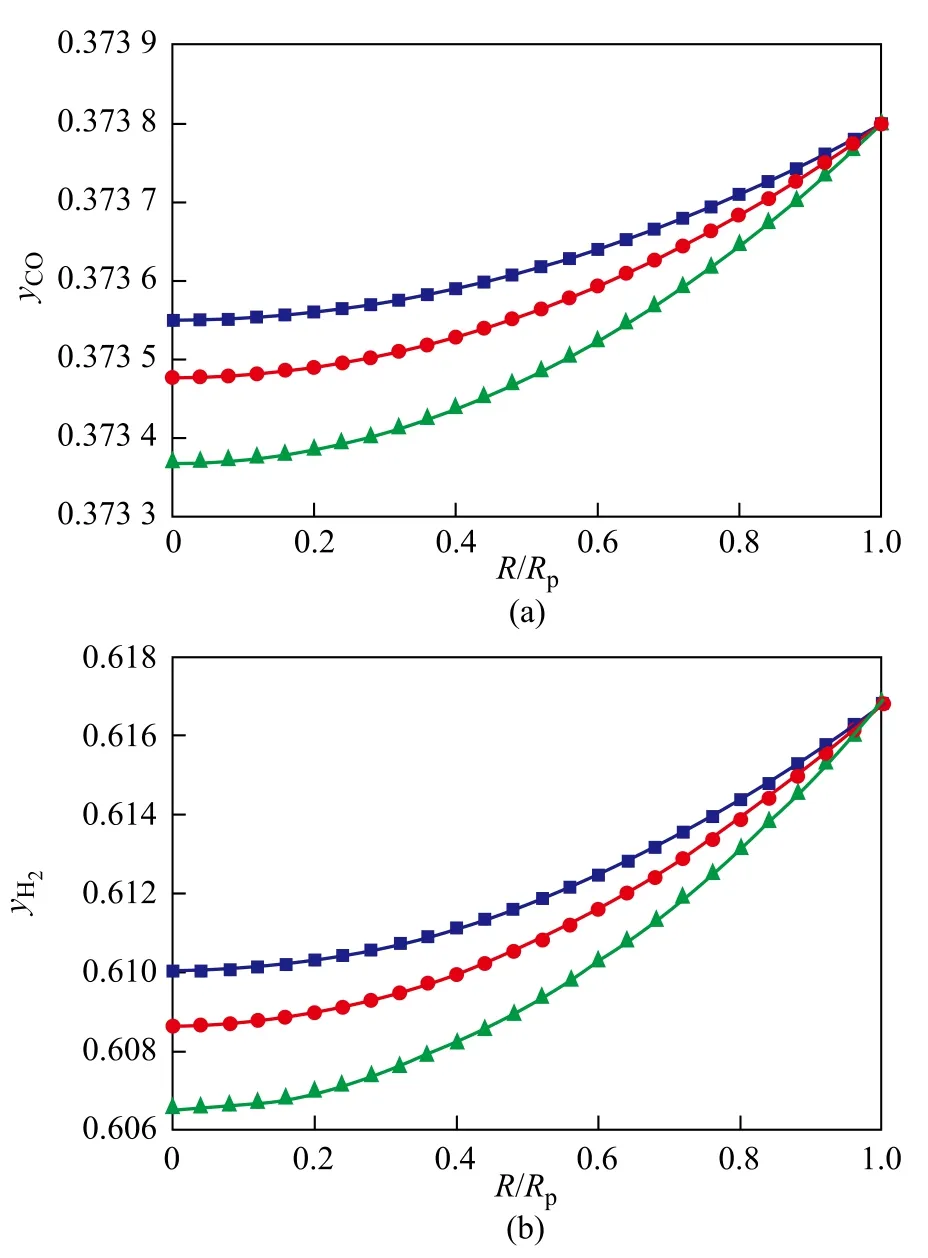
Figure 3 Temperature effect on the concentration profiles of key components in catalyst pellet (P=2.1 MPa, H2/CO=1.65, Rp=60μm)

It can be found from these results that low temperature is more favorable for suppressing the selectivity of the undesired products (CH4and CO2). In addition, an optimalselectivity of C2+ products can be achieved by properly selecting the operating temperature.

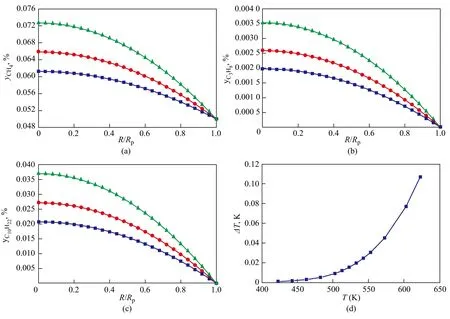
Figure 4 Temperature effect on the concentration profiles of hydrocarbons and temperature difference in catalyst pellet (P=2.1 MPa, H2/CO=1.65, Rp=60μm)

4.3 Pressure effect on reactivity

The pressure effect on the concentration profiles of components and the temperature difference between the external surface and the center of the pellet are shown in Figures 5 and 6. Figures 5 and 6 indicate that the reaction pressure imposes only a slight influence on the reactivity, mainly because of the small effect of pressure on the diffusivities of the reactants in the waxy products. The variation of the temperature difference between the external surface and the center of the pellet with the pressure shows a corresponding trend in the case of the temperature difference variation with the bulk temperature.

Figure 5 Pressure effect on the concentration profiles of key components in catalyst pellet (T=513 K, H2/CO=1.65, Rp=60μm)

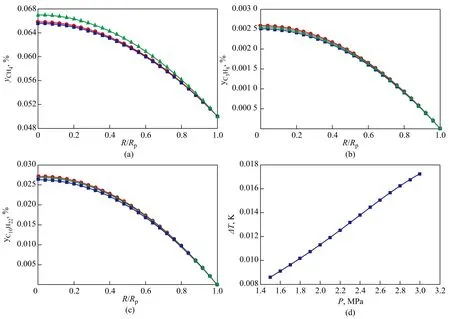
Figure 6 Pressure effect on the concentration profiles of hydrocarbons and temperature difference in catalyst pellet

4.4 Pellet size effect on reactivity

The pellet size effect on the concentration profiles of components and the temperature difference between the external surface and the center of the pellet are shown in Figures 7 and 8.

It can clearly be seen that for a very small catalyst pellet the internal temperature of pellet increases and concentrations of CO and H2decrease with an increasing pellet size owing to the increase in diffusion resistance. It can be seen from the hydrocarbon concentration profiles that the magnitude of increase in concentration of the undesired products in the catalyst pore, CH4, is greater than the increase of C2+ products concentrations with an increasing pellet size, which shows that smaller catalyst pellet is desirable for decreasing the diffusion resistance of reactants and products through the catalyst. The temperature difference between the external surface and the center of the pellet increases with an increasing pellet size because of the increase of reaction heat amount. According to the reactivity analysis, it can be deduced that the large catalystpellet size plays a negative role in improving the reactivity of desired products because of strong diffusion effects. To enhance the reactivity, small catalyst pellets are preferred. For the micron level catalyst pellet, the internal diffusion effectiveness factor always stays at a high level, so the reaction environments of the internal region and the surface of pellet are almost the same. However, for the millimeter level catalyst pellet with diameter ranging from around 2 mm to 4 mm, the internal diffusion effectiveness factor is within a range of 0.14—0.28[15], which corresponds to a condition of severe diffusion restriction. Hence, very small catalyst particles should be used in FTS intrinsic kinetic experiments if liquid wax is present in the pellet pores.

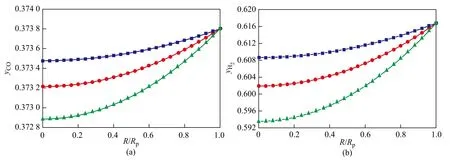
Figure 7 Pellet size effect on the concentration profiles of key components in catalyst pellet (T=513 K, P=2.1 MPa, H2/CO=1.65)

Figure 8 Pellet size effect on the concentration profiles of key components in catalyst pellet (T=513 K, P=2.1 MPa, H2/CO=1.65)

In a word, it is clear that small diameter catalyst pellet should be applied in the slurry Fischer-Tropsch synthesis reactor. For the fixed-bed Fischer-Tropsch synthesis reactor, a proper pellet size (at millimeter level) can maintain a low pressure drop in the reactor and provide effective heat removal.

4.5 Internal diffusion effectiveness factors of spherical catalyst pellet

According to Equation (12), the relationship between the internal diffusion effectiveness factor (ζ) of spherical catalyst pellet and the Thiele modulusis shown in Figure 9.

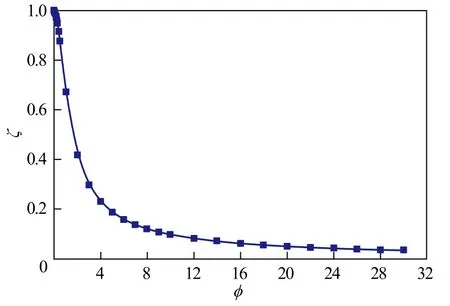
Figure 9 Relationship between the internal diffusion effectiveness factor of spherical catalyst pellet and Thiele modulus

The criterion for assessing the transport restriction is shown below[25]:

It can be seen that the internal diffusion effectiveness factor approximates to 1 when the Thiele modulus is lower than 0.4, which indicates that diffusion in spherical pelletmoves quickly and the effect of internal diffusion can be ignored. When the Thiele modulus is lower than 2 and greater than 0.5, the internal diffusion effectiveness factor is between 0.4 and 0.9, which shows that the effect of internal diffusion is obvious. When the Thiele modulus is greater than 2, the internal diffusion effectiveness factor is very small, which corresponds to a condition of severe diffusion restriction. The trend of the internal diffusion effectiveness factor decreases with a slow increase in the Thiele modulus.

5 Conclusions

On the basis of reaction kinetics and doubleα-ASF product distribution model, a catalyst pellet model is developed and shown to be a reasonable description of diffusion and reaction phenomena in a Fe-based Fischer-Tropsch synthesis catalyst pellet. Orthogonal collocation and the Broyden method are used to solve the pellet model equations. The concentration profiles of key components and hydrocarbons and temperature profile in the pellet pores are obtained. The simulation results show that intra-pellet diffusion restrictions almost do not exist in the pellet pore and the internal diffusion effectiveness factors (ζ) of CO and H2are 0.999 05 and 0.999 66, nearly equal to 1, respectively.

The effects of bulk temperature, reaction pressure and pellet size on reactivity in the catalyst pellet are also simulated. The study results show that the hydrocarbons chain growth probabilities are suppressed with an increasing bulk temperature, while the CH4concentration increases to a greater extent. The rate of decrease in CO and H2concentrations becomes faster because the diffusion resistance of reactants gradually increases to a smaller extent. Furthermore, the temperature difference between the external surface and the center of the pellet is small, and, however, still maintains a trend of slow increase. The effect of pressure on reactivity is not remarkable. With an increasing pellet size, the internal temperature of pellet increases coupled with a decrease in the concentration of CO and H2. The increase of CH4concentration is much greater than the concentration of C2+ hydrocarbon products. The temperature difference between the external surface and the center of the pellet increases with an increasing pellet size. Small catalyst pellets are responsible for the enhanced reactivity. The internal diffusion effectiveness factor decreases with an increasing Thiele modulus. Acknowledgement: Financial support from the National Basic Research Program of China (973 Program, 2010CB736203) is gratefully acknowledged.

Nomenclature

dR—cell shell thickness, μm

m—correlation parameter

n—amount of substance, mol

P—pressure, MPa

R—the distance from the centre in the catalyst, μm

ν—reaction rate, mol/(g·s)

T—temperature, K

V—gas volume, m3

y—mole fraction

Z—compressibility factor

Greek Symbols

β—mole fraction of organic product synthesized on site 1

Subscripts

g—gas

i, j—component

L—liquid

n—number of carbon

[1] Sie S T, Senden M M G, Van Wechem H M H. Conversion of natural gas to transportation fuels via the Shell middle distillate synthesis process [J]. Catalysis Today, 1991, 8(3): 371-394

[2] Dry M E. Present and future applications of the Fischer-Tropsch process [J]. Applied Catalysis A: General, 2004, 276(1/2): 1-3

[3] Dry M E. The Fischer-Tropsch process—Commercial aspects [J]. Catalysis Today, 1990, 6 (3): 183-206

[4] Schulz H. Short history and present trends of Fischer-Tropsch synthesis [J]. Applied Catalysis A: General, 1999, 186(1/2): 3-12

[5] Dry M E. High quality diesel via the Fischer-Tropsch process—A review [J]. Journal of Chemical Technology and Biotechnology, 2001, 77(1): 43-50

[6] Van der Laan G P, Beenackers A A C M. Kinetics and selectivity of the Fischer–Tropsch synthesis: A literature review [J]. Catalysis Reviews-Science Engineering, 1999, 41(3/4): 255-318

[7] Madon R J, Iglesia E. Hydrogen and CO intrapellet diffusion effects in ruthenium-catalyzed hydrocarbon synthesis [J]. Journal of Catalysis, 1994, 149(2): 428-437

[8] Yang J H, Kim H J, Chun D H, et al. Mass transfer limitations on fixed-bed reactor for Fischer-Tropsch synthesis [J]. Fuel Processing Technology, 2010, 91(3): 285-289

[9] Wang Y N, Xu Y Y, Xiang H W, et al. Modeling of catalyst pellets for Fischer-Tropsch synthesis [J]. Industrial & Engineering Chemistry Research, 2001, 40(20): 4324-4335

[10] Ma Q F. Practical Thermophysical Properties Manual [M]. Beijing: Agriculture and Mechanical Press of China, 1986 (in Chinese)

[11] Wu J M, Zhang H T, Ying W Y, et al. Simulation and analysis of a tubular fixed-bed Fischer-Tropsch synthesis reactor with Co-based catalyst [J]. Chemical Engineering & Technology, 2010, 33(7): 1083-1092

[12] Zhu B C. Chemical Reaction Engineering, [M]. 4th ed. Beijing: Chemical Industry Press, 2006 (in Chinese)

[13] Van der Laan G P, Beenackers A A C M. Intrinsic kinetics of the gas-solid Fisher-Tropsch and water gas shift reactions over a precipitated iron catalyst [J]. Applied Catalysis A: General, 2000, 193(1/2): 39-53

[14] Lox E S, Froment G F. Kinetics of the Fischer-Tropsch reaction on a precipitated promoted iron catalyst. 2. Kinetic modeling [J]. Industrial & Engineering Chemistry Research, 1993, 32(1): 71-82

[15] Huff Jr G A, Satterfield C N. Evidence for two chain growth probabilities on iron catalysts in Fischer-Tropsch synthesis [J]. Journal of Catalysis, 1984, 85(2): 370-379

[16] Kuipers E W, Vinkenburg I H, Oosterbeek H. Chain length dependence ofα-olefin readsorption in Fischer-Tropsch synthesis [J]. Journal of Catalysis, 1995, 152(1): 137-146

[17] Wang Y N. Modelization and simulation of fixed-bed Fischer-Tropsch synthesis: Kinetics, pellet and reactor [D]. Taiyuan: Institute of Coal Chemistry, Chinese Academy of Sciences, 2001 (in Chinese)

[18] Poling B E, Prausnitz J M, O’Connell J P. The Properties of Gases and Liquids [M]. 5th ed. New York : McGraw-Hill, 2005

[19] Hugo P. Der Einfluß der Porenvernetzung auf den Labyrinth-Faktor von Preßlingen und Sinterkörpern [J]. Chemie Ingenieur Technik, 1974, 46(15): 645-646

[20] Woodside W, Messmer J H. Thermal conductivity of porous media.Ⅰ. Unconsolidated sands [J]. Journal of Applied Physics, 1962, 32(9): 1688-1699

[21] Latini G, Passerini G, Polonara F. A Prediction method for thermal conductivity of alternative refrigerants in the liquid phase [J]. International Journal of Thermophysics, 1996, 17(1): 85-98

[22] Wu J M, Sun Q W, Gao T F, et al. Thermodynamic calculation and analysis of Fischer-Tropsch synthesis system [J]. Chemical Engineering, 2012, 40(3): 30-34 (in Chinese)

[23] Finlayson B A. Nonlinear Analysis in Chemical Engineering [M]. New York: McGraw-Hill, 1980

[24] Broyden C G. A class of methods for solving nonlinear simultaneous equations [J]. Mathematics of Computation, 1965, 19(92): 577-593

[25] Gonoz E E, Gottifredi J C. Rational approximations of effectiveness factor and general diagnostic criteria for heat and mass transport limitations [J]. Catalysis Reviews-Science Engineering, 1983, 25 (1): 119-140

Recieved date: 2013-06-17; Accepted date: 2013-07-18.

Sun Qiwen, E-mail: yetech@ye-tech. com.