Ⅰ-Ⅱ混合型应力强度因子分析的三角形 Williams单元★

徐 华 刘文祥

(广西大学土木建筑工程学院 工程防灾与结构安全教育部重点实验室，广西南宁 530004)

工程结构中不可避免地含有类似裂纹的缺陷存在，并且以Ⅰ-Ⅱ混合型裂纹最为常见。为了分析这些裂纹缺陷对工程结构安全性的影响，通常将应力强度因子作为重要的研究参量。因其与裂纹体几何构形、外荷载等因素密切相关，难以直接测得，往往采用数值方法获得。

随着大型计算机计算能力的增强，有限元方法得到了广泛的应用，并且在工程结构分析中具有较强的适应性。早在19世纪60年代，Swedllow和Kabayashi等利用常规有限元获得裂尖应力强度因子，但该方法需加密裂尖区离散网格，即需大量的自由度，才能使应力强度因子达到一定的精度［1］，为了减少计算工作量，Levy，Tracey，Hellen 和 Akin 等［2］分别提出了几类代表性的奇异元。由于这些奇异元存在缺乏刚性位移与常规元不易协调等不足之处，后来 Henshell［3］和 Barsoum［4］分别独立提出了 1/4 边中结点奇异等参元克服了这一缺陷，这种单元网格可以划分的相当粗，就能满足工程精度要求，但计算结果受人为主观因素影响较大。Williams［5］以裂尖为极点建立局部坐标系，推导了以级数形式表示的位移场和应力场，这是断裂力学中的第一个局部解，基于此，Cheung［6］和 Leung［7］分别利用 Williams 级数建立了有限条模型和二层分型有限元模型进行结构断裂分析，杨绿峰等［8，9］建立了断裂分析的Williams单元。

文献［8，9］中忽略了裂尖微三角的影响，且只对纯Ⅰ型和Ⅱ型问题进行了研究，本文在此基础上，建立了Ⅰ-Ⅱ混合型裂纹裂尖应力强度因子分析的三角形Williams单元，该单元很好的克服了裂尖奇异性问题，且单元的位移模型中含有与应力强度因子直接相关的参数，可以直接确定应力强度因子。

1 裂尖奇异区离散方式和奇异区位移场

对于含裂纹的弹性体，围绕裂尖O确定应力奇异域(如图1所示)，其外围是常规区域，利用普通有限元法进行离散、分析。以裂尖O为中心用一组射线沿转角方向将奇异域离散为多个扇形条元。任取其中的一个扇形条元OAB作为典型单元，说明奇异域单元分析过程:首先利用一组环绕裂尖O且相互平行的折线(记为Γ1，Γ2，…，Γn)，进一步将扇形条元离散为一组几何形状相似的梯形单元和一个三角形微子域OCD，其中任意两相邻折线Γi+1，Γi到裂尖 O 的距离之比为常数 α，α∈(0，1)，分别称 n，α 为奇异区径向离散数和径向离散比例因子。

图1 裂尖附近区域离散单元示意图

利用Williams级数，建立Ⅰ-Ⅱ混合型裂纹裂尖区整体位移场:

其中，u0，v0为裂尖位移;ai，bi中 i=1，2，…;m 为待定系数，且a1，b1分别与应力强度因子KⅠ和KⅡ有关;对于平面应变问题，式中系数κ=3－4μ;对于平面应力问题，系数κ=(3－μ)/(1+μ)。

根据式(1)定义的位移场，可以在求得位移模型中的待定参数ai，bi后，利用系数a1，b1得到裂尖应力强度因子:

裂尖奇异区典型单元OAB划分的n+1个微单元包括:裂尖三角形微单元ODC、最外层的过渡微单元ABFE以及梯形CDEF中的n－1个梯形微单元，如图1所示。随着n的增大，直线CD逐渐逼近裂尖O，但不能到达。因此文中将考虑裂尖微三角ODC对总刚的贡献。

梯形CDEF包含有n－1个自相似的梯形微单元，对于其中的任意微单元e，根据普通有限元理论建立单元位移场{u}e，或称为局部位移场，且有:

由于局部位移场必须与总体位移场相协调，所以可以将微单元e的全部节点(本文采用八节点四边形单元)坐标依次代入单元OAB的总体位移场表达式(1)中，求得:

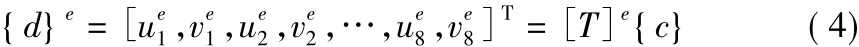
式(4)将微单元位移场的节点位移用总体位移场的待定参数表示出来，矩阵［T］e称为位移场转换矩阵，且有:

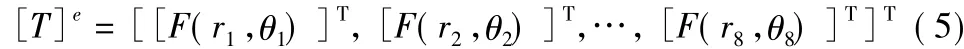
这里，(ri，θi)为微单元 e的节点 i(i=1，2，…，8)在坐标系Oxy中的极坐标。

将式(4)代入式(3)，可得:

式(6)表示的单元位移场中节点参数{c}不局限于特定的物理意义。

2 奇异区三角形Williams单元刚度方程

1)梯形CDAB的刚度方程。梯形CDAB包括过渡单元ABFE和梯形条元集合EFCD，分别形成两块区域的控制方程后叠加，即可得到该区域的刚度方程，具体推导过程可仿照文献［8，9］，这里不再赘述。现考虑裂纹面不受外力的情况，形成梯形CDAB的刚度方程为:

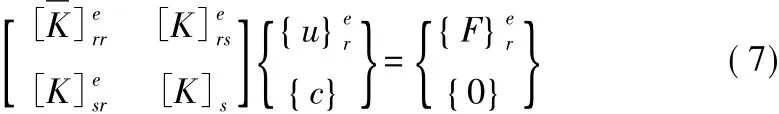
其中，分块刚度矩阵的下标r，s分别表示位于常规区和奇异区的节点;上划线表示常规区单元刚度分块矩阵。

2)微单元OCD的广义参数刚度方程。

三角形OAB的第n+1层单元紧邻裂尖O，建立六节点三角形广义参数单元位移场:

其中，［T(n+1)］为三角形单元转换矩阵，且有:

其中，(ri，θi)，i=1，2，…，6，表示三角形微单元六个节点的极坐标。

所以，三角形单元的广义参数刚度方程为:

其中:

集合梯形单元CDAB和裂尖三角形ODC的刚度方程，容易形成OAB的广义参数刚度方程，可以分块表示为:

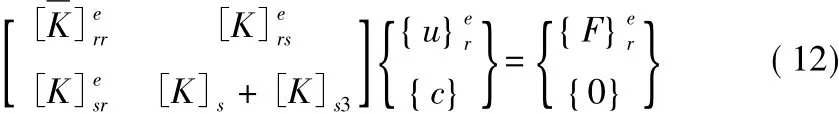
式(12)即为三角形Williams单元OAB的刚度方程。集合求解域内全部离散单元的刚度方程可以形成结构总体刚度方程。在该方程中引入边界条件并求解，即可根据式(2)直接求得应力强度因子KⅠ和KⅡ。

3 算例分析

带有一条中心斜裂纹的弹性有限宽板，一端固定，其余端自由，其中裂纹长度 2a=0.10 m，板宽2w=1.0 m，板高 h=1.25 m，裂纹倾斜角为γ，在y轴方向受到均布拉力σ=30.0 kN/m。弹性模量 E=2 ×105MPa，泊松比 μ =0.167，板厚 t=0.01 m，如图 2 所示。利用本文建立的混合型裂纹分析的广义参数三角形Williams单元求解裂纹尖端处KⅠ和KⅡ，并与文献［2］给出的解析解作比较。

图2 带中心斜裂纹弹性板

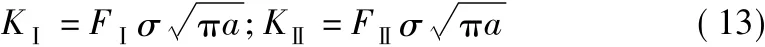
其中，FⅠ和FⅡ是关于裂纹倾角及a/w的函数，可以通过边界配置法求得或者直接通过文献［2］第348～349页查得。这里三角形 Williams单元的重要参数取值［8，9］分别为:m=10，α =0.9，n=300。

表1列出了倾斜角 γ 分别取30°，45°，60°和75°时应力强度因子KⅠ和KⅡ的计算值，并与文献［2］的结果进行比较。

表1 应力强度因子与裂纹倾斜角的关系

表1列出了本文方法和解析法计算应力强度因子KⅠ和KⅡ的结果，可以看出，两种方法的结果基本吻合，最大误差不超过0.8%，证明三角形Williams单元具有很高的计算精度。另外，图3给出了三角形Williams单元所得应力强度因子与倾斜角γ的关系曲线，由图可见，裂纹倾斜角γ在第一象限内时，KⅠ和KⅡ随γ的增加而呈现不同的变化规律，前者逐渐减小，后者表现出先增后减的规律。

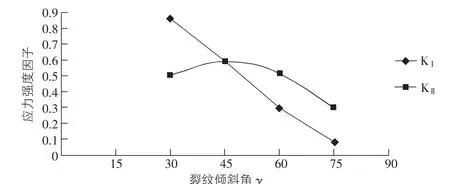
图3 KⅠ和KⅡ随着γ变化

4 结语

本文利用Williams级数，研究建立了Ⅰ-Ⅱ混合型裂纹应力强度因子分析的广义参数三角形William单元。算例分析表明:对于含中心裂纹单向拉伸板，三角形Williams单元计算结果与应力强度因子手册中提供的解析解吻合较好，随着倾斜角γ的增加，KⅠ逐渐减小，KⅡ表现为先增后减，与实际相符。三角形Willams单元原理简单，便于构造和应用，具有较高的计算精度和计算效率。

［1］黄观鸿，杜家吉.混合型应力强度因子KⅠ、KⅡ的有限元计算［J］.天津大学学报，1982(1):25-37.

［2］中国航空研究院.应力强度因子手册(增订版)［M］.北京:科学出版社，1993.

［3］R.D.Henshell，K.G.Shaw.Crack tip finite elements are unnecessary［J］.International Journal for Numerical Methods in Engineering，1975(9):495-507.

［4］R.S.Barsoum.On the use of isoparametric finite elements in linear fracture mechanics［J］.International Journal for Numerical Methods in Engineering，1976(10):25-37.

［5］M.L.Williams.On the stress distribution at the base of a stationary crack［J］.Journal of Applied Mechanics，1957(24):109-114.

［6］C.W.Woo，Y.H.Wang，Y.K.Cheung.The mixed mode problems for the cracks emanating from a circular hole in a finite plate［J］.Engineering Fracture Mechanics，1989，32(2):279-288.

［7］A.Y.T.Leung，R.K.L.Su.Mixed-mode two-dimensional crack problem by fractal two level finite element method［J］.Engineering Fracture Mechanics，1995，51(6):889-895.

［8］杨绿峰，徐 华，李 冉，等.广义参数有限元法计算应力强度因子［J］.工程力学，2009，26(3):48-54.

［9］杨绿峰，徐 华，彭 俚，等.断裂问题分析的Williams广义参数单元［J］.计算力学学报，2009，26(1):33-39.