钢－混凝土混合梁接合面受力分析

陈琦

(福建信息职业技术学院，福建福州 350012)

主跨为钢梁，边跨(或部分伸入主跨)为混凝土梁的结构形式常出现在大跨度斜拉桥(如日本生口桥、法国诺曼底桥、武汉白沙洲长江大桥)和悬索桥(如佛山平胜大桥、福州鼓山大桥)中.该类桥梁由于主跨采用钢梁，跨度可以较大，边跨的混凝土梁起到很好的锚固作用且建造成本低［1］.钢－混接合段应保证钢梁和混凝土梁之间刚度过渡的匀顺性和力传递的顺畅性，是其设计的关键技术之一.但是，由于采用钢和混凝土两种不同性质的材料，钢混接合段的截面刚度有较大突变，受力状态复杂，应力集中程度高［2－5］.

钢－混接合段基本上都是由钢箱梁、混凝土梁和剪力钉三个部分组成，目前国内外主要有四种构造形式，每种形式各有优缺［6］.由于混凝土在钢箱梁基础上进行浇注，钢与混凝土间发生相对滑动之前，存在水泥凝胶体和钢板接触面之间的化学胶结力以及粗糙不平的钢板表面和混凝土之间的机械咬合力，当剪力超过粘结力时，接触面发生相对滑移，剪力才由钢与混凝土之间摩阻力和剪力钉来承受.在接合面设计中，一般忽略粘结力、机械咬合力及钢混接合面的接触效应，认为剪力由剪力钉均匀承受.这样的假定，对于整体结构的受力而言，影响是可以忽略的，但接合面的摩擦力在剪力传递中起的作用，以及剪力在剪力钉群中的分布，对剪力钉的布置均产生影响.因此，对钢混接合面进行分析，研究接触摩擦应力对接合面受力的影响以及剪力在剪力钉群中的分布，对于钢－混接合段剪力钉的设计具有重要意义.

1 非线性接触

钢－混接合段两接触面是紧压密贴关系，应采用非线性接触有限元方法进行分析.接触问题是一种高度非线性行为，接触物体不可相互侵入，当表面发生接触时，在接触面之间一般传递切向力和法向力.本文采用ABAQUS［7］中面－面接触非线性(刚体－柔体接触)，选用IDCOUP3R作为面－面接触单元，以混凝土梁端承压面为主面(刚性面)，钢梁端承压板为从面(柔性面)，主从面之间采用“硬”接触(即主从面间隙为0时，从属面上的节点不能侵入主控面，主从面分离时，接触解除)，主从面发生滑动时采用小滑动接触算法，切向力采用库伦摩擦模型.库伦摩擦是用来描述接触面之间相互作用的摩擦模型，应用摩擦系数μ来表征在2个表面之间的摩擦行为，该模型中接触面剪应力达到一个临界值前，切向运动一直为0，而临界剪应力取决于法向接触压力即τcrit=μP(P是两表面间的接触压力)，直到接触面间的剪应力等于摩擦剪应力的极限值μP时，接触表面才会滑动(相对滑动)，同时摩擦力的数值不能超过材料的抗剪强度［8－10］.

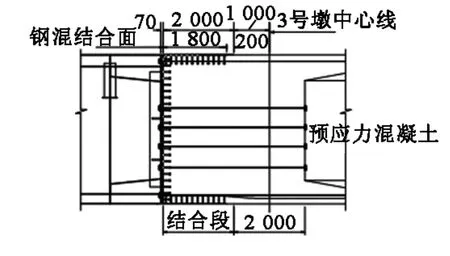
图1 大桥钢－混接合段(单位:mm)Fig.1 Steel－ concrete joining section(unit:mm)

2 工程背景

某大桥为一座独塔自锚式悬索桥，主跨为钢箱梁(150 m+235 m)，其他梁段为混凝土箱梁.该桥的混凝土梁体伸入主跨一部分，钢混接合面在桥墩附近.过渡段钢箱梁顶板厚14 mm，底板厚12 mm，采用“U”肋上“T”型加劲式加强，横梁腹板、隔板及内外纵腹板厚均为16 mm;钢箱梁顶板和底板均深入混凝土梁1 800 mm，设有剪力钉与混凝土连接，在深入混凝土1 200 mm且与内外纵腹板对应处设有底板支撑板.北岸接合段混凝土梁体端部为400 cm厚的混凝土实体(除中部有4个直径为100 cm的过人孔外)，钢梁和混凝土梁间设厚度为70 mm的钢板作为承压板，通过剪力钉和纵向预应力与混凝土梁连接.钢－混接合段结构构造如图1.

选用该桥北岸钢混接合段进行分析，分析区域尺寸:纵桥向×横桥向×竖向=17.5 m×42 m×3.5 m，模型分析区域及荷载布置如图2所示，荷载条件见表1.

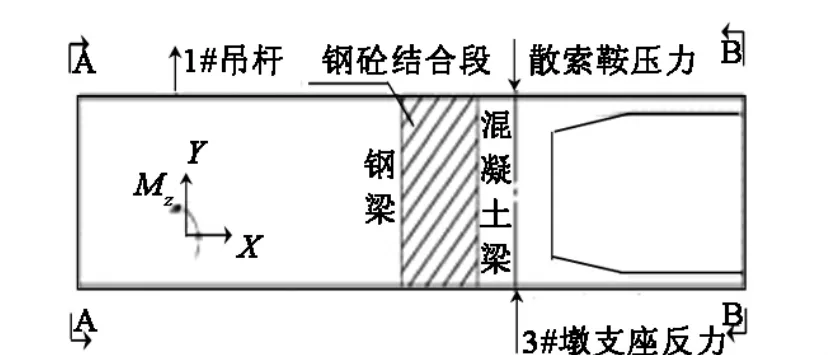
图2 分析区域及荷载布置图Fig.2 Analysis zone and load arrangement

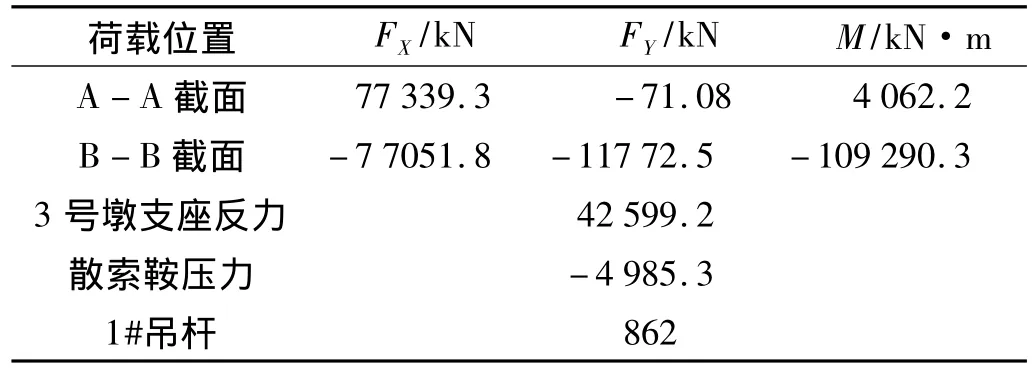
表1 荷载条件Tab.1 Load condition

3 模型的建立

采用通用大型有限元程序ABAQUS建模，计算模型除没有考虑横桥向坡度的影响外，其余均按实际尺寸建模.混凝土均采用实体单元，分为两个部分，钢与混凝土接合段形状规则，采用六面体单元C3D8R，混凝土箱梁形状不规则，采用四面体C3D4.钢箱梁部分采用壳单元，根据板件规格与单元划分的难易，采用了S4R、S3R、Stri65、S8R单元.剪力钉采用同尺寸的梁单元B31，剪力钉的一端节点与端承板贴在一起，剪力钉(除与端承板相连的节点外)采用imbed埋在接合段的混凝土中;施加荷载的垫板采用刚度无穷大实体刚性单元;钢端承板与混凝土间设置刚性接触单元IDCOUP3R.模型共有80 588个单元.

钢材采用Q345，容重为78.5 kN·m－3，弹性模量为2.06×105MPa，泊松比为0.3;混凝土采用C50，混凝土容重为26 kN·m－3，弹性模量为3.45×104MPa，泊松比为0.2.为了便于分析，将B－B截面设为固定端，荷载考虑了成桥状态的设计荷载，包括A－A截面的轴力、剪力、弯矩，支座反力，吊杆轴力，聚索点的压力以及模型的自重.假设分析区梁节段结构为均质弹性体，对模型进行弹性分析.

为了探讨接触摩擦应力对接合段受力的影响，建立三个模型:一是钢－混接合面建立面－面接触单元，但摩擦系数为0，同时不考虑预应力的影响;模型二假定接触面为标准的单向接触(摩擦系数为0.6)，仍不考虑预应力的影响;模型三既考虑摩擦影响也设置预应力筋.

4 计算结果分析

4.1 接触面

图3给出了模型1混凝土梁端接合面法向压应力分布情况.从图3可知，在上下面板以及加劲肋附近压应力较大，远离这些板件地方，压应力很小，甚至为0.这是因为自锚式悬索桥的梁受到较大的压力，而钢－混结合段一般选在弯矩较小处，梁作为压弯构件，但仍全截面受压.在接合面上，纵向压力通过上下面板和加劲肋传给端承板，由于钢箱梁端承板厚度方向刚度有限，在与上下面板和加劲肋连接处附近与混凝土箱梁充分接触，而远离这些板件地方甚至没有接触上.从图3可知，接触面上最大法向压应力为3.69 MPa，没有超过混凝土抗压强度设计值，模型2的法向压应力与模型1几乎相同，模型3稍大(模型3中由于预应力产生的预压力与桥梁产生的压力具有数量级上差距，故对接触面上压应力影响不大).可见，该桥主梁轴向压力在接合面传递是有效的.

图3 模型1钢－混接触面压应力Fig.3 Pressure stress of steel－ concrete interface in model 1

图4给出了模型3混凝土梁端接合面竖向剪应力分布情况(模型1、2也基本相同)，由图4可知:上下面板附近的剪力大，中部小(除个别预应力施加点)，这主要是因为上下面板附近的压应力大(见图3)，剪应力也大.从接触面上的摩擦力合力来看，模型2为62.32 kN，占该截面总剪力的3.31%;模型3为63.96 kN，占该截面总剪力的3.39%.可见，接触面上的摩擦阻力承担了部分截面剪力的传递，降低了剪力键的剪力.但在本工程中，由于接合面受压且变形较小，所以摩擦力承担的剪力比例较小.

图4 模型3钢－混接触面剪应力Fig.4 Pressure stress of steel－ concrete interface in model 3

图5给出了模型3混凝土梁端接合面上的粘结滑移状态(模型1、2也基本相同).从图5可知:上下面板附近出现较大的黏住区域，中部出现较大的滑移甚至脱离的区域，这主要是因为上下缘均设置预应力且上下钢面板均伸入混凝土梁，使上下受到压力较大(如图3)，临界剪应力也大，没有发生滑移;中部区域由于压力小和钢板变形，临界剪应力也小，发生滑移甚至脱离.从接合面的最大滑移量来看，三个模型均较小，模型1为0.018 89 mm，模型2为0.019 17 mm，模型3为0.019 1 mm.可见，该连接方式能保证钢与混凝土的可靠连接.

图5 模型3钢－混接触面滑移状态Fig.5 Status of steel－ concrete interface in model 3

4.2 剪力钉

由图6、图7可知，同一列的剪力钉承受的竖向剪力值呈U型分布，也就是接近上下面板的剪力钉比中间的剪力钉承受大得多的剪力.该结论与文献［8］一致.但实际工程中基本上均假定剪力钉均匀受剪.笔者认为:由于强大轴力的存在，钢梁存在垂直轴力方向变形，使剪力钉受剪，随着离中和轴越远，变形越大，剪力钉受到剪力越大，同时竖向剪力较小，所以剪力钉受力仍基本呈U型.

由图6、图7还可以看出，钢－混接合面3种不同的模拟方式，剪力钉内力分布规律基本一致;相比不考虑接触的模型1的计算结果，模型2、3剪力钉内力有所减少，但幅度不大.

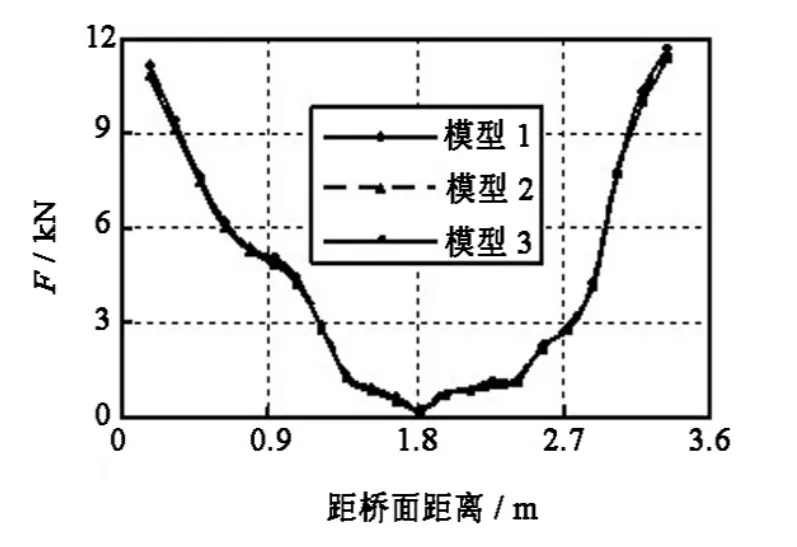
图6 中间列剪力钉剪力分布图Fig.6 Shear of stubs in middle column

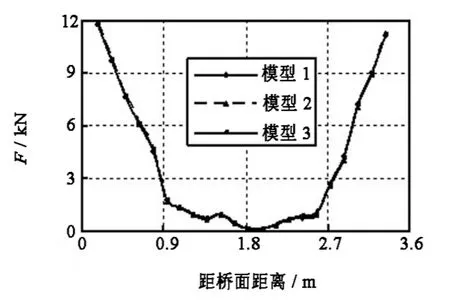
图7 边列剪力钉剪力分布图Fig.7 Shear of stubs in edge column

4.3 钢箱梁

图8给出了模型3的钢箱梁桥面板纵应力分布情况.从图8可知，除翼缘(此处钢与混凝土箱梁刚度相差较大)和吊杆位置处有一定应力梯度外，其余区域应力较为均匀.从图9可知，底板受拉，应力较面板更均匀.可见，接合面刚度过渡较匀顺、传递较顺畅.此外，上下面板均存在剪力滞现象，但不明显，这主要是因为悬索桥的竖向荷载大部分由吊杆传给索，接合面承担的弯矩和剪力不大，而轴向压力较大，起主导作用.

模型1、2底板和面板应力大小、分布规律与模型3基本一致.3个模型中混凝土箱梁受力均匀，分布规律基本相同.可见，是否考虑预应力和接触面摩擦力对混凝土箱梁和钢箱梁受力情况影响不大.

图8 模型3钢箱梁桥面板纵向应力Fig.8 Longitudinal stress of decks of steel box girder in model 3

图9 模型3钢箱梁桥底板纵向应力Fig.9 Longitudinal stress of bottom slab of steel box girder in model 3

5 结论

由于影响钢－混接合面的化学胶结力和机械咬合力的因素很多又缺乏试验数据，其数值难以确定，在分析过程中没有考虑.但通过对钢－混接合段考虑接合面接触摩擦应力的分析，可以得到以下结论:

1)本工程采用的钢混凝土接合段位置、构造形式、传力均较合理，没有明显的应力突变现象.

2)考虑钢－混接合－面接触效应，对钢箱梁和混凝土箱梁的应力分布影响不大，剪力钉内力分布规律基本不变，内力数值有一定的减小.

3)考虑钢－混接合面接触后，接合面的剪力由接触摩擦力和剪力钉共同承受，但摩擦力占的比例较小.

4)由于钢梁存在垂直轴力方向变形，接合面的剪力钉离中和轴越远受到的竖向剪力越大，实际应用中应加以重视.

［1］陈开利，余天庆，习刚.混合梁斜拉桥的发展与展望［J］.桥梁建设，2005(2):1－4.

［2］叶梅新，蒋彪.混合型自锚式悬索桥连接部位传力研究［J］.铁道科学与工程学报，2006，3(6):1－6.

［3］Valente I，Paulo J S.Experimental analysis of perfobond shear connection between steel and lightweight concrete［J］.Journal of Constructional Steel Research，2004，60(3/4/5):465－479.

［4］Fressengeas C，Taupin V，Upadhyay M，et al.Tangential continuity of elastic/plastic curvature and strain at interfaces［J］.International Journal of Solids and Structures，2012，49(18):2 660–2 667.

［5］胡云耀，邵旭东，罗建辉.矩形截面二次预应力组合梁结合面徐变应力分析［J］.工程力学，2011，28(4):89－95.

［6］木曾川桥.揖斐川桥混合结构结合段的设计与施工［J］.预应力混凝土，2001，42(1):37－45.

［7］庄茁，由小川，岑松，等.基于ABAQUS的有限元分析和应用［M］.北京:清华大学出版社，2009.

［8］庄茁，朱万旭，彭文轩，等.预应力结构锚固—接触力学与工程应用［M］.北京:科学出版社，2006.

［9］赵金娟，王世军.双粗糙表面接触模型中微观摩擦系数的确定［J］.西安理工大学学报，2012，28(2):221－223.

［10］胡亚琴.沪崇苏越江大桥索塔锚固区钢混结合面接触分析［J］.中外公路，2008，28(10):174－177.