双轴加载下RC带翼缘剪力墙抗震性能对比分析

史庆轩，王斌，王朋，王南，田建勃

(西安建筑科技大学土木工程学院，陕西西安 710055)

0 引言

建筑师们通常喜欢将矩形墙组合成T型、I型、C型和L型等截面.然而，这种墙肢组合通常导致墙体各部分(腹板与翼缘)之间复杂的相互作用.各方向墙肢独立承担该方向荷载的假设将不再合理.平面外的墙肢作为翼缘，它增加了腹板方向的强度和刚度，也导致了加载方向之间的相互作用.

震害调查及实验研究均表明，双向水平地震较单向地震对结构构件的破坏作用大得多.这是因为一个方向损伤后对其正交方向的抗震能力有较大影响，两个方向的相互耦合作用严重削弱了结构的抗震能力［1］.如果沿两个主轴方向同时施加反复荷载，这两个方向上的强度退化与刚度退化较单方向反复加载严重得多，其延性也有所降低.故研究结构构件在双向力作用下的性能变得尤为重要.

国外对带翼缘剪力墙多维抗震性能的研究已有了一些进展.日本核能安全组织(JNES)［2－3］进行了箱型截面RC剪力墙多轴荷载作用下的模型试验研究，阐明了多轴地震荷载作用对箱型截面带翼缘剪力墙抗震性能的影响.Katrin BEYER［4－5］等人对U型带翼缘剪力墙进行了多维抗震研究，并根据试验结果建立了剪力墙分析模型.而对T型截面的带翼缘剪力墙多维抗震性能国内外却几乎很少研究.所以有必要对这一工程实际中经常用到的剪力墙形式进行研究.

本文基于有限元软件ABAQUS的塑性损伤模型，研究了T形截面带翼缘剪力墙在双向反复荷载作用下的抗震性能，分析比较了其较单轴荷载作用下腹板和翼缘方向各项抗震性能指标的差异，以及个不同双向加载路径的影响.

1 有限元模型的建立

1.1 模型试验概述

基于有限元的数值模拟方法，因其方便、迅速、节省的特点已成为结构构件分析研究的重要手段.但其合理性和可靠性还需模型试验的验证.为此，首先采用大型通用ABAQUS软件模拟了文献［6］中RC剪力墙JLQ－4、JLQ－5的拟静力加载试验，其试验轴压比分别为0.2、0.3.试件截面尺寸如图1，试件高跨比为9.5，剪跨比为2.01.混凝土与钢筋的材料性能列于表1和表2，其中:纵筋采用HRB335级钢筋，边缘配箍均为HRB235级钢筋，混凝土强度等级为C40.

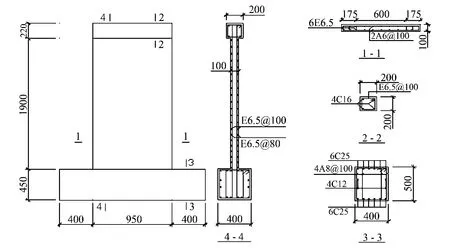
图1 试件几何、截面尺寸与配筋(单位:mm)Fig.1 Dimensions and reinforcement arrangement of speciments(unit:mm)

表1 混凝土材料性能Tab.1 Material properties of concrete

表2 钢筋材料性能Tab.2 Material properties of reinforcement

1.2 有限元模型的建立

采用ABAQUS/Standard模块中的塑性损伤模型模拟混凝土的非线性行为.混凝土拉压本构关系选用《混凝土结构设计规范》［7］条文说明中提供的应力－应变曲线，并在此基础上计算出真实应力和真实应变，即:

式中:σ和ε分别为名义应力和名义应变，即实验测得数据;σture和εture为真实应力和真实应变.进而可换算得到ABAQUS输入时需要的非弹性应变，即:

根据能量等效原理计算出混凝土受拉受压损伤因子，即:

式中:dc和dt为规范给出的应力应变关系中的损伤演化参数;Dc和Dt为在ABAQUS中输入的损伤因子.钢筋的非线性行为采用双折现强化模型，钢筋的初始弹性模量为Es，强化段的弹性模量取为0.01Es.

采用分离式模型进行有限元建模，混凝土单元采用C3D8R，纵筋和箍筋均单元采用T3D2.并将所有钢筋merge成钢筋骨架，通过embedded形式嵌入混凝土单元中，使钢筋与混凝土之间变形协调.墙体与顶部刚性垫梁之间用tie连接，基础梁底面采用ENCASTRE方式约束其底面全部6个自由度.其余各项参数的取值分别为:剪膨角取30o，流动势偏移值取0.1，双轴受压与单轴受压极限强度比取1.16，拉伸子午面与压缩子午面上第二应力不变量的比值取2/3，粘性系数取0.000 5，混凝土受压恢复力系数0.8，混凝土受拉恢复系力数0.2.模拟加载采用与试验相同的加载形式，直至试件的水平承载力下降到最大水平荷载的80%时为止.

1.3 模拟结果对比分析

图2给出了模拟结果与试验结果的荷载－位移滞回曲线对比图.可以看出:模拟结果的峰值荷载、峰值位移、极限荷载、极限位移与试验之间的差异在10%内，故有限元模型对剪力墙的承载力和变形能力能做出较为准确的预测.有限元模拟的滞回曲线没有出现明显的“捏缩”效应，这是因为在ABAQUS模拟中未能考虑混凝土的裂变效应以及钢筋与混凝土之间的粘结滑移，但这一问题对于本课题研究剪力墙骨架曲线的影响甚微.

图2 试验及模拟剪力－顶点位移滞回曲线Fig.2 Experiment and simulation hysteretic curves

图3为模拟结果与试验结果的破坏形态对比图.可以看出，模拟结果已具有相当的精度，因此，建立的模型是有效的.

图3 试件破坏形态Fig.3 Failure mode of the specimen

图4 试件截面尺寸配筋图(单位:mm)Fig.4 Detail section dimensions and reinforcement figure of the specimen(unit:mm)

2 带翼缘剪力墙模型的建立

2.1 模型概述

根据研究需要设计了一T型截面带翼缘剪力墙.墙肢高2.5 m，试件截面尺寸见图4，轴压比为0.3，钢筋与混凝土的材性均采用上述试验所用材料参数，其余参数设定均与之前相同.

2.2 有限元模型建立

采用与上述模拟实验相同的方法建立此带翼缘剪力墙有限元模型，为了便于施加轴力和水平荷载，同时为了防止加载时平面外扭转，在墙肢顶部用tie连接一刚度很大的加载钢板，墙肢底面采用ENCASTRE方式完全约束.

3 模拟结果分析

3.1 加载路径概述

对于多维拟静力加载，由于力控制阶段和位移控制阶段所产生的的轨迹是不同的，为了保证在x－y平面内加载轨迹的一致性，采用位移控制模式加载.选取常用的三种双向加载路径，图5为其加载路径示意图.

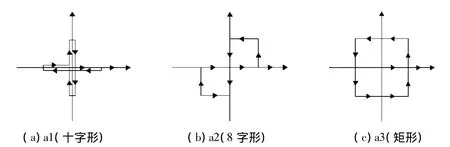
图 5双轴加载路径示意图Fig.5 Schematic diagram of biaxial loading paths

3.2 骨架曲线与滞回曲线分析

图6、图7分别给出了x方向(腹板方向)和y方向(翼缘方向)不同加载路径下模拟结果的骨架曲线，各轴正方向见图4.其中，a0为单轴往复荷载作用下的骨架曲线，a1～a3分别为在上述双轴往复加载路径下的模拟骨架曲线.

图6 不同加载路径下沿腹板方向骨架曲线Fig.6 Skeleton curves along web direction under different loading paths

图7 不同加载路径下沿翼缘方向骨架曲线Fig.7 Skeleton curves along flange direction under different loading paths

可以发现:除x轴反向加载(腹板端部受压时)外，其余方向双轴加载较单轴均表现出明显的双轴耦合效应.在y方向(翼缘方向)循环加载时，腹板位于其中和轴的位置，其承受y方向荷载作用产生的拉压应力很小，未对腹板造成很大的损伤，而x轴反向加载的破坏是由腹板受压区混凝土控制的，所以x轴反向加载未表现出双轴耦合相应.

表3、表4分别列出了单轴和上述三种双轴往复水平荷载作用下x轴正向(翼缘受压方向)及y轴方向的屈服荷载、屈服位移、峰值荷载、峰值位移、极限荷载、极限位移及位移延性系数.因为x轴负向(腹板端部受压方向)未表现出双轴耦合效应，故不对此进行研究.其中:位移延性系数β为试件极限位移Δu与初始屈服位移Δy的比值，极限位移Δu取最大承载力下降10%所对应的墙顶位移;屈服位移采用能量等值法来确定.

表3 不同加载路径下腹板端部受拉方向的特征点信息Tab.3 Characteristic points information of the direction when web end in tension under different loading paths

表4 不同加载路径下翼缘方向的特征点信息Tab.4 Characteristic points information of flange direction under different loading paths

通过骨架曲线和表中计算结果可以发现:在加载初期，单轴和不同双轴荷载作用下的骨架曲线几乎重合，未表现出双轴耦合效应.在达到屈服荷载后，双轴耦合效应逐渐明显，试件的屈服荷载、峰值荷载.极限荷载均小于单轴作用;屈服位移、峰值位移、极限位移也均较单轴提前，位移延性减小.在达到峰值点后，双轴反复荷载作用下试件承载力下降相对单轴更快，强度和刚度退化明显.

3.3 加载路径对比分析

比较三种不同双向加载路径发现:试件的屈服荷载、峰值荷载和极限位移在“8字形”(a2)双轴往复荷载作用下较小.说明双向耦合作用按“十字形”(a1)、“矩形”(a2)、“8字形”(a3)依次增强.

4 结语

经过带翼缘剪力墙抗震性能有限元分析可以得出以下结论:除x轴反向加载(腹板端部受压时)外，其余方向双轴加载较单轴均表现出明显双轴耦合效应，各方向屈服荷载、屈服位移.峰值荷载、峰值位移、极限荷载、极限位移、位移延性系数均减小，强度和刚度退化加剧，其中“8字形”加载路径影响最大.

［1］李宏男，王强，李兵.钢筋混凝土框架柱多维恢复力特性的试验研究［J］.东南大学学报:自然科学版，2002，32(5):728－732.

［2］Habasaki A，Kitada Y，Nishikawa T，et al.Multi－ directional loading test for RC seismic shear walls［C］//The 12th World Conference on Earthquake Engineering.Auckland:［s.n.］，2000:454 －461.

［3］Yoshio Kitada，Takao Nishikawa，Katsuki Takiguchi，et al.Ultimate strength of reinforce concrete shear walls under multi－ axes seismic loads［J］.Nuclear Engineering and Design，2007，237:1 307 －1 314.

［4］Ile N，Reynouard J.Behaviour of U －shaped walls subjected to uniaxial and biaxial cyclic lateral loading［J］.Journal of Earthquake Engineering，2005，9(1):67－94.

［5］Beyer K，Dazio A，Prisetley M J N.Quast－static cyclic tests on U －shaped RC walls test design and preliminary results［C］//The First European Conference on Earthquake Engineering and Seismology.Geneva:［s.n.］，2006:1 －10.

［6］郑山锁，侯丕吉，李磊，等.RC剪力墙地震损伤试验研究［J］.土木工程学报，2012，45(2):51－59.

［7］GB 50010混凝土结构设计规范［S］.北京:中国建筑工业出版社，2010.