消息传递接口环境下等高线简化并行计算适宜性研究

沈 婕，郭立帅，朱 伟，顾乃杰

1.南京师范大学 虚拟地理环境教育部重点实验室，江苏 南京 210046；2.南京师范大学 地理科学学院，江苏 南京 210046；3.中国科学技术大学 计算机科学与技术学院，安徽 合肥 230027

1 引 言

随着网络地图技术的发展及地图应急服务的需要，对实时在线多尺度地理信息服务的需求更加迫切，为了解决海量地理数据实时动态的尺度变换，地图综合的效率需要进一步提高。针对地图综合效率增益方法，学者们提出了建立空间数据索引［1］、构建多尺度空间数据库之间的链接［2－3］、采用渐进式综合策略等方法［4－5］，这些方法虽然能在一定程度上提高地图综合的执行效率，但是传统的硬件串行处理方式已经达到了瓶颈。近年来，基于并行体系结构的硬件资源层出不穷，并行软件也不断发展。在实际的并行机上设计并行程序时，绝大部分采用扩展Fortran和C语言的办法，目前主要有3种扩展的办法：库函数法（MPI、PVM、Cray Craft）、新 语 言 结 构 法（Fortran90、Cray Craft）和编译制导法 （HPF、Cray Craft）。MPI是消息传递模型的一种，便于将串行程序扩展为基于消息传递模型的并行程序，它遵守所有对库函数／过程的调用规则，是为开发基于消息传递模型的并行程序而制定的工业标准，其目的是提高并行程序的可移植性和易用性，用户必须显式地通过发送和接受消息来实现处理器之间的数据交换。MPI具有移植性好、功能强大、效率高等多种优点，几乎所有的并行计算机厂商都提供对它的支持。本文探讨MPI环境下等高线简化的并行计算问题。

并行计算在地学中的应用主要有基于图形处理器（GPU）的通用计算，如文献［6］提出基于多叉树搜索的并行蚁群算法；文献［7］提出基于GPGPU的CUDA架构快速影像匹配并行算法。此外，文献［8］研究了OPEN MP并行计算在卫星重力数据处理中的应用，总之，并行计算在地图综合中的应用还较少。线状要素在地图要素的图形表达和GIS分析中发挥着重要的作用，线要素综合也是地图综合中最重要的方面。等高线是普通地图、数字线划图中重要的表达要素，面向大范围场景下不同尺度的等高线实时表达，对于等高线综合算法的效率提出了要求，本文选择等高线作为地图综合并行计算的研究数据类型。简化是地图综合中最常用的操作，针对简化算法的研究已相对成熟，算法多达数十种，本文拟选取几种典型的简化算法，采用不同数据量的等高线数据，基于MPI的不同并行计算方案，实现其简化并行计算。基于并行计算效率的比较与分析，探讨并行计算中不同简化算法对数据量、计算节点数、通信方式等的适宜性。通过这一研究，为基于MPI的等高线或其他要素地图综合及其他地学高性能计算研究提供借鉴。

2 线要素简化算法效率分析

算法时间复杂度是指算法的时间耗费，是算法中所有语句的频度之和，它是算法所求解问题规模n的函数，用T（n）表示。为了准确地度量算法效率，需要解决两个问题：一个是算法运算次数与问题规模的关系；另一个是问题规模同为n的不同输入实例，即考虑数据分布特征时，应该怎样计算其基本语句的运算次数。本文在分析算法时间复杂度时，先写出算法的伪代码，然后找出其基本语句与问题规模的关系，进而得到算法的时间复杂度。以Douglas－Peucker算法为例，进行阐述。

2.1 Douglas－Peucker算法的思想

Douglas－Peucker算法的基本思想是：先拟定一个阈值D以控制简化的程度，生成一条连接矢量折线首尾节点的直线段，求出线上所有顶点到该直线段的垂直距离，并找到最大距离dmax，比较dmax与阈值D，若dmax＜D，则舍去折线上所有中间点；若dmax＞D，则以dmax对应的点为界，把折线分为两部分，再对这两部分使用上述方法，直到始点和终点之间无点为止。

2.2 Douglas－Peucker算法的伪代码

下面是使用递归实现DP算法的伪代码，D为距离阈值，（i、j为线段的起始点与结束点）：① 寻找到线段pipj距离最远的点pk；② 判断pk到pipj线段的距离与D的关系，如果大于D执行第③ 步，否则执行第④ 步；③ 将线段pipj分为pi到pk与pk到pj两部分，分别使用Douglas－Peucker算法简化；④ 返回简化结果。

2.3 Douglas－Peucker算法的时间复杂度分析

上述代码中第1步的时间复杂度为O（n），而整个算法是通过递归实现的，假设D＜dmax，线段的第m个点将其一分为二，m＞1时，算法执行时间T（n）＝T（m）＋T（n－m＋1）＋O（n），在一定的数据特征下，可能会使得m＝n－m＋1，此时T（n）＝2T（n／2）＋O（n），由主定理［9］可得T（n）＝O（nlogn）；m＝1时，T（n）＝T（1）＋T（n－1）＋O（n），算法的时间复杂度为O（n2）。假设D＞dmax，算法的时间复杂度为O（n）。

2.4 Douglas－Peucker算法的约束参数对其效率的影响分析

Douglas－Peucker算法的约束参数为D（距离阈值），在Ifdistance（pk，pi，pj）＞D这一计算过程中，如果D永大于distance（pk，pi，pj），那么算法的执行次数为n（问题规模），此时算法的时间复杂度为O（n）；如果D永小于distance（pk，pi，pj）就会导致m＝1，算法的时间复杂度为O（n2）。

本文依据上述方法分析了常用的8种线简化算法的时间复杂度及其约束参数对算法效率的影响，发现地图综合算法的效率影响因素不仅依赖问题规模n，还依赖于其约束参数［10］。约束参数对算法效率的影响与算法时间复杂度分析结果在量级上是一致的，这是地图综合算法时间复杂度分析的独有特点。为了探究不同简化算法并行计算适宜性，本研究根据简化算法的时间复杂度将其分为线性与非线性两类，拟选择线性算法Li－Openshaw算法与Circle算法，非线性算法Douglas－Peucker算法与渐进式简化算法进行并行计算试验。综上所述，8种简化算法分析结果如表1所示。

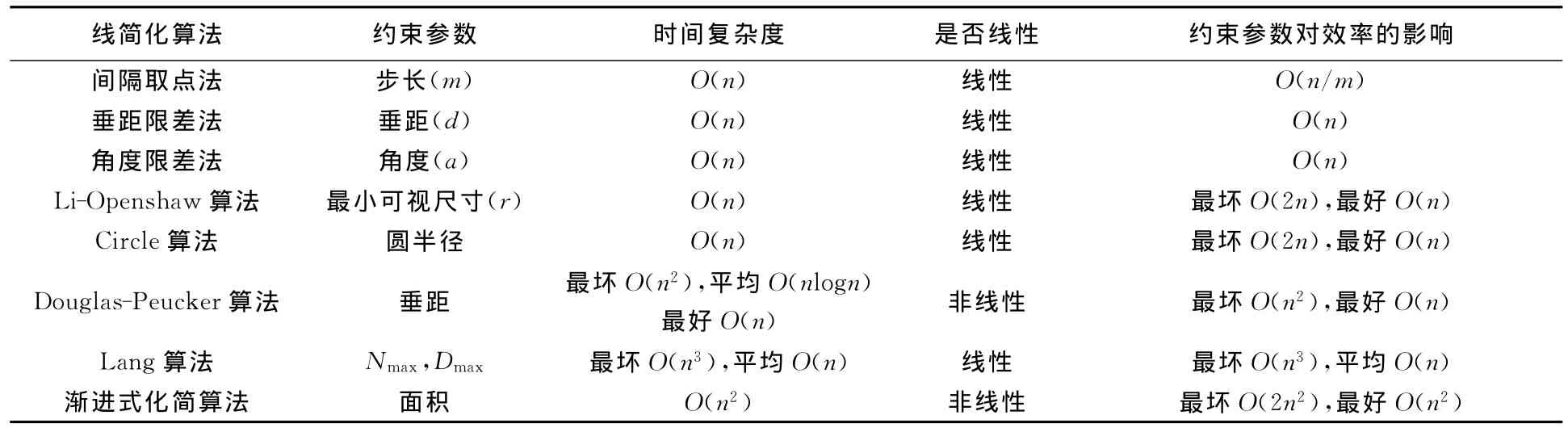
表1 考虑约束参数影响的简化算法时间复杂度Tab.1 Time complexity of simplifying algorithms considering the effect of constraints

3 基于MPI的等高线简化并行计算关键问题

主从模式和对等模式是MPI的两种基本并行计算模式［11］。主从模式中，主节点管理其他计算节点［12］；对等模式中，各个节点地位相同。本文提出的等高线简化并行计算方法以数据划分为基础，更适合主从模式，主节点负责数据划分、发送与合并，计算节点负责等高线的简化计算。基于MPI的等高线简化并行计算由4个过程组成：数据划分、通信、计算和数据合并，其流程如图1所示。

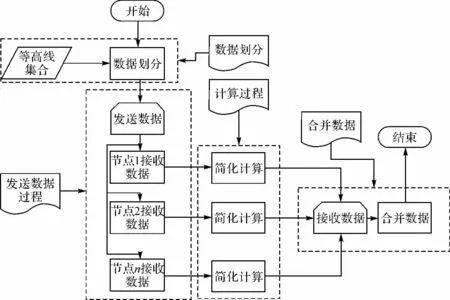
图1 基于MPI的等高线简化并行计算流程图Fig.1 Flow chart of contour simplification parallel computing based on MPI

3.1 数据划分与合并

已有的面向空间数据处理的并行计算方法大多采用规则格网划分或条带划分［13－14］，由于地图综合以处理矢量数据为主，并要求综合前后保持数据的结构特征与拓扑特征，格网划分和条带划分将破坏等高线这种闭合曲线的空间关系，数据合并时开销太大，这种简单划分方法不适合等高线数据。因此，基于矢量数据划分的并行计算，数据划分和合并必须统筹考虑负载均衡与数据分布特征对计算效率的影响。本文提出基于高程带的数据划分方法，基本思想是先根据总数据量及计算节点数目确定每个节点的数据量阈值，将高程相同的等高线合并为一个整体，作为划分基本单元，然后比较其与各节点数据量阈值的关系，将单独或相邻的几个高程带划分成独立的数据块，并且没有打断原有等高线，不同计算节点运算后返回的等高线仍然是闭合曲线，这种划分方法既保证了计算节点的负载均衡，又降低了数据合并的开销。

3.2 通信方式

MPI提供了集合通信和点对点通信两种方式［15］，集合通信要求传输数据量相同，但每条等高线数据量不同，因此本研究采用点对点通信。点对点通信可分为阻塞和非阻塞通信两种类型［16］。阻塞通信发送目标进程立刻需要的数据，必须等到接收数据完成才能执行下一步操作，非阻塞通信可以一边发送数据一边执行计算，将计算与通信重叠。

本研究将比较阻塞和非阻塞通信对等高线简化并行计算效率的影响。等高线简化并行计算在这两种通信方式下的流程如图2所示，阻塞通信方式下，主节点依次发送等高线数据到各计算节点中，计算节点在接收数据完成后开始执行简化计算，如图2（a）所示。非阻塞通信方式下，节点每简化完一条等高线就立即发送，发送操作随即返回，继续处理下一条等高线，进而将计算与通信重叠，如图2（b）所示。

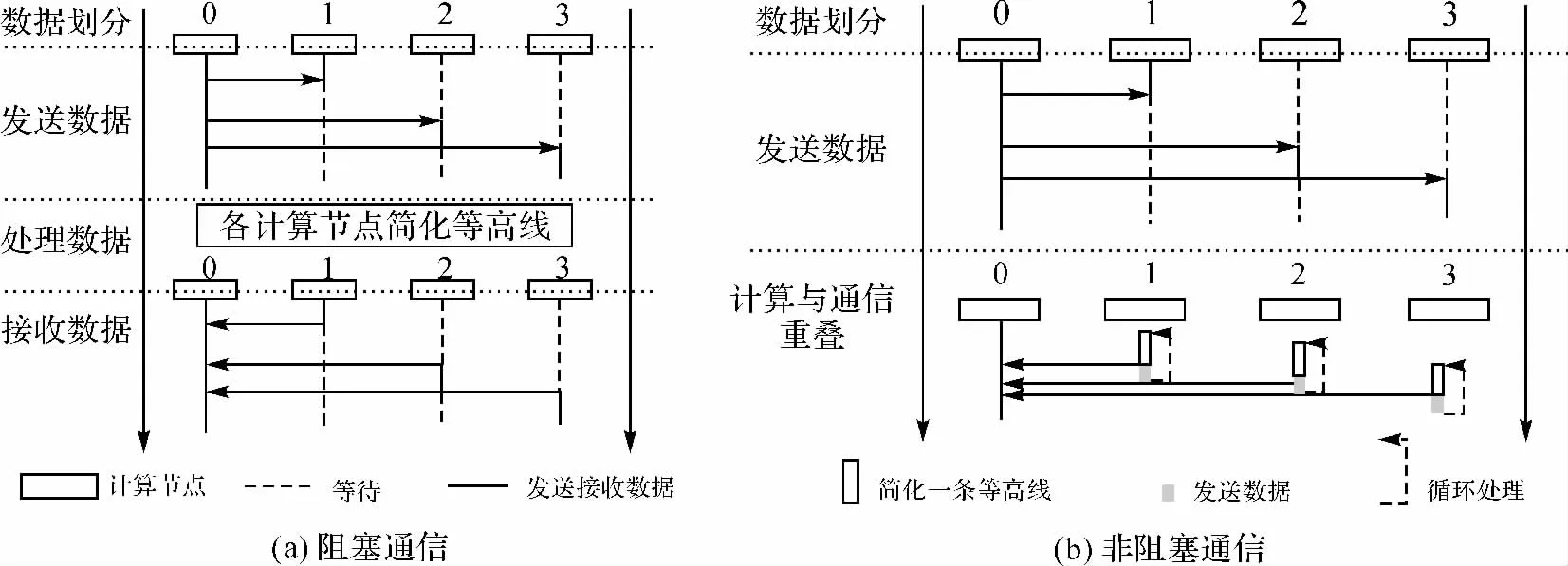
图2 阻塞和非阻塞通信方式下等高线简化并行计算过程Fig.2 Contour simplification parallel computing process under blocking and non－blocking communication

3.3 计算过程

计算过程的执行时间是所有计算节点简化计算执行时间最长的节点所用的计算时间。影响计算过程效率主要有3个因素：数据负载量、简化算法效率和处理任务提交顺序。其中简化算法与数据负载量是确定因素，为了提高并行计算效率，应该改进处理任务的提交顺序［17］。本研究根据划分后数据块的数据量进行降序排序，然后依次发送，以达到数据量大的任务首先执行，进而缩短整个并行计算过程的处理时间。

4 试 验

本试验是在6台计算机组成的小型集群系统中进行，每台计算机的配置为：Inter（R）Core（TM）Quad CPUQ8200＠2.33GHz四核，2GB内存。编程环境为 Visual Studio 2010、GDAL1.4.2和MPICH 1.2.1。试验中使用的等高线数据来源于1∶100万中国陆地区域等高线数据，为了便于发现等高线简化并行计算效率与数据量的变化规律，对原始等高线数据进行了简化和删除处理，得到中国陆地区域的4份数据量基本呈等差分布的数据，测试数据的数据量如表2所示，均为shapefile格式。这4份数据覆盖范围是一致的，但是等高线数量、每条等高线中点的数量不同，由于全国范围的等高线数据显示过于密集，因此以测试数据4为示例，放大了测试数据4中的某一小块区域，如图3所示。

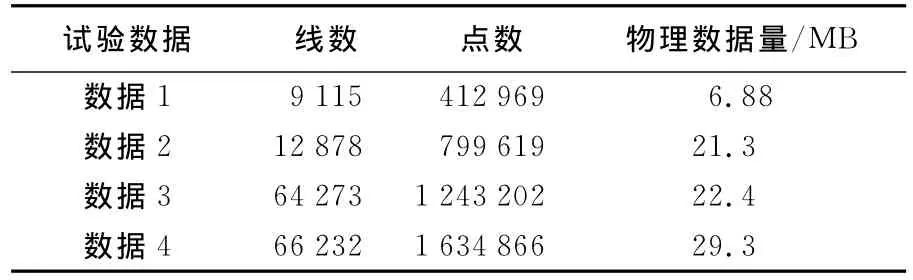
表2 测试数据的数据量Tab.2 The volume of the test data

4.1 约束参数及数据准备

由第2节讨论得知，算法的约束参数对算法效率有影响，本试验中等高线原始比例尺为1∶1 000 000，目标比例尺为1∶4 000 000，选取等高距为500m，根据本试验的数据特征和综合前后的比例尺，试验中各算法的约束参数计算公式如下（O＿Scale为源数据比例尺分母，P＿Scale为目标比例尺分母，SVO为最小可视目标的直径）。

图3 测试数据4的部分放大数据Fig.3 Test data 4and the enlarge of part data

渐进式化简算法：areaTolerence＝0.000 4×0.000 6×pow（P＿Scale，2）／2。

Li－Openshaw 算 法：R＝ （1－O＿Scale／P＿Scale）×SVO×P＿Scale。

Douglas－Peucker算法：D＝0.000 2×P＿Scale。

圆算法：R＝length／（num－1）／2（length为线长度，num为线中点的个数）。

本试验中，将在1、2、4、6个计算节点上执行等高线简化并行计算，为了保证不同计算节点上负载均衡性，基于高程带数据划分思想，将等高线数据分配到不同计算节点上，如表3所示。

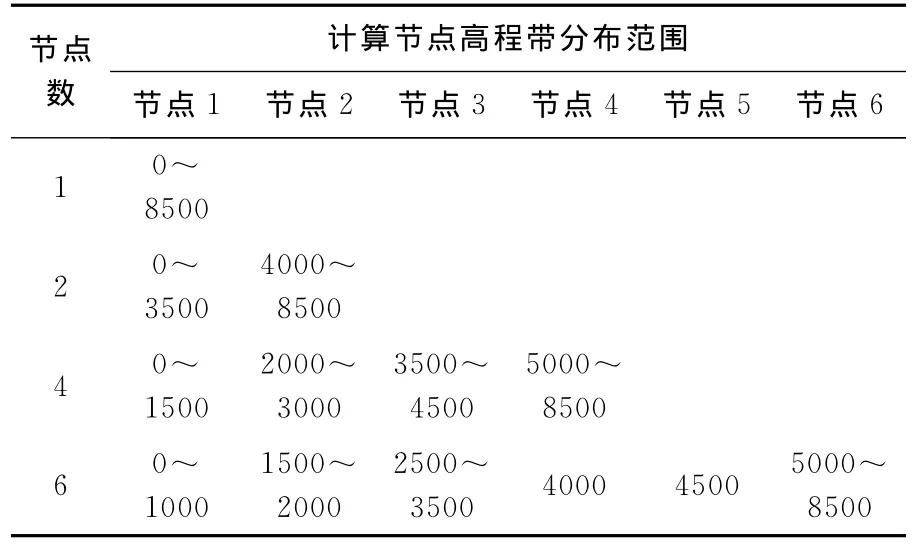
表3 参与计算的不同节点上高程带划分Tab.3 Elevation zones divided on different nodes involved in the calculation m

4.2 试验1：简化算法在串行环境下效率分析

在串行环境下，Douglas－Peucker算法和渐进式简化算法的执行时间与算法的迭代次数有关。虽然Li－OpenShaw和Circle算法都是线性算法，但其原理不同，Li－OpenShaw算法会产生新的数据点，而Circle算法是删除数据中原始的点，其基本语句的复杂度不同。4个简化算法的串行执行时间如图4所示。

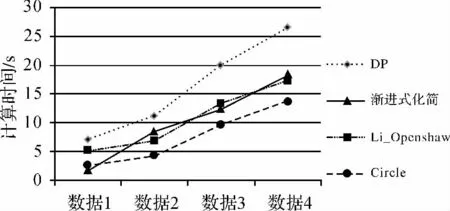
图4 简化算法串行执行时间Fig.4 Serial execution time of simplified algorithm

在当前数据分布特征下，Circle算法执行效率最高；Douglas－Peucker算法的效率较低；渐进式简化算法在数据1时效率最高，其余数据情况下，与 Li－OpenShaw 算法效率相近［18］。通 过分析，可得到以下结论：

（1）算法时间复杂度量级相同，算法的约束参数、数据空间分布特征相近时，算法效率依赖于算法基本语句的复杂度。

（2）算法时间复杂度是度量算法在串行环境下效率的量级，但并不能代表算法执行时的效率，特别是综合算法，影响其执行效率的还有算法的约束参数、数据空间分布特征等。

4.3 试验2：阻塞通信方式下简化算法的并行计算

阻塞通信方式的并行计算是最容易实现的并行计算方法。对于等高线简化并行计算，主节点依次将等高线数据发送到各计算节点，各个计算节点执行简化操作，所有节点都处理完成之后按照阻塞通信方式将处理结果返回给主节点。测试数据的平均阻塞次数如表4所示，简化算法的加速比如图5所示。

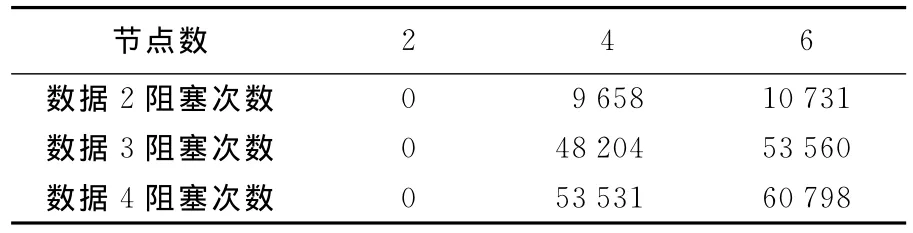
表4 测试数据阻塞次数统计表Tab.4 The blocked count of the test data

分析得到以下结论：

（1）计算节点数为2时，只有一个节点通信，相当于无阻塞，算法效率高。

（2）随着数据量和计算节点的增加，阻塞的次数也相应的增加，算法等待的时间增加，算法效率降低。

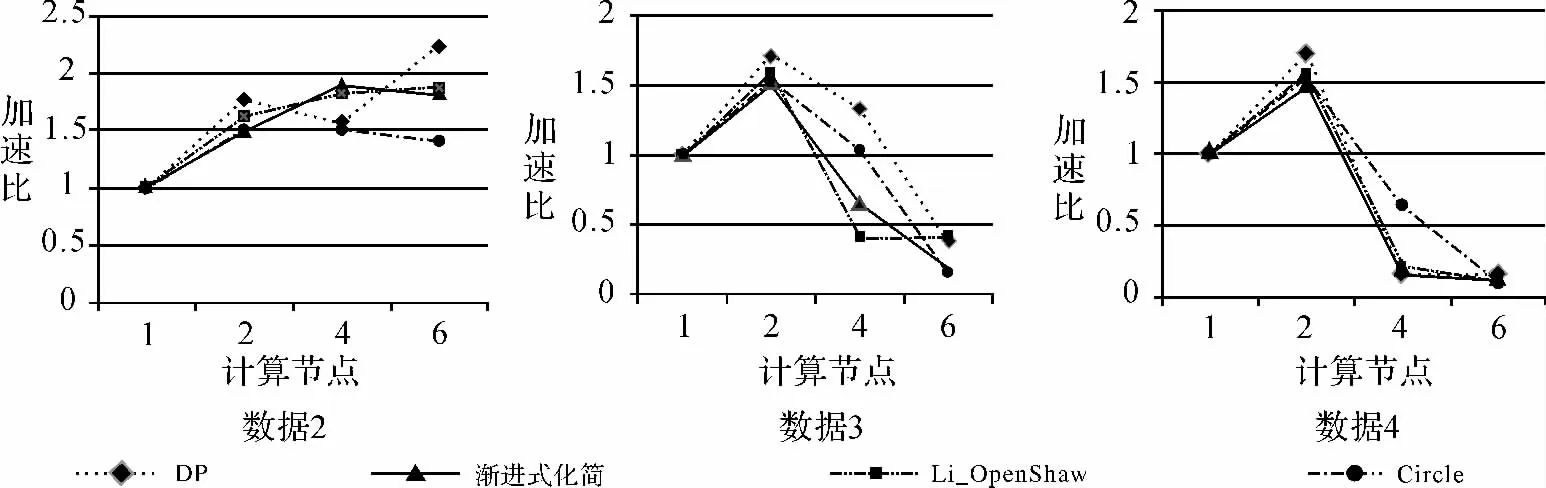
图5 阻塞通信方式简化算法加速比Fig.5 The speedup of the simplified algorithms under the blocking communication

4.4 试验3：不同通信方式下简化算法的并行效率分析

解决因数据量增加而阻塞通信次数增加的办法是使用非阻塞通信，它不必等到通信操作完全完成便可返回。本次试验比较了Douglas－Peucker算法和渐进式简化算法在不同通信方式下处理数据3和数据4的效率，如图6所示。

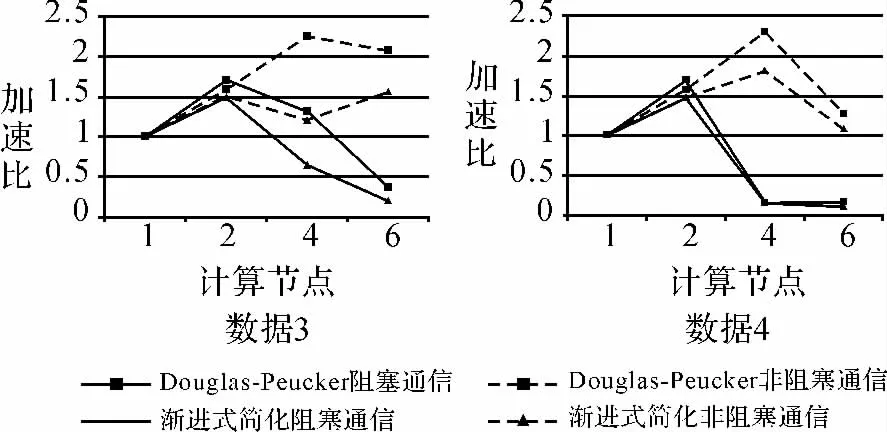
图6 不同通信方式下Douglas－Peucker算法和渐进式简化算法的加速比Fig.6 Speedup of Douglas－Peucker and progessive simplification algorithm under different communications

综合分析可得以下结论：

（1）算法并行计算效率不会随着节点数增加而一直提高。测试数据为数据4时，两个简化算法的加速比峰值都出现于节点数为4的情况下，说明此数据量下，使用4个节点并行计算效率最高。

（2）由图5可知，在阻塞通信方式下，随着节点数的增加，简化算法的效率在降低，甚至可能低于串行的效率。由图6可知，在非阻塞通信方式下，Douglas－Peucker算法和渐进式简化算法的加速比明显高于阻塞通信方式下，算法执行效率更高。在当前数据分布特征下，对于本文所选简化算法，非阻塞通信方式优于阻塞通信方式，更能提高简化算法并行计算的效率。

4.5 试验4：简化结果及其并行适宜性分析

本试验选择了4种数据量的试验数据，其中数据4中的局部数据基于不同简化算法执行并行计算后等高线如图7所示，其中参与计算的节点数为两个，黑色细线为简化前的等高线，红色和黑色粗线为在不同节点上的简化结果。

图7 数据4的局部数据在不同算法条件下的简化结果（粗线）Fig.7 Simplification results of data 4under the conditions of different algorithms（thick line）

此外，由试验2和试验3可知，非阻塞通信方式简化算法的并行效率明显高于阻塞通信方式，因此本试验分析简化算法在非阻塞通信方式下的并行适宜性，图8是4个简化算法在非阻塞通信方式下并行处理测试数据的加速比。通过对图8结果进行分析可以得出以下结论：

（1）算法并行化之后，其效率的变化是不确定的，串行效率高的算法并行效率不一定高。由图4与图8可知，在处理相同数据时，与其他算法相比，Douglas－Peucker算法的串行效率最低，但其并行计算加速比最大，原因是在通信环境、节点数、数据量等因素都相同时，并行计算的通信时间都相同，算法并行后的加速比与其串行执行时间成正比，串行执行时间越长加速比越大。Circle算法和Li－Openshaw算法并行效率不随节点数目增加而增加，随着数据分块数目和数据量的增加，通信开销占用的比例增加，导致效率降低。

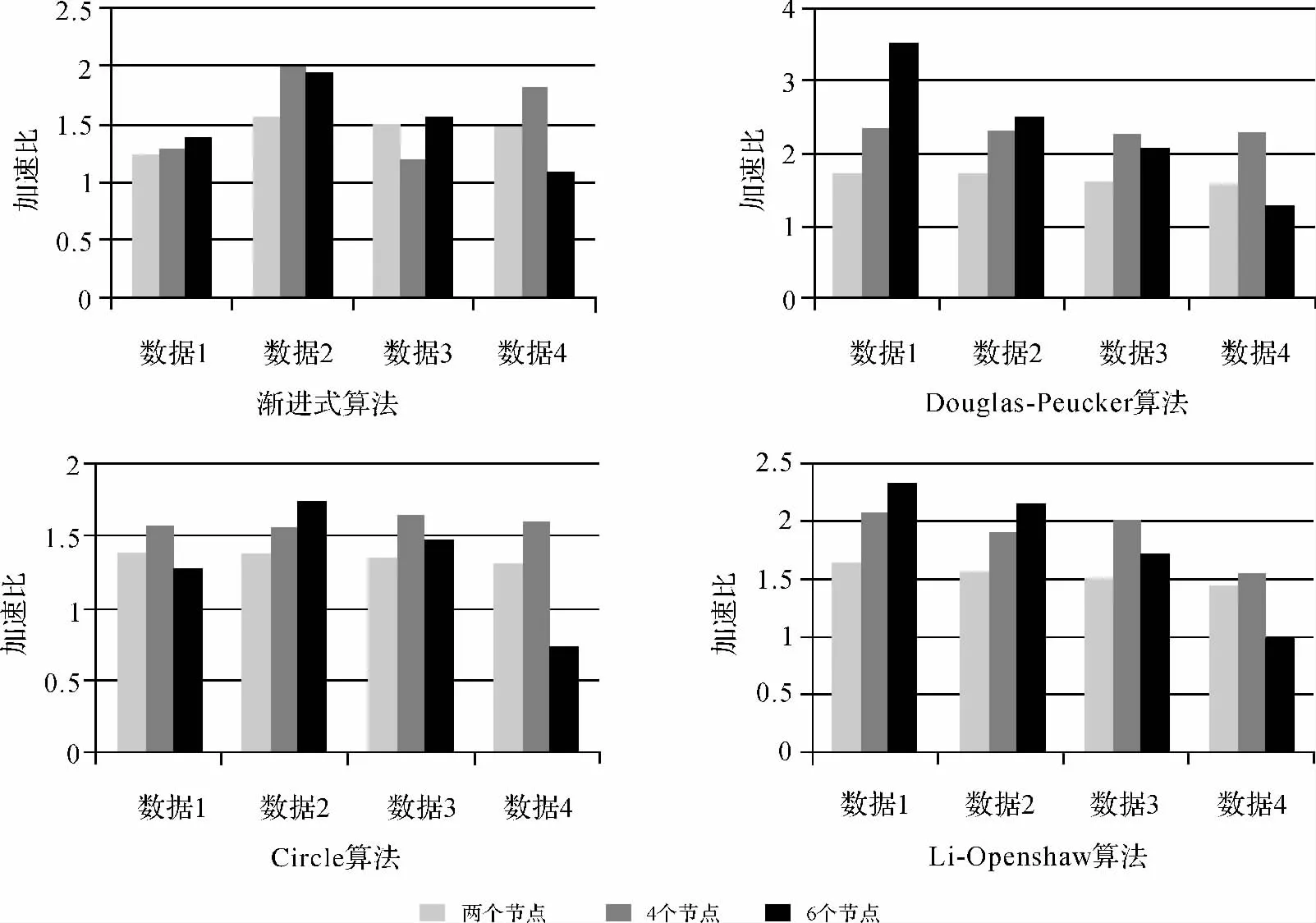
图8 非阻塞通信方式下简化算法加速比Fig.8 Speedup of the simplification algorithm under non－blocking communication

（2）算法约束参数与数据的空间分布特征共同影响算法的并行计算过程，导致渐进式算法加速比呈不规律变化。究其原因主要是数据分配方法虽然保证了计算节点上的负载均衡性，但是不同计算节点上的数据弯曲特征、转折点数量等对渐进式简化的约束参数产生了影响，导致不同计算节点上的计算任务不均衡，进而导致算法加速比的不均衡。

综上所述，简化算法并行效率受计算过程与通信过程两方面影响，在分析简化算法的并行计算适宜性时，应该综合考虑算法的时间复杂度、约束参数、数据量、数据分布特征以及计算环境等多个因素。

5 结 论

当前多核、集群等硬件资源不断发展，并行计算在地图综合乃至地学计算过程中正逐渐得到重视。本文基于MPI进行等高线简化算法的并行计算，探讨了MPI环境下等高线并行计算需要解决的关键问题。在对简化算法效率分析的基础上，选取4种典型的简化算法，利用数据量呈等差分布的等高线数据进行等高线简化并行试验。试验表明，算法并行计算效率并不总是随着节点数增加而提高，尤其是串行算法效率很高的算法；基于MPI的非阻塞通信方式相对于阻塞通信方式可以提高并行计算效率；不同的简化算法，其并行计算的最高加速比呈现于不同数量的计算节点上。

目前本研究提出的方法只是基于MPI的等高线简化并行计算，数据划分方法采用的是基于高程带的划分方法，还没有达到很好的负载均衡。而基于Linux的Pthread多线程模式、基于OpenMP与MPI的混合模式、MPI运行时参数优化、MPI进程摆放优化以及通信方式的优化对于地图综合并行计算的性能优化还有待于做进一步的深入研究。动态负载平衡、面向计算任务分解的并行计算、不同的并行计算环境等问题将是地图综合高性能计算所面临的新问题，将在今后的研究中得到更深入的探讨。

［1］ OOSTEROM V P，VRIES M D，MEIJERS M.Vario－scale Data Server in a Web Service Context［C］∥Proceedings of Workshop of the ICA Commission on Map Generalization and Multiple Representation.Vancouver：ICA，2006：1－14.

［2］ WANG Yanhui，LI Xiaojuan，GONG Huili.The Fundamental Issues of Multi－Scale Representation in the Geographic Elements［J］.Science in China，2006，36（z1）：38－44.（王艳慧，李小娟，宫辉力.地理要素多尺度表达的基本问题［J］.中国科学：E辑，2006，36（z1）：38－44.）

［3］ CECCONI A.Integration of Cartographic Generalization and Multi－scale Databases for Enhanced Web Mapping［D］.Zurich：Zurich University，2003.

［4］ GUO Qingsheng，HUANG Yuanlin，ZHENG Chunyan，et al.Spatial Reasoning and Incremental Map Generalization［M］.Wuhan：Wuhan University Press，2007：260－290.（郭庆胜，黄远林，郑春燕，等.空间推理与渐进式地图综合［M］.武汉：武汉大学出版社，2007：260－290.）

［5］ YANG B，PURVES R，WEIBEL R.Efficient Transmission of Vector Data over the Internet［J］.International Journal of Geographical Information Science，2007，21（1－2）：215－237.

［6］ ZHAO Yuan，ZHANG Xinchang，KANG Tingjun.A Parallel Ant Colony Optimization Algorithm for Site Location［J］.Acta Geodaetica et Cartographica Sinica，2010，39（3）：322－327.（赵元，张新长，康停军.并行蚁群算法及其在区位选址中的应用［J］.测绘学报，2010，39（3）：322－327.）

［7］ XIAO Han，ZHANG Zuxun.Parallel Image Matching Algorithm Based on GPGPU［J］.Acta Geodaetica et Cartographica Sinica，2010，39（1）：46－51.（肖汉，张祖勋.基于 GP GPU的并行影像匹配算法［J］.测绘学报，2010，39（1）：46－51.）

［8］ ZOU Xiancai，LI Jiancheng，WANG Haihong，et al.Application of Parallel Computing with OpenMP in Data Processing for Satellite Gravity［J］.Acta Geodaetica et Cartographica Sinica，2010，39（6）：636－641.（邹贤才，李建成，汪海洪，等.OpenMP并行计算在卫星重力数据处理中的应用［J］.测绘学报，2010，39（6）：636－641.）

［9］ QU Wanling，LIU Tian，WANG Hanpin，et al.Design and Analysis of Algorithms［M］.Beijing：Tsinghua University Press，2011：18－20.（屈婉玲，刘田，王捍贫，等.算法设计与分析［M］.北京：清华大学出版社，2011：18－20.）

［10］ ZHU Kunpeng.Quality Evaluation of Linear Features＇Simplification Algorithms［D］.Zhengzhou：Information Engineering University，2007.（朱鲲鹏.线要素化简质量评估［D］.郑州：信息工程大学，2007.）

［11］ CHEN Guoliang.Design and Analysis of Parallel Algorithms［M］.Beijing：Higher Education Press，2002.（陈国良.并行算法的设计与分析［M］.北京：高等教育出版社，2002.）

［12］ JIA Meili.Master－Slave Parallel Mind Evolutionary Computation Based on MPI［J］.Journal of North University of China（Natural Science Edition），2007，28（z1）：66－69.（贾美丽.基于MPI的主从式并行思维进化计算［J］.中北大学学报：自然科学版，2007，28（z1）：66－69.）

［13］ DAVY J R，DEW P M.A Note on Improving the Performance of Delaunay Triangulation ［M］.Tokyo：Springer Japan，1989：209－226.

［14］ QI Lin，SHEN Jie，GUO Lishuai，et al.Dynamic Strip Partitioning Method Oriented Parallel Computing for Construction of Delaunay Triangulation ［J］.Journal of Geo－Information Science，2012，14（1）：55－61.（齐琳，沈婕，郭立帅，等.面向D－TIN并行构建的动态条带数据划分方法与试验分析［J］.地球信息科学学报，2012，14（1）：55－61.）

［15］ LIU Zhiqiang，SONG Junqiang，LU Fengshun，et al.Optimizing Method for Improving the Performance of MPI Broadcast under Unbalanced Process Arrival Patterns［J］.Journal of Software，2011，22（10）：2509－2522.（刘志强，宋君强，卢凤顺，等.非平衡进程到达模式下MPI广播的 性 能 优 化 方 法 ［J］.软 件 学 报，2011，22（10）：2509－2522.）

［16］ DOU Zhihui.High Performance Computing for Parallel Programming Technology－MPI Parallel Program Design［M］.Beijing：Tsinghua University Press，2001.（都志辉.高性能计算之并行编程技术—MPI并行程序设计［M］.北京：清华大学出版社，2001.）

［17］ LIN Na.Research and Improvement of Submitting Job in MPICH ［D］.Shanghai：Fudan University，2006.（林娜.MPICH作业递交方式的研究及改进［D］.上海：复旦大学，2006.）

［18］ GUO Lishuai，SHEN Jie，ZHU Wei.Time Complexity Analysis of Line Simplification Algoritnms［J］.Journal of Geomatics Science and Technology，2012，29（3）：226－230.（郭立帅，沈婕，朱伟.线要素化简算法的时间复杂度分析［J］.测绘科学技术学报，2012，29（3）：226－230.）