基于面特征的遥感图像几何校正模型

龙腾飞，焦伟利，王 威

1.中国科学院 遥感与数字地球研究所，北京 100094；2.中国科学院大学 北京 100049

1 引 言

传统的遥感图像几何校正模型是基于控制点建立的，当能够准确获取地面控制点时，采用地面控制点进行几何校正能够较好地改善图像的定位精度；然而在很多困难地区的卫星影像上，如沙漠、山区等，很难辨认出准确的物理点特征，因此难以获得足够数量和足够准确的地面控制点，而线特征、面特征则更易获得（如已知的道路、水体等）。另一方面，在以不同分辨率影像作为参考数据源时，点的位置坐标也难以准确确定。事实上，就特征提取而言，提取有意义的面特征比提取有意义的点特征更容易，而且，无论自然环境还是人工环境中都存在丰富的面状地物，如建筑物、运动场、公园、湖泊等。参考影像、数字线划地图（DLG）、GIS矢量数据中存在大量的面特征，使用面特征进行几何校正能够充分地利用这些数据。

长期以来，人们主要关注基于点［1－3］、直线［4－6］和曲线［7］的图像配准与几何校正方法，近年来国内外的学者针对面状特征的提取［8－9］、面状特征的相 似性度 量［10－11］以 及 面 状 特 征 的 匹 配 策 略［12］等方面进行了一些研究，基于面状地物的图像配准方法已经应用于光学影像与SAR影像［13－14］、遥感影像与GIS数据的配准［15］，但是这些方法主要侧重于面状地物的提取和配准，很少涉及利用面特征来建立校正模型，进行图像几何校正。目前，已有的方法往往将面特征转化为点特征使用（如提取多边形的重心作为控制点［13，15］），最终基于点特征进行几何校正，并未充分利用面特征的信息。由于传感器的成像方式、侧视角、地形等的影响，影像上的面状地物会发生不同程度的变形，重心的位置也会发生改变，因此使用面状地物的重心作为控制点的方法存在缺陷。本文从面状特征的距离度量出发，直接利用面状特征的轮廓信息，提出一种基于面特征的图像几何校正方法。

2 基于面特征的几何校正模型

本文方法的关键技术是利用面特征建立和求解误差方程，其中误差方程的建立需要计算控制面多边形与像平面多边形之间的距离，多边形之间的距离以多边形上的点到多边形的距离为基础。因此，下面依次介绍点到多边形的距离计算方法、多边形到多边形的距离计算方法以及基于面特征的几何校正模型建立方法。

2.1 点到多边形的距离计算方法

首先给出点到多边形距离的定义：同一平面内，点p到多边形A的距离为多边形A所有边界点到点p的最小距离，特别的，当点p在多边形A内部时，距离为0。

记多边形的边界点集合为∂A，任意点p到多边形A的距离可表示为

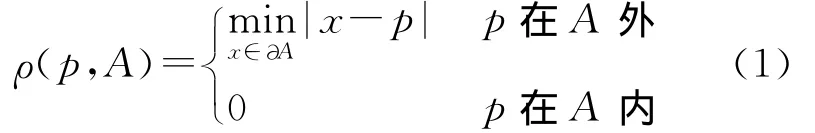
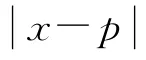
欲求点p到多边形A边界的最小距离，首先分别计算点p到多边形A各条边的距离，然后得到其最小值。其中，点p到多边形A某条边l的距离分为两种情况：过点p作线段l的垂线，若垂足在线段l上，则点p到垂足的距离为点p到l的距离；若垂足不在线段l上，则点p到线段l的两个端点的距离的较小值为点p到l的距离。图1为不同情况下点到线段的示意图。图1（a）中，垂足m在线段l上，则Vpm为点p到线段l的距离；图1（b）中，垂足m在线段l外，且Vpa＜Vpb，则Vpa为点p到线段l的距离。

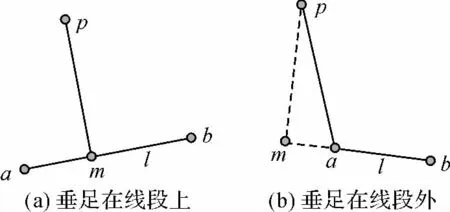
图1 不同情况下点到线段的距离Fig.1 Distance from point to line segment in different cases

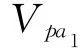
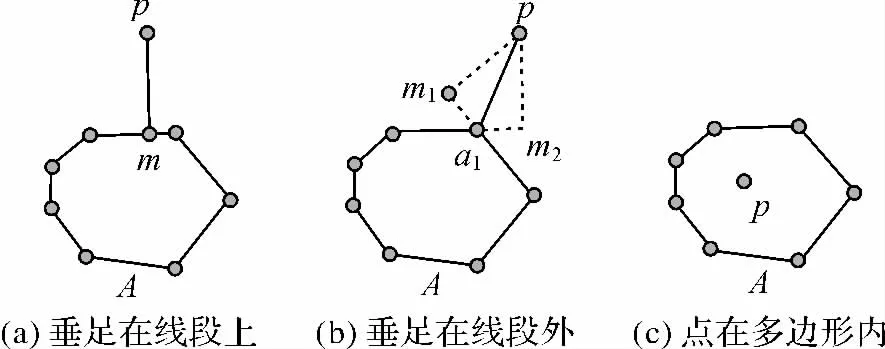
图2 不同情况下点到多边形的距离Fig.2 Distance from point to polygon in different cases

距离为标量，用于平差时缺乏方向性，故引入距离矢量的概念：若式（1）中，距离值在x＝a处取得，则定义点p到点a的矢量为点p到多边形A的距离矢量，记为ρ（p，A）。特别的，如果ρ（p，A）＝0，则ρ（p，A）＝0。

点p到多边形A的距离矢量算法如下。

步骤1：令ρ为一个很大的值max，令l为多边形A的第1条边。

步骤2：计算点p到线段l的距离矢量d及距离d。

步骤3：如果d＜ρ，则令ρ＝d，ρ＝d。

步骤4：如果l是多边形A的最后一条边，则转到步骤5；否则，令l为多边形A的下一条边，并转到步骤2。

步骤5：输出点p到多边形A的距离矢量ρ。

2.2 多边形到多边形的距离计算方法

在点到多边形距离的基础上给出多边形到多边形距离的定义：多边形A到多边形B的距离为多边形A所有边界点到多边形B的距离中最大者。

特别说明，多边形的边是由连续的边界点组成的，而多边形的顶点是多边形边的端点。图3说明了多边形的边界点和顶点的区别。

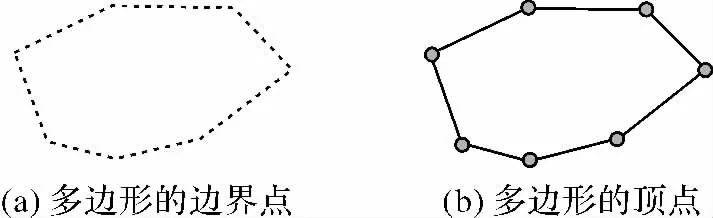
图3 多边形的边界点和顶点Fig.3 Boundary points and vertices of a polygon

多边形A到多边形B的距离可以表示为

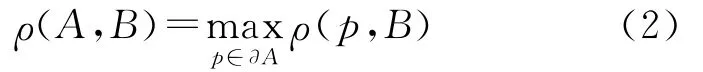
式中，p为多边形A的边界点。

利用该定义计算多边形之间的距离矢量时间复杂度较大，下面给出一个命题，可以简化多边形距离的计算。

命题1：多边形A到多边形B的距离为多边形A所有顶点到多边形B的距离中的最大值。

借助命题1，如果记多边形的顶点集合为~A，则多边形A到多边形B的距离可以表示为

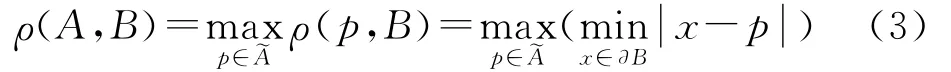
式中，p为多边形A的顶点；x为多边形B的边界点。

式（3）中，若多边形A到多边形B的距离值在p＝a，x＝b处取得，则定义点a到点b的矢量为多边形A到多边形B的距离矢量，记为ρ（A，B）。特别的，如果ρ（A，B）＝0，则ρ（A，B）＝0。

多边形A到多边形B的距离矢量算法如下。

步骤1：令ρ＝0，令p为多边形A的第一个顶点。

步骤2：计算点p到多边形B的距离矢量d及距离d。

步骤3：如果d＞ρ，则令ρ＝d，ρ＝d。

步骤4：如果p是多边形A的最后一个顶点，则转到步骤5，否则，令p为多边形A的下一个顶点，并转到步骤2。

步骤5：输出多边形A到多边形B的距离矢量ρ。

2.3 基于面特征的几何校正模型建立方法

经典的成像几何模型用来建立地面点三维空间坐标与相应像点二维平面坐标之间的关系，一般的，通用模型可表示为

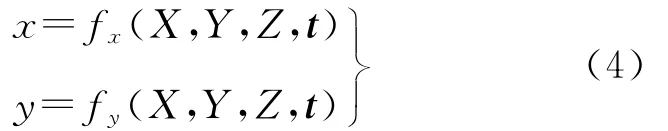
式中，t＝［t1，t2，…，tn］T表示传感器几何校正模型的n个参数；（X，Y，Z）表示控制点的地面坐标；（x，y）表示控制点在影像上的量测坐标。目前，常用的几何校正模型有严格成像模型、仿射变换模型、多项式模型、有理函数模型等，这些模型均可用式（4）来表示［6］，本文的方法可用于各种几何校正模型。下面说明利用控制面特征建立误差方程的过程。

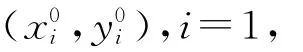
式（5）表示多边形A到多边形A0的距离矢量为0。由上节的定义可知，多边形A到多边形A0的距离必在多边形A的某一顶点处取得，不妨记为ak（xk，yk）∈~A，其中，k为整数，且1≤k≤m，则

式中，A0为常量，矢量ρ（ak，A0）具有水平方向和垂直方向的两个分量，可记ρ（ak，A0）＝（ρx，ρy），且根据式（4）有

式中，（Xk，Yk，Zk）为地面多边形A′的第k个顶点坐标，则式（6）等价于式（8）

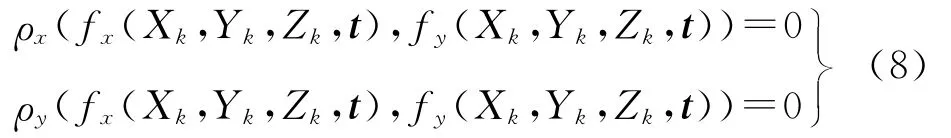
对式（8）进行线性化可以得到控制面特征的误差方程

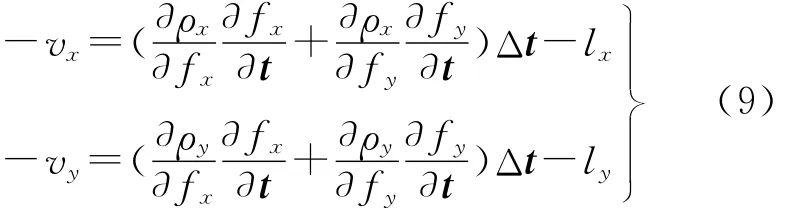
式中，vx和vy为随机误差；lx＝－ρx（fx，fy），ly＝－ρy（fx，fy）；Δt＝［Δt1，Δt2，…，Δtn］T表示t的改正向量。

这里ρx和ρy没有解析形式，可采用数值微分［16］的方法来逼近各函数偏导，如

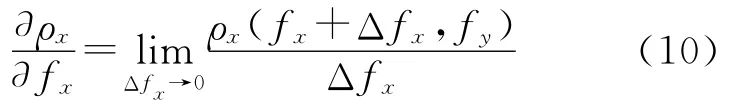
一个控制面特征可以导出如式（9）的两个误差方程，因此利用不少于n／2个控制面特征即可求解出模型中的n个未知参数t，参数的求解可使用 LM 算法［17－18］。

3 试验与分析

为验证上述方法的有效性，本文选用Landsat TM、ALOS PRISM和QuickBird 3种影像进行了试验。Landsat影像为安徽地区影像，摄于2008年4月，影像大小为6856像素×5733像素，分辨率为30m，影像范围内最大高程差为400m左右；ALOS影像为吉林地区影像，摄于2010年9月，影像大小为29 493像素×16 000像素，分辨率为2.5m，影像范围内最大高程差为400m左右；QuickBird影像为西宁地区的影像，摄于2010年10月，影像大小为24 523像素×33 549像素，分辨率为0.6m，影像范围内海拔均在2000m以上，最大高程差为1000m左右。

对每种影像分别进行4组试验。第1组试验中，均匀地选取若干个控制面特征，用本文方法进行几何校正；第2组试验中，在第1组试验所选的控制面特征上各选取一对对应的顶点作为控制点，用这些控制点进行几何校正；在1、2组试验的控制面和控制点中人为地加入两个粗差（5～15个像素），对每种影像的控制面和对应的控制点所加入的粗差相同；第3组试验用含有粗差的控制面进行几何校正；第4组试验用含有粗差的控制点进行几何校正。利用相同的检查点进行四组试验的精度评价。Landsat影像的试验采用其卫星轨道模型［19］，ALOS影像和QuickBird影像的试验采用基于像方补偿的有理函数模型［20］。面状特征的提取采用基于曲线演化的水平集方法［21］。

图4～图6分别显示了Landsat影像、ALOS影像和QuickBird影像试验中控制点、控制面和检查点的分布及示意图。各图中左边为控制点、控制面和检查点在整景影像中的分布图，其中青色三角形表示检查点，红色圆点表示控制点或控制面（图像缩小后控制面用点代替显示，与控制点重合）；右图为局部放大后的控制面和控制点示意图，控制面用红色轮廓表示，控制点用红色圆点表示。

图4 Landsat影像控制点、控制面及检查点示意图Fig.4 GCPs，GCAs and check points of Landsat image

图5 ALOS影像控制点、控制面及检查点示意图Fig.5 GCPs，GCAs and check points of ALOS image

图6 QuickBird影像控制点、控制面及检查点示意图Fig.6 GCPs，GCAs and check points of QuickBird image

表1列出了3种影像的4组试验结果，包括控制面的拟合精度、控制点的拟合精度以及检查点的精度。

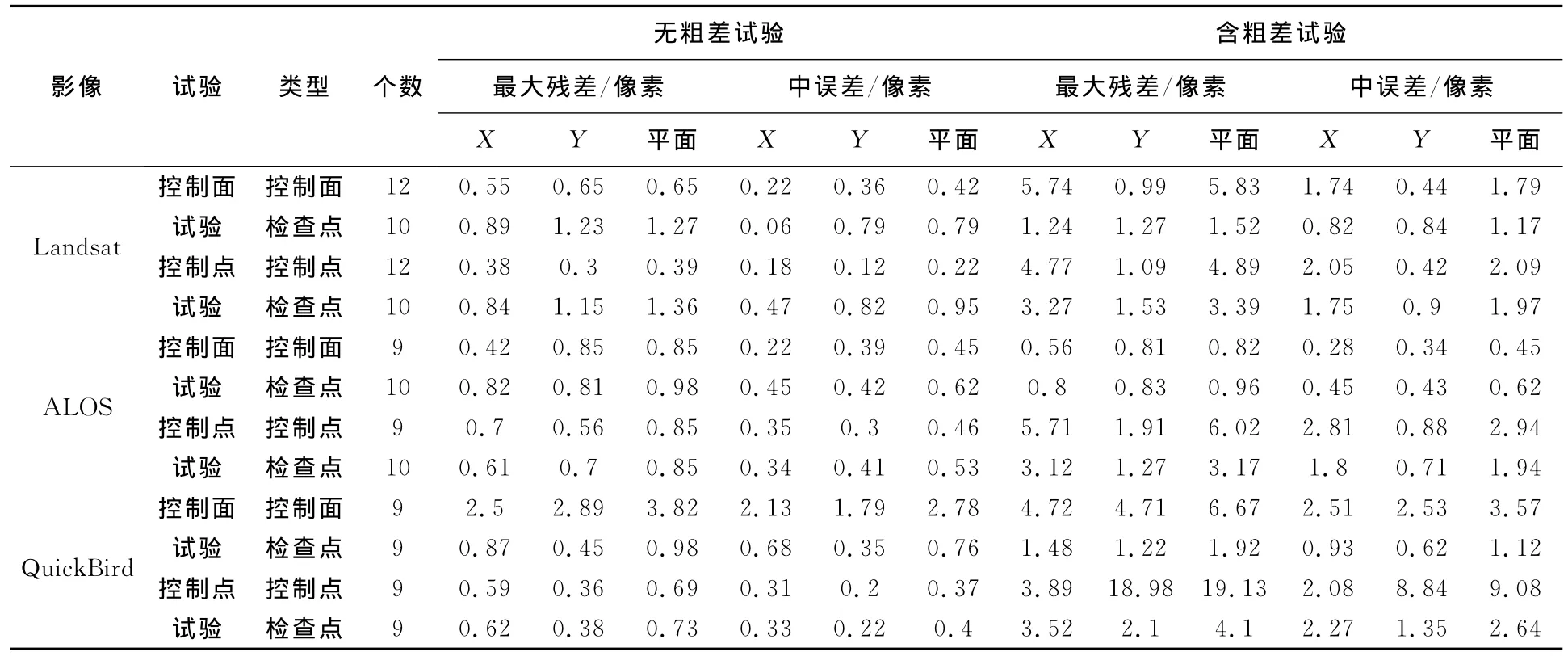
表1 试验结果对比Tab.1 Result comparison of tests

通过对表1结果的分析，可以得出以下结论。

（1）基于控制面的几何校正方法可以用于不同的卫星影像和不同的成像模型。

（2）当控制资料不含粗差时，使用控制面和控制点建立校正模型，图像校正精度基本一致。如表1所示，在Landsat、ALOS及QuickBird影像无粗差的试验中，使用控制面和使用控制点建立校正模型，进行几何校正，控制点和检查点的精度均能达到一个像素以内，两种方式的校正精度基本一致。

（3）试验中控制面的残差为根据几何模型计算出的多边形到参考多边形的距离，由多边形到多边形距离的定义可知，残差为计算多边形所有顶点到参考多边形距离的最大值，因此控制面的残差一般大于控制点的残差。

（4）当控制资料中含有粗差时，基于控制面的几何校正模型比基于控制点的几何校正模型具有更强的容错能力。如表1所示，在Landsat和QuickBird影像含有粗差的试验中，用控制点进行几何校正后，检查点的最大残差超过了3像素，而用控制面进行几何校正后，检查点的最大残差在2像素以内；在ALOS影像含有粗差的试验中，用控制点进行几何校正后，检查点的最大残差超过了3像素，而用控制面进行几何校正后，检查点的最大残差在1像素以内。其主要原因为：在Landsat和QuickBird的面特征校正试验中，加入粗差后，粗差点参与模型的解算会导致模型参数偏离真值，因此，该粗差对基于面特征的校正模型精度影响力受到限制；而在ALOS的面特征校正试验中，加入粗差后，粗差点落到了参考面多边形内部，其到参考面多边形的距离为0，对多边形距离的计算没有贡献，因此，该粗差对基于面特征的校正模型精度几乎没有影响。

（5）在QuickBird影像无粗差试验中，所选控制面特征的影像多边形和地面多边形的边界有一定的偏差，因此，控制多边形的拟合精度稍差，超过了2像素，但使用控制面进行几何校正的精度与使用控制点进行几何校正的精度相差不大，可以达到1像素左右。这也表明控制面具有较好的容错性。

（6）QuickBird影像范围海拔均在2000m以上，最大高程差为1000m左右，表1中QuickBird影像试验结果表明，基于控制面特征可用于高山地区影像的几何校正。

4 结 论

在实际应用中，足够数量和足够准确的地面控制点有时难以获得，而参考影像、数字线划地图、GIS矢量数据中存在大量的面特征，借助本文基于面特征的几何校正方法能够充分地利用这些数据。

（1）本文方法的本质仍然是点与点之间的计算，但其不要求地面多边形和影像多边形的顶点间具有一一对应的关系，因此对控制面的约束要求要比传统的控制点弱的多。尤其是对于圆弧状的地物，通常情况下无法找到对应的特征点，但将它作为一个整体的控制面，就可以用来进行图像的几何校正。

（2）本文方法不受具体成像模型的限制，可以根据影像自身的特点使用卫星轨道模型、有理函数模型、仿射变换模型等，具有通用性。

（3）由于面特征是由许多点组成的，个别点的误差对于控制面本身来说影响并不大，因此，基于面特征的几何校正方法比基于点特征的几何校正方法具有更强的容错能力。试验结果表明本文的方法可用于不同的卫星影像和成像模型，当控制资料不含粗差时，控制面和控制点的校正精度基本一致，可达到1像素以内；当控制资料中含有粗差时，用控制面校正的精度明显优于用控制点校正的精度。

本文方法是基于已有的控制面特征进行的，而控制面特征提取和匹配的自动化程度较低、耗时较多，提高控制资料准备过程的自动化程度是后续工作的一个方向。此外，由于成像时间、成像角度、数据源等条件的不同，面特征自动提取的方法对不同影像所提取的同名面特征往往并不具有完全一致的轮廓，这种不一致对几何校正结果的影响还需要进一步的研究和分析。

［1］ JI Shunping，YUAN Xiuxiao.Automatic Matching of High Resolution Satellite Images Based on RFM ［J］.Acta Geodatetica et Cartographica Sinica，2010，39 （6）：592－598.（季顺平，袁修孝.基于RFM的高分辨率卫星遥感影像自动匹配研究［J］.测绘学报，2010，39（6）：592－598.）

［2］ YANG Huachao，ZHANG Lei，YAO Guobiao，et al.An Automated Image Registration Method with High Accuracy Based on Local Homography Constraint［J］.Acta Geodatetica et Cartographica Sinica，2012，41（3）：401－408.（杨化超，张磊，姚国标，等.局部单应约束的高精度图像自动配准方法［J］.测绘学报，2012，41（3）：401－408.）

［3］ ZHANG Guo，CHEN Tan，PAN Hongbo，et al.Patch－based Least Squares Image Matching Based on Rational Polynomial Coefficients Model［J］.Acta Geodatetica et Cartographica Sinica，2011，40（5）：592－597.（张过，陈钽，潘红播，等.基于有理多项式模型的物方面元最小二乘匹配［J］.测绘学报，2011，40 （5）：592－597.）

［4］ LI Cailin，GUO Baoyun，LI Chang.The High－accurate Extraction of Line Features of Object Contour［J］.Acta Geodatetica et Cartographica Sinica，2011，40（1）：66－70.（李彩林，郭宝云，李畅.目标轮廓直线特征的高精度提取［J］.测绘学报，2011，40（1）：66－70.）

［5］ LONG Tengfei，JIAO Weili，WANG Wei.Geometric Rectification Using Feature Points Supplied by Straight－lines［J］.Procedia Environmental Sciences，2011，11：200－207.

［6］ LONG Tengfei，JIAO Weili，WANG Wei.Block Adjustment for Generic Geometric Model Using Points and Straight－Lines［J］.Advanced Materials Research，2011，268－270：584－589.

［7］ TANG Jinjun，CAO Kai.An Adaptive Trajectory Curves Map－matching Algorithm ［J］.Acta Geodaetica et Cartographica Sinica，2008，37（3）：308－315.（唐进君，曹凯.一种自适应轨迹曲线地图匹配算法［J］.测绘学报，2008，37（3）：308－315.）

［8］ ZHANG Ying，ZHANG Jingxiong.Edge Detection and Areal Feature Extraction Based on Improved LOG Operator［J］.Journal of Geomatics，2011，36（5）：8－10.（张盈，张景雄.基于LOG改进算子的边缘检测与面状特征提取［J］.测绘信息与工程，2011，36（5）：8－10.）

［9］ XIN Liang，ZHANG Jingxiong.Fast Extraction of Conjugated Area Features and Accurate Registration of Remote Sensing Image［J］.Geomatics and Information Science of Wuhan University，2011，36（6）：678－682.（辛亮，张景雄.共轭面状特征的快速提取与遥感影像精确配准［J］.武汉大学学报：信息科学版，2011，36（6）：678－682.）

［10］ WANG Xin.Research on Identical Entity Geometric Matching in Multi－source Spatial Data［D］.Zhengzhou：Information Engineering University，2008.（王馨.多源空间数据同名实体几何匹配方法研究［D］.郑州：信息工程大学，2008.）

［11］ HAO Yanling，TANG Wenjing，ZHAO Yuxin，et al.Areal Feature Matching Algorithm Based on Spatial Similarity［J］.Acta Geodaetica et Cartographica Sinica，2008，37（4）：501－506.（郝燕玲，唐文静，赵玉新，等.基于空间相似性的面实体匹配算法研究［J］.测绘学报，2008，37（4）：501－506.）

［12］ DONG Xiaohua，DENG Susu，SHI Wenzhong.A Probabilistic Theory－based Matching Method ［J］.Acta Geodaetica et Cartographica Sinica，2007，36（2）：210－217.（董小华，邓愫愫，史文中.基于概率的地图实体匹配方法［J］.测绘学报，2007，36（2）：210－217.）

［13］ DARE P，DOWMANR I.An Improved Model for Automatic Feature－based Registration of SAR and SPOT Images［J］.ISPRS Journal of Photogrammetry ＆ Remote Sensing，2001，56（1）：13－28.

［14］ ZHANG Dengrong，YU Le，CAI Zhigang.A Region Feature Based Automatic Matching for Optical and SAR Images［J］.Journal of China University of Mining ＆ Technology.2007，36（6）：843－847.（张登荣，俞乐，蔡志刚.基于面特征的光学与SAR影像自动匹配方法［J］.中国矿业大学学报，2007，36（6）：843－847.）

［15］ ZHANG Xiaodong，LI Deren，GONG Jianya，et al.A Matching Method of Remote Sensing Image and GIS Data Based on Area Feature［J］.Journal of Remote Sensing，2006，10（3）：373－380.（张晓东，李德仁，龚健雅，等.一种基于面特征的遥感影像与GIS数据配准方法［J］.遥感学报，2006，10（3）：373－380.）

［16］ BURDEN R L，FAIRES J D.Numerical Analysis［M］.Ninth Edition.Boston：Brooks／Cole，2011：174－179.

［17］ MORE J J.The Levenberg－Marquardt Algorithm：Imple－Mentation and Theory［J］.Numerical Analysis：Lecture Notes in Mathematics，1978，630：105－116.

［18］ LOURAKIS M I A.A Brief Description of the Levenberg－Marquardt Algorithm Implemented by Levmar［EB／OL］.2005－02－11［2012－01－02］.http：∥ www.ics.forth.gr／lourakis／levmar／.

［19］ CHEN Pengshan，JIAO Weili，JIA Xiupeng.Robust LM Algorithm and Its Application on Rigorous Physical Model［J］.Science Technology and Engineering，2009，9（16）：4614－4618.（陈朋山，焦伟利，贾秀鹏.抗差LM算法求解遥感影像严格物理模型［J］.科学技术与工程，2009，9（16）：4614－4618.）

［20］ GRODECKI J，DIAL G.Block Adjustment of Highresolution Satellite Images Described by Rational Polynomials［J］.Photogrammetric Engineering ＆ Remote Sensing，2003，69（1）：59－68.

［21］ SHI Y G，KARL W C.A Real－time Algorithm for the Approximation of Level－set Based Curve Evolution ［J］.IEEE Transaction on Image Processing，2008，17 （5）：645－656.