面状居民地匹配骨架线傅里叶变化方法

黄智深，钱海忠，郭 敏，3，刘海龙，王 骁

1.信息工程大学 地理空间信息学院，河南 郑州 450052；2.南疆测勤队，新疆 喀什 844200；3.61175部队，江苏 南京 210049

1 引 言

各级应用部门经常需要将多源空间数据进行集成与融合，增强其共享性，避免数据的重复采集，以节省人力物力。多源空间数据之间往往存在差异性［1］，空间数据匹配作为空间数据更新与融合的关键技术之一，越来越受到重视。

城市居民地是空间目标变化中最为活跃的要素之一，也是空间同名实体匹配中复杂性最强、最具挑战性的内容之一。目前，针对大比例尺城市面状居民地匹配的研究已有很多，例如基于面状居民地重叠面积的匹配［2］、基于面实体几何形状相似性的匹配［3－4，19］、基于知识的非空间属性数据通过计算属性项的相似度值而进行的匹配［5］、基于面质心进行粗匹配并结合多种匹配检验规则（如面积、面密度等）进行最终匹配［6］、基于模糊拓扑关系分类的匹配［7］、利用面实体重心距离与重叠面积的基于概率的匹配［8］、利用多级弦长函数以及中心距离函数对要素几何形状进行多级描述并建立相似性度量模型进行匹配等［18］。居民地多为不规则图形，形态复杂，主要依据其面积重叠率、大小、方向等进行匹配，不但算法复杂，且描述结果存在许多不确定性；同时，居民地作为大比例尺城市地图的主要组成部分，其数据量大，直接对其进行匹配操作，将导致整个匹配过程计算量大，匹配效率低等问题。

为解决大比例尺面状居民地匹配过程中数据量大、形态复杂、不确定性强等问题，首先对更新前面状居民地和更新后面状居民地分别提取能反映该居民地轮廓形态主要特征的骨架线；然后通过对双方骨架线进行傅里叶变换与分析，来实现多源居民地之间的匹配。该方法的特点在于：①把面状居民地转化为能够反映其轮廓主要形态特征的骨架线，一方面数据复杂性降低了，另一方面可以引入线要素的许多匹配算法，拓展了面要素匹配的技术途径；② 傅里叶变换的变换系数可较好地描述线状要素的形态特征，并将形态信息从空间域转化到频率域，特别对几何形态相似性判断具备较好的识别和区分能力，可很好地提高匹配的准确率。

同时，由于把面状居民地转化为骨架线进行匹配，研究对象作如下限定：① 匹配双方为相同或相近比例尺面状居民地；② 针对许多数据语义信息不完整的现实，主要研究几何匹配，暂不考虑语义信息；③ 由于面状居民地与其骨架线之间一一对应，因此本文只针对1∶1居民地匹配情形展开研究，而针对1∶n和m∶n（这实际上是跨比例尺之间匹配）等匹配情形暂不考虑，这是因为试验表明目前对多个居民地骨架线进行合并，其结果难以反映这些居民地的形态分布与轮廓特征，后续拟在本文研究基础上，通过空间拓扑关系约束展开进一步研究。

2 基于骨架线傅里叶变换的面状居民地匹配算法

本算法主要由以下4个步骤组成：

（1）面状居民地主骨架线提取。对匹配双方的居民地集分别提取骨架线，将2维居民地转化为1维骨架线，降低数据的复杂性，提高计算效率。

（2）骨架线插值计算。包括插值数据准备和插值计算实施。前者量化描述骨架线的几何形态特征；后者对前者的量化描述进行插值计算，为傅里叶变换打下基础。

（3）离散傅里叶变换。对插值计算后的骨架线几何形态数据进行离散傅里叶变换，将骨架线形态信息从空间域转到频率域，更加充分地反映骨架线的几何形态信息。

（4）计算匹配双方的相关系数，并据此进行匹配。根据傅里叶变换结果，计算更新前数据骨架线和更新后数据骨架线之间的相关系数，据此来确定面状居民地之间的匹配关系。下文将详细阐述。

2.1 居民地骨架线提取

目前提取骨架线的常见算法有：平行线切割中点连线法、内侧缓冲区法以及Delaunay三角网法［9－10］。平行线切割中点连线法简单、直观，但对复杂多边形（如含岛），往往得不到理想结果。内测缓冲区法原理为：对多边形内侧迭代做缓冲区，直至获取小于面积要求的内侧缓冲区，将该缓冲区形心连线作为骨架线［12］，该方法与第一种方法存在相似的问题。Delaunay三角网法具有很好的几何特性，能够方便建立起不同空间目标的空间邻近关系［11］，并能较为详细地反映面要素的几何形态特征。

综合考虑，本文选择Delaunay方法来提取面要素骨架线。图1是采用Delaunay方法提取面要素骨架线的原理图，图2是一个提取居民地主骨架线的例子。可以看出该方法能很好地反映居民地轮廓的主要形态特征，同时以主骨架线来代替居民地进行匹配，可有效降低居民地匹配的复杂度。

图1 采用Delaunay方法提取面要素骨架线原理图Fig.1 Pick up skeleton－line with Delaunay technique

图2 面状居民地轮廓及其主骨架线提取例子Fig.2 Example of a polygon habitation and its main skeleton line

2.2 骨架线插值计算

为描述骨架线的几何形态，把骨架线的每个直线段转换为长度和角度信息，即骨架线每个直线段都转化为一对坐标值（长度，角度），这种坐标点称为几何形态数据点。同时，原有骨架线几何形态数据点的数量往往不能满足匹配分析需求，需要对其进行插值计算。详细方法如下。

2.2.1 骨架线几何形态描述

骨架线几何形态描述主要包括骨架线起始点选择、骨架线长度特征描述、骨架线角度特征描述以及几何形态数据点生成4个部分。

2.2.1.1 骨架线起始点选取

进行骨架线长度指标和角度指标描述之前，需首先确定骨架线上的某一顶点为起始点P0，选择不同起始点P0，将会得到不同的几何形态描述数据。本文对起始点P0选取的依据为

即选择横坐标最小的节点为起始点，且设定角度特征描述中以顺时针方向为正。其优点在于：可以确保骨架线的长度特征和角度特征均为正，且分析结果可视化图形位于坐标系的第一象限内。

2.2.1.2 骨架线长度特征描述

对于骨架线长度特征，采用骨架线上各相邻节点之间的长度在骨架线全长中所占比率的形式进行描述。因为所有节点距之和与骨架线全长比值为1，所以该比率值又称为归一化距离［3］。其描述步骤为：① 从骨架线起始点开始，计算骨架线的全长及其任意两个相邻节点（设起点、终点也为节点）之间的长度；② 计算相邻节点距离在骨架线全长中所占比率，用长度比率值代替相邻节点间的实际长度值。具体实现公式骨架线全长

相邻节点距离所占比率

这里需注意两个方面：① 为方便后续数据的运算及可视化，需将长度比率数组的第一个数据赋0；②前面各段的长度比率值需在后面的比率数据中累加，最后一个线段的长度比率值应为1。

2.2.1.3 骨架线角度特征描述

对于骨架线角度特征，采用骨架线上各线段的实际坐标方位角进行描述。具体步骤为：① 从骨架线起始点出发，求得各线段的转角φk（以顺时针方向为正）；② 根据所求的转角φk，计算骨架线上各线段的坐标方位角θk（以顺时针方向为正）。转角φk计算公式

方位角计算公式：Δy＝yi＋1－yi，Δx＝xi＋1－xi

上述计算保证了θk均为正数。由于角度特征数据与骨架线上线段一一对应，即使在一条骨架线的角度特征描述过程中出现多次θk值相同的情况，但该值的计算存在先后关系，可以避免一对多情形的出现。另外，在角度特征数据存储时，从骨架线起始点出发，骨架线第一个线段的角度特征描述数据需进行两次记录，即将其同时存储在角度特征数组的第1位和第2位。这是因为，对于骨架线为直线这种特殊情况，其只有首端点和末端点，首端点和末端点之间只能计算一个方位角，该方位角与长度之间只能构成一个几何形态数据点，不能满足对直线骨架线的表达。因此需要将骨架线角度特征数组的第2个数据赋予与第1个数据相同的值。

2.2.1.4 骨架线几何形态数据点的生成

骨架线几何形态数据点由长度特征数据和角度特征数据共同组成。由于这两组数据数量相同，且生成时的起始点相同，因此可按照先后顺序，以长度特征为横轴，以角度特征为纵轴，一一对应，得到一系列有序的坐标对，这些坐标对即为骨架线的几何形态数据点。例如，图3中骨架线A的几何形态描述数据如表1所示。

表1 骨架线A几何形态描述数据结果表Tab.1 The data describing the geometry of skeleton line Ashowing

图3 骨架线A示意图Fig.3 The diagram of skeleton line A

2.2.2 几何形态数据点插值计算

如果几何形态数据点数量过少，则不能满足相似性分析需求，这就需要对其插值，进一步突出骨架线主要几何形态特征，特别是整体形态特征。为避免出现新的误差，对待匹配双方骨架线必须采用相同插值方法进行插值。常用插值方法有拉格朗日插值、厄尔米特插值法以及样条插值法等［13］。

拉格朗日插值法是高次多项式插值，插值结果光滑，但不能保证插值收敛性，容易引起新的误差或不确定性；厄尔米特插值法属于低次多项式插值，使用简单，但是插值后曲线过于粗糙；三次样条插值法也属于低次多项式插值，但较厄尔米特插值法有较大改进，可有效确保插值后骨架线的准确性［14］。本文采用三次样条插值法，方法如下［15］。

由于长度特征数据采用归一化距离，其值域为x∈［0，1］，插值时首先将［0，1］区间进行等分，然后以区间等分点处的坐标值为插值点，以骨架线几何形态数据点为样条节点，进行插值运算。

在每个［xi－1，xi］区间上，三次样条函数可以表示为以下形式

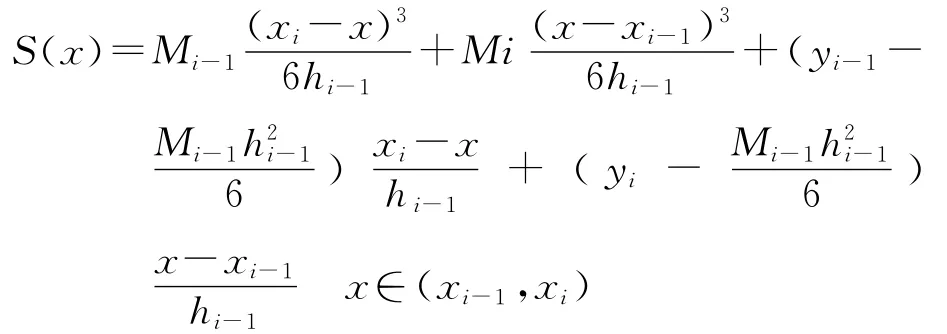
式中，hi－1＝xi－xi－1；Mi＝Sn（xi）。

Mi所满足的方程

式中

边界条件有如下两种：

第一型插值条件

由此导出

自然样条

由此得出M1＝0、Mn＝0，从而得出Mi满足三对角方程。

以图4中所示的待匹配骨架线为例，其几何形态特征数据点的正切空间图形如图5所示，对图5中的两条待匹配骨架线的几何形态特征图形进行三次样条插值分析，将（0，1）区间等分成50份，如图6所示。对比图5和图6可知，三次样条插值后，骨架线几何形态数据由直方图转化为曲线，不但丰富了几何形态数据点，而且骨架线几何特征的整体趋势以及局部差别也更为直观。

图4 某更新前及更新后居民地骨架线ig.4 The skeleton lines’before and after updating

图5 骨架线几何形态数据的可视化结果Fig.5 Visualization of skeleton lines geometry data

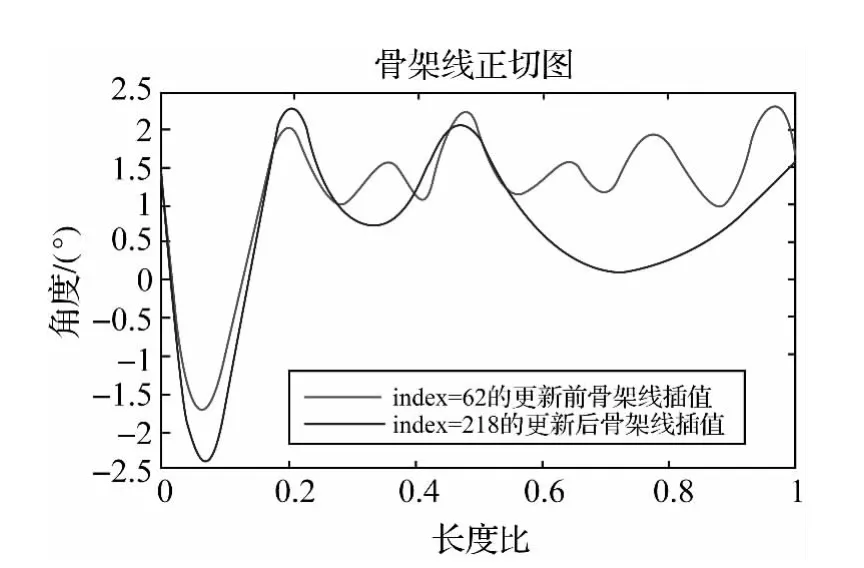
图6 对图5进行三次样条插值后的结果Fig.6 The result of cubic spline interpolation to fig.5

2.3 离散傅里叶变换

对经过三次样条插值的骨架线几何形态数据进行离散傅里叶变换，其主要变换过程［15］如下。

令ωn＝e－i2π／n，对于N个离散数据点xk（k＝0，1，…，N－1），进行如下变换

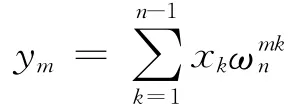
经过离散傅里叶变换，将各个离散数据点xk分解为它的基本频率的组合，也就是变换之后y的各个分量。为提高算法效率，采取离散傅里叶变换中的快速傅里叶变换，其变换过程如下

骨架线几何形态数据经过离散傅里叶变换，其结果由实数和虚数两部分组成。图6的插值结果经离散傅里叶变换，其实数和虚数部分如图7所示。

图7 骨架线离散傅里叶变换后数据图像Fig.7 The graphies of the skeleton line discreted with Fourier transform

2.4 相关系数计算

傅里叶变换后的骨架线几何形态特征数据，只是将骨架线信息从空间域转到频率域，还不能反映骨架线之间的差异。为量化描述骨架线之间在频率域的相似性，进一步采用相关系数进行描述。因为几何形态特征数据为离散数据，因此采用离散相关系数进行表达。离散相关系数的一般定义如下。

设｛gk｝和｛hk｝为两个未经傅里叶变换的离散数组，k＝1，2，…，n，则｛gk｝与｛hk｝的离散相关系数Cgh的一般计算公式如下［17］

在离散傅里叶变换的基础上求取相关系数，根据相关离散定理［15］，如果｛gk｝和｛hk｝经过离散傅里叶变换后分别为｛Gk｝、｛Hk｝，则Cgh等于｛Gk｝·｛Hk｝＊的逆离散傅里叶变换，其中星号表示复共轭。其中，逆离散傅里叶变换的一般过程如下

根据上述分析结果，设未经傅里叶变换之前的待匹配双方骨架线的几何形态描述数据分别为｛gk｝和｛hk｝，对其进行离散傅里叶变换的结果分别为｛Gk｝、｛Hk｝。令DFT和DFT－1分别代表离散傅里叶变换和逆离散傅里叶变换，则

令Z＝｛G｝·｛H｝＊，其中｛H｝＊为表示｛H｝的复共轭。对Z进行逆傅里叶变换，其结果即为离散相关系数，相关公式如下

相关系数的值域为［－1，1］区间，当Cgh＞0时，表示两要素同向相关，否则表示异向相关，Cgh的绝对值越接近1，表示两数组的相似性越高；越接近0，表示两数组的相似性越低。由于在进行骨架线几何形态描述时统一了骨架线描述的起始点，从而保证了待匹配双方骨架线几何形态描述数据的同向性，所以离散相关系数的取值区间为［0，1］。

3 试验验证及分析

3.1 试验验证

以某城市同一区域1∶1万的更新前面状居民地和更新后面状居民地作为试验数据，进行算法验证。详细匹配流程如图8所示。

图8 基于骨架线傅里叶变换的居民地匹配流程图Fig.8 The flowchart of habitation matching based on their skeleton lines by the Fourier transform

（1）面状居民地骨架线提取：提取居民地骨架线［16］，图9为更新前居民地及其骨架线，图10为更新后居民地及其骨架线。

（2）插值计算：分别对图9和图10中的骨架线进行几何形态描述，把几何坐标转化为“长度－角度”坐标系下的几何形态数据，然后对其采用三次样条插值法进行插值计算。

图9 更新前居民地及对其提取骨架线的结果Fig.9 Block data before the update，and the result of getting their sketch lines

图10 更新后居民地及对其提取骨架线的结果Fig.10 Updated block data，and the result of getting their sketch lines

（3）傅里叶变换及相关系数计算：根据插值结果，分别对更新前居民地骨架线和更新后居民地骨架线的几何形态数据进行离散傅里叶变换，并计算相关系数。将相关系数与指定阈值比较，若相关系数大于指定阈值，则认为双方骨架线之间几何形态吻合，满足匹配条件，进而认定骨架线所对应的居民地之间匹配成功；反之，匹配失败。

这里，相关系数阈值的设定对匹配结果有直接影响。相关系数取值区间为［0，1］，相关系数越接近1，表明待匹配双方骨架线的几何形态差异越小；反之越接近0，说明待匹配双方骨架线的几何形态差异越大。相关系数阈值是待匹配双方骨架线基于傅里叶变换的几何形态相似程度标准。例如设置阈值为0.9时，本算法的各类匹配信息如表2所示（该阈值大小的设置可根据实际情况有所不同）。

相关系数阈值为0.9时，匹配结果如下：共有81块更新前居民地参与匹配，成功匹配71块，无法匹配10块（其中已拆除居民地8块）。共有77块更新后居民地参与匹配，成功匹配71块，无法匹配6块（其中新增居民地4块）。更新前居民地匹配总成功率为：87.7%（71／81），实际参与匹配成功率为：97.3%（71／（81－8））；更新后居民地匹配总成功率为：92.2%（71／77），实际参与匹配成功率为：97.26%（71／（77－4））。试验表明本方法具有较高的匹配正确率。

表2 更新前居民地和更新后居民地匹配的各类信息计算结果（局部）Tab.2 Statistic matching information of block data before update and updated habitation（part）

3.2 试验对比分析

面要素匹配方法大致可分为两类［21］，一类是简单形状描述法，如包围盒法、弦长面积描述法、面积周长比法等；另一类是详细轮廓描述法，如矩描述子、小波变换法等。前一类方法借助面要素轮廓的某些特征进行概略描述，没有区分出主要形态信息和次要形态信息；后一类方法可非常详细地反映居民地轮廓信息，但对细节信息过于敏感，不但匹配时计算量较大、匹配过程复杂，而且存在不确定性。相对已有算法而言，本方法的优势在于：重点对居民地的主要形态信息进行分析，有效降低了匹配过程中的不确定性，提高了匹配准确率。

为进一步验证本方法科学性，采用同一数据、不同方法的匹配结果进行比较（仍以图9、10为例）。图11是本方法匹配结果，图12是骨架线缓冲区法匹配结果；图13是矩描述子法匹配结果，图14是弦长面积法匹配结果。图11至图14中，高亮色显示的居民地为未匹配成功的居民地。图11和图12中居民地内的折线为提取的骨架线。

图11 采用本方法进行居民地匹配结果Fig.11 Matching result of habitations using the method termed in this paper

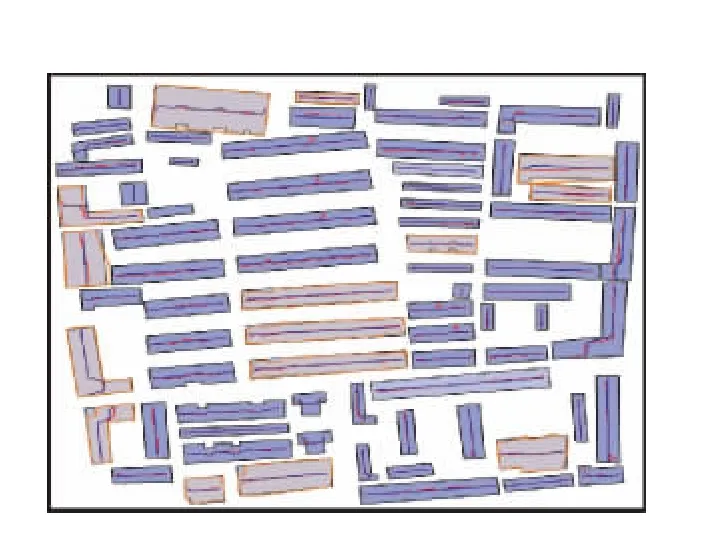
图12 采用骨架线缓冲区法进行居民地匹配结果Fig.12 Matching result of habitations by the method of skeleton lines′buffers

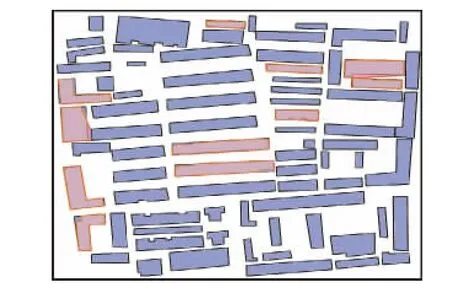
图13 采用矩描述子法进行居民地匹配结果Fig.13 Matching result of habitations with moment describe method

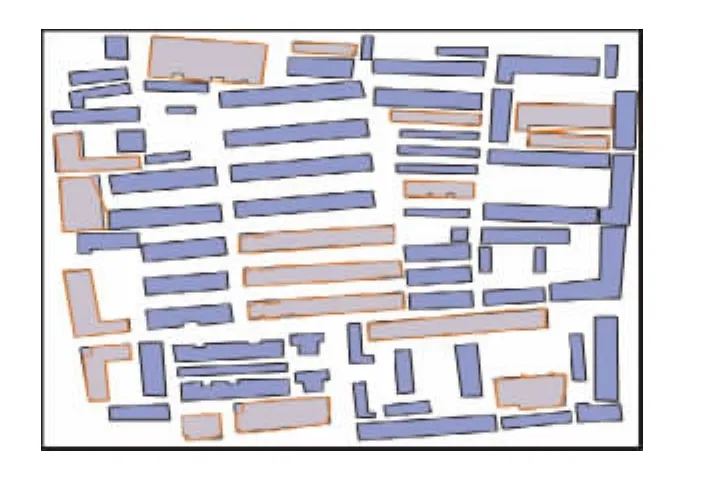
图14 采用弦长面积法进行居民地匹配结果Fig.14 Matching result of habitations by chord length and area method

不同匹配结果对比如表3所示。从表3可知，本方法匹配成功率优于另外3种匹配算法，进一步证明了本方法的科学性和优越性。同时，图12采用的方法为骨架线缓冲区匹配方法，该方法实际上是本文方法的前期研究成果，即对面状居民主骨架线进行缓冲区分析，并依据骨架线缓冲区之间的面积叠置率来判断是否匹配成功；其缺陷在于把骨架线还原为缓冲区后，骨架线的形态特征被弱化，不确定性增强了，影响了匹配正确率。而本方法对居民地主骨架线采用傅里叶变换的变换系数来表达，并将形态信息从空间域转化到频率域，特别对几何形态相似性判断具备较好的识别和区分能力，从而有效提高了匹配准确率。

4 结 论

本文提出了一种大比例尺城市面状居民地匹配方法，对同一区域大比例尺异源居民地进行等级化处理，得到能够反映面状居民地主要形态特征的骨架线，然后对骨架线进行几何形态描述、插值计算、傅里叶变换以及相关系数计算等操作，并依据相关系数的大小对骨架线进行匹配判断，最终根据骨架线的匹配完成面状居民地的匹配。该方法有效降低匹配数据的复杂性和可能产生的不确定性因素，提高几何形态相似性的识别与区分能力，同时匹配速度、正确率也得到提高。

表3 采用不同方法居民地匹配情况对比表Tab.3 Comparing results of matching habitations with different matching methods

［1］ GUO Li.Theory and Method Research on Multi－sources Geospatial Vector Data Fusion［D］.Zhengzhou：Information Engineering University，2008：51－52.（郭黎.多源地理空间矢量数据融合理论与方法研究［D］.郑州：信息工程大学，2008：51－52.）

［2］ GUO Li，ZHENG Haiying，WANG Hao.Study for Area Feature Matching Technique Based on Area Similarity［J］.Hydrographic Surveying and Charting，2009，29（3）：12－15.（郭黎，郑海鹰，王豪.面状矢量空间数据匹配技术研究［J］.海洋测绘，2009，29（3）：12－15.）

［3］ FU Zhongliang，SHAO Shiwei，TONG Chunya.Multi－scale Area Entity Shape Matching Based on Tangent Space［J］.Computer Engineering，2010，36（17）：216－220.（付仲良，邵世维，童春芽.基于正切空间的多尺度面实体形状匹配［J］.计算机工程，2010，36（17）：216－220.）

［4］ HAO Yanling，TANG Wenjing，ZHAO Yuxin，et al.Areal Feature Matching Algorithm Based on Spatial Similarity［J］.Acta Geodaetica et Cartographica Sinica，2008，27（3）：501－506.（郝燕玲，唐文静，赵玉新，等.基于空间相似性的面实 体 匹 配 算 法 研 究 ［J］.测 绘 学 报，2008，27（3）：501－506.）

［5］ COBB M，CHUNG M，FOLEY H.A Rule－based Approach for the Conflation of Attributed Vector Data ［J］.Geo Informatica，1998，2（1）：7－35.

［6］ YUAN S，TAO C.Development of Conflation Components［C］∥Proceedings of Geo－informatics‘99Conference.Ann Arbor：［s.n.］，1999：1－13.

［7］ ZHANG Qiaoping，LI Deren，GONG Jianya.A Real Feature Matching among Urban Geographic Databases［J］.Journal of Remote Sensing，2004，8（2）：107－112.（张桥平，李德仁，龚健雅.城市地图数据库面实体匹配技术［J］.遥感学报，2004，8（2）：107－112.）

［8］ TONG Xiaohua，DENG Susu，SHI Wenzhong.A Probabilistic Theory－based Matching Method ［J］.Acta Geodaetica et Cartographica Sinica.2007，36（2）：210－217.（童小华，邓愫愫，史文中.基于概率的地图实体匹配方法［J］.测绘学报，2007，36（2）：210－217.）

［9］ CAI Mengyi，TIAN Desen.Newly Organized Cartography Tutorial［M］.Beijing：Higher Education Press，2000：109－110.（蔡孟裔，田德森.新编地图学教程［M］.北京：高等教育出版社，2000：109－110.）

［10］ HUANG Zhishen，QIAN Haizhong.Dimension Decreaseoriented Habitation Matching Method ［J］.Journal of Geomatics Science and Technology，2012，29（1）：75－78.（黄智深，钱海忠.基于降维技术的面状居民地匹配方法［J］.测绘科学技术学报，2012，29（1）：75－78.）

［11］ QIAN Haizhong，WU Fang，ZHU Kunpeng，et al.A Generalization Method of Street Block Based on Dimensionreducing Technique［J］.Acta Geodaetica et Cartographica Sinica，2007，36（1）：102－108.（钱海忠，武芳，朱鲲鹏，等.一种基于降维技术的街区综合方法［J］.测绘学报，2007，36（1）：102－108.）

［12］ LIU Xiufang，YANG Yongping，LUO Ji，et al.Research on Extracting Polygon Skeleton by Using Inner Buffering Algorithm ［J］.Hydrographic Surveying and Charting，2010，30（5）：46－48.（刘秀芳，杨永平，罗吉，等.基于内侧缓冲区算法的多边形骨架线提取模型［J］.海洋测绘，2010，30（5）：46－48.）

［13］ CHEN Jie.A Valuable Book of MATLAB［M］.Beijing：Publishing House of Electronics Industry，2010：139－170.（陈杰.MATLAB宝典（第二版）［M］.北京：电子工业出版社，2010：139－170.）

［14］ LIU Zhenjun.A Valuable Book of Matlab in Scientific Calculation and Visualization［M］.Beijing：Publishing House of Electronics Industry，2009：191－210.（刘正君.Matlab科学计算与可视化仿真宝典［M］.北京：电子工业出版社，2009：191－210.）

［15］ HE Guangyu.Frequently－used Numerical Arithmetic Aggregation of Visual C＋＋［M］.Beijing：Science Press，2002：99－100.（何光愈.Visual C＋＋常用数值算法集［M］.北京：科学出版社，2002：99－100.）

［16］ WANG Xin.Research on Identical Entity Geometric Matching in Multi－Source Spatial Data［D］.Zhengzhou：Information Engineering University，2008：10－11.（王馨.多源空间数据同名实体几何匹配方法研究［D］.郑州：信息工程大学，2008：10－11.）

［17］ XU Jianhua.Mathematical Methods in Contemporary Geography［M］.Beijing：Higher Education Press，2002：37－38.（徐建华.现代地理学中的数学方法［M］.北京：高等教育出版社，2002：37－38.）

［18］ AN Xiaoya，SUN Qun，XIAO Qiang，et al.A Shape Multilevel Description Method and Application in Measuring Geometry Similarity of Multi－scale Spatial Data［J］.Acta Geodaetica et Cartographica Sinica，2011，40（4）：495－501.（安晓亚，孙群，肖强，等.一种形状多级描述方法及在多尺度空间数据几何相似性度量中的应用［J］.测绘学报，2011，40（4）：495－501.）

［19］ TANG Luliang，LI Qingquan，YANG Bisheng.Shape Similarity Measuring for Multi－resolution Transmission of Spatial Datasets over the Internet［J］.Acta Geodaetica et Cartographica Sinica，2009，38（4）：336－340.（唐炉亮，李清泉，杨必胜.空间数据网络多分辨率传输的几何图形相似性度量［J］.测绘学报，2009，38（4）：336－340.）

［20］ XU Junkui，WU Fang，WEI Huifeng.Research on Spatial Cognition Character of Areal Settlement Matching Process［J］.Journal of Geomatics Science and Technology，2012，29（4）：303－307.（许俊奎，武芳，魏慧峰.面状居民地匹配的空间认知特点研究［J］，测绘科学技术学报，2012，29（4）：303－307.）

［21］ ZHAI Renjian.Research on Automated Matching Methods for Multi－Scale Vector Spatial Data Based on Global Consistency Evaluation［D］.Zhengzhou：Information Engineering University，2011：82－87.（翟仁健.基于全局一致性评价的多尺度矢量空间数据匹配方法研究［D］.郑州：信息工程大学，2011：82－87.）