基于带宽自适应滤波的低频振荡Prony分析

杨芳，马建伟，杨利波

（1.广东电网清远供电局，广东 清远 511500；2.贵阳供电局，贵州 贵阳 550000；3.湖南省电网工程公司，湖南 衡阳； 421002）

1 引言

随着电力系统的日益发展和复杂化，大规模电网的互联，电力系统低频振荡问题日益突出，已经危及到电力系统的安全稳定运行［1，2］。

目前基于量测轨迹的低频振荡模式识别的方法主要有傅里叶算法［3］、小波算法［4］、Prony 算法［5－7］等。傅里叶算法精度受数据窗的限制，无法反映信号衰减信息从而不能正确反映信号的特征。小波算法可以反映信号的时变特性，在时域和频域分析中都有很好的分辨能力，但存在小波基难以选取的问题。Prony方法是通过一组指数函数的线性组合来拟合等间隔采样数据，从而估算出给定信号的频率、衰减、幅值、相位等信息，算法简便，因此被广泛用于电力系统低频振荡模式的识别。但是Prony算法对信号输入要求很高，对噪声较为敏感，识别含噪低频振荡信号时误差较大，因此在采用Prony法分析含噪声信号前需要进行滤波预处理［8－10］。文献［8］采用低通滤波器进行信号预处理，但在使用低通滤波器时，需进行时频变换之外，还需预先设定相应滤波器的截止频率和信号带宽，这对仅从实际信号确定滤波器参数和所需系统模型相对困难。文献［9］采用模糊滤波预处理，但模糊系统缺乏自学习和自适应能力，其隶属函数参数的调整、模糊推理规则的制定依赖于启发式知识和人类专家的经验，而这类知识有时很难获得；文献［10］提出采用基于小波对信号预处理，但此方法存在小波基难以选择，分层数和阀值难以确定等问题。文献［11］研究了基于递推最小二乘法（RLS）的自适应滤波及其在DSP上的实现，不需预先知道信号及其噪声的自相关范数，可以自动调节滤波器参数，实现最佳滤波，效果较好。

鉴于此，本文采用基于RLS的神经网络自适应滤波方法对带噪信号进行预处理，提高了算法的可靠性和适应性，再进行Prony分析。另外，可通过调节性能指标阀值，实现计算速度和精度的平衡。

2 带宽理论

信号带宽是指信号频谱的宽度，它由信号（或噪声）的能量谱密度或功率谱密度在频域中的分布规律确定的，单位Hz。

设低频振荡信号为

则截断时间内e－at的傅里叶变换为

低频振荡的傅里叶变换为:

由帕萨瓦定理可知低频振荡信号在正频域内的总能量为

3 基于带宽分析的余弦基神经网络的滤波研究

对于非周期低频振荡信号f（t），（0≤t≤T）将f（t）以周期T延拓而成的周期信号记为fp（t），则有

其中m为整数，显然，当时间t为0≤t≤T时有:fp（t）=f（t），因而周期信号fp（t）的连续时间傅里叶级数在周期（0≤t≤T）内同样可表示为式（5）的形式。

对于频带有限信号f（t）（0≤w≤Nw0），式（5）可改写为

只要获得an和bn，就得到了信号x（t）的幅度谱特性An和相位特性φn。当x（t）是复杂信号或未知信号时，求an和bn是困难的，将上式离散化为下列形式:

式中Ts为采样周期，且Ts≤π/ωmax，采样序列k=0，1，…，M，其中M=T/Ts。

由式（7）可建立余弦基神经网络［14］，如图1所示。

图1 神经网络模型

图中，wi为神经网络权值，ci为为隐层神经元激励函数，即

设权值矩阵W=［w0，w1，…，wN－1］T，激励矩阵C=［c0，c1，…，cN－1］T

则神经网络的输出为

其误差函数为

设误差矩阵为:

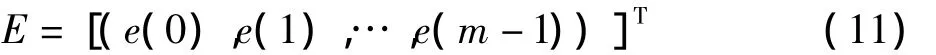
则性能指标为

权值调整量（梯度下降法）:

权值调整:

其中η为学习率，且0≤η≤1，α为动量因子，且0≤α≤1。

经过多次迭代运算，当性能指标达到所要求的精度范围后，对此时的权值进行分析，确定带宽范围，取带宽内的信号部分，可得滤波后低频振荡信号。

为了比较滤波前后的有效性，定义公式如下:信噪比:

误差:

其中:f（n）为输入的理想信号；^f（n）加噪后信号或滤波后信号。

图2 理想信号波形

4 仿真分析

4.1 叠加脉冲噪声信号的滤波识别分析

算例1，设低频振荡主导模式为

对该信号加入脉冲噪声干扰，如图3所示。我们取采样周期为Ts=0.01s，时间长度为T=10s，频率阀值~ω=2.5Hz，图2为理想信号波形，图3为加脉冲噪声的波形，图4为固定带宽滤波后波形与加噪前理想信号的比较，图5为动态带宽滤波后波形与加噪前理想信号的比较。表1为滤波前后效果对比分析，表2为滤波后的模式辨识结果。

图3 加脉冲噪声的波形

图4 固定带宽滤波后波形与加噪前信号的比较

图5 动态带宽滤波后波形与加噪前信号的比较

表1 滤波前后效果对比分析

表2 滤波后的模式辨识结果

由图3可知，在信号2s，5.5s，7.5s处加入了脉冲噪声，如果直接进行Prony分析则会出现大量多余模式，且误差较大。由图4和图5可知，其中蓝线为滤波后信号，红线为加噪前信号，它们几乎重合在一起，滤波效果较好，由表1、2可知，余弦神经网络方法有效的滤除了脉冲噪声，提高了信号的信噪比，提高了Prony法的抗噪性。其中固定带宽滤波效果要略好于动态带宽滤波法。

4.2 叠加高频噪声信号的滤波识别分析

算例2，对算例1中的信号加入工频的3次谐波和5次谐波的高频噪声干扰，即

对该信号加入高频谐波噪声的干扰，如下图所示。我们取采样周期为Ts=0.01s，时间长度为T=10s，频率阀值~ω=2.5Hz。图6为加噪后波形，图7为固定带宽滤波后波形与加噪前信号的比较，图8为动态带宽滤波后波形与加噪前信号的比较。表3为滤波前后效果指标分析，表4为滤波后的辨识结果。

图6 加高频谐波噪声的波形

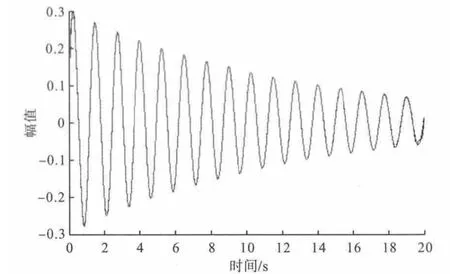
图7 固定带宽滤波后波形与加噪前信号的比较

图8 动态带宽滤波后波形与加噪前信号的比较

表3 滤波前后效果指标分析

表4 滤波后的辨识结果

由图7和图8可知，其中蓝线为滤波后信号，红线为加噪前信号，两者几乎重合在一起，滤波效果较好。由表3、4可知，余弦神经网络方法有效的滤除了高频谐波噪声，提高了信号的信噪比，提高了Prony法的抗噪性。其中固定带宽滤波效果要略好于动态带宽滤波法。

4.3 叠加白噪声信号的滤波识别分析

算例3，对算例 1中的信号加入信噪比为24.8112dB的白噪声干扰，如图9所示。我们取采样周期为Ts=0.01s，时间长度为T=20s，频率阀值~ω=2.5Hz，图9为加噪后波形，图10为固定带宽滤波后波形与加噪前信号的比较，图11为动态带宽滤波后波形与加噪前信号的比较。表5为滤波前后效果指标分析，表6为滤波后Prony分析结果。

图9 加白噪声后的波形

图10 固定带宽滤波后波形与加噪前信号的比较

图11 动态带宽滤波后波形与加噪前信号的比较

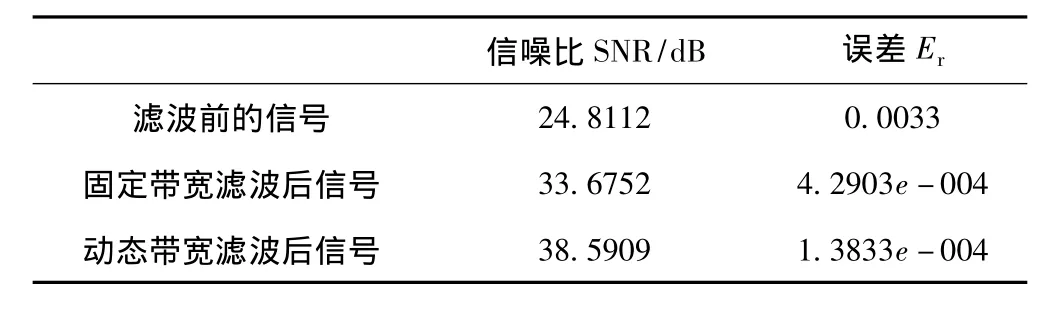
表5 滤波前后效果指标分析

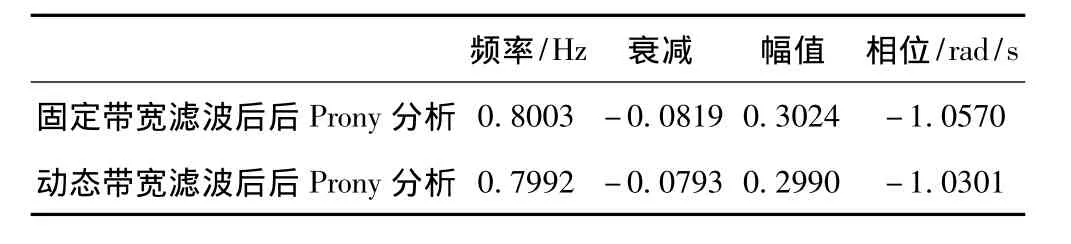
表6 滤波后Prony分析结果

由图10和图11可知，其中蓝线为滤波后信号，红线为加噪前信号，两者重合程度较高，滤波效果较好。由表5、6可知，余弦神经网络方法有效的滤除了随机白噪声，提高了信号的信噪比，提高了Prony法的抗噪性。其中动态带宽滤波效果要好于固定带宽滤波法，这是因为随机白噪声分布在整个频谱上，动态带宽可以滤除低频振荡频率范围内的部分频率点白噪声的影响。

5 结论

采用了一种余弦基神经网络的滤波方法。首先，利用余弦基神经网络逼近低频振荡信号，通过对权值的分析，可确定信号有效带宽范围；然后根据信号带宽进行带通滤波，再将输出信号导入Prony模块分析。分别在脉冲噪声、高频谐波噪声、随机白噪声背景下进行了算例分析，表明了该方法具有较好的滤波效果，对提高Prony法模式识别的准确度具有积极意义。

［1］倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析［M］.北京：清华大学出版社，2002.

［2］鞠平，谢欢，孟远景，等.基于广域测量信息在线辨识低频振荡［J］.中国电机工程学报，2005，25（22）：56 －60.

［3］T.Hiyama，N.Suzuki，T.Funakoshi.On-line Identification of Power System Oscillation Modes By Using Real Time FFT［C］.IEEE PES Winter Meeting，Singapore，2000.

［4］张鹏飞，薛禹胜，张启平.电力系统时变振荡特性的小波脊分析［J］.电力系统自动化，2004，28（16）：32 －35，66.

［5］肖晋宇，谢小荣，胡志祥，等.电力系统低频振荡在线辨识的改进Prony算法［J］.清华大学学报（自然科学版），2004，44（7）：883 －887.

［6］竺炜，唐颖杰，周有庆，等.基于改进Prony算法的电力系统低频振荡模式识别［J］.电网技术，2009，33（5）：44 －47.

［7］王洋，王宁会.基于Prony算法的静电除尘器放电信号分析［J］.中国电机工程学报，2003，23（1）：141 －144.

［8］张贤达.现代信号处理［M］.2版，北京：清华大学出版社，2002.

［9］杨芳，马建伟.基于神经网络自适应滤波的低频振荡Prony分析［J］.中国水轮及电气化，2012，86（4）：32 －37.

［10］李大虎，曹一家.基于模糊滤波和Prony算法的低频振荡模式在线辨识方法［J］.电力系统自动化，2007，31（1）：14 －19.

［11］刘森，赵书强，于赞梅，等.基于小波预处理技术的低频振荡Prony分析［J］.电力自动化设备，2007，27（4）：64 －67.

［12］熊俊杰，邢卫荣，万秋兰.Prony算法的低频振荡主导模式识别东南大学学报（自然科学版）.38（1）：64 －68.

［13］袁杰萍，杨育红.自适应变带宽滤波器的设计和仿真研究［J］.通信技术，2006，23（1）：141 －144.

［14］曾喆昭.神经网络优化方法及其在信息处理中的应用研究［D］.湖南长沙：湖南大学，2008.