自适应模糊决策树算法
2013-07-25王熙照
孙 娟,王熙照
(河北大学数学与计算机学院,河北保定071002)
0 引言
目前最具代表的决策树算法是Quinlan提出的C4.5[1]。模糊决策树算法 (fuzzy decision tree,FDT)是在原有决策树算法的基础上引入模糊集理论,能很好的处理与人的思维有关的不确定性、模糊性。因此,FDT算法在处理连续值属性的数据时具有优势[2-7]。为提高分类准确率,FDT的改进算法主要集中在改进用于建树的启发式和改进推理机制这两个方面,具体算法实现体现在与其他机器学习方法的融合,如应用粗糙集、神经网络、基于示例推理和SVM等方法,从而提高分类精度[6-7]。但无论哪种改进算法都需要对FDT算法共有的主要参数值进行设置。目前,模糊决策树算法中的重要参数取值均是经验设定,这严重影响了模糊决策树算法的预测能力。文[2]使用遗传算法优化每个属性的模糊语言项个数,但是对于其他主要参数值却采用经验设定。粒子群优化 (particle swarm optimization,PSO)算法是一种基于群智能的优化工具,具有深刻的智能背景[8-9]。通常PSO算法比遗传算法运行速度快、算法参数少且易于实现[10]。本文提出使用改进例子群算法自动设定FDT的多个主要参数值的自适应模糊决策树算法 (adaptive fuzzy decision tree algorithm,AFDT)。实验表明该算法能够生成性能更优的模糊决策树;最后,分析了模糊决策树算法主要参数之间存在交互影响关系。
1 基本概念
模糊决策树算法可分为3步,首先是模糊预处理阶段,然后是建树阶段,最后是匹配分类阶段。在建树过程中使用启发式从根向叶子方向选取扩展属性产生模糊决策树。对启发式的改进有代表性的方法有使用信息熵的Fuzzy-ID3算法[3]、针对不确定性的 fuzzy-ambiguty算法[5]和引入粗糙集方法的多种算法[6]。
所有FDT算法都必须进行模糊化预处理,而显著性水平α和每个属性的模糊语言项个数K是必须确定的主要参数。其值直接影响生成的模糊决策树的性能。
定义1设模糊信息系统FIS为一个四元组,FIS=(U,A,V,f),其中,U={x1,x2,…xN}是对象的非空有限集,每个示例 xi=(ai1,ai2,…ais);属性集为 A={A(1),A(2),…,A(s)},其中 K=(k1,k2,…,ks)为属性集 A 的语言项个数集,将每个属性模糊化产生ki个的属性值为模糊化后的语言项,每个语言项对应定义在U中的一个模糊子集表示一个模糊概念。模糊子集可使用隶属函数表示,通常采用三角隶属函数。
1.1 显著性水平α
在模糊集上进行划分生成模糊决策树的过程中,同层属性值所覆盖的例子之间有一定的重叠,会影响扩展属性的选取。模糊集合理论中的α水平截集的引入能在一定程度上减少这种重叠的影响,降低分类的不确定性。FDT算法的建树过程均在给定的显著性水平α的基础上进行。一个示例只有当其相关隶属度大于α时才能划分到某个分支。α取值过低不能降低分类的模糊度,即无法去除不重要的分支,取值过高会使得有用数据丢失,降低模糊决策树的扩展能力[6]。
定义2 设在论域U上的模糊集A∈F(U),其隶属函数 A(u),α∈[0,1]记Aα={u|u∈U,A(u) α}称Aα为A的一个α截集,α称为显著水平。
定义3 对定义在U上的一个模糊条件F和模糊条件集p,p={E1…Ek}在显著水平α上的模糊划分为Pα|Fα={Eα1∩Fα1…Eαk∩Fαk},Eαi是在 α 水平上的条件 Ei,Fαi是在α水平上的条件Fi。
1.2 真实水平β
真实水平β是一个阈值,在产生决策树叶子时起到了重要作用,直接控制模糊决策树叶子的生成[6]。FDT算法产生根结点后,计算作为根节点的属性的每一个非空分枝,计算在该分支上的所有例子分到每个类的分类置信水平,如果置信水平大于真实水平β即作为叶子,否则向下进行分支。β取值过低,生成的决策树偏小,不能概括训练集的规律,决策树的训练准确率低;取值过高,生成的决策树巨大,树的扩展能力低,易产生过拟合现象。因此,过高或过低的β取值都会影响模糊决策树的性能。
模糊决策树算法的显著水平和真实水平起到了预剪枝模糊决策树的作用[11]。这两个参数的取值一般通过经验直接给出,很难为不同数据库确定最优参数值,因此,约束了FDT算法在实际分类问题中的应用。
1.3 模糊决策树算法
定义4 设F(U)为在论域U上的强模糊集,FiF(U)(1 i n)。如果满足下面的条件,则生成模糊决策树T。
(1)模糊决策树的每个结点属于F(U)。
(2)对每个非叶结点N,其子节点组成F(U)的子集记为Γ(即-i(1 i n),Γ =Fi∩N)。
(3)每个叶节点包含一个或多个类信息。
1.4 粒子群算法
设在一个n维的搜索空间中,由m个粒子组成的种群X={X1,…,Xm},其中第i个粒子位置为Xi={xi1,…,xim},微粒i相应的飞行速度V={vi1,…vim},P={pi1,…pim}为微粒i所经历过的最好位置,Pg={pg1,…pgm}为整个粒子群中所有粒子历史中的最好位置。每个粒子按下式改变其速度和位置
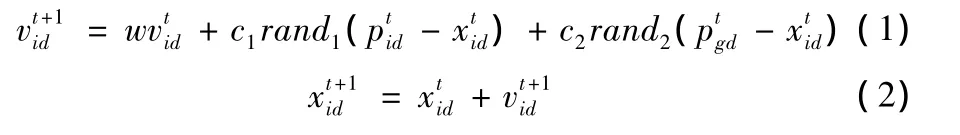
其中d=l,2,…n,i=l,2,…m,m为种群规模,t为当前进化代数,cl和c2为加速常数,w为惯性权重。
2 自适应模糊决策树算法 (AFDT算法)
模糊决策树算法在建树过程中,涉及到一些主要参数值的确定,如果参数值设定不恰当,模糊决策树算法会生成一棵分类能力差的模糊决策树。而本文提出的AFDT算法能通过智能算法自主学习模糊决策树算法中的主要参数值。
2.1 适应度函数的设计
机器学习领域应用智能算法的关键是如何设计适应度函数。多数决策树算法[1-2,12]使用分类准确率作为算法的评价策略,但是剃刀原理更偏向于小的决策树,而扩展能力更是评价树的重要标准[3,11]。因此,只使用分类准确率作为适应度函数的策略不十分充分。本文采用的适应度函数综合考虑了分类准确率,扩展能力和树的规模。
AFDT算法将主要参数α、β和语言项个数集K组成微粒X。微粒Xi被带入建树过程,算法进行模糊化预处理后,使用启发式产生模糊决策树FDTj(1 j m,m为粒子群的规模),其训练准确率为 Trj(xi)、规则数为rulenumj(xi),对测试数据集模糊化后匹配FDTj,其测试准确率为Tej(xi)。Xi的适应度函数定义为
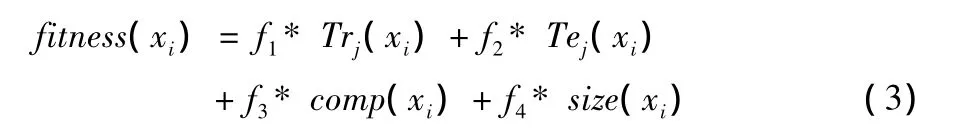
其中 comp(xi)=(Tej(xi)-Trj(xi))/Trj(xi)代表FDTj的概括能力,size(xi)=1÷rulenumj(xi)代表FDTj的大小,fi为比例系数通过搜索适应度的最大值,就能找到性能最优的模糊决策树FDTbest。
2.2 AFDT算法
步骤1 初始化一群微粒X={X1…Xm},其中第i个微粒 Xi包括 xi=(xi1,…xin)T和 vi=(vi1,…vin)T,随机位置xi中的xi1、xi2分别代表随机产生的α和β值,xi3…xin分别代表每个属性的语言项个数(k1,k2,…,ks)。n为每个微粒长度。
步骤2 按式 (3)计算每个微粒Xi的适应度函数值
步骤3 对每个微粒Xi,将当前适应度值与其经历的最好位置pBest的值比较,如果pBest,则判断模糊决策树规则数是否小于pBest保留的规则数,如果小于便更新pBest;否则如果则将其作为当前的最好位置否则不操作。
步骤4 对每个微粒Xi将其适应度值与全局经历最好的位置gBest的值比较,如果则判断rulenum(xi)是否小于gBest保留的规则数,如果小于则更新gBest;否则如果则将其作为当前的最好位置否则不操作。
步骤5 根据式 (4)(5)更新微粒Xi的速度和位置
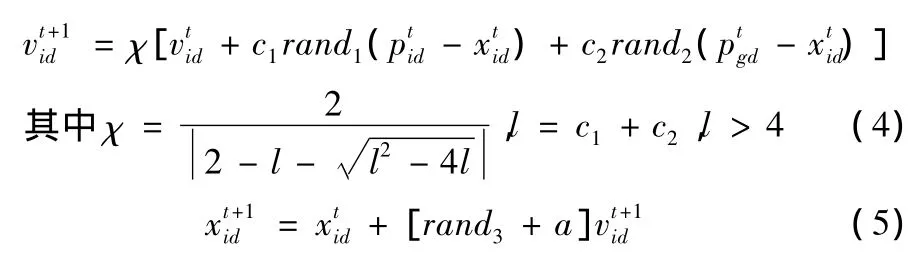
步骤6 未达到最大代数Gmax,则返回步骤2。
对于AFDT算法,一个粒子Xi代表着一组参数值的组合,而在训练矢量空间中,参数组代表着N(N=2+s)个主要参数Xi={xi1,xi2,…,xiN},因此一个粒子Xi包含N维,即Xi∈RN。在解空间中搜索的粒子可以看成N个主要参数在训练矢量空间RN中搜索最优模糊决策树FDTbest的过程。在搜索过程中,一个粒子产生一棵模糊决策树FDTj代表了训练矢量空间中的一个位置矢量Xi,根据公式3计算Xi当前的适应值,即可衡量粒子位置 (模糊决策树性能)的优劣。Vi=(vi1,vi2,…viN)为粒子的飞行速度,即参数值调整的幅度;pBest为本粒子迄今产生的性能最优的模糊决策树,gBest为整个粒子群迄今生成到的最优模糊决策树。式 (4)的第二项代表了粒子对自身的学习,第三项代表粒子间的协作。式 (4)正是粒子根据它上一次迭代的速度、当前位置和自身最好经验与群体最好经验之间的距离来更新速度。然后粒子根据式 (5)飞向新位置,得到新的参数组。
3 算法测试与分析
3.1 实验数据
从UCI数据库中选取10个典型的连续值属性的数据集,使用AFDT算法产生模糊决策树。采用分层旁置法,随机选取70%的数据为训练集,其余为测试集,进行10次无重复实验。AFDT算法确定例子群规模m为20个微粒;每个微粒的长度n取值为2+s;微粒的范围分别是α[0,0.5],β[0,1],ki(1 i s)为 [2,10];最大代数Gmax设定为30代。AFDT算法生成的模糊决策树与使用手工设定的5组参数值生成的5棵模糊决策树进行对比。手工设定参数值的模糊决策树算法使用与AFDT算法相同的语言项个数集K模糊化训练数据。实验结果见表1,其中,MAX(t)列为t=1~5列最高值,α=0.3+t*0.05;β=0.6+t*0.1。
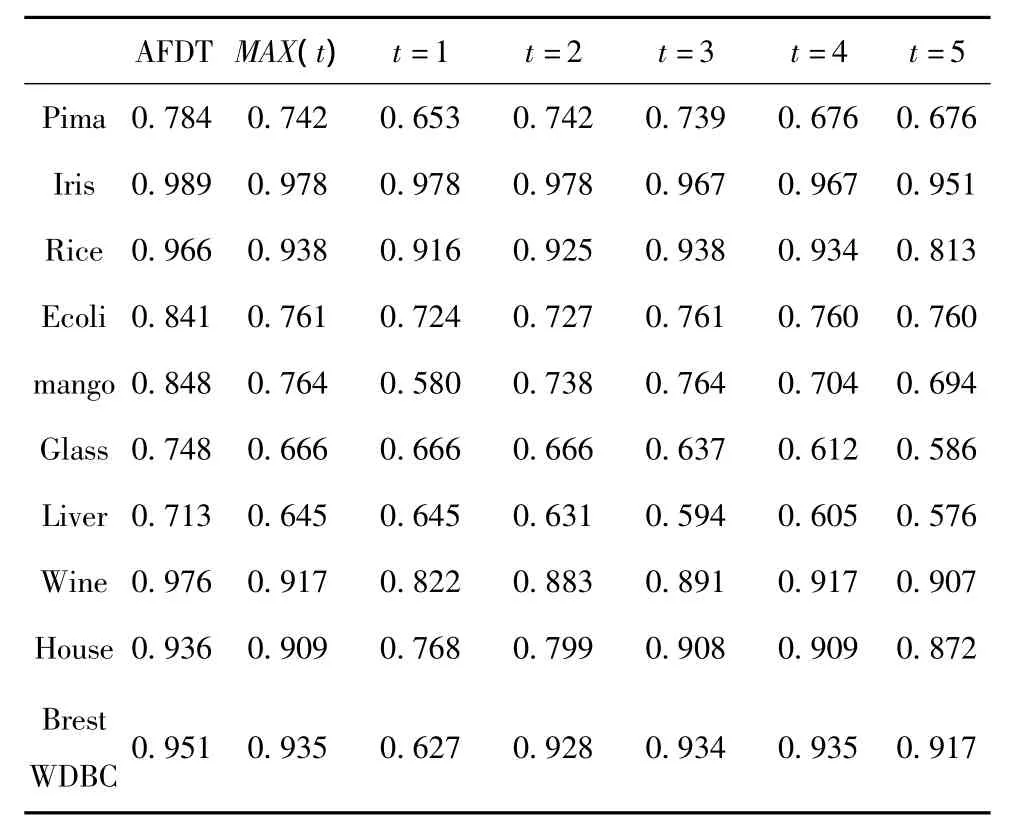
表1 模糊决策树测试准确率平均值比较
表1中可以看出选用不同参数值对模糊决策树的测试准确率影响很大。AFDT算法的测试结果明显高于其他5种参数值设置产生的测试准确率。表1中AFDT的启发式采用信息熵作为选取扩展属性的方法,而使用不确定信息作为启发式得出的实验结果和表1相同。
AFDT算法与已有文献中的实验数据比较见表2使用AFDT算法得到的模糊决策树的性能明显提高,测试准确率几乎均高于经过多种方法改进后的模糊分类算法。这一方面表明参数值的合理设置对FDT算法的重要性另一方面说明使用智能算法选取参数值的必要性。
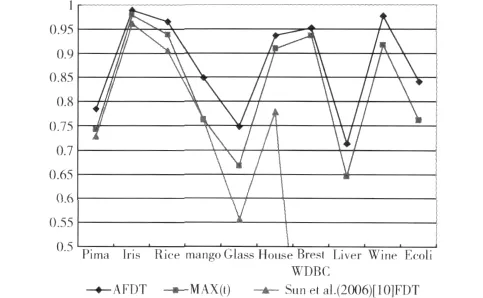
图1 不同参数值产生模糊决策树的测试准确率比较
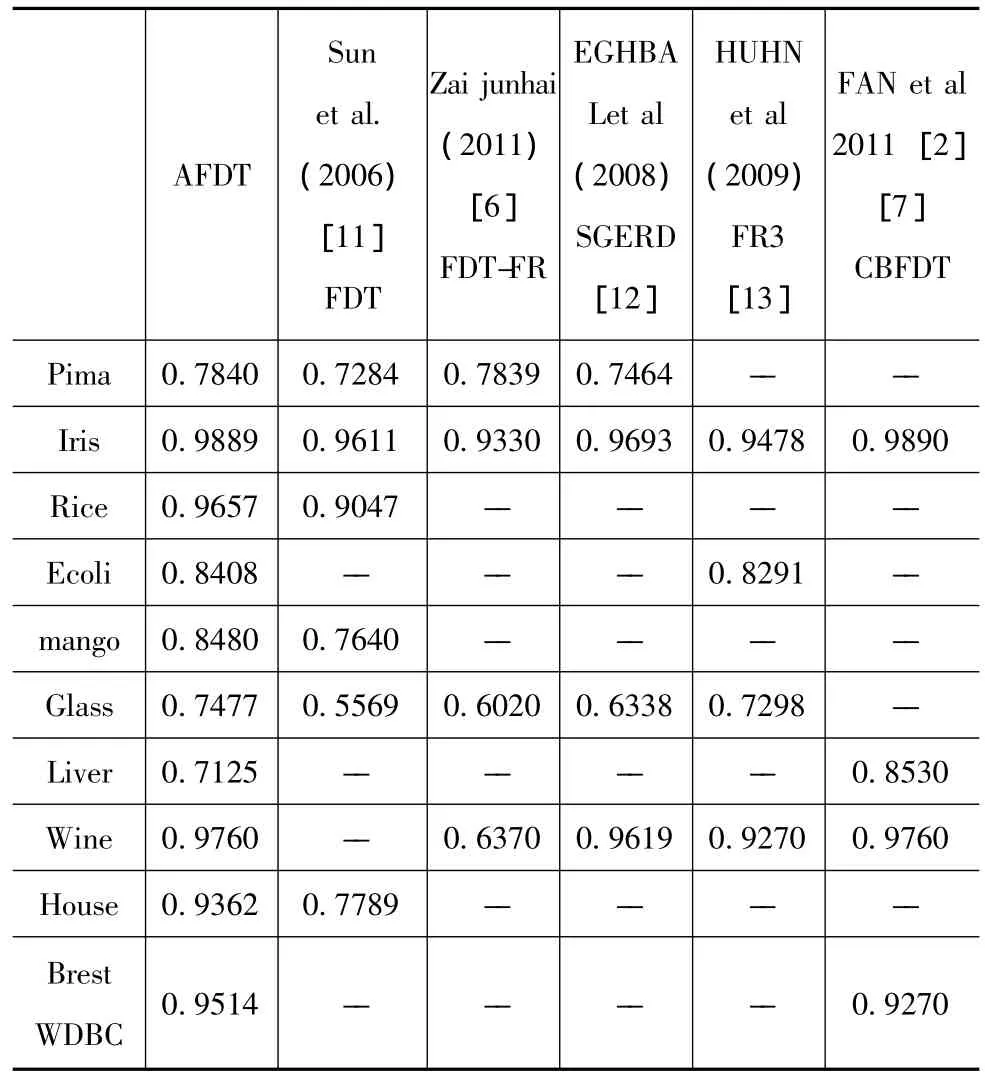
表2 与其他分类算法的测试准确率比较
图1给出3种测试准确率的比较图,第一列为AFDT算法用PSO设定主要参数值、第二列为5组参数值中最优参数值生成的模糊决策树,第三列是文献[11]凭经验设定最优参数值的模糊决策树的准确率。图1中可以明显看出AFDT算法对主要参数进行智能学习后,生成的模糊决策树的预测能力明显提高,特别是对glass数据库,参数值的变化对其性能的影响更为明显。
3.2 参数间交互作用的分析
表3对参数α、β出现的最优域和模糊决策树性能的关系进行分析。
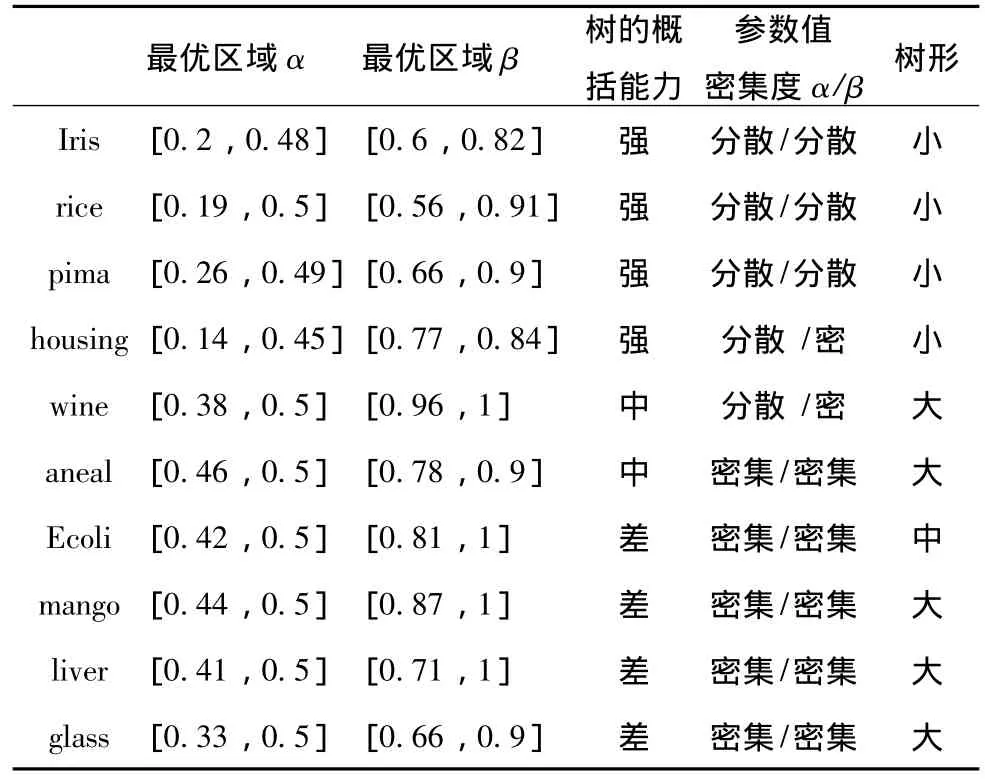
表3 参数α,β优化结果汇总表
其中,概括能力强是指测试准确率高于训练准确率。α、β的密集度指其最优值出现的位置是否临近。树形差别是指最优模糊决策树的规则数是否相差较大。从实验数据中发现:
(1)参数α、β的最优值出现区域均不相同。这说明使用传统的参数值设定方法 (即α取0.4附近,β取0.7附近)是不可行的。
(2)易生成高性能决策树的数据库如iris,rice等,最优参数取值范围较分散,对参数预剪枝的要求不大;而不易产生高性能决策树的数据库如glass,liver等,最优α、β的取值范围集中,即α、β设定的值对FDT算法预剪枝起到关键作用。
(3)从树的扩展能力分析,高性能决策树的扩展能力强,树型变化小,不需要参数α、β干预树的预剪枝,实验数据表现为参数α、β取值范围大、较分散;低性能决策树扩展能力差,树型变化大,需要参数α、β起到预剪枝的功能,实验数据表现为参数α、β取值范围小、密集。
(4)相同训练集、相同初始种群找到的最优参数值α、β不会完全相同。最优参数值出现区域会聚集在几个小区域。在各个小区域中,通常α变化区间小β变化区间大。实验分析发现,在最优小区域中,α找到最优区域取值后,β取值越高产生的决策树越大,但并不能提高训练与测试准确率;β取值越低产生的决策树越小,扩展能力强。α的对应最优区间波动较小 (0.1内波动),β的对应最优区间波动较大 (0.2~0.3内波动)。实验显示,不同数据库的α出现的最优区域不同,且该区域极少出现在α取0.5处,β的最优区域也会在0.6~1之间变化。
3.3 AFDT算法的收敛性分析
粒子群算法具有很好的收敛性。通常AFDT算法学习10代后就可以得到最优解。已经证明决策树算法是NP难问题,因此,粒子群算法易陷入局部最优解的缺陷对AFDT算法的影响很小。图2显示AFDT算法对rice和iris数据库进行50次试验,其适应度平均值的变化情况,可以看出AFDT算法有很好的收敛性。

图2 数据库适应度函数的收敛趋势
4 结束语
本文提出自适应模糊决策树算法用于解决模糊决策树算法中主要参数值的手动设置问题,实验结果表明AFDT算法可以明显提高模糊决策树的概括能力和预测能力。该方法设计的适应度函数有效的在模糊决策树的训练准确率,测试准确率,扩展能力和树的规模四个方面找到了一个权衡。在应用中,AFDT算法可以和任何改进的模糊决策树算法相结合,智能设定其主要参数值,减少经验设定参数造成的低性能,增强了模糊决策树算法的实用性。
[1]AYMERICH F X,ALONSO J,CABANAS M E,et al.Decision tree based fuzzy classifier of1H magnetic resonance spectra from cerebrospinal fluid samples[J].Fuzzy Sets and Systems,2011,170(1):43-63.
[2]FAN Chinyuan,CHANG Peichann,LIN Jyunjie,et al.A hybrid model combining case-based reasoning and fuzzy decision tree for medical data classification[J].Applied Soft Computing,2011,11(1):632-644.
[3]LI Yan,JIANG Dandan,LI Fachao.The application of generating fuzzy ID3 algorithm in performance evaluation[J].Procedia Engineering,2012(29):229-234.
[4]Smith Tsang,Ben Kao,Kevin Y YIP,et al.Decision trees for uncertain data[J].IEEE Transactions on Knowledge and Data Engineering,2001,23(1):64-78.
[5]Mohammad Ebadi,Mohammad Ali Ahmadi,Shahab Gerami,et al.Application fuzzy decision tree analysis for prediction condensate gas ratio:Case study[J].International Journal of Computer Applications,2012,39(8):23-28.
[6]ZHAI Junhai.Fuzzy decision tree based on fuzzy-rough technique[J].Soft Compute,2011(15):1087-1096.
[7]CHANG Peichann,FAN Chinyuan,DZAN Weiyuan.A CBR-based fuzzy decision tree approach for database classification[J].Expert Systems with Applications,2010,37(1):214-225.
[8]Leonardo Vanneschi,Daniele Codecasa,Giancarlo Mauri.A comparative study of four parallel and distributed PSO methods[J].New Generation Computing,2011,29(2):129-161.
[9]ZHANGJianke,LIUSanyang,ZHANGXiaoqing.Improved particle swarm optimization [J].Computer Engineering and design,2007,28(17):4215-4219(in Chinese).[张建科,刘三阳,张晓清.改进的粒子群算法[J].计算机工程与设计,2007,28(17):4215-4219.]
[10]Sudheer Ch,Shashi Mathur.Particle swarm optimization trained neural network for aquifer parameter estimation[J].KSCE Journal of Civil Engineering,2012,16(2):298-307.
[11]SUN Jua,WANG Xizhao.A comparative analysis of rule simplification and pruning fuzzy decision trees[J].Computer Engineering,2006,32(12):210-211(in Chinese).[孙娟,王熙照.规则简化与模糊决策树剪枝的比较[J].计算机工程,2006,32(12):210-211.]
[12]Eghbal G Mansoori,Mansoor J Zolghadri,Seraj D Katebi.SGERD:A steady-state genetic algorithm for extracting fuzzy classification rules from data[J].IEEE Transactions on Fuzzy Systems,2008,16(4):1061-1071.
[13]Jens Huhn,Eyke Hullermeier.FR3:A fuzzy rule learner for inducing reliable classifiers[J].IEEE Transactions on Fuzzy Systems,2009,17(1):138-149.
