挖掘潜在信息 提高应变能力——谈圆锥曲线问题合理解答

☉山东省莱芜市凤城高级中学 张淑敏

一道数学题能否解得顺利、正确，常常取决于是否能发现和利用好题目中的潜在信息，那么潜在信息，潜在哪里？又如何挖掘与利用呢？下面以圆锥曲线问题为例，探讨如下.

一、离开方程 回归定义

焦点和准线繁衍了圆锥曲线一家!焦参数为公有，离心率为分支，学习中应认清共性与个性的统一.

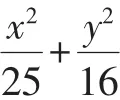
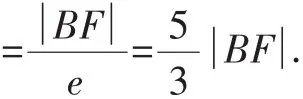
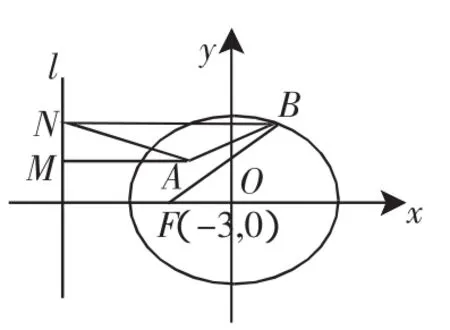
图1

二、规避解析 凸显几何

解析几何具有代数与几何的双重身份，在解题中如果能巧妙利用其几何性质，往往收到意想不到的效果.

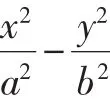
图2

由双曲线的第二定义有

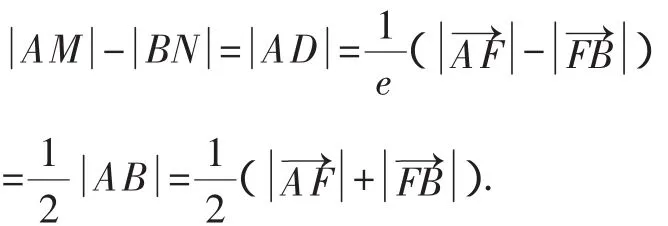
点评：本题解答过程中并未用到方程、坐标系，而是利用双曲线的几何性质与第二定义：到定点与到定直线距离之比为定值（大于1）的点的轨迹是双曲线.由于定义的可逆性，进而从可逆性找到了比例线段，最后用比例关系解出了e的值.

三、定值问题 先定后证

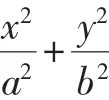
（1）求椭圆C的方程；

（2）过原点O的两条互相垂直的射线与椭圆C分别交于A，B两点，证明：点O到直线AB的距离为定值，并求出这个定值.

解：（1）由题意知4a=8，所以a=2.

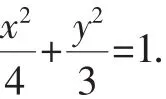
（2）解法1：由题意，当直线AB的斜率不存在，此时可设A（x0，x0），B（x0，-x0）.

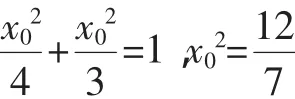
当直线AB的斜率存在时，设直线AB的方程为y=kx+m.

由已知Δ>0.设A（x1，y1），B（x2，y2），所以

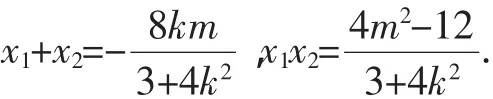
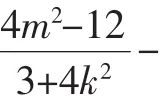
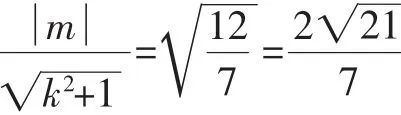
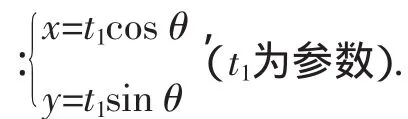
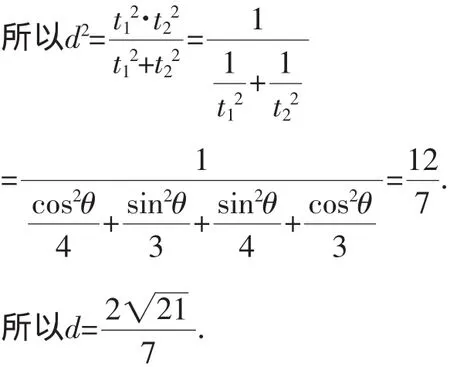
点评：距离既然是定值，那么定值为多少就与参数的取值无关，为此可将直线放在特殊位置，即与x轴垂直，则求出此定值，进而再证明.解法1为通法；解法2考虑到直线参数方程中的几何意义，将直线设为参数方程，亦可简捷求解.

四、最值问题 对称求最

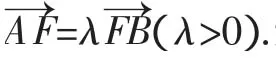
解析：因为抛物线x2=4y关于y轴对称，所以该抛物线的通径、准线等，也关于y轴对称.利用“对称”可以迅速“解得”所求最值.

假设在焦半径FB的端点B（x0，y0）作切线能使△ABM的面积S取得最小值，由于抛物线x2=4y关于y轴对称，所以在焦半径FB的端点B（x0，y0）关于y轴的对称点A（-x0，y0）作切线也能使△ABM的面积S取得最小值.

按对称性，此时的AB就在抛物线的通径上.

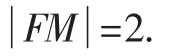
点评：对称图形的最值，也保留着对称性，对称图形的定值也参与对称性之中.在对称位置上寻找最值点，是此类圆锥曲线最值问题的常用策略.

五、垂直问题 问解向量

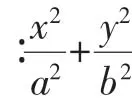
（1）求椭圆C的方程；

（2）若直线l：y=kx+m（k≠0）与椭圆C交于不同的两点M，N（M，N不是左、右顶点），且以MN为直径的圆经过椭圆C的右顶点A.求证：直线l过定点，并求出定点的坐标.

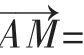
由已知垂直关系，则有（2-x2）（2-x1）+y1y2=0，其中y1y2=（kx1+m）（kx2+m）=k2x1x2+km（x1+x2）+m2，即

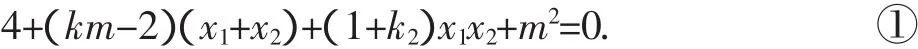
当m+2k=0时直线恒过点（2，0），与点A重合，显然不符合.

点评：平面向量为平面解析几何增添了更加鲜活的生命力，一方面，利用平面向量，可以简洁而清晰地叙述圆锥曲线有关问题的条件和待求解的问题；另一方面，借助平面向量这一工具，也可使有些圆锥曲线垂、夹角问题得到简捷的解法.