基于“阅读·引导·提炼·探究”的教学设计：空间几何体的表面积

☉江苏省南通市小海中学 顾艺玮

一、教材分析

空间几何体的表面积是必修2立体几何初步这章最后一节的内容.此部分内容在高考中不属于重点考查内容，但知识的形成过程中却渗透着数形结合的思想、运动的观点.在本章第一节“空间几何体”中教材从整体观察入手，通过运动的过程引导学生认识柱、锥、台的结构特征，这种运动观点正与它们表面积公式之间的关系相对应，体现了数形结合的思想.柱、锥、台的表面积公式推导不难，重点是体会图和表面积的关系.而且教材中建议联系平面图形的知识，利用类比等方法，理解两者的异同以及内在联系，逐步培养学生的空间想象能力.

二、教学目标

1.了解柱、锥、台表面积计算公式，并能计算一些简单几何体的表面积.

2.（1）由部分到整体，由个别到一般，通过“阅读·引导·提炼·探究”掌握柱、锥、台的表面积之间的关系，体会“数”与“形”的完美结合.（2）通过平面几何和立体几何进行类比，认识类比法，并学会把它用于对问题的发现中，提高学生分析问题、解决问题的能力.

3.让学生感受数学知识间的神奇联系，激发学生学习的兴趣.让学生在问题生成和解决的过程中体验类比、化归等思想方法，提高数学素养，培养创新意识.

三、教学重点

平面几何和立体几何的类比过程，空间几何体表面积的计算.

四、教学难点

运用类比进行猜想.

五、教学方法

阅读·引导·提炼·探究.

六、教学过程

（一）自主阅读，提出问题

阅读材料：平面几何与立体几何的类比.

类比是根据两个对象在某些方面的相同或相似，推出它们在其他方面的相同或相似点的一种推理方法.

由于类比推理所得的结论的真实性并不可靠，因此它不能作为严格的数学推理方法，但是它是提出新问题和获得新发现取之不竭的源泉.

平面几何和立体几何在研究对象和方法、构成图形的基本元素等方面是相同或相似的，因此，在两者之间进行类比是研究它们性质的一种非常有效的方法.［1］

下面就平面几何中三角形、平行四边形、梯形之间的关系与棱锥、棱柱、棱台的关系进行比较.

类比案例1：

方式1：（如图1）

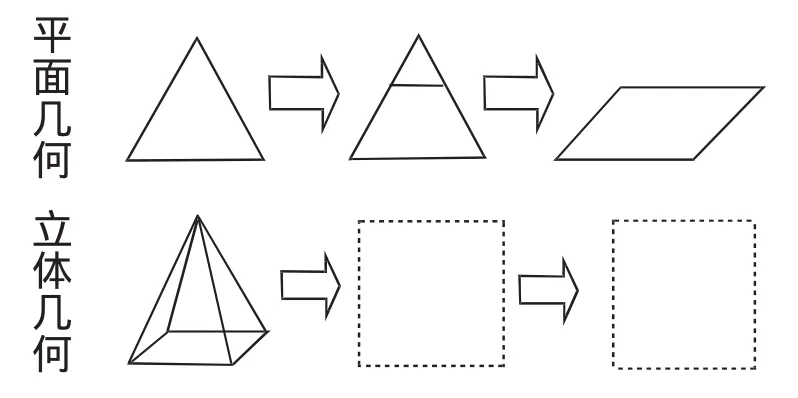
图1

方式2：（如图2）

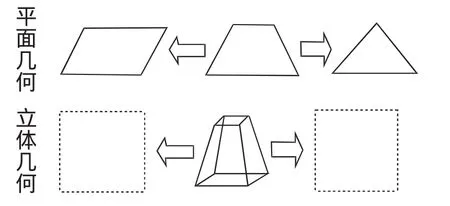
图2

类比案例2：（如图3）

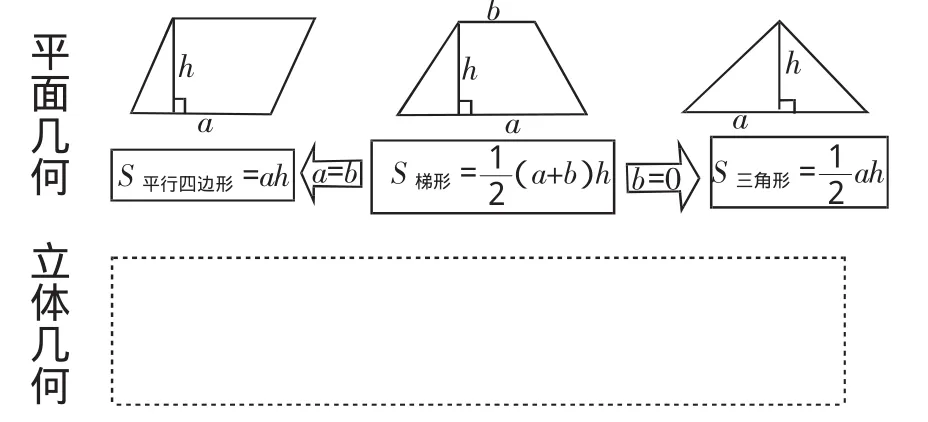
图3

问题1：阅读类比案例1，请在空白处画上合适的立体图形；

问题2：根据类比案例2中平面几何的三个公式的关系，你能提出怎样的猜想？试在立体几何的方框中写下你的猜想，并尝试进行自主探究.

设计意图说明：阅读材料介绍了类比法这种新的学习方法，让课堂的引入别致新颖.材料用运动的思想阐述了三角形、梯形、平行四边形之间的关系，对学生已有的知识进行有意义的改组，为立体几何的研究作好铺垫.案例1从“形”的角度对平面几何与立体几何进行类比，其中两种方式的图形位置进行了调整，其目的是方式1温习这章第一节中柱、锥、台的结构特征，方式2为下面的研究做好准备.案例2是从“数”的角度对立体几何和平面几何的关系进行进一步的诠释和说明，体现了数与形的完美结合.这一切给学生很大的冲击力，激发了他们想继续探索的热情.本堂课选择以阅读材料的形式创设问题情境，充分显示了它的独特性.一方面给学生不一样的视觉感觉，调动了上课气氛，另一方面培养了学生的阅读习惯，以及归纳概括、自主发现的意识.

（二）引导交流，数学活动

通过阅读，学生了解了有关的数学知识，在此基础上教师引导他们共同解决前面的两个问题.通过对问题1的思考，复习空间几何体的形成过程，感受运动观点的合理迁移.问题2的思考则让学生的思维得到发散，他们情绪饱满、各抒己见，使学习过程成为在教师引导下的“再创造”过程.

设计意图说明：通过学生积极主动的讨论及教师适时点拨让学生对平面几何和立体几何的关系有深刻的认识，并积极地猜想结论，为知识的建构做好充分的准备.

（三）自主提炼，数学建构

（1）直棱柱、正棱柱、正棱锥、正棱台的概念.

直棱柱：侧棱和底面垂直的棱柱.

正棱柱：底面是正多边形的直棱柱.

正棱锥：底面是正多边形，顶点在底面的正投影是底面中心的棱锥.

正棱台：正棱锥被平行于底面的平面所截，截面和底面之间的部分.

设计意图说明：遵循从特殊到一般原则，从特殊的柱、锥、台入手进行研究.简单介绍有关概念，归纳其图形的特征，为下面分析它们的侧面积做好铺垫.

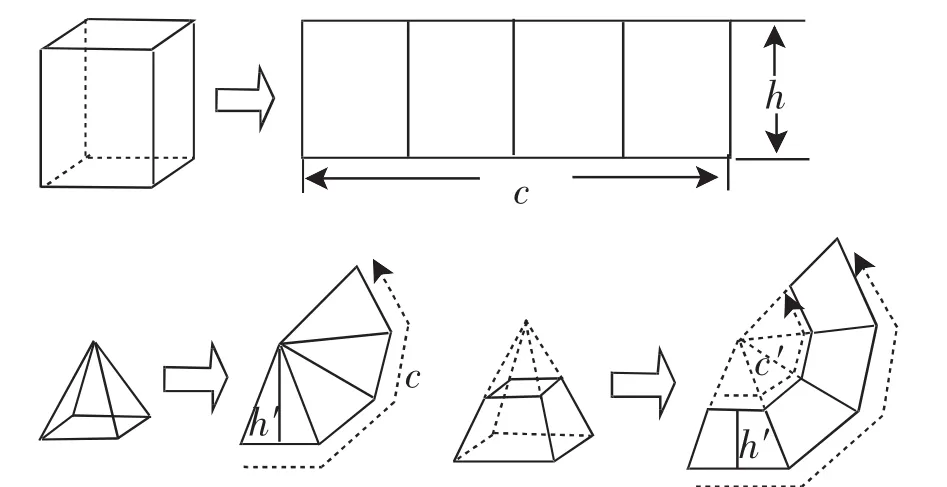
图4

（2）正棱柱、正棱锥、正棱台的侧面展开图（如图4）.问题：正棱柱、正棱锥、正棱台的侧面展开图是什么？设计意图说明：问题的提出有助于理解它们的概念，并培养了学生的空间想象能力.教师可用事先准备好的纸质模型或多媒体课件演示，验证图形的变化，让学生经历观察、想象、验证的过程.

（3）正棱柱、正棱锥、正棱台的侧面积公式.

①正棱柱的侧面积：S正棱柱侧=ch；

直棱柱的侧面积：S直棱柱侧=ch.

思考：正棱柱、正棱锥、正棱台的侧面积公式间的联系与区别（如图5）.

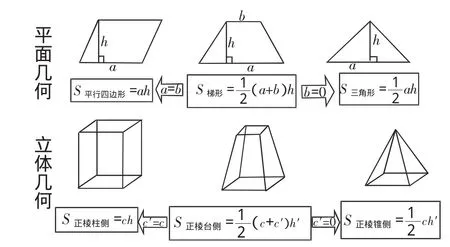
图5

设计意图说明：通过分析讨论柱、锥、台的侧面积之间的关系，体会“数”与“形”的相互交融，提高学生分析、归纳的能力，并且将这种关系与阅读材料上平面几何中的公式进行比较，前后呼应，体现了平面图形和立体图形的内在联系，加强了学生对类比法的认识.

（四）实践探究，数学应用

（1）初步应用.

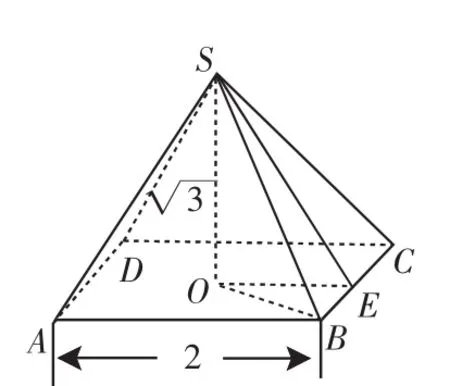
图6

思考：图6中，若连接OB，则在三棱锥S－OBE的表面三角形中，直角三角形共有______个.

设计意图说明：例1的设置是为了巩固空间几何体的表面积公式，注意棱锥的高和斜高的区别与联系.题后的思考则让学生更深入地探究立体几何图形，帮助学生完善思维结构，发展空间想象能力.

（2）深入探究.

圆柱的侧面积：S圆柱侧=2πrl.

问题：你能根据圆柱的侧面积公式猜想圆锥、圆台的侧面积公式吗？

思考：S圆柱侧=2πrl=πl·2r=πl·（r+r），S圆台侧、S圆锥侧（如图7）.

设计意图说明：教材中要求不必讨论圆柱、圆锥、圆台的侧面积公式推导.结合前面的棱柱、棱锥、棱台的内在关系，这里让学生再次经历猜想，用已学过的知识进行归纳和类比，感受知识间的神奇联系，体会数学的奥秘所在.

（3）深入演练.

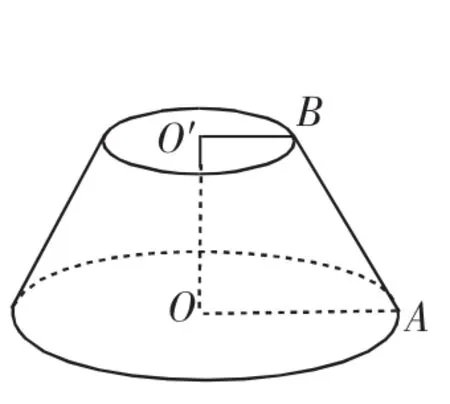
图8

设计意图说明：例2的设置是掌握对旋转体的表面积的计算，进一步巩固上面研究的结论，让学生提高运用知识解决问题的能力.

（五）回顾反思，总结提升

（1）数学知识：

①空间几何体的侧面展开图；

②空间几何体的侧面积的计算公式（如图9）.

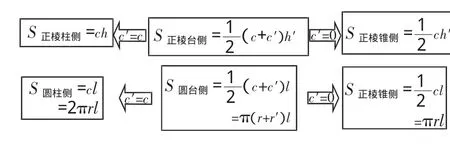
图9

（2）数学方法：阅读、观察、类比、探究.

（3）数学思想：将立体几何问题转化为平面几何问题.

设计意图说明：从知识、方法、思想三个角度进行总结，帮助学生进一步建构知识结构，提炼探究方法，提出新的探究方向，将探究活动延伸到课外.

1.普通高中课程标准实验教科书（必修2）［M］.南京：江苏教育出版社，2012.■