电连接器接触件结构分析与插拔试验

潘 骏 靳方建 陈文华 钱 萍

1.浙江理工大学浙江省机电产品可靠性技术研究重点实验室，杭州，310018

2.杭州航海仪器有限公司，杭州，310024

0 引言

随着航天工程、电子通信工程的发展，电连接器作为传递电信号和电能的基础元件，在系统中的运用越来越广。而实现电连接器连接功能的是集成在电连接器绝缘体内部的多对接触件，任何一对接触件的接触失效都会对整个系统的可靠性造成影响，所以，研究和开发高可靠性的电连接器接触件，对提高系统的可靠性具有至关重要的作用。

据美国对航天失效故障率的统计，由电子元器件引起的故障占40%，而其中大约20%～30%来自电连接器的失效［1］。目前对电连接器接触可靠性的研究，主要集中在建立接触电阻模型、影响因素及失效机理和接触可靠性试验研究等方面［2－6］。通过对其工作环境下的失效模式和失效机理进行分析，并结合可靠性试验，在所建立的统计模型的基础上，对电连接器接触寿命进行评估。

接触件的可靠性取决于接触件的设计、工艺、制造、管理、原材料性能和工作环境等多种因素。因此，分析接触件的结构对接触情况和接触可靠性的影响，对于提高电连接器的可靠性有着重要的意义。文献［7－8］通过理论分析与试验，研究了插针头部不同形状对接触件插拔力的影响，并对插针头部进行了局部优化。文献［9－10］采用有限元仿真与实验相结合的方法，研究了接触面粗糙度对汽车用铜合金电连接器接触件的接触电阻的影响。文献［11］对电连接器中呈结构不对称形状的接触簧片进行了仿真，得到了其根部应力的分布情况，并以根部应力最小为目标函数，进行了结构优化。

但是，针对接触件簧片结构参数对接触情况和可靠性的影响，以及接触件的插拔过程中插拔力变化情况的研究较少。为此，本文对电连接器的接触件结构进行力学分析和接触情况研究；通过有限元仿真，分析各结构参数对接触情况和接触可靠性的影响；并通过插拔试验，研究插拔力随插入过程的实际变化情况，为设计高可靠性的电连接器接触件提供方法和依据。

1 接触件结构力学分析与接触情况研究

1.1 接触件结构力学分析

圆柱式开槽接触件是最常用的电连接器接触件，如图1所示。插针与插孔插合时，依靠插孔簧片结构发生弹性变形产生接触压力。为具体分析簧片结构参数与接触压力的关系，可将圆柱式开槽接触件简化成图2所示的悬臂梁结构（L为悬臂梁长度，δ为挠度，F为接触压力），其产生的接触压力F满足下式：

式中，E为弹性模量；I为横截面的惯性矩。

图1 圆柱式开槽接触件

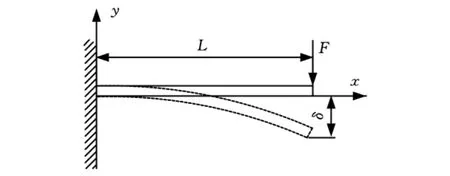
图2 简化悬臂梁模型

插合时，接触件接触面之间的力由两部分组成，如图3所示，其中Ft为摩擦力，Fn为法向接触压力，接触面之间的摩擦因数记为μ，则有Ft＝μFn。插针的插入力记为Fi，则接触件在三个力的作用下达到力学平衡，如图3a所示；进一步根据力学分析可得，插孔弹性变形产生的接触压力F和插入力Fi的关系式如下：

式中，α为摩擦力与接触件轴线的夹角。

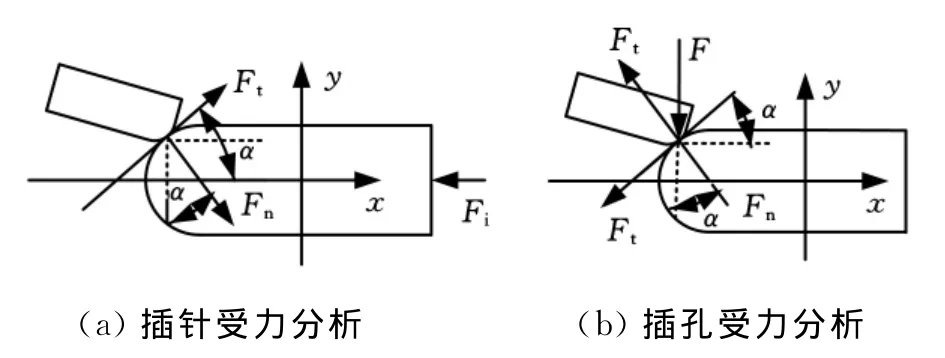
图3 接触件接触简图

用r1和r2分别表示插针头部球体半径和插孔内孔倒角半径，并结合图4进行分析。

α初始值α0为

α随插入量s的变化值为

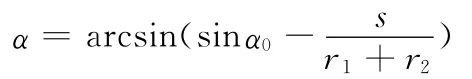
结合图4可以得到，当插入量为s时，插孔产生的挠度为

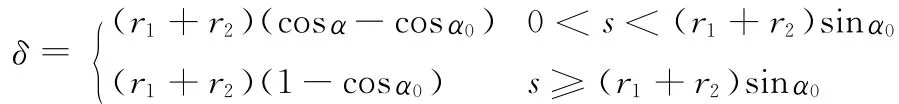
结合式（1）和式（2），可以计算出接触件的插入力随插入量的变化趋势。

图4 插入过程示意图

1.2 接触件接触情况研究

接触件的实际接触情况如图5所示，可根据一般情况的赫兹接触理论［12］对其进行接触面积分析计算，椭圆形接触面积的长短半轴计算公式分别为

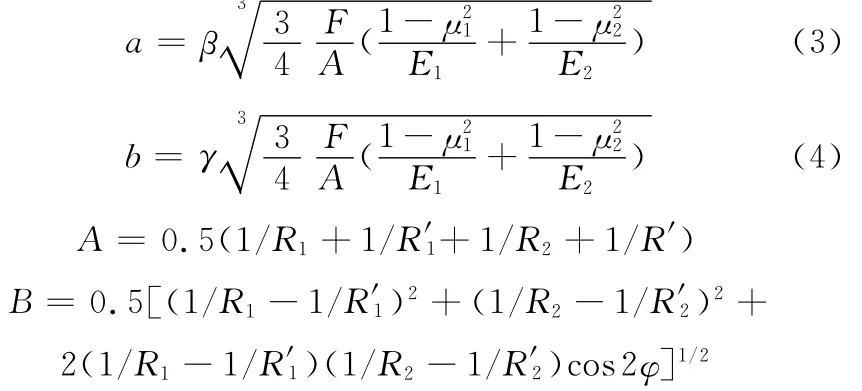
式中，F为接触压力，μ1、μ2分别为两种材料的泊松比；E1、E2分别为两种材料的弹性模量；β、γ为与B/A有关的系

图5 接触件接触简图

对于型号为YF8的分离脱离电连接器中的14＃双片簧接触件（外径为2mm），其尺寸参数为：插孔外半径R＝1mm，内孔半径为r＝0.55mm，开槽长度（即簧片悬臂长度）L＝5mm，开槽宽度为m＝0.5mm，插孔倒角r1＝0.3mm，插针半径r2＝0.5mm；插孔簧片的收口量一般为f＝0.15mm，则在插针完全插入时，插孔簧片产生的挠度为δ＝r2－r＋f＝0.1mm。接触件材料为铍青铜，其中μ1＝μ2＝0.34，E1＝E2＝110GPa。从而可计算得：长轴2a＝0.2426mm，短轴2b＝0.0373mm。

因为b≪a，与实际接触情况不符合，需对b的计算结果进行修正。若将a的值作为固定值，可将接触模型进一步简化为两个圆柱正交的形式，如图6所示。对于该特殊的接触模型，可得到更简单的接触椭圆方程为

式中，C为常数。

根据上文取值，R2＝r1＝0.3mm，R1＝r2＝0.5mm。考虑到实际接触情况，应有a＞b，故

由此可得：2b＝0.1456mm。

参数a和b是通过两步计算出来的，一致性差，为解决该问题，可假设参数b已知的情况下，将模型进一步简化为图7所示的模型，即相互平行的圆柱体和圆柱凹面接触的形式，圆柱长度为2b。同样，按照赫兹接触理论，可得接触面的接触尺寸关系式为

式中，p为线载荷密度，p＝F/（2b）。

同样，可求得2a＝0.1682mm。

为得到比较稳定的长短轴值，可对上述接触模型分析计算过程进行循环求解，迭代的结果为：2a＝0.1911mm，2b＝0.1140mm。

图6 横截面简化模型

图7 纵截面简化模型

经过插合的接触件，在接触表面会留下磨损痕迹，观测痕迹的情况，即可得到接触面积的实际情况。图8所示为上述14＃插孔和插针，经过多次插合后，其稳定的磨损痕迹在电镜下的观测结果；其中明亮斑点是接触点，可以看出明亮斑点近似椭圆形，长轴大约为0.2mm，短轴大约为0.1mm，这与上述计算方法的计算结果接近。

图8 插拔多次后接触情况电镜图

2 电连接器接触件有限元仿真分析

以上述14＃接触件为仿真对象，由于接触件为对称结构，取插针和插孔头部结构的1/4（每个簧片的1/2）进行建模，结果如图9所示。

图9 接触件简化建模结果

根据上述材料参数，设置材料的弹性模量和泊松比。设定插孔的内表面和倒角面为接触面，设定插针的圆柱面和头部球面为目标面。接触类型为非对称摩擦接触，摩擦因数为0.13。采用高阶三维十节点的Solid 187实体单元对模型进行网格划分。为保证计算精度和收敛性，接触面的网格划分相对较密，划分结果如图10和图11所示。

图10 插针网格划分结果

图11 插孔网格划分结果

因为不计惯性力和阻尼，所以采用非线性的静态结构仿真模块进行仿真，且计算过程选择为大变形分析。在插孔的根部施加固定约束，在插针顶部施加一个轴向的插入位移，在插针和插孔的对称面上施加无摩擦对称约束。根据结构分析，插拔力在插合的过程中会出现一个峰值，为保证收敛性，结合出现峰值的位置将载荷步分为两步，两子载荷步位移大小均为0.35mm。

图12所示为接触件插合时接触情况的仿真结果，由于只选取插孔簧片的1/2进行建模，所以可以看出接触区域近似1/2椭圆形，与上述观测结果相吻合。仿真结果中接触区域的长短轴大小如图12b所示，长轴结果接近0.2mm，短轴结果接近0.1mm，与电镜下的观测结果接近。

在对接触件材料进行强度分析时采用第四强度理论，应力对应为有限元软件里面的等效应力。图13所示为插孔簧片整体应力和簧片根部的应力分布情况。从图中可以看出，在根部的边缘部位应力较大，接近或超过材料的屈服极限280MPa，材料将发生塑性变形。但是，图中应力较大的部分所占比例较小，仅为根部边缘的结构突变部分；且从图中可以看出，在边缘处应力等高线较为密集，说明应力变化较快，这是由于应力集中造成的，在设计过程中应尽可能减少该现象的发生。

图12 接触区域的位置及形状仿真结果

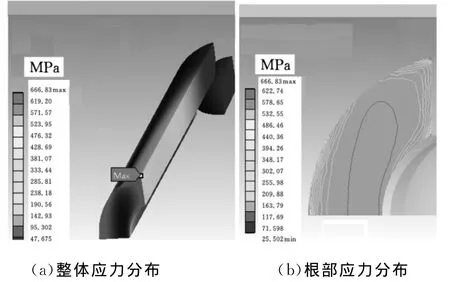
图13 插孔簧片整体应力和根部应力分布

图14所示为接触件应力和簧片根部应力分布的非线性材料仿真结果，簧片根部应力的最大值为289.26MPa，大于材料的屈服极限280MPa，边缘部位的材料已经发生塑性变形；但结合应力云图中的等高线，基本上其他部位应力均小于材料屈服极限，材料均未发生塑性变形。

由于接触压力测量比较困难，故经常通过插拔力来间接判断接触压力。图15为接触压力随插入量的变化趋势图。由图可见，三次计算结果的变化趋势相同，且偏差较小，这说明根部的塑性变形对接触件的接触压力影响较小。接触压力的稳定值出现在插针头部刚好完全插入以后，即大约在0.35～0.4mm 处。在插入量大于0.4mm时，接触压力稳定，说明插针的头部已全部进入插孔内部。考虑了材料非线性的接触压力仿真结果相对较小，这是由于接触件簧片的根部发生了塑性变形。由于插孔倒角的存在，插孔的有效悬臂长度减小，而结构分析过程中，假定悬臂长度不变，所以计算结果较弹性仿真分析结果略小。

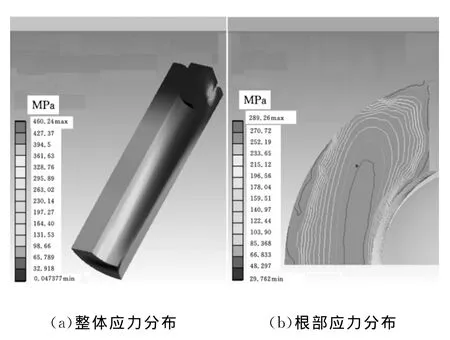
图14 插孔簧片应力的非线性材料仿真结果

图15 接触压力的仿真结果与理论结果对比

图16所示为插入力随插入量的变化趋势，对于三种分析结果，可得到与接触压力基本相同的对比效果；但插入力的最大值出现在插入量约为0.2mm处。接触件在插合过程中，塑性变形对接触件的接触面有一定的影响，所以塑性分析的最大插入力较大。

图16 插入力的仿真结果与理论结果对比

为分析各尺寸参数对接触情况的具体影响程度，表1给出了各尺寸参数对输出参数指标的局部灵敏度。可以看出，插孔簧片长度和厚度对最大插入力、插入力稳定值和接触面应变均有较大的影响，只是它们与参数的相关性相反。收口量对结果参数也有明显的影响，且为正相关，但收口量过大会造成加工时根部应力集中和残余应力严重，影响接触可靠性，所以要尽可能地减小收口量。开槽宽度对接触件的最大插入力、插入力稳定值和接触面应变也有一定的影响，但插孔倒角对接触件的接触性能影响较小，可以结合实际加工情况进行选取。各结构参数对插拔力的灵敏度相对较高，即对结果的影响主要表现在对最大插入力和插入力稳定值的影响上。

表1 各尺寸参数对结果指标的局部灵敏度

3 接触件插拔试验与结果分析

为与上述理论分析和仿真结果进行对比，对型号为YF8的电连接器中14＃双簧片接触件（φ2mm）进行插拔试验。图17所示为插拔力试验结果，插拔力在插入过程中的变化趋势与前面的理论分析和仿真结果相一致。试验结果中的插入力最大值也是出现在插入量大约为0.2mm处，最大插入力为4.56N；同样在插头全部进入插孔时，插拔力趋于稳定值2.03N。

图17 插入力试验结果

接触压力与摩擦因数无关，仅与接触件簧片的变形有关，通过理论计算得到的接触件接触压力稳定值为7.72N；结合试验得到的插入力稳定值，可得到接触件间的摩擦因数为0.1295。现将仿真分析时的摩擦因数更正为0.1295，重新进行有限元仿真。同样由于摩擦因数对接触压力没有影响，其仿真结果和上述相同，而得到的接触件插拔力的试验结果、仿真结果和理论计算结果对比如图18所示，试验结果与塑性仿真结果最接近。

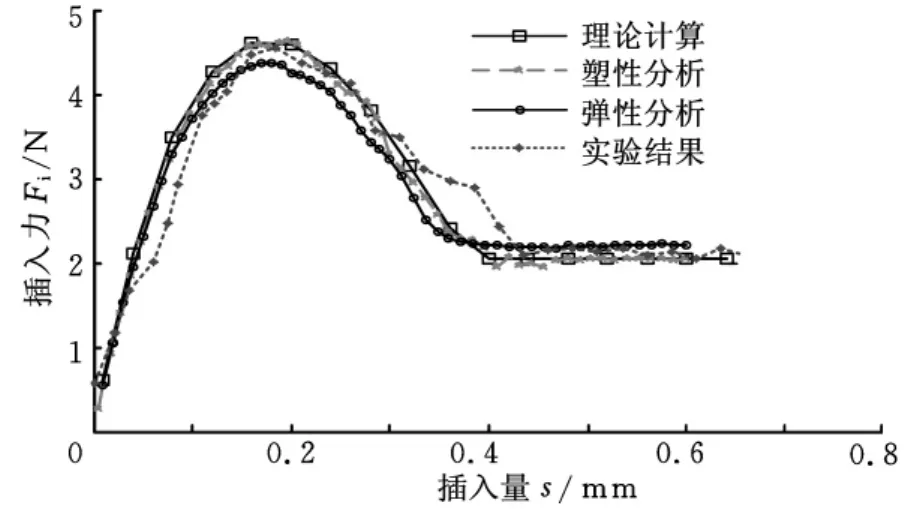
图18 插入力试验结果与仿真结果对比

4 结论

（1）本文以电连接器接触件为研究对象，对接触件结构进行了力学分析，建立了接触压力、插拔力接触件与结构参数之间的关系；基于赫兹接触理论，提出了接触件接触面积的迭代计算方法，提高了计算精度，为进行接触件的接触情况分析提供了理论依据。

（2）建立了接触件的参数化有限元接触模型，并利用ANSYS软件对接触件的插拔过程进行了运动仿真，分析了接触件的应力分布情况；通过对接触件各个关键参数的参数化，得到了各参数对接触情况影响的灵敏度，确定了影响接触件接触性能的关键参数，为接触件结构的优化设计提供了依据。

（3）对接触件进行了插拔试验，分析了接触件插入过程中插拔力的变化情况，与理论分析和仿真结果进行了对比；验证了提出的理论分析、仿真计算方法的可行性，为设计高可靠性的电连接器接触件提供了依据。

［1］杨奋为.军用电连接器的应用与发展［J］.机电元件，2012（4）：52－61.

Yang Fenwei.Discussion on Innovation and Development of the Military Electrical Connector［J］.Electromechanical Components，2012（4）：52－61.

［2］Chen Wenhua，Liu Juan，Gao Liang，et al.Accelerated Degradation Reliability Modeling and Test Data Statistical Analysis of Aerospace Electrical Connector［J］.Chinese Journal of Mechanical Engineering，2011，24（6）：957－962.

［3］潘骏，刘红杰，陈文华，等.基于步进加速退化试验的航天电连接器接触可靠性评估［J］.中国机械工程，2011，22（10）：1197－1200.

Pan Jun，Liu Hongjie，Chen Wenhua，et al.Contact Reliability Assessment of Aerospace Electrical Connector Based on Step－up－stress Accelerated Degradation Testing［J］.China Mechanical Engineering，2011，22（10）：1197－1200.

［4］Timsit R S.Electrical Contact Resistance：Properties of Stationary Interfaces［J］.IEEE Transactions on Components and Packaging Technologies，1999，22（1）：85－98.

［5］Li Zhigang，Jiang Dong，Li Wenhua，et al.Reliability Analysis and Failure Prediction Study of Dynamic Contact Resistance on Contact［C］//Proceedings of 48th IEEE Holm Conference Electrical Contacts.Orlando：IEEE，2002：61－65.

［6］钱萍.航天电连接器综合应力加速寿命试验与统计分析的研究［D］.杭州：浙江大学，2010.

［7］Horn J，Egenolf B.Shape Optimization of Connector Contacts for Reduced Wear and Reduced Insertion Force［J］.AMP Journal of Technology，1992，2：42－46.

［8］Sawchyn I，Sproles E J.Optimizing Force and Geometry Parameters in Design of Reduced Insertion Force Connectors［J］.IEEE Transactions on Components，Hybrids，and Manufacturing Technology，1992，15（6）：1025－1033.

［9］Beloufa A，Mastorakis N E，Martin O.Influence of Shapes，Contact Forces and High Copper Alloys on the Contact Resistance and Temperature［C］//the 2nd WSEAS International Conference on Engineering Mechanics，Structures and Engineering Geology.Rodos，Greece：EMESEG，2010：139－144.

［10］Beloufa A.Numerical and Experimental Optimization of Mechanical Stress，Contact Temperature and Electrical Contact Resistance of Power Automotive Connector［J］.International Journal of Mechanics，2010，4（4）：94－104.

［11］Hsu Yeh－Liang，Hsu Yuan－Chan，Hsu Ming－Sho.Shape Optimal Design of Contact Springs of Electronic Connectors［J］.Journal of Electronic Packaging，2002，124：178－183.

［12］陈国荣.弹性力学［M］.南京：河海大学出版社，2002.