超声切割刀动力学分析和结构优化设计

周胜利 姚志远 沙 金

南京航空航天大学机械结构力学及控制国家重点实验室，南京，210016

0 引言

超声切割是利用超声发生器使切割设备做超声频率的振动，通过刀头将碰撞和冲击能量传递到被切介质，致使被切介质材料疲劳破碎而达到切割目的的一项新型工艺技术。超声切割可更有效、更精确地加工如碳纤维、玻璃纤维、凯夫拉纤维、各种蜂窝材料等航空制造领域所用的复合材料和硬脆材料如光学玻璃、硅晶体、陶瓷等［1－2］。另外，由于与生物组织接触的金属刀头以一定的超声频率振动时可使生物组织内水汽化、蛋白氢键断裂、细胞崩解、组织被切开、凝固和封闭小血管，所以超声切割技术又可运用到手术工具上，制成切割止血刀，已在国内外得到了广泛的应用［3－5］。

现阶段超声切割技术的研究多在于新型切割设备的设计和实验研究，以及利用有限元软件进行仿真分析等。在国外，Andreas等［6］设计并研究了一种新颖的多刀片切割装备；Nath等［7］做了超声切割低合金钢的实验研究；Eggers等［8］做了超声切割应用在骨切割和面部手术上的实验研究。在国内，郭玉泉等［9］进行了超声切割用压电换能器的理论研究及有限元仿真；刘井权等［10］进行了超声刀切割系统的模态分析；沙金等［11］研制了一种新型的超声切割刀，并研究了刀头材料对切割力的影响等。

目前，超声切割刀的动力学理论建模研究落后于其结构设计。超声切割刀的结构主体是兰杰文振子［12－15］。对于兰杰文振子，现阶段多是利用ANSYS等有限元软件进行仿真分析，得不到其解析解，因而不能定性地分析结构的物理和几何因素对其输出性能的影响规律。另外，ANSYS计算比较花费时间，对计算结果还需进行模态识别，并且对非线性变截面体进行网格划分时的效果也不太理想，有时甚至会造成程序无法运行。为放大刀头处的振幅，切割刀的结构中引入了变幅杆。变幅杆的声学特性已得到了广泛的研究，并有许多行之有效的计算方法，如传统解析法、等效电路法、替代法、传输矩阵法和有限元法等［16－18］。超声切割刀至少具有两种材料，即压电陶瓷和金属材料，工作时压电陶瓷是激励源，存在着机电耦合问题。因此，切割刀的动力学理论建模还有待于进一步完善。

为优化切割刀性能，有必要对切割刀进行结构优化设计。以往的优化设计也是借助于有限元分析完成的，一样存在着诸如计算时间长，非线性变截面不易处理等问题。本文针对沙金研制的超声切割刀，建立了其振动的动力学模型，得到解析解；在解析解的基础上设计了切割刀的结构优化算法，利用MATLAB编写程序并设计可视化界面。该优化程序运行速度快，优化结果准确，方便了该型切割刀的结构设计。

1 超声切割刀结构

该超声切割刀结构如图1a所示，各部分由45钢建立的螺栓连接在一起。以后端块底部中孔的圆心为原点，建立的该切割刀整体坐标系如图1b所示。

图1 切割刀结构及整体坐标系

其中，第（2）部分压电陶瓷的横截面是带有中孔的矩形，第（6）部分采用了指数截面型变幅杆的设计。忽略电极片，则切割刀可分为六部分，其各部分的截面坐标如图2所示。其中Ⅰ、Ⅲ、Ⅴ为45钢构成的长方体，Ⅱ、Ⅳ虚线部分是半径为r的45钢螺栓，外围是压电陶瓷，Ⅵ在宽度（z）方向为变截面体，沿高度（y）方向是等高度的，其高度为h。Ⅵ在宽度方向的曲线函数为

图2 切割刀各部分截面图

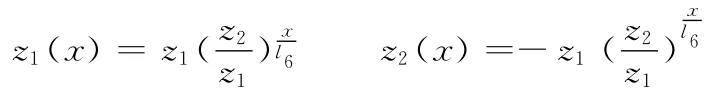
2 结构动力学分析

2.1 结构动力学模型

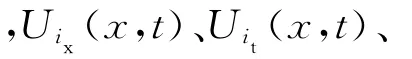
式中，ρ和E分别为45钢的密度和弹性模量；c为切割刀单位体积的等效黏性阻尼系数。

Ⅱ、Ⅳ部分的振动微分方程为

式中，ρt、s11、e33和lt分别为压电陶瓷的密度、弹性柔度矩阵元素、压电常数矩阵元素和厚度。

Ⅵ部分的振动微分方程为

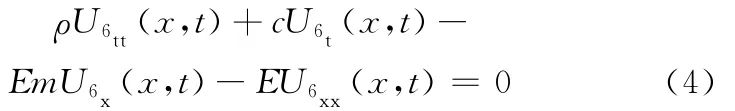
由自由初始条件及切割刀在振动过程中各截面两端位移、应力相等有下列边界条件：

2.2 一阶纵振模态求解

本文切割刀采用一阶纵振为工作模态，在不考虑阻尼和激励的前提下，其式（1）、式（2）、式（4）变为

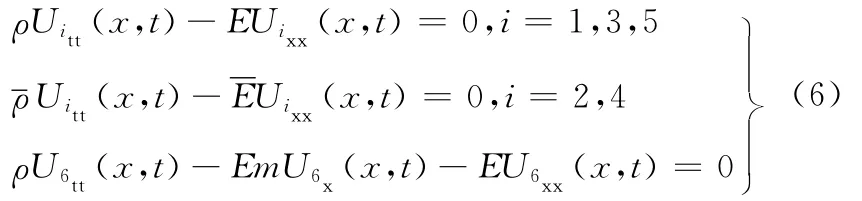
式（6）的解都可写成

由式（5）和式（7）可得一个由12个方程组成的方程组，写成矩阵形式和稀疏矩阵形式则有

式（8）有非零解的充要条件是如下的频散方程：

由式（9）即可求得本文切割刀的一阶纵振频率。

本文超声切割刀的结构参数如表1所示。其45钢和压电陶瓷的材料性能参数如表2所示。

表1 超声切割刀的结构参数 mm

表2 材料的性能参数

将上述参数代入式（9），即可得到一阶纵振频率为52.5k Hz，利用 ANSYS计算的结果为52.3k Hz，利用德国Polytec公司PSV2300F2B型高频扫描激光测振系统测定的结果为53.5k Hz。由此验证了本文算法是准确的。利用本文算法，用MATLAB编程计算一阶纵振频率仅需2s左右，而利用ANSYS计算一阶纵振频率需要数分钟。在计算出纵振频率的基础上，很容易按最大振幅归一化画出切割刀一阶纵振振型图并找出节面所在位置，如图3所示，图中A为振幅，Amax为最大振幅。

图3 切割刀一阶纵振振型图

3 结构优化设计

3.1 结构优化数学模型

为使压电陶瓷的激振效果达到最大和使夹持件对切割刀振动的影响达到最小，需将压电陶瓷和夹持件放置在切割刀的节面处［19］。由于该切割刀压电陶瓷对称分布在夹持件的两侧，所以该切割刀结构优化目标为

式中，lc为夹持件中心位置；ld为切割刀节面位置；ε为允许偏差。

由振动理论可知，对切割刀节面位置影响最大的因素为前后端块和变截面部分的长度，考虑到前后端块较易加工，选取前后端块长度作为优化参数，分别设为lq和lh。综上，本文切割刀结构优化设计的数学模型可描述为

满足条件：

为了满足超声要求，规定切割刀一阶纵振频率fgz≥20 000Hz。

3.2 结构优化程序

利用MATLAB编写程序，算法如下：

（1）输入参数，设定总长度的搜索步长ΔL。

（4）若Pc（k，j）＝｜lc（k，j）－ld（k，j）｜≤ε，输出L（k）、lq（k，j）、lh（k，j）、fgz（k，j）、Pc（k，j）和振型图；若Pc（k，j）＞ε，则j←j＋1。

（5）若对固定的k，一切lq（k，j）都有Pc（k，j）＞ε，则k←k＋1。

（6）若对一切的k、j都有Pc（k，j）＞ε，则输出；无合适的尺寸，则更改总长度范围或允许偏差。

为 加 工 方 便， 取 ΔL＝ 0.2mm，Δlq＝0.1mm。算 法 第 （2）步 中 估 计lq（k）、lh（k）及fgz（k）的范围是为了减少循环的步数，以节省计算时间。其估计的方法如下：

（1）若变截面部分为等截面长方体，则根据振动理论，节面位置应在切割刀中心处，故有

式中，nt为压电陶瓷片数；ljc为夹持件厚度。

（2）若变截面部分对切割刀的振动无影响，则节面位置应在除去变截面部分以外部分的中心处，故

式中，lb为变截面部分长度。

（3）由步骤（1）、步骤（2）易知lh的取值范围为

（4）因为lq＝L－lh－ntlt－ljc－lb，所以lq的取值范围为

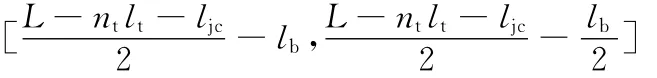
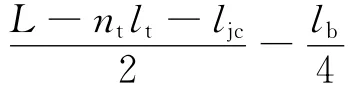
利用MATLAB的GUIDE工具设计人机交互界面并对以上切割刀进行结构优化，选取的总长度区间为［50，52］mm，允许偏差为1μm，优化结果如图4所示。

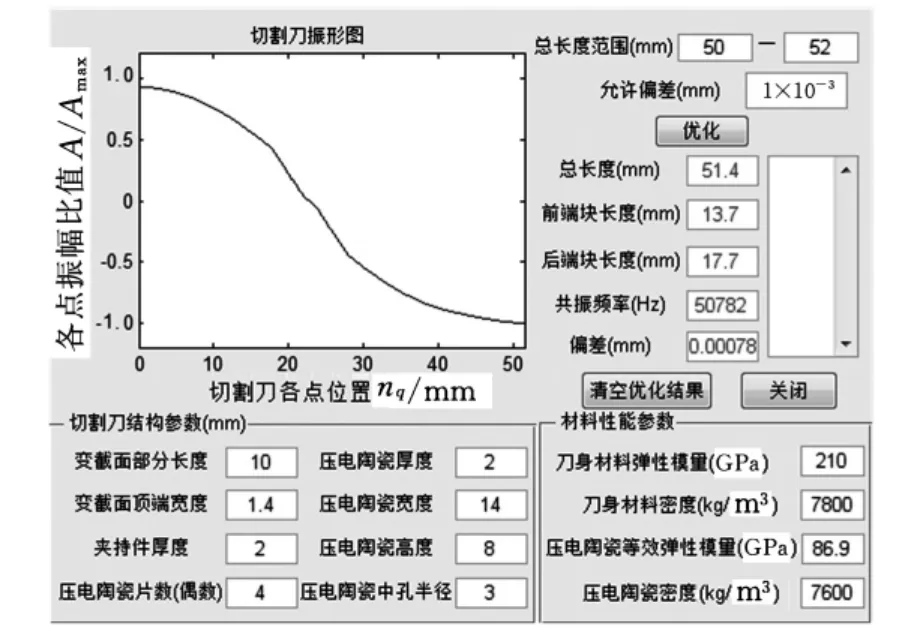
图4 优化结果

经优化，切割刀总长度为51.4mm，前端块长度为13.7mm，后端块长度为17.7mm，一阶纵振频率为50.8k Hz，偏差为0.78μm，达到了优化目标，计算时间约为100s。以上述结构尺寸加工的样刀的一阶纵振频率为50.6k Hz，在相同的80V正弦信号的激励下，优化后的切割刀谐振阻抗为320Ω，振幅为1.4μm，而优化前的切割刀振幅为1.1μm，振幅提高约27%。

4 结语

利用振动理论，建立了超声切割刀的动力学模型，并据模型整理得到其一阶纵振频率和振型的解析式。据解析式计算得到的振动频率52.5k Hz与ANSYS计算的52.3k Hz及实验测试的53.5k Hz相吻合，验证了本文算法的有效性。建立了超声切割刀的优化模型，提出了结构优化算法，并利用MATLAB设计了人机交互优化界面。利用本文算法进行结构优化设计，运行速度快，所耗机时少，优化结果良好，节面位置与夹持件中心位置的偏差在1μm之内，在相同的80V正弦信号的激励下，优化后的切割刀振幅比优化前的切割刀振幅提高了约27%，解决了结构优化难题。本文算法稍作修改后，亦可用于解决具有锥形变截面、双曲线变截面的切割刀的动力学分析及结构优化设计问题。并对超声电机的定子设计具有参考借鉴作用。

［1］刘井权，闫久春，杨士勤.碳纤维预浸料超声切割工艺［J］.焊接，2011（8）：24－26.

Liu Jingquan，Yan Jiuchun，Yang Shiqin.Ultrasonic Cutting Technology for Carbon Fibre Pre－preg［J］.Welding and Joining，2011（8）：24－26.

［2］文立伟，严飙，肖军.复合材料超声切割系统及稳定性研究［J］.复合材料自动化制造技术，2010（17）：49－52.

Wen Liwei，Yan Biao，Xiao Jun.Research on Ultrasonic Cutter System and Stability of Composites［J］.Aeronautical Manufacturing Technology，2010（17）：49－52.

［3］Robiony M，Pplini F，Costa F.Ultrasonic Bone Cutting for Surgically Assisted Rapid Maxillary Expansion under Local Anesthesia［J］.Int.J.Oral Maxillofac，2007，36：267－269.

［4］房爱玲.体外肿瘤治疗设备—超声切割止血刀［J］.中国医疗器械信息，2009，15（7）：26－28.

Fang Ailing.In Vitro Treatment of Tumor：Ultrasonic Scalpel［J］.China Medical Device Information，2009，15（7）：26－28.

［5］宋立为，李晓亮，苏庆.超声切割止血刀与高强度聚焦超声刀的比较［J］.医疗设备信息，2007，22（10）：32－34.

Song Liwei，Li Xiaoliang，Su Qing.Comparison between UHS and HIFU［J］.Information of Medical Equipment，2007，22（10）：32－34.

［6］Andreas C，Margaret L，Matthew C.A Novel Multiple Blade Ultrasonic Cutting Device［J］.Ultrasonics，2004，42：69－74.

［7］Nath C，Rahman M.A Study on Ultrasonic Vibration Cutting of Low Alloy Steel［J］.Journal of Materials Processing Technology，2007（192/193）：159－165.

［8］Eggers G，Klein J，Blank J.Piezosurgery：an Ultrasound Device for Cutting Bone and Its Use and Limitations in Maxillofacial Surgery［J］.British Journal of Oral and Maxillofacial Surgery，2004，42：451－453.

［9］郭玉泉，张辽远.超声切割用压电换能器理论设计及有限元仿真［J］.现代机械，2008（6）：44－46.

Guo Yuquan，Zhang Liaoyuan.Design and Finite Element Simulation on Piezoelectric Ceramic Actuator for Ultrasonic Vibration Cutting［J］.Modern Machinery，2008（6）：44－46.

［10］刘井权，闫久春，杨士勤.超声刀切割系统的模态分析［J］.哈尔滨工业大学学报，2001，33（4）：435－438.

Liu Jingquan，Yan Jiuchun，Yang Shiqin.Modal Analysis of Ultrasonic Knife Cutting System［J］.Journal of Harbin Institute of Technology，2001，33（4）：435－438.

［11］沙金，姚志远，焦阳.超声波切割刀结构设计及切割力实验研究［C］//第十六届中国小电机技术研讨会论文集.上海，2011：201－206.

［12］孙运涛，陈超.基于近场声悬浮的非接触式直线型压电作动器［J］.中国机械工程，2010，21（24）：2951－2956.

Sun Yuntao，Chen Chao.Non－contact Linear Piezoelectric Actuator Based on Near－field Acoustic Levitation［J］.China Mechanical Engineering，2010，21（24）：2951－2956.

［13］朱华，曾劲松，赵淳生.杆式超声电机定子的动力学分析与优化设计［J］.中国机械工程，2008，19（21）：2627－2632.

Zhu Hua，Zeng Jingsong，Zhao Chunsheng.Dynamics Analysis and Optimal Design of the Stator for a Rod－shape Ultrasomic Motor［J］.China Mechanical Engineering，2008，19（21）：2627－2632.

［14］许海，赵淳生.直线型超声电机的发展及应用［J］.中国机械工程，2003，14（8）：715－717.

Xu Hai，Zhao Chunsheng.Development and Application of Linear Ultrasonic Motors［J］.China Mechanical Engineering，2003，14（8）：715－717.

［15］张铁民，刘落实，梁丽英.纵弯复合型直线超声电机振动模态有限元分析［J］.中国机械工程，2006，17（3）：251－254.

Zhang Tiemin，Liu Luoshi，Liang Liying.Finite Element Analysis on Vibration Modes for a Linear Ultrasonic Motor Using the Compound Longitudinal and Bending Vibration Modes［J］.China Mechanical Engineering，2006，17（3）：251－254.

［16］王时英，吕明，轧刚.圆锥过渡复合变幅杆动力学特性研究［J］.太原理工大学学报，2008，38（2）：95－97.

Wang Shiying，Lü Min，Ya Gang.Dynamical Research on A Cylindrical and Conical Composite Horn［J］.Journal of Taiyuan University of Technology，2008，38（2）：95－97.

［17］赵学慧，林书玉.一种新型扭转振动超声变幅杆研究［J］.陕西师范大学学报，2011，39（5）：39－42.

Zhao Xuehui，Lin Shuyu.Study on a New Type of Torsional Vibration Ultrasonic Horn［J］.Journal of Shaanxi Normal University，2011，39（5）：39－42.

［18］姚志远，杨东，赵淳生.杆结构直线超声电机的结构设计和功率流分析［J］.中国电机工程学报，2009，29（24）：56－60.

Yao Zhiyuan，Yang Dong，Zhao Chunsheng.Structure Design and Power Flow Analysis of Barstructure Linear Ultrasonic Motors［J］.Proceedings of the CSEE，2009，29（24）：56－60.

［19］赵淳生.超声电机技术与应用［M］.北京：科学出版社，2007.