The Research on Compressive Properties of Polytetraf l uoroethylene at High Strain Rate

Jun-fa ZHANG,Yu-tao JU*,Chao-xiang SUN,Peng-bo WANG

The Research on Compressive Properties of Polytetraf l uoroethylene at High Strain Rate

Jun-fa ZHANG,Yu-tao JU*,Chao-xiang SUN,Peng-bo WANG

School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China

The mechanical behaviors of polytetraf l uoroethylene(PTFE)in compressive test performed at different strain rates ranging from 10-2s-1to 103s-1are studied.The experimental results show that the yield strength increases with the increase in strain rate and exhibits a bilinear dependence on the logarithms of the stain rates,but the yield strain decreases with the increase in strain rate.Based on the mathematical model proposed by Nunes and the bilinear relationship between yield strength and strain rate,a modif i ed constitutive model which can describe its complex non-linear mechanical behavior is proposed.The experimental results are in a good agreement with the predicted results of model within 40%of strain.

CopyrightⒸ2013,China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.

Polymer materials;Polytetraf l uoroethylene;Strain rate;Constitutive model

1.Introduction

Polytetra fl uoroethylene(PTFE)is a complicated semicrystalline material.Because of PTFE physical characteristics,such as chemical stability,corrosion resistance and extremely low friction,it has been widely used not only for civil use but also for military,national defense and aerospace fi elds.Recently,there has been growing interest in the characterization of PTFE due to its complex mechanical behavior that remains one of the most severe limitations for its wider use in industries.The mechanical behavior of polymer material at low strain rate has been investigated,but its mechanical properties at high strain rate are dif fi cult to establish.The material usually needs to bear an impulse load or explosion at high strain rate.Brown et al.[1]introduced the yield action of polymer material.The research presented in this article is mainly about the mechanical properties of PTFE at different strain rates under uniaxial compression.

A universal testing machine and a Split-Hopkinson Pressure Bar(SHPB)are used to quasi-statically and dynamically test the mechanical characteristics of PTFE under uniaxial compression.The stress-strain data at the strain rates ranging from 10-2s-1to 103s-1was obtained in this study. The experimental results show that the mechanical characteristics of PTFE are obviously strain rate-dependent.A modif i ed constitutive model which can describe its complex non-linear mechanical behavior is also proposed in this paper.

2.Experiment progress

The specimens are produced by machining operation,and the height and diameter of the specimens are 3.6 mm and 10 mm,respectively.The verticality or parallelism of specimens is up to Level 7.The quasi-static test is carried out using a universal testing machine,and the stress-strain curves at the strain rates of 0.009 s-1,0.045 s-1and 0.09 s-1are obtained. SHPB technique is used to test the dynamic characteristics ofPTFE.The schematic diagram of SHPB technique is shown in Fig.1.

PTFE is a polymer material,of which strength and wave impedance are much lower than those of the metals.According to the one-dimensional stress wave theory,we need to use a super duralumin(LC4 aluminum)bar to catch the lowamplitude transmitted signals to make the transmitted signals stronger and the data more credible.The lengths of striker, incident bar and transmission bar are 300 mm,1400 mm and 1400 mm,respectively,and their diameters are 14 mm.The Young’s modulus and Poisson ratio of LC4 aluminum are 74 GPa and 0.33,respectively.Both ends of the specimen need to keep a good parallelism to decrease the lateral inertia effect and frictional effect as far as possible.During SHPB testing, we use molybdenum disulf i de as the lubricant wiped on both ends of the specimen and the surfaces of the incident and transmission bars which contact with the specimen’s ends in order to decrease the interfacial friction[2].

The impact speed in test is very high so that it is very important to keep the stress equilibrium of specimen.To achieve the stress equilibrium,the transmitted wave should be equal to the sum of incident wave and ref l ected wave[3],as shown in Fig.2.It can be seen from Fig.2 that the sum of incident wave and ref l ected wave in the experiment coincides with the transmitted wave measured directly,so the experimental result is reliable.

According to the one-dimensional stress wave theory,the train εs(t),stress σs(t)and strain rate of˙εs(t)the specimen can be calculated by two-wave method

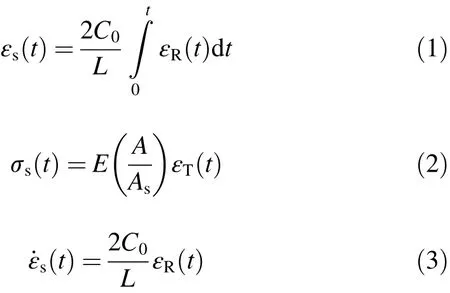
where εR(t)and εT(t)are the time-resolved ref l ected and transmitted strains in the incident and transmission bars with cross-sectional area A;E is the Young’s modulus of bar material;C0is the elastic bar wave speed in the bar material;Asand L are the cross-sectional area and the original length of specimen,respectively.

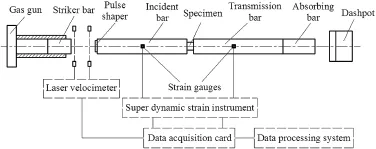
Fig.1.SHPB experimental system.

Fig.2.Stress equilibrium.

A pulse shaping technique is used to get the ideal waves.In other words,the purpose is to facilitate the stress equilibrium and constant strain rate deformation of specimen.As shown in Fig.1,a pulse shaper is put between the striker and incident bar.The most ideal pulse shaping material depends on the mechanical characteristics of the specimen and the speed of the striker.In the paper,we mainly adopt asbestos tips as the pulse shaping material.The shapes of the tips are circular,and their diameters equal that of bar.Fig.3 illustrates the comparison of waveforms with and without pulse shaper.It can be seen from the above f i gures that the waveform with pulse shaper has less high frequency oscillation than that without pulse shaper,so the inf l uence of high frequency oscillation on the experiment data can be reduced.The increase in the rising time of incident wave is benef i cial to achieve the stress equilibrium.After pulse shaping,there is a plateform on the ref l ected wave.According to Eq.(3),we can know that the strain rate is proportional to the ref l ected signal.Therefore,the ref l ected wave should be kept constant in order to achieve a constant strain rate during the deformation progress.In conclusion,Fig.3 shows that the pulse shaping technique meets the requirements above mentioned.

3.Experimental results and discussion

Fig.4 shows the compressive true stress-true strain curves of PTFE obtained at the strain rates ranging from 10-2s-1to 104s-1.It can be seen from Fig.4 that the mechanical characteristics of PTFE are strain rate-dependent and the initial modulus of dynamic increases markedly;After yielding,the material manifests strain hardening that can continue to a large strain range;The rising trend is roughly the same at different strain rates,which indicates the strain rate effect is unconspicuous in plastic section;The dynamic compressive true stress-true strain curves show the oscillations which may be due to the instability under impact loading during experimental measurement.The ends of dynamic compressive true stress-true strain curves decline.That is because the length of striker limits the width of loading pulse but not the material characteristics.

The yield stresses at the different strain rates are presented in Table 1.It can be seen from Table 2 that the yield stresses increase with the increase in strain rates,and the dynamic yield stresses are about two times of quasi-static yield stresses.

Walley and Field[4],Rae and Dattelbaum[5,6],Jennifer and Clive[7]got the stresses of PTFE at 15%of strain at room temperature,as shown in Fig.5.The result in this paper is consistent with others,which further proves the reliability of the result.

A lot of scholars do some research on the relation of yield stress-strain rate of polymer materials.Hu et al.[8]used a power-law constitutive model for the description of polycarbonate(PC)

Fig.3.Waveform f i gures of incident and transmission bars.

Fig.4.Stress-strain curves at different strain rates.

Table 1Material performance data at different strain rates.

Table 2The values of λ at different strain rates.

where A,B and m are three undetermined coeff i cients.

Richeton et al.[9]and Fu S.et al.[10]proposed the modif i ed models on the basis of Eyring theory.Mohd et al. [11]adopted the thermal activation to describe the yield stresses of polycarbonate(PC),polyethylene(PE)and polypropylene(PP).The thermal activation has the following form

Fig.5.Comparison of PTFE strengths at room temperature and 15%of strain.

where σiis the internal stress,k is Boltzmann’s constant,T is the absolute temperature,v is the activation volume,n is the material parameter,and 2kT/v is the characteristic strain rate. 2kT/v can be served as an unknown factor during numerical fi tting.

Based on the previous experimental results,Jennifer et al. have proven that the compressive yield strength of PTFE exhibits a bilinear dependence on the logarithms of the stain rates.Jenniferetal.alsoexplainedtherelationbetweentheyield stressandthestrainratebyusingadynamicmechanicalanalyzer (DMA)and the basic train rate-temperature equivalence principle.Hethoughtthatitisbecauseofphasetransitionofmaterial rather than inertia effect or stress ununiformity.The phase transition of material causes the rapid increase in compressive yield stress after a certain strain rate is achieved.

The fi tting results of experimental data obtained by the power law model and the modi fi ed thermal activation model are shown in Fig.6(a).It can be seen from Fig.6(a)that the fi tting results obtained by the two kinds of model are very close.The fi tting lines are almost horizontal at low strain rate and have a large deviation.From the experimental result,we can see that the compressive yield stress is strain ratedependent.Fig.6(b)illustrates the fi tting result from the bilinear model.Compared with the results from the power law model and the modi fi ed thermal activation model,the results from the bilinear model are in better accord with the experimental data.The fi tting result in this paper and the other experimental data further prove the reliability of the bilinear model provided by Jennifer[7].

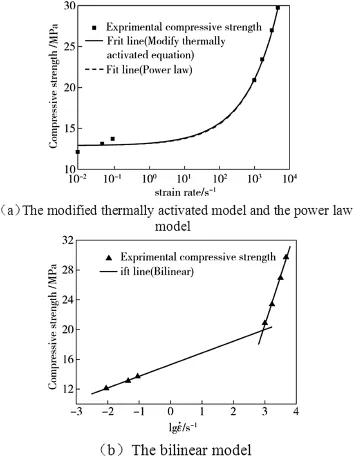
Fig.6.Compressive strengths at different strain rates.

4.Constitutive model of PTFE

A mechanical model proposed by Nunes[12]is used for studying the tensile mechanical behavior of PTFE at low strain rate.It can be expressed as

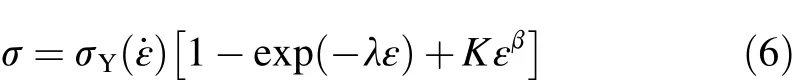
where K is the strengthening factor,β is the strain-hardening index,and λ is def i ned as a material constant.

The comparison of the experimental data and the f i tting result by Nunes’model is shown in Fig.7.The model f i ts well after yielding but has a large error for viscoelastic part.There are different initial moduli for general composite material at different strain rates,but the Nunes’model could describe the behavior.

The strengthening factor K and the strain-hardening index β in Eq.(6)are related to the increase in stress-strain,but are not related to the strain rate.So K and β are the same at different strain rates.The material constant λ has an inf l uence on the initial modulus.So in this paper,λ is def i ned as a strain rate-dependent item and has a power law relationship with the strain rate.The modif i ed model is def i ned as

The compressive stress-strain behaviors of PTFE at the strain rates of 0.009 s-1,0.09 s-1,1000 s-1and 3150 s-1are used to determine the parameters in the constitutive model. Firstly,based on the yield stresses at four different strain rates in Table 1,we can get the relationship between the yield stress σYand the logarithms of the stain rate log˙ε.The form of bilinear model is

Fig.7.True stress-true strain curves obtained by experiment and original models at different strain rates.

From the stress-strain curve of 1000 s-1,the values of K and β can be calculated by using the least square method: K=4.04,β=1.56.If K and β are put into other three strain rate curves,we can get the values of λ which is listed in Table 2.

The parameters in Eq.(7b)can be obtained by f i tting the results in Table 2.

Eqs.(8)and(9)are the strain rate-dependent constitutive equations.

The comparison between the four f i tting curves and the experimental data is shown in Fig.8.Fig.8 demonstrates a favorable agreement between the f i tting result and test data. Eqs.(8)and(9)are used to predict the stresses at 0.045 s-1, 1680 s-1and 4700 s-1,as shown in Fig.9.The modif i ed strain rate-dependent model demonstrates a favorable agreement between the predicted and test results,indicating the ability of the model to describe the mechanical behavior of PTFE in a large range of strain rates within 40%of the strain.Furthermore,the results from the modif i ed model agree with the test data in viscoelastic region.

In conclusion,the structure of the modif i ed model is very simple,and every parameter has its own physical signif i cance. The f i tting progress is very convenient,which just needs two high strain rate curves and two low strain rate curves.The modif i ed model shows a good agreement with experimental result over the range from 10-2s-1to 103s-1within 40%of the strain.

5.Conclusions

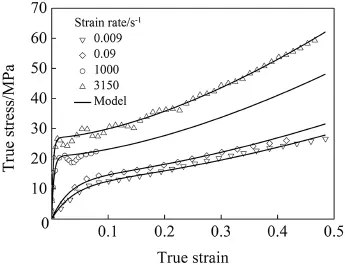
Fig.8.The f i tting curves vs the experimental curves.

The mechanical behaviors of PTFE at the different strain rates ranging from 10-2s-1to 103s-1in compressive tests were studied in this paper.The experimental results show that the mechanical behavior of PTFE is strain rate-dependent,and the yield strength increases with the increase in strain rate.The PTFE exhibits a bilinear dependence on the logarithms of the stain rates.

Based on the model proposed by Nunes and the bilinear relationship between yield strength and strain rate,a modif i ed constitutive model describing PTFE complex non-linear mechanical behavior was proposed in this paper.The experimental results are in a good agreement with the predicted results of model within 40%of the strain in a large range of strain rates.

Fig.9.The forecast curves vs the experimental curves.

[1]Rae PJ,Cady CM,Vecchio KS,et al.Inf l uence of molecular conformation on the constitutive response of polyethylene:a comparison of HDPE,UHMWPE and PEX.Exp Mech 2007;47(3):381-93.

[2]Wang XY,Lu FY,Lin YL.Study on interfacial friction effect in the SHPB tests.Explos Shock Waves 2006;26(2):134-9[in Chinese].

[3]Li WM,Xu JY,Shen LJ,Li Q.Study on 100-mm-diameter SHPB experimental techniques of dynamic stress equilibrium and nearly constant strain rate loading.J Vib Shock 2008;27(2):129-32[in Chinese].

[4]Walley SM,Field JE.Strain rate sensitivity of polymers in compression from low to high rates.DYMAT J 1994;1(3):211-27.

[5]Rae PJ,Dattelbaum DM.The properties of poly(tetraf l uoroethylene) (PTFE)in compression.Polymer 2004;45(22):7615-25.

[6]Rae PJ,Brown EN.The properties of poly(tetraf l uoroethylene)(PTFE)in tension.Polymer 2005;46(19):8128-40.

[7]Jennifer LJ,Clive RS,Jason RF,Eric NB.Compressive properties of extruded polytetraf l uoroethylene.Polymer 2007;48(14):4184-95.

[8]Hu WJ,Zhang FJ,Chang TJ,Liu ZF.Dynamic stress-strain response and yield behavior of polycarbonate.Chin J Mater Res 2007;21(4):439-43 [in Chinese].

[9]Richeton J,Ahzi S,Vecchio KS,Jiang F,Adharapurapu RR.Inf l uence of temperature and strain rate on the mechanical behavior of three amorphous polymers:characterization and modeling of the compressive yield stress.Int J Solids Struct 2006;43(7-8):2318-35.

[10]Fu S,Wang Y.Tension testing of polycarbonate at high strain rates. Polym Test 2009;28(7):724-9.

[11]Mohd FO,Akil HM,Ahmad ZA.Measurement and prediction of compressive properties of polymers at high strain rate loading.Mater Des 2011;32(8-9):4207-15.

[12]Nunes LCS,Dias FWR,Mattos HS.Mechanical behavior of polytetraf l uoroethylene in tensile loading under different strain rates.Polym Test 2011;30(7):791-6.

7 February 2013;revised 7 June 2013;accepted 4 July 2013 Available online 5 October 2013

*Corresponding author.

E-mail address:yutaoj@126.com(Y.T.JU).

Peer review under responsibility of China Ordnance Society

Production and hosting by Elsevier

2214-9147/$-see front matter CopyrightⒸ2013,China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.

http://dx.doi.org/10.1016/j.dt.2013.09.020