基于阶比复杂度的滚动轴承早期故障诊断

黄炯龙，吕建新，马文龙，曹红燕

(1.武警工程大学，西安 710086；2.广西师范大学，广西 桂林 541004)

滚动轴承作为各种工程机械设备中的关键组成部件，其工作状况对整个机组的正常运行有着重要的影响。轴承的故障诊断主要包括2个步骤:(1)从原始的轴承振动信号中提取某些特征；(2)利用人工智能方法对所提取的特征进行判断，以确定轴承是否存在故障[1]。

上述针对轴承早期的故障诊断主要是对振动信号的波形参数进行特征提取，虽然具有一定的效果，但仍然存在以下不足：(1)与正常波形相比，轴承早期故障振动变化信息不明显,简单地通过波形参数并不能完全将轴承的早期故障信息表示出来；(2)不同状态下的轴承故障信号由于能量量级差别明显，可比性比较差；(3)噪声对波形参数影响较为明显，从而影响故障信息识别；(4)目前所使用的人工智能方法都需要故障样本进行诊断，但轴承的早期故障样本特征并不明显，影响诊断的准确性和快速性。

轴承的早期故障信息往往会使该系统的动力学参数产生较为明显的变化，因此，复杂度作为非线性时间序列分析中一个重要指标，对系统的状态变化很敏感，可以作为轴承早期故障诊断的依据。由于轴的转速不是恒定的，转速上的波动会影响轴承振动信号的随机性，从而影响复杂度的计算。阶比跟踪技术是针对转频不稳定机械的一种专用振动测量技术，它通过对轴转速进行跟踪实现恒角度增量采样[2]，可将机械变速过程中产生的与转速有关的振动信号有效地分离出来，同时对与转速无关的信号起到一定的抑制作用[3]。由于阶比跟踪按转角位置重新分配信号的采样间隔，所以剔除了转速变化对信号随机性的影响。

1 复杂度

文献[4]将复杂度定义为产生某给定“0，1”序列所必需的最少的计算机程序的比特数。文献[5]在上述定义下提出了一种基于系统内在结构或过程的量度符号序列复杂性的简单算法，即L-Z复杂度。

(1)已知重构序列{x1,x2,…,xn}，令

(1)

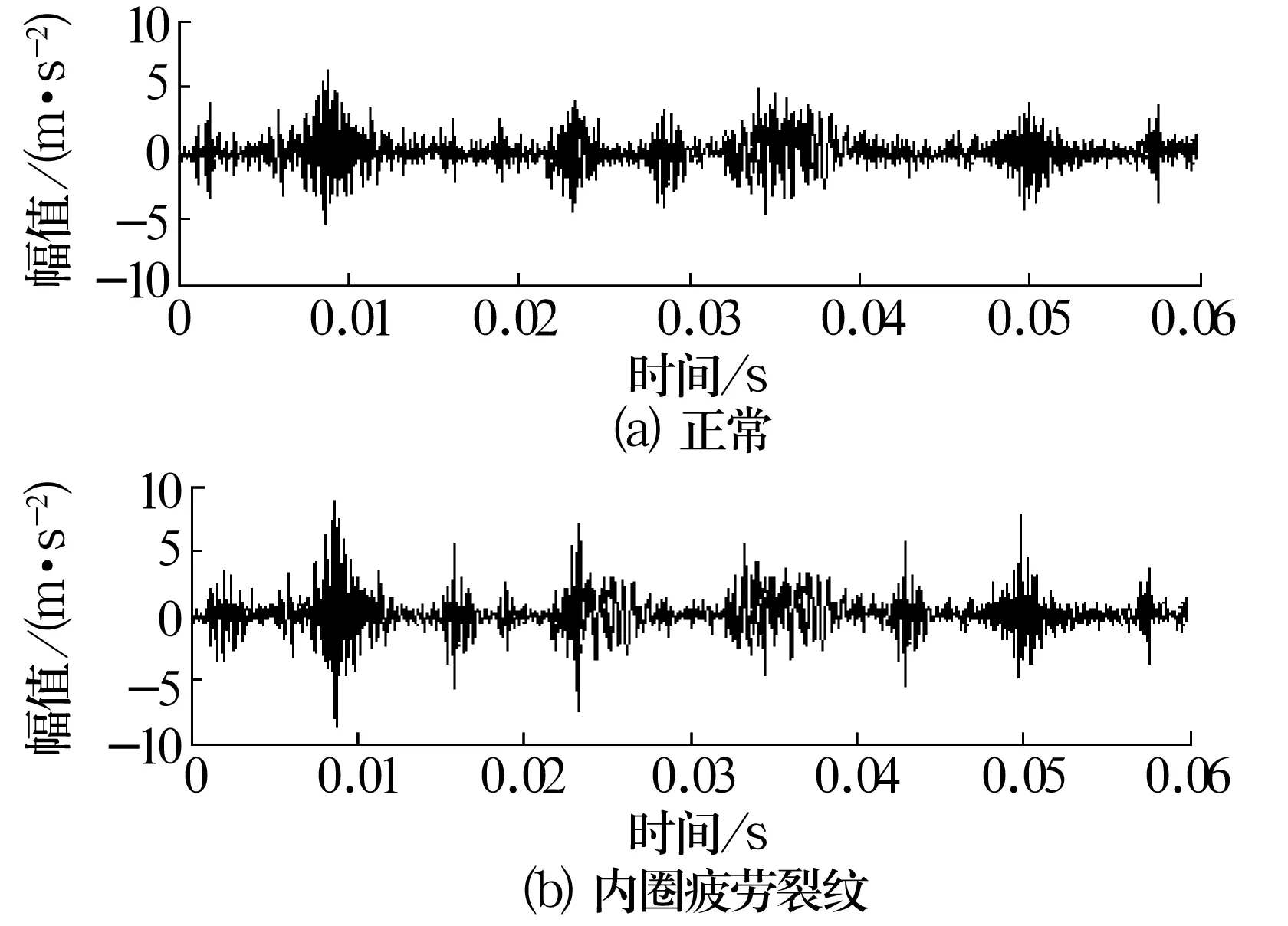
(2)根据(1)式将{x1,x2,…,xn}映射为新的序列{s1,s2,…,sn}，令Q=sr+1，r

(3)将“•”前的所有字符看作S，重复上述步骤直至生成整个序列。

(4)根据上述步骤得到一个用“•”分段的字符串，该字符串被“•”分成段的数目即为该序列的复杂度C(n)。

(5)据文献[5]的研究，几乎所有0，1随机序列的复杂度都趋于值B(n)，即

(2)

通过归一化，可得相对复杂度

R(n)=C(n)/B(n)。

(3)

由上述算法可知，复杂度反映了随序列长度增长而产生新模式的速度，相对复杂度R(n)反映一个序列与随机序列的接近程度，即序列复杂度越大，说明数据在某一时期内的新变化越多，发生新变化的速率越快，表明数据变化是无序而复杂的。反之，如果复杂度越小，则说明该序列发生新变化的速率越慢，周期性越强，数据变化是规律的。当信号完全为随机信号时，R(n)=1；当信号为周期信号时，R(n)=0。

综上所述，复杂度能够描述序列发生变化的情况，可以作为振动信号所代表的轴承系统状态的非线性特征参数。

2 基于阶比复杂度的轴承故障诊断

由于轴承周围噪声信号的相对复杂度接近1，会直接影响轴承振动信号的复杂度，对故障特征提取不利。故选用小波阈值法先对信号降噪以减小噪声信号的影响。

基于阶比复杂度的轴承故障诊断具体包括以下步骤：

(1)选取db4小波对信号进行小波阈值降噪；

(2)根据文献[6]，轴承的参考轴在短时间内可看作是匀变速运动，因此，参考轴转角-时间函数可用多项式表示为

θ(t)=b0+b1t+b2t2+···+bntn，

(4)

式中：bn为待定系数，可以通过角域重采样后的数据获得；t为时间点。

在时域信号中，转过相等角度Δα的连续时间为ti，可得

(5)

将(5)式代入(4)式，可求得待定系数bn，为简化计算取n=3得

(6)

(7)

将t0，t1，t2和对应的参考轴转角代入(4)式可得

(8)

由此可以得出关于等角度采样点的方程，在求出信号对应的时间点后通过插值算法即可实现时域信号的计算阶比跟踪重采样，得到等角度分布的采样点χ(m)；

(3)按前面所述步骤计算角域信号χ(m)的相对复杂度Ri(n)，通过不同的相对复杂度Ri(n)判别轴承的早期故障。

3 试验与分析

在某型齿轮箱振动试验台上进行试验验证，试验系统中由电动机带动输入轴,输出轴带动负载，主动齿轮齿数Z1=35，被动齿轮齿数Z2=50。轴承疲劳裂纹是轴承早期故障的主要形式，因此试验选取正常和模拟内、外圈疲劳裂纹的6206Z轴承样本进行分析。轴承内径30 mm，外径62 mm，宽度16 mm，极限转速为11 000 r/min，分别在内、外圈上通过线切割制作深1 mm，宽1 mm的沟槽模拟轴承早期疲劳裂纹故障。

鉴于加速阶段的振动信号与恒转速时相比往往含有更多的轴承故障信息，为了能在信号中进一步突出轴承的早期故障，在轴转速由静止加速至1 500 r/min的过程中对轴承信号进行等时间的同步采样，采样频率为12 kHz，采样时间为2 s。

无故障状态和模拟内圈疲劳裂纹的轴承振动信号时域波形如图1所示，从图中可以看出，正常状态与早期故障轴承时域波形没有明显差别。

图1 轴承时域信号

为了进一步对比传统阶比分析与阶比复杂度的故障识别效果，首先，采用传统阶比分析方法，在对时域信号进行角域重采样后进行FFT分析，结果如图2所示。从阶比图中可以看出，轴承的早期故障无法得到有效的识别。然后，采用阶比复杂度对10组经过角域重采样后的信号进行分析，计算所得复杂度见表1。

图2 轴承阶比谱

根据相关数据分析，该型号轴承正常工况下复杂度一般为0.3～0.4，复杂度大于0.5即可认为该轴承可能出现了早期故障。从表中可以看出，轴承内、外圈疲劳裂纹信号的复杂度明显大于正常状态下的轴承振动信号，说明轴承早期故障会使振动信号表现出更强的随机性。受振动信号传递路径的影响，轴承的内、外圈裂纹也表现出不同的复杂性测度，且外圈裂纹对应信号的复杂度大于内圈。由此可以根据轴承信号的相对复杂度来判别轴承的早期疲劳裂纹故障。

表1 轴承振动信号相对复杂度对比

4 结束语

通过小波降噪和计算阶比跟踪不仅有效消除了转速的波动对轴承振动信号复杂度计算的影响，还将时变时域信号转变为准平稳角域信号，提高了复杂度计算的准确度。试验结果表明：轴承的早期裂纹故障信息在时域和阶比谱上不够明显，但与正常轴承相比，出现早期疲劳裂纹故障后，轴承振动信号的复杂度则会明显增大。由此表明，与传统的特征频率分析相比，阶比复杂度在表征轴承早期故障信息方面具有很强的能力，可作为轴承状态监测和早期故障诊断的一种无量纲指标，无需经过其他复杂的模式识别方法即可实现轴承的早期故障诊断，与使用人工智能算法相比速度明显提高。