滚动轴承最佳工作游隙的确定及分析

白雪峰，郭长建，赵联春

(1.人本集团 a.C&U Americas,LLC，MI 48170;b.技术中心，上海 201411；2.上海斐赛轴承科技有限公司，上海 201100)

游隙对滚动轴承的综合性能具有十分重要的影响。在安装和运行条件一定时，游隙大小决定着轴承的载荷分布和最大接触应力，并决定着轴承的疲劳寿命。因此存在最佳工作游隙，使得轴承的疲劳寿命最长，研究轴承的最佳工作游隙及其影响因素具有重要的工程意义。

1 游隙的定义及影响因素

轴承游隙指轴承在未安装于轴或壳体上时，将其内圈或外圈中的一个固定，然后使未被固定的一方做径向或轴向移动时的移动量。根据移动方向，可以分为径向游隙和轴向游隙。此处即所谓的原始游隙，也就是设计时的理论游隙G0。

理论游隙减去轴承安装在轴或壳体上时套圈因过盈配合产生的膨胀量或收缩量后的游隙称为安装游隙或残留游隙Gf。因过盈配合导致套圈膨胀或收缩的游隙变化量用δf表示，对于内圈则使用δΔs表示，对于外圈则使用δΔh表示，δf=δΔs+δΔh。

安装游隙减去轴承工作温度及其内部各零件温差引起的游隙变化量后的值称为有效游隙Gt,其中各零件温差引起的游隙变化量用δt表示。

轴承安装在机械上承受一定载荷旋转时的内部游隙，即有效游隙加上轴承载荷产生的弹性变形量后的游隙，称为工作游隙Gr。轴承游隙的影响因素如图1所示。

2 最佳工作游隙的确定

2.1 工作游隙与载荷分布之间的关系

根据轴承运行工况特点，应有针对性地选择载荷分布系数，而工作游隙与载荷分布系数之间存在关联，因此，有必要讨论两者之间的关系。

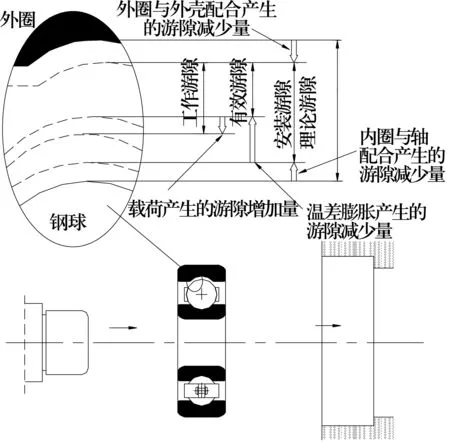
图1 轴承游隙的影响因素

轴承的额定载荷实际上随着游隙的变化而变化[1]。对于向心轴承，假定内、外圈只有径向位移，其额定动载荷的计算是在轴承的工作游隙为0(载荷分布系数ε=0.5)的前提下进行的。

假如轴承寿命取决于旋转套圈，当工作游隙为0时的寿命为L，工作游隙不为零时的寿命为Lε[2]，则

(1)

式中：Jr为径向积分；J1为与旋转内圈的平均滚动体载荷有关的积分(表1)[3]；Jr(0.5)和J1(0.5)分别为ε=0.5时的Jr和J1；p为寿命指数，球轴承p=3,滚子轴承p=10/3。使用Matlab的积分函数quad进行编程，计算了J1和J2(J2为与静止套圈的平均滚动体载荷有关的积分)。结果发现文献[3]中滚子轴承的J1和J2与精确计算结果有出入，而球轴承完全一致，在此为了应用方便也给出了修正值，供参考使用(表1)。

工作游隙Gr和载荷分布系数ε的函数关系如下，对于深沟球轴承

(2)

对于圆柱滚子轴承

(3)

式中：Fr为径向载荷，N；Z为滚动体数目；Dw为滚动体直径，mm；Lwe为滚子的有效长度，mm。

对于不同载荷分布下轴承的修正寿命与额定寿命的比值可以通过(1)式求得。不同的载荷分布系数ε对应的f(ε)和Lε/L见表2，由此根据(2)～(3)式可求得不同游隙下的载荷分布系数和寿命比Lε/L。计算可知，当ε=0.7～0.8时，轴承能够获得最长的疲劳寿命，约为L10的1.1倍。此时，轴承最大寿命对应的游隙应该为负游隙。

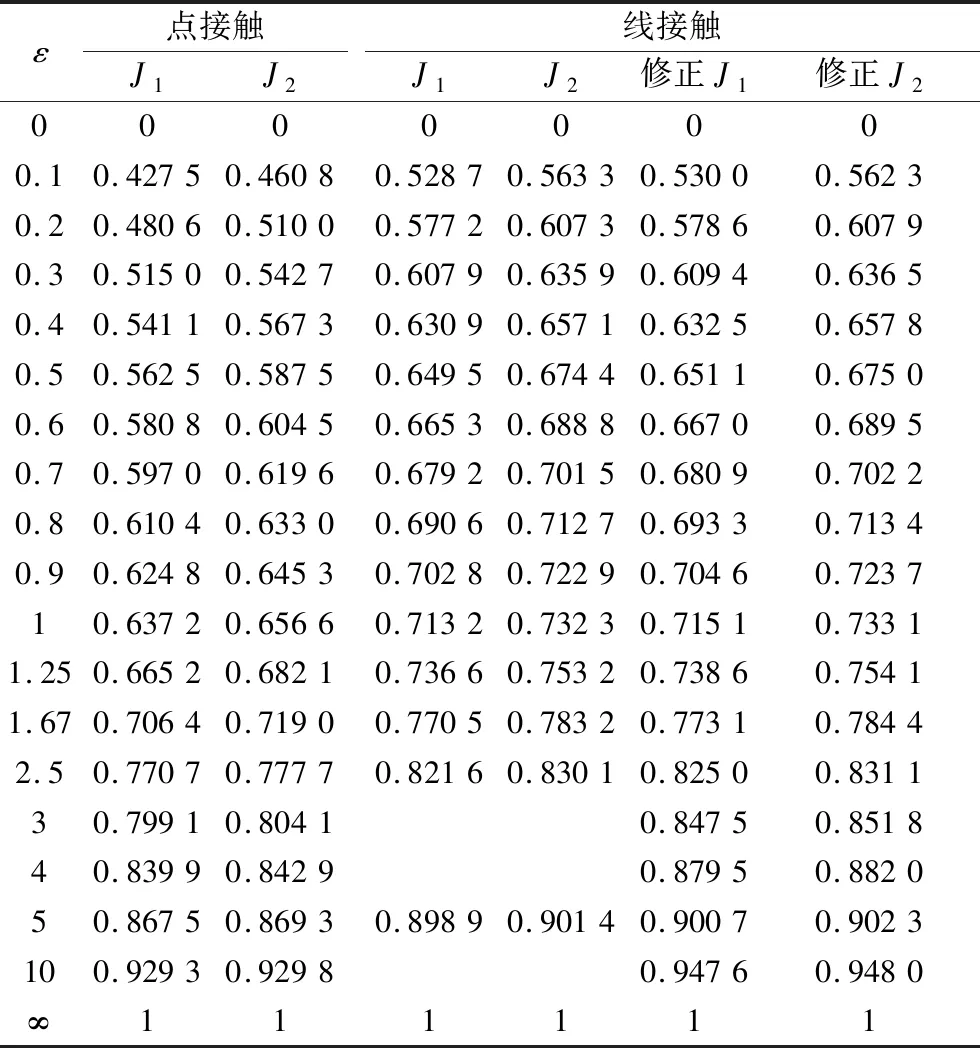
表1 单列轴承与旋转内圈的平均滚动体载荷有关的积分

表2 不同载荷分布的寿命比

2.2 最佳工作游隙的确定

轴承疲劳寿命受材料特性、热处理、润滑条件、工作温度、载荷条件、几何尺寸和内部游隙等许多因素的影响。其中，游隙对轴承疲劳寿命的影响显著。6310轴承的寿命与其工作游隙的关系如图2所示。由图2可知：轴承有一个小的负游隙时可以获得最长疲劳寿命，当游隙偏离此值时其寿命开始下降，尤其在负方向下降较快。因此，为了获得最长的疲劳寿命，必须在最大点处分配工作游隙公差，从而保证轴承寿命在一个特定值附近变化。由于实现最长疲劳寿命对应的工作游隙值较难控制，通常将工作游隙设定在最大疲劳寿命对应工作游隙值的正侧。实际选取时，可以保守地将工作游隙设为零或微负值。

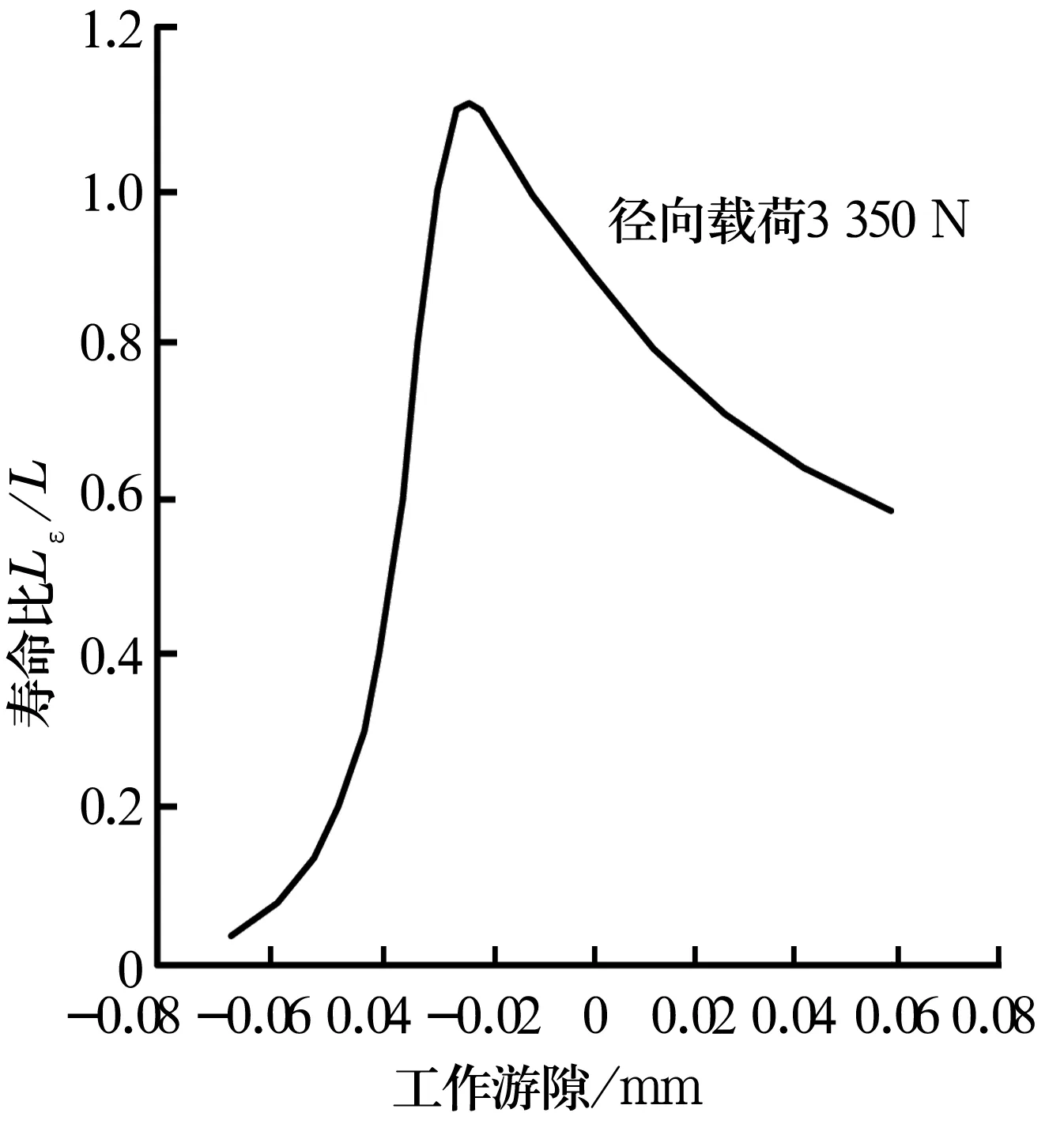
图2 6310轴承工作游隙与疲劳寿命的关系

然而由于装配过程中分配的游隙公差受很多因素影响，且安装游隙难于测量，因此要保证轴承在工作时有一个与疲劳寿命对应的特定游隙值，必须分析影响游隙的各种因素，并认真计算。

由于轴承及其配合部件的尺寸符合正态分布，如果没有从概率统计的角度出发，得到的计算结果往往与实际情况不符。基于此计算结果选配轴承游隙时，在安装和运转工况下轴承处于最佳工作游隙的概率较低。

3 游隙影响因素分析

3.1 公差模型

通常，制造组件的尺寸可以按统计学理论进行分配，如图3所示。如果99.7%组件的尺寸A的分配公差为±ΔA，那么平均尺寸为A，标准方差为

σ=ΔA/3 。

(4)

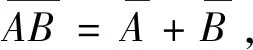
(5)

(6)

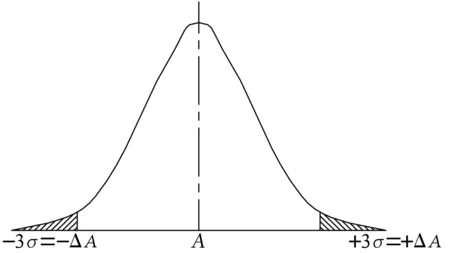
图3 尺寸的正态分布

3.2 配合对游隙的影响

轴承的配合选择通常根据套圈相对于载荷方向的运转状态而定[6]。当套圈相对于载荷方向固定时，一般选择平均间隙较小的过渡配合或极小的间隙配合。当套圈相对于载荷方向旋转时，一般选择过盈量较小的过盈配合或过盈概率大的过渡配合。作为过盈配合计算的基础，一般假定套圈、轴、轴承座都是厚壁圆环[7]，相互以过盈配合安装在一起。

在用压力法安装轴承时，由于配合表面粗糙度的影响会产生表面压平现象，在计算过盈配合时应对此进行适当的考虑[7]。

对于磨削轴

(7)

对于车削轴

(8)

对于磨削座孔

(9)

对于车削座孔

(10)

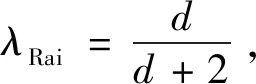
由轴和轴承配合引起的平均名义过盈量Δda为

Δda=ds-di，

(11)

过盈量的标准偏差为

(12)

式中：ds为轴径的平均值；di为轴承内径的平均值；σs和σi分别为轴径和轴承内径的标准偏差。

则内圈与轴配合引起的游隙减小量为

(13)

将表面粗糙度引起的过盈变化率λRai引入(13)式得

δΔs=λiλRaiΔda。

(14)

相似的，由座孔和轴承的配合引起的平均名义过盈量、平均径向游隙减小量、标准偏差分别为

ΔDa=De-Dh，

(15)

(16)

(17)

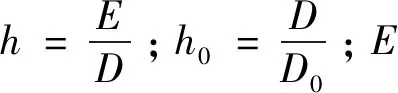
则安装游隙的平均值和标准偏差为

GΔf=GΔ0-δΔs-δΔh，

(18)

(19)

式中：GΔ0和σΔ0分别为原始径向游隙的平均值和标准偏差。考虑到轴承内径、外径、轴及座孔的尺寸以及原始游隙均为正态分布，这里采用6σ进行分析，可以包含99.7%的情况，仅有0.3%的概率超出这个分析范围。

3.3 温度及材料的影响

工作温度对轴承径向工作游隙的影响表现在2个方面：(1)温度引起轴承内、外圈配合的有效过盈量的变化，由此间接影响工作游隙；(2)外圈、内圈与钢球间温度的差异造成各零件热膨胀不一样，进而影响工作游隙。

3.3.1 内、外圈温差造成的游隙变化

由于钢球的温度难以测量和判断，因此假设钢球的温度等于内圈的温度，则内、外圈温差引起的游隙减小量为

δt=αΔTE，

(20)

式中：δt为内、外圈温差引起的游隙减小量,mm; ΔT为内、外圈的温差，℃(一般情况下内、外圈温差为5～10 ℃，在轴承有相对气流冷却时为15～20 ℃[8])；α为轴承钢的线膨胀系数，α=12.5×10-6℃-1。

3.3.2 不同材料线膨胀率造成的游隙变化

为了减轻重量，降低成本，提高主机的工作性能，轴承座常常采用较轻的铝合金等材料。此时，工作中轴承的温升将会使配合面的有效过盈量发生变化，进而影响轴承的有效工作游隙。

当轴承座和套圈材料不同时，工作中温升导致的外圈配合面的过盈量变动量为

ΔDT=(α2ΔT2-α1ΔT1)D，

(21)

式中：α1和α2分别为座孔、套圈的线膨胀系数；ΔT1为靠近配合面的座孔温升, ΔT2为靠近配合面的外圈温升。一般来说，座孔的温升与外圈的温升存在较小的差异，为了计算方便假设两者温升相同。则

ΔDT=(α2-α1)ΔT2D。

(22)

进一步假设内圈配合面的温升ΔT3与外圈配合面的温升相同，即ΔT2=ΔT3。同理，工作中的温升导致的内圈配合面的过盈量变动量为

ΔdT=(α3-α2)ΔT3d，

(23)

式中：α3为轴的线膨胀系数。

这里推导了具有不同线膨胀系数的轴与内圈或外圈与座孔在温升的影响下配合过盈量的变化。那么轴承工作中由于温升发生膨胀造成的自身的游隙增加量为

δΔT=λeΔDT+λiΔdT。

(24)

在考虑轴承的整个生命周期时，轴承的实际工作温度其实是一个很宽的范围，通常低温为-40 ℃，高温则要根据实际情况而定。因此计算游隙时必须考虑整个温度范围，而不能只考虑内、外圈的温度差。

3.4 工作载荷和离心效应引起的游隙变化

文献[8]从轴承的载荷分布阐述了工作载荷对游隙的影响。其认为不应该在研究径向游隙时把工作载荷引起的弹性变形量作为工作游隙的增量。因此，在一般的工况计算里可以不考虑工作载荷的影响，因为在轴承实际工作时，工作载荷引起的弹性变形量可以使工作游隙变大，即使将游隙取为微负值也会相对保险。

同时，对于转速相对不高的轴承，离心效应引起的游隙变化可以不予考虑。

总之，轴承工作游隙的确定非常复杂，除了上述因素的影响外，还有其他因素，如大的轴向载荷或力矩、套圈热处理的尺寸稳定性、轴承的磨损和工作状态等，这些因素可以在特定的工作条件下予以考虑。

轴承的工作游隙可以表示为

Gr=G0-δf-δt-δΔT。

(25)

需要注意的是，在利用(25)式进行计算时，需对安装配合引起的游隙变化量进行6σ分析，见(18)～(19)式。因此，可以基于(25)式及理论设计的最佳工作游隙，反算出轴承的最佳原始游隙。

4 实例计算和分析

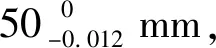
4.1 轴承安装游隙的计算

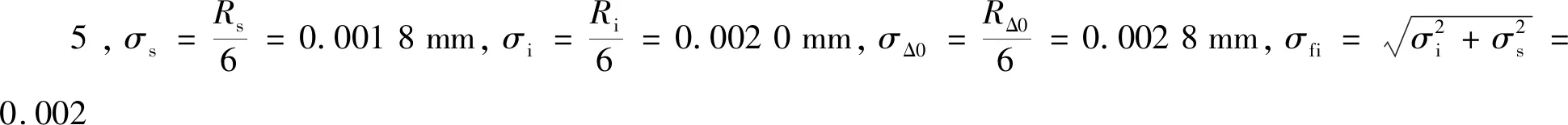
则由(18)～(19)式得

GΔf=GΔ0-δΔs-δΔh=GΔ0-λiλRai(ds-di)-0=

0.004 2 mm，

则安装游隙值范围为

Gf=GΔf±3σΔf=-0.006 3～0.014 7 mm。

4.2 温升及内、外圈温差对游隙的影响

假定内、外圈的温差为5 ℃，则

δt=αΔtE=0.006 3 mm。

假设轴承工作温度为100 ℃，则内圈配合面的温升ΔT3=80 ℃，则由(23)式得

ΔdT=-0.004 8 mm；

由于外圈和座孔为间隙配合，所以ΔDT=0。

那么由(24)式得

δΔT=0+λiΔdT=-0.003 8 mm。

则由(25)式得，轴承在100 ℃下工作时的工作游隙分布为-0.008 8～0.012 2 mm。由这个实例计算可以看到，轴承的工作游隙平均值为0.001 7 mm，同时考虑工作游隙的范围，以上结果可以保证轴承工作游隙在最佳游隙值正侧分配。

5 结论

(1)在轴承尺寸、材料、安装及运转条件确定的情况下，最佳工作游隙与载荷分布系数相关。

(2)以最佳工作游隙为参照点，游隙增大或减小时，轴承寿命均下降，在该游隙值的负侧，寿命急剧下降，而在该游隙值的正侧，寿命下降相对较慢；因此，轴承工作游隙范围应根据轴承寿命的要求，选择最佳工作游隙值正侧的区域。

(3)对J1的计算结果进行了修正，给出了根据温度范围计算游隙的方法。

(4)采用6σ原则，基于(25)式及理论确定的最佳工作游隙范围，可以反算出轴承的最佳原始游隙范围，基于此范围选配轴承，可以保证轴承工作时处于最佳工作游隙，从而具有较长的疲劳寿命。

(5)结合轴承载荷分布与疲劳寿命的关系对轴承的各种游隙进行了计算，为轴承的预紧力计算及最佳预紧力的确定提供了重要思路。文中的计算方法适用于所有类型的向心轴承。