时空混沌二值化方法研究

李红燕，杨万利

装甲兵工程学院基础部，北京 100072

时空混沌二值化方法研究

李红燕，杨万利

装甲兵工程学院基础部，北京 100072

1 引言

密码学中序列密码的安全性依赖于伪随机序列的随机性和不可预测性。由于混沌系统可以提供具有良好随机性能的伪随机序列，因此在密码学中具有很大的应用价值。将混沌实值序列直接应用于加密系统是不安全的[1]，也不实用，所以更多的应用是由混沌序列生成的二值序列。在扩频通信系统中，抗干扰、抗噪声、抗截获、信息数据隐蔽和保密、多径保护、抗衰落、实现同步与捕捉等都与扩频序列的随机性能密切相关，所以扩频序列的随机性能的好坏是很重要的。实值序列二值化的问题是混沌应用的第一步，该过程将直接影响后续序列的随机性、复杂性，最终影响系统的安全性。因此有必要对产生混沌二值伪随机序列的算法进行研究，使得生成的伪随机序列满足各种安全需求，避免系统遭到攻击。

由混沌系统产生随机序列，首先要选择混沌系统。采用低维混沌系统，一方面有被攻破的危险[2]，另一方面，利用现有的量化方法得到的二值序列都不能满足随机性要求[3]。于是人们开始尝试使用超混沌系统[4-5]、带时延的混沌系统[6]或时空混沌系统[7-11]来产生混沌序列。

最主要的混沌二值伪随机序列的产生方法是符号函数二值化法。近年来，也有相关文献采用新的方法如比较法、区间法等来生成混沌二值伪随机序列[7，12]，但是它们在原理上都类似，有的则是多种方法的组合。例如，文献[13]使用了一种二值化方法，将序列归一化后转换成二进制形式，但文献[14]证明该方法与区间法是等价的。而且每一种方法都是针对一类特出的混沌系统提出的。事实上，目前没有公认的提取方法对所有的混沌序列有效，所以有必要针对混沌系统的特点研究二值序列的提取方法。

本文基于耦合映像格子模型，研究时空混沌序列的二值化方法。研究显示采用耦合映像格子模型产生的时空混沌序列由符号函数二值化法得到的混沌二值伪随机序列的性能也有缺陷[12]。文献[12]中给出了一种改进的符号函数二值化的方法。将一个格点的值取反，加上另外一个格点的值，但是该方法并不能适合所有类型的耦合映像格子模型。本文在符号函数二值化法的基础上，给出了一种新的二值化方法——基于符号函数二值化法的阈值调整技术和序列抽取技术相结合的二值化方法，采用严格的NISΤ（美国国家标准与技术委员会）测试标准[15]对得到的二值伪随机序列进行了测试，通过大量的测试和分析说明得到的序列性能良好。

2 混沌序列的生成

最常用的生成时空混沌序列的系统为单向耦合映像格子（One-way Coupled Map Lattice，OCML）：

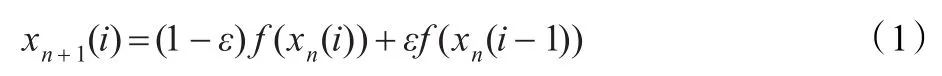
其中f(x)=4x(1-x)，x∈(0，1)，n表示离散化后的时间，i表示格子空间坐标。ε为耦合强度，当0.75〈ε〈1时，具有相同驱动序列的两个不同的耦合映像格子系统能够达到同步，这一点对于将时空混沌应用于保密通信系统很重要。

在生成时空混沌序列时除了给定初始时刻所有格点处的值，还要给定第一个格子处的值，也就是驱动序列。驱动序列的选取很重要，它能影响同步性能和产生的时空混沌序列的性能，不影响研究，在本文中数值模拟时驱动序列和初值都用MAΤLAB自动生成的随机序列。

ε=0.8时，系统式（1）的演化图（3 000步）如图1所示。

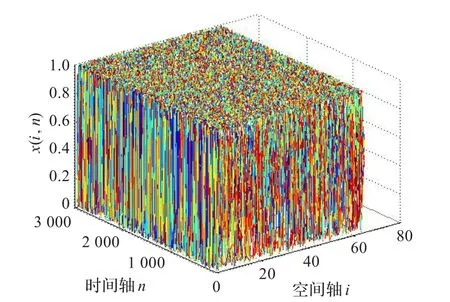
图1 系统式（1）的时空演化图

本文中用a(i)(n)，n=1，2，…，N表示一次实验得到的第i个格子处产生的时空混沌序列，a(10)，即第10个格子处的时间发展行为如图2所示。

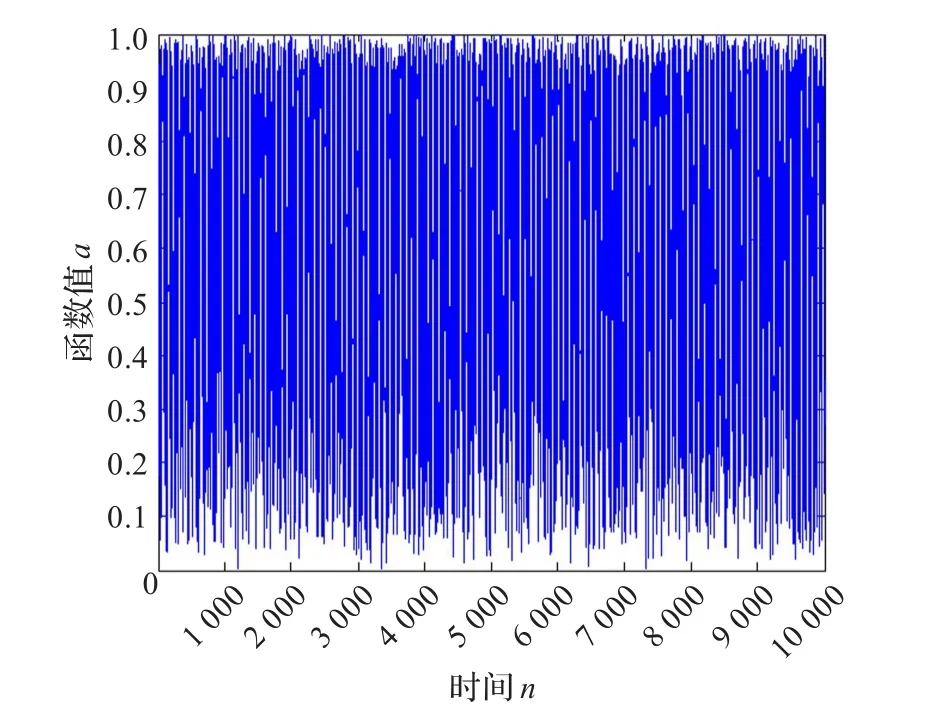
图2 a(10)的时间发展行为

3 伪随机序列的检测方法

如果一个序列，一方面它是可以预先确定的，并且是可以重复地生产和复制的；一方面它又具有某种随机序列的随机特性（即统计特性），便称这种序列为伪随机序列。

伪随机序列是具有某种随机特性的确定的序列。其随机性只能通过统计测试去验证。检验序列是否是伪随机序列，主要是通过统计测试检验序列是否具有一些随机序列具有的随机特性。伪随机序列的统计测试方法有很多，但是需要说明的是，通过所有的测试都不能说明一个伪随机序列是真随机的，只是说明序列的随机性能比较好，如果不能通过某个测试，则说明序列的随机性能不好。下面介绍几个主要的二值随机序列随机性能优劣的检验方法。这些方法来自美国商务部国家标准技术协会（NISΤ）于2001年5月公布的FIPS140-2。标准包括16项统计测试，但对时空混沌来讲，最主要的测试包括频率测试、游程测试、谱测试和相关性测试[14]。

（1）频率测试：频率测试的目的是检验这个序列中0和1的比例是否近似相等。具体的测试方法如下：

步骤1将0，1组成的序列转换成由-1，1组成的序列，设序列的长度为n，转换方法为xi=2εi-1，i=1，2，…，n。其中，εi，xi为转化前后的比特值。计算转化后的序列和Sn，即

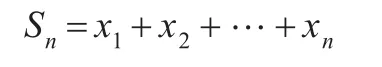
步骤2计算统计值Sobs，即

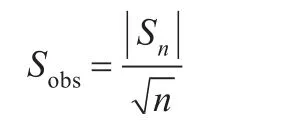
步骤3计算判断标准P-Value的值：

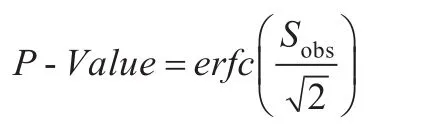
其中，erfc()为互补误差函数，即

若P-Value的值小于0.01，则认为测试的系列不是随机序列；反之，则认为序列是随机序列。

（2）游程测试：游程是指连续的0或1的不同长度的子序列，游程测试的目的是计算序列中游程的个数，并判断0 和1的游程个数是否与随机序列一致。具体测试方法如下：

步骤1对需要检测的序列进行预处理，计算1在序列中的比例，即

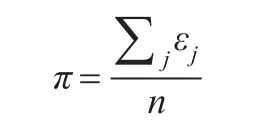
其中，n为序列长度，εj为比特值。

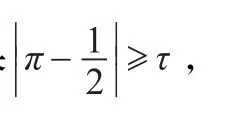
步骤3计算统计值：

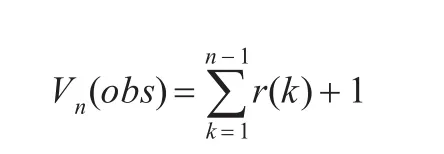
其中，r(k)的取值为：若εk=εk+1，则r(k)=1；反之r(k)=0。

步骤4计算判断标准P-Value的值：

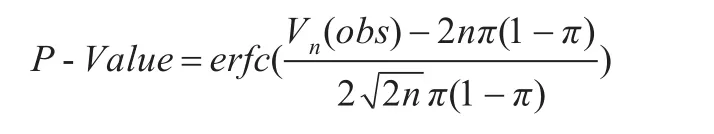
其中，π通过步骤1计算得到，函数erfc()如式（2）所示。

若P-Value的值小于0.01，则认为测试的序列不是随机序列；反之，则认为序列是随机序列。

（3）离散傅里叶变换（谱）测试：离散傅里叶变换（谱）测试的目的是测试序列的周期特性。具体测试方法如下：

步骤1将0，1组成的序列转换成由-1，1组成的序列，设序列的长度为n，转换方式为xi=2εi-1，i=1，2，…，n。其中，εi，xi为转化前后的比特值。

步骤2对转换后的序列X进行离散傅里叶变换（DFΤ），得到序列S=DFT(X)。设Sj为S中第j个元素，则

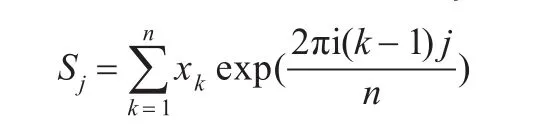
其中，exp(2πik/n)=cos(2πkj/n)+isin(2πkj/n)，j=0，1，…，n-1且

步骤3计算M=mod(S′)，其中S′是由S的前n/2个元素组成的子序列，求模函数mod()用于产生尖峰高度序列。

步骤4计算作为尖峰高度的95%的阀值。

步骤5计算N0=0.95n/2，表示值小于T的尖峰的期望的理论数量。

步骤6计算N1，它表示M中实际观察到的值小于T的尖峰数量。

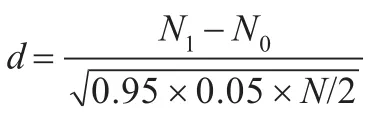
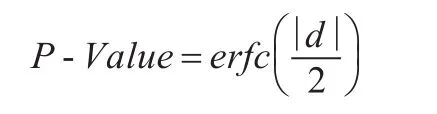
若P-Value的值小于0.01，则认为测试的序列不是随机序列；反之，则认为序列是随机序列。

（4）相关特性：相关特性包括自相关和互相关，由于时空混沌同时产生多个序列，只有它们之间的互相关性满足要求才能同时使用。期望不同格点产生的混沌序列的自相关函数类似于函数δ，而互相关函数的值接近于零。设a(i)，a(j)代表长度为N的两个不同的序列，根据相关性定义，序列a(i)，a(j)的非周期互相关函数为：aˆ(i)为序列a(i)的平均值。当i=j时，即为自相关函数。理想的自相关特性是当m≠0时，C(m)→0，而互相关函数处处为零。在实际中，由于计算精度和序列长度的影响，导致自相关旁瓣和互相关函数不是恒为零，但值很小时（〈0.05），可以认为性能良好。

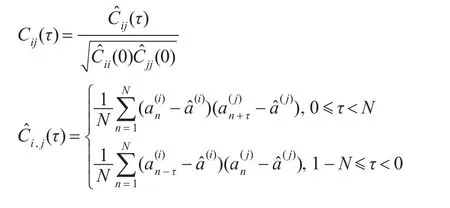
4 符号函数二值化方法及其缺陷

最主要的实值序列二值化方法就是符号函数二值化方法，即

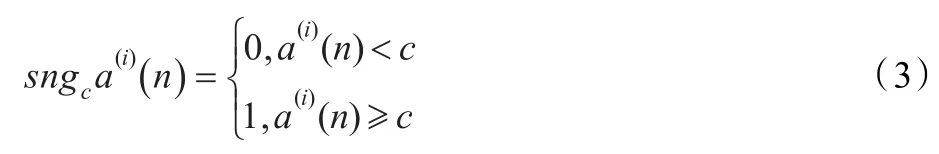
则可由实值混沌序列a(i)(n)产生二进制序列{sngca(i)(n)}。通常取阀值c为序列a(i)(n)的平均值。

本文中用符号sa(i)表示由混沌序列a(i)得到的二值序列。

经过检验可以发现由系统（1）产生的混沌序列经式（3）产生的混沌二值序列的随机性能不好。

从一次实验结果中抽取几个格点的混沌序列，序列长度为10 000，对由式（3）得到的二值序列进行随机性能检验，检验结果如表1所示。

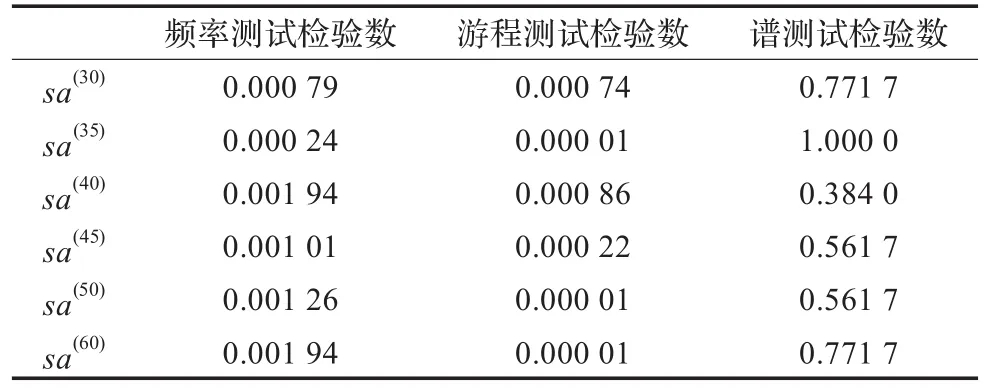
表1 用序列均值做阀值得到的二值序列随机性能检验结果

由表1的数据可以看出，得到的二值序列都没有通过频率测试和游程测试，而谱测试都通过了。

图3是由混沌序列a(30)得到的二值序列sa(30)的自相关图，图4是序列a(30)和a(50)得到的二值序列sa(30)和sa(50)的互自相图，时间间隔取－500～500。由于自相关函数是偶对称的，所以图中只显示单侧的情况。从图中可以看出，序列的自相关性和互相关性的性能是很好的。

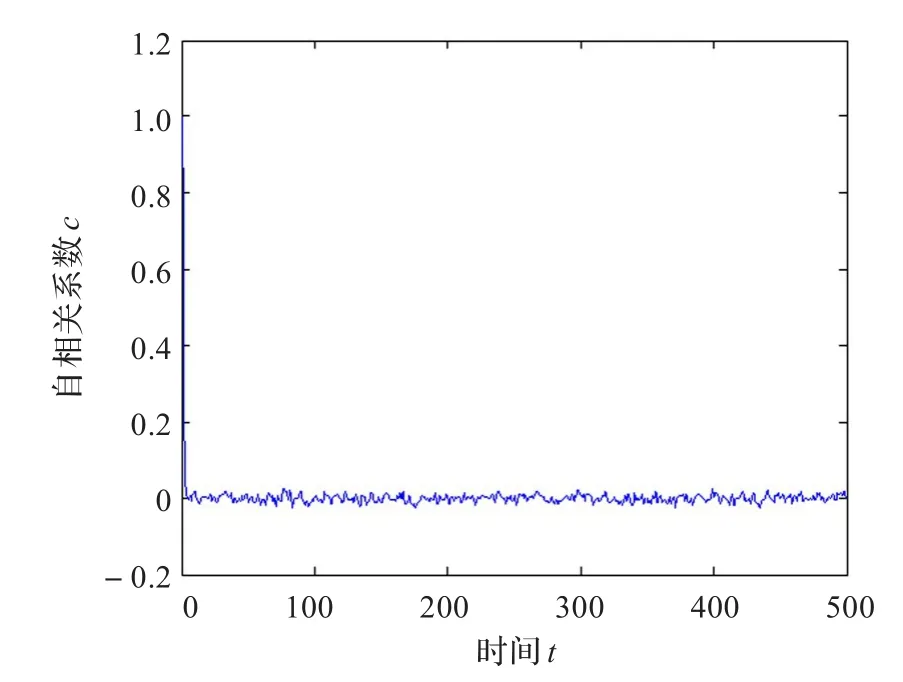
图3 序列sa(30)的自相关函数图

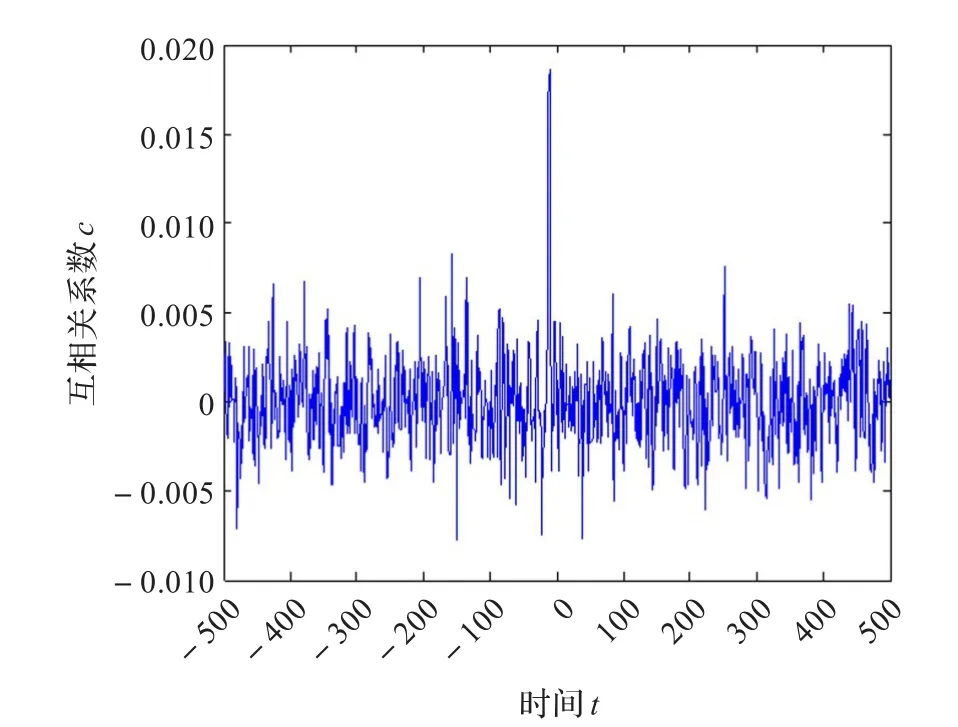
图4 序列sa(30)和sa(50)的互相关函数图

经过大量数值实验发现，由系统（1）产生的混沌序列经式（3）产生的混沌二值序列的随机性能检验多数都不能通过频率测试和游程测试，这说明符号函数二值化法是有缺陷的，而导致这种缺陷的原因应该是方法中阀值的选择没有给出具体的技巧，只有指导性的选择方法。所以本文有针对性地设计了改进的时空混沌二值化方法。

5 改进的时空混沌二值化方法

经过研究发现阀值调整技术和抽取技术可以改善得到的二值序列的性能。

5.1 阀值调整技术研究

观察图2可以发现混沌序列值在均值上下是分布不均的，经过大量研究发现这种分布是相对固定的，所以采用均值做二值化的阀值得到的二值序列的随机性能不好。基于此特点，本文研究了均值附近的不同值做阀值的情况。

以一次实验中第30个格子处得到的混沌序列a(30)为研究对象，序列长度为10 000。图5显示了a(30)在相应阀值时得到的二值序列sa(30)的频率测试的检验数，可以看出阀值c在0.64～0.73之间都可以通过测试，0.69时，检验数取得最大值。图6显示了a(40)在相应阀值时得到的二值序列sa(40)的频率测试的检验数，可以看出阀值c在0.66～0.70之间都可以通过测试，0.68时，检验数取得最大值。

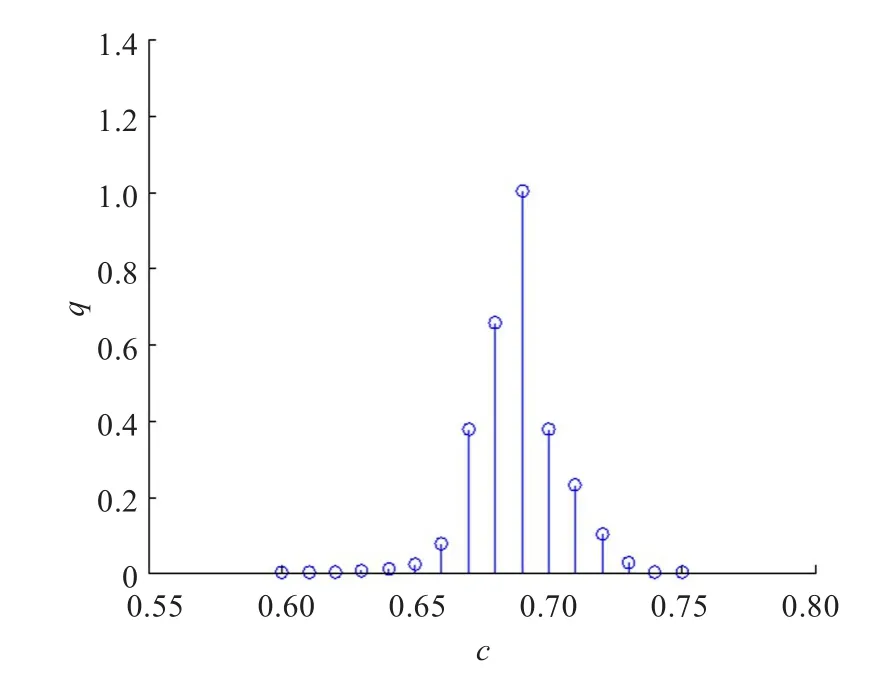
图5 不同阀值时sa(30)的检验数

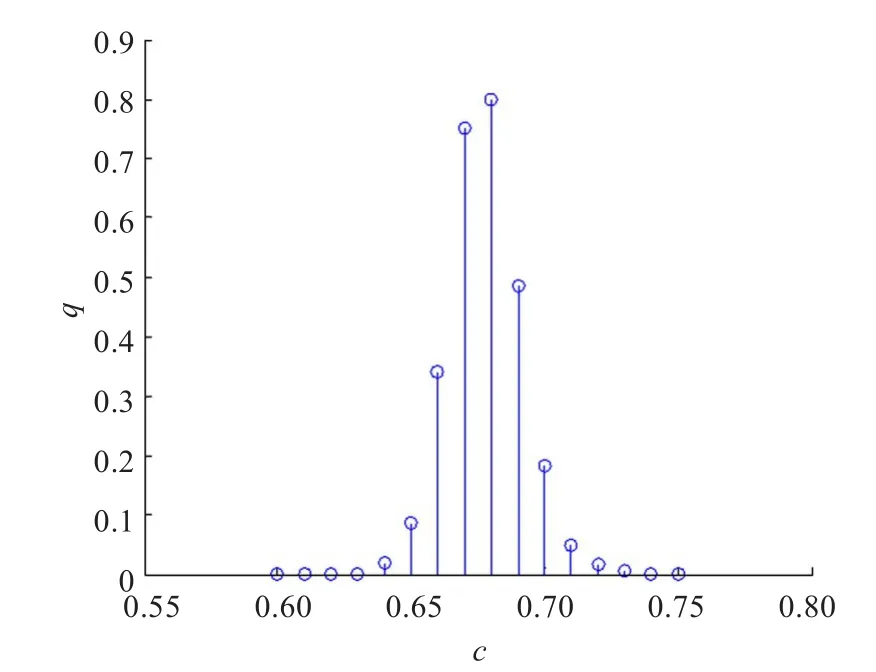
图6 不同阀值时sa(40)的检验数

定义1用符号函数二值化方法时，使得到的二值序列的频率测试检验数最大的阀值称为最优阀值。

经过大量实验研究发现最优阀值总是存在的。任意抽取一次实验产生的混沌序列进行实验，序列长度为10 000。表2列出了相应序列的均值、频率测试通过的阀值区间、最优阀值、采用最优阀值时得到的二值序列的频率测试和游程测试的检验结果。

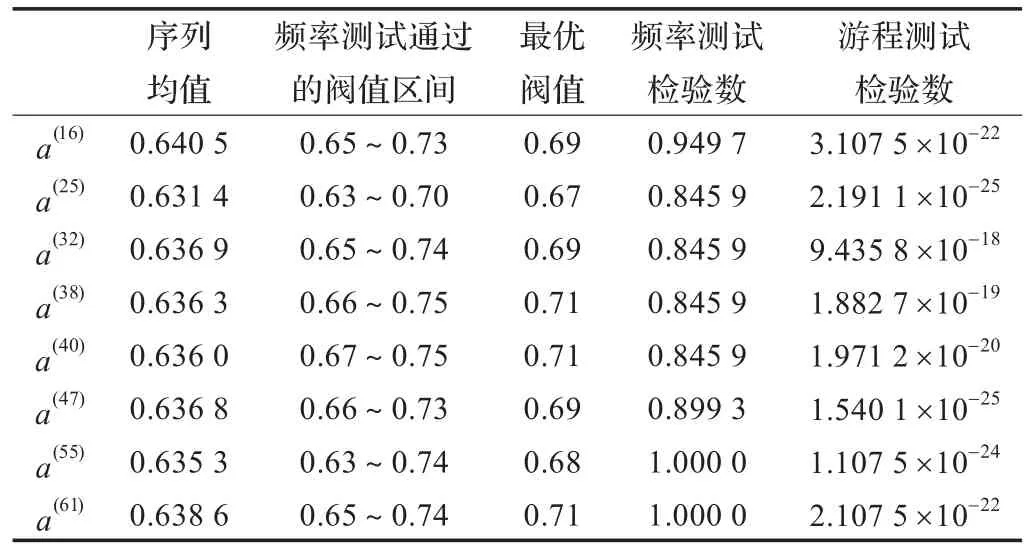
表2 最优阀值得到的二值序列的检验结果

由表2可以看出，通过阀值调整技术可以使得到的二值序列通过频率测试，但游程测试仍然没有通过。实际使用时，可以在平均值附近搜索合适的阀值。但是如果每次使用时都进行最优阀值的搜索，则会降低算法效率，增加计算量，通过大量实验发现，系统（1）产生的混沌序列具有相对固定的均值和最优阀值，最优阀值都在0.69左右。在实际使用时，可以采用固定阀值0.69。

5.2 抽取技术研究

定义2设有序列(xm)=xm(i)，i=1，2，…，N，序列(xn)= xn(i)，xn(i)=xm(3i)，i=1，2，…，p(N/3)，称为序列(xm)的抽取比为1/k的子序列。其中p(·)表示取整运算。

先对混沌序列采用抽取技术再二值化可以提高游程检测的效果，本文计算了对混沌序列抽取比为1/2、1/3、1/4、1/5的子序列采用最优阀值二值化后的二值序列的游程检验的情况，以表2中的序列为例，表3列出不同的抽取比之后的相应的检验数（采用最优阀值）。

由表3可以看出，对混沌序列进行抽取后再用最优阀值二值化后可以通过游程测试，但抽取会减小序列的长度，增大计算量，所以没必要选用过大的抽取比，从表3中可以看出，1/2的抽取就可以。当然，计算量可以接受的情况下，采用1/3的抽取比更好一些。经过大量实验研究发现对由系统（1）产生的混沌序列采用抽取比1/2的抽取后再用最优阀值二值化可以通过游程测试。

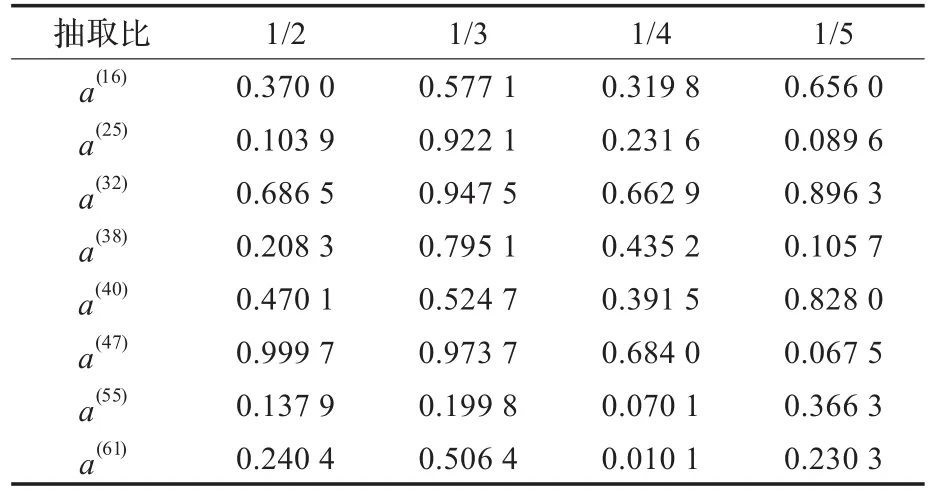
表3 不同抽取比得到的二值序列的游程测试检验结果

5.3 阈值调整技术和序列抽取技术相结合符号函数二值化法

基于以上研究，本文给出阈值调整技术和序列抽取技术相结合符号函数二值化法，具体方法如下：

（2）在得到的序列a(i)k的均值附近进行最优阀值的搜索；

（3）用最优阀值做阀值用式（3）得到二值序列。

从一次实验结果中抽取几个格点的混沌序列，序列长度为10 000，对序列采用阈值调整技术和序列抽取技术相结合符号函数二值化法（取抽取比为1/2，阀值0.69）后得到的二值序列的各项检验结果如表4所示。

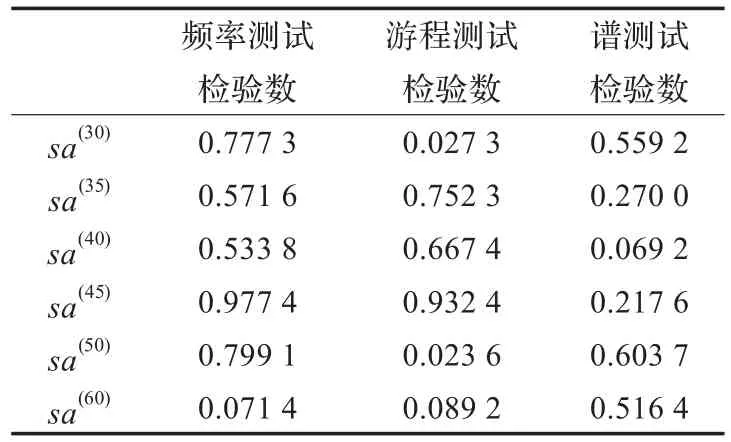
表4 二值序列随机性检验结果（抽取比为1/2，阀值为0.69）

由表4的数据可以看出，得到的二值序列通过了所有测试。

图7是由混沌序列a(30)得到的二值序列sa(30)的自相关图，图8是序列a(30)和a(50)得到的二值序列sa(30)和sa(50)的互相关函数图，时间间隔取－500～500。从图中可以看出，序列的自相关性和互相关性的性能也是很好的。

对系统（1）不同初值产生的50组（每组64个格点）的长度为2万位的混沌序列，由上述方法得到的二值序列进行了随机性能测试，测试结果全部通过了，说明本文提出的方法是有效的。本文还研究了另一种单向耦合映像格子（COML1）：xn+1(i)=(1-ε)f(xn(i))+εf(xn(i-1))

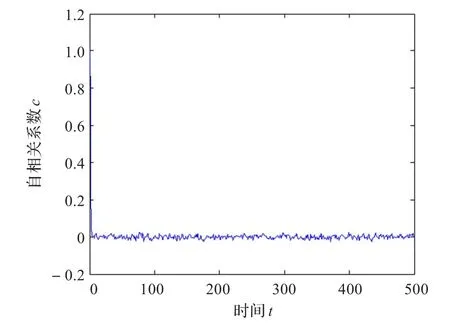
图7 序列sa(30)的自相关函数图

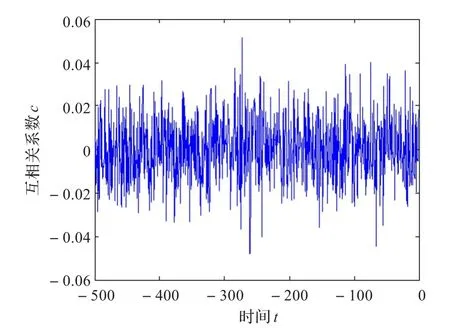
图8 序列sa(30)和sa(50)的互相关函数图

其中f(x)=1-2x2，x∈(-1，1)，n表示离散化后的时间，i表示格子空间坐标。ε为耦合强度，0.75〈ε〈1。

对COML1模型产生的混沌序列也进行了同样的研究，发现COML1模型产生的混沌序列用式（3）生成的二值序列具有同样的特点，不能通过频率测试和游程测试，而采用本文提出的阀值调整技术和抽取技术相结合的改进的符号函数二值化方法后，对随机得到的二值序列进行检验，结果都通过了检验。说明本文提出的方法不仅有效而且有一定的适用性。

6 结论

本文提出的二值化方法，简单实用，按这种方法得到的二值序列具有优良的伪随机性能及相关特性，可以用来作为扩频序列。这种方法既保留了符号函数的运算简单的优点，又增强了方法的适用范围，使得得到的序列满足使用的要求。两种技术可以单独使用，也可结合使用，使用的前后顺序对结果没有影响，而且可以灵活地和其他的二值化方法结合使用。相比起文献[12]中的方法，计算量相当，不需要选择序列，操作简单，并且有望对各种类型的耦合映像格子模型都适用。

[1]高俊山.基于混沌理论的加密过程的研究[J].自动化技术与应用，2001（6）：13-16.

[2]Perez G，Cerdeira H A.Extracting messages masked by chaos[J]. Phys Rev Lett，1995，74（11）：1970-1973.

[3]董斌辉，周健勇，黄金源.混沌伪随机序列生成算法研究[C]//第十一届“保密通信与信息安全现状研讨会”，2009.

[4]程东升，叶瑞松.基于四维混沌系统生成二值序列的方法及其加密应用[J].计算机应用，2008，28（3）：677-679.

[5]姚洪兴，李萌，杜贤利.一种基于超混沌的二值序列生成方法[J].科学技术与工程，2008（13）：3508-3512.

[6]戴跃伟，卓成春，茅耀斌，等.一种二值混沌加密序列的产生及其性能分析[J].南京理工大学学报，2001，25（5）：528-531.

[7]李宁，山秀明，任勇，等.一种实用的时空混沌二值化方法[J].系统工程与电子技术，2002，24（11）：60-63.

[8]彭军，李学明，张伟，等.基于耦合映像格子模型的时空混沌二值序列及其性能分析[J].计算机科学，2005，32（2）：196-198.

[9]陈宇环，易称福，张小红.二维耦合映象格子混沌序列的二值化及特性研究[J].计算机应用与软件，2009，26（7）：222-224.

[10]李红燕，杨万利，罗俊之，等.基于时空混沌系统和脉冲同步控制的加密系统设计[J].装甲兵工程学院学报，2012，26（6）：80-84.

[11]林金秋，司锡才，孟维晓，等.基于混沌的一种图像加密算法[J].计算机应用研究，2010，27（2）：697-698.

[12]赵莉，张雪锋，范九伦.一种改进的混沌序列产生方法[J].计算机工程与应用，2006，42（23）：31-33.

[13]Li P，Li Z，Halang W A，et al.A multiple pseudorandom-bit generator based on a spatiotemporal chaotic map[J].Physics Letters A，2006，349（6）：467-473.

[14]刘金梅，屈强.几类混沌序列的随机性测试[J].计算机工程与应用，2011，47（5）：46-49.

[15]A statistical test suite for random and pseudorandom number generators for cryptographic applications[S].2001.

LI Hongyan,YANG Wanli

Department of Fundamental Courses,Academy of Armored Force Engineering,Beijing 100072,China

According to the characteristic of spatiotemporal chaotic sequences produced by coupled map lattices model,based on the binarization method using sign function,a new binarization method is proposed.Τhe results of randomness and correlation tests show that the randomness of binary sequences given by the new method is good.Moreover these sequences have good correlation.Τhese facts show that the new binarization method proposed in this paper is effective,simple and practive.

spatiotemporal chaos;binarization method;binary sequences;randomness;coupled map lattices

针对耦合映像格子模型产生的时空混沌序列的特点，在符号函数二值化法的基础上，给出了一种新的二值化方法。随机性能和相关性检验的结果表明按这种方法得到的二值序列具有优良的伪随机性能及相关特性，说明提出的方法是有效的，而且简单实用。

时空混沌；二值化方法；二值序列；随机性能；耦合映像格子

A

ΤN914

10.3778/j.issn.1002-8331.1303-0009

LI Hongyan,YANG Wanli.Research on spatiotemporal chaos binarization method.Computer Engineering and Applications,2013,49（21）：65-69.

国家部委预研基金项目资助；装甲兵工程学院创新基金项目资助。

李红燕（1976—），女，讲师，研究领域为混沌控制和保密通信。E-mail：lhyshm1@sina.com

2013-03-04

2013-05-13

1002-8331（2013）21-0065-05

CNKI出版日期：2013-06-18http://www.cnki.net/kcms/detail/11.2127.ΤP.20130618.1601.011.html