一种基于残缺语言判断矩阵的群决策模型
2013-07-20刘卫锋何霞
刘卫锋,何霞
郑州航空工业管理学院 数理系,郑州 450015
一种基于残缺语言判断矩阵的群决策模型
刘卫锋,何霞
郑州航空工业管理学院 数理系,郑州 450015
1 引言
在决策过程中,决策者的偏好信息常常以两两比较的判断矩阵形式给出,其中,由于语言判断矩阵更加能反映出人类思维判断的模糊性、不确定性以及决策问题的复杂性,从而受到决策者的青睐。目前,关于语言判断矩阵的决策问题研究已经成为决策领域研究的一个热点,并取得了丰硕的研究成果。文献[1]利用文献[2]给出的加性语言评估标度定义了加性语言判断矩阵;文献[3]对加性语言判断矩阵进行了研究,给出了一致性加性语言判断矩阵;文献[4]对语言判断矩阵的决策方法进行了系统的研究;文献[5-7]分别研究了不同粒度语言判断矩阵形式偏好信息的群决策问题;文献[8-9]研究了二元语义语言判断矩阵的决策问题;文献[10-11]分别研究了基于语言判断矩阵的群决策方法;文献[12-15]对语言判断矩阵的一致性及其决策问题进行了深入的研究。但是,在进行两两比较过程中,可能会出现决策者对某些比较判断缺少把握,不感兴趣,或者不想发表意见的情况,此时就会导致语言判断矩阵中某些元素的缺失,即会出现残缺语言判断矩阵。目前,关于残缺语言判断矩阵的研究报道并不多见,仍然需要继续研究。文献[3]对残缺加性语言判断矩阵决策方法进行了研究;文献[16]研究了残缺积性语言判断矩阵决策模型;文献[17]提出了残缺语言判断矩阵的一种可能值推断方法;文献[18]提出了一种基于残缺语言判断矩阵的群决策方法;文献[19]研究了基于残缺互反判断矩阵、残缺互补判断矩阵和残缺语言判断矩阵的群决策问题。
在上述研究基础上,本文继续研究专家偏好信息为残缺语言判断矩阵的群决策问题。在创建一个转换公式的基础上,将语言判断矩阵转化为互补判断矩阵,并探讨了判断矩阵转换的一致性,然后,把该转换公式应用到残缺语言判断,将专家个体残缺语言判断矩阵转化为残缺互补判断矩阵;在此基础上,通过和行归一法求出残缺互补判断矩阵的排序向量,并通过建立一个规划模型求出专家群组排序向量公式,从而实现对备选方案的排序择优。最后,通过算例说明了方法的可行性与有效性。
2 相关概念
设X={x1,x2,…,xn}为方案集,专家利用加性语言评估标度[2]S={sα|α=-τ,…,-1,0,1,…,τ}对X中方案进行两两比较,并构造加性语言判断矩阵[1]A=(aij)nn,其中s-τ≤aij≤sτ,aij⊕aji=s0,aii=s0,i,j=1,2,…,n。
定义1[3]设A=(aij)nn是加性语言判断矩阵,若aij= aik⊕akj,i,j,k=1,2,…,n,则称A为一致性加性语言判断矩阵。
定义2[3]设A=(aij)nn是加性语言判断矩阵,若A的部分元素是缺失的,则称A为残缺加性语言判断矩阵,其中缺失元素用x表示,已知的元素满足下列性质:
s-τ≤aij≤sτ,aij⊕aji=s0,aii=s0,i,j=1,2,…,n
为方便起见,令Ω为A中所有已知元素的集合。
定义3[3]设A=(aij)nn是残缺加性语言判断矩阵,若所有已知元素满足aij=aik⊕akj, aij,aik,akj∈Ω,则称A为一致性残缺加性语言判断矩阵。
定义4设A=(aij)nn是加性语言判断矩阵,若满足:(1)当aik≥s0,akj≥s0时,有aij≥s0;(2)当aik≤s0,akj≤s0,有aij≤s0。则称A为满意一致性加性语言判断矩阵。
定义5[2]若矩阵B=(bij)nn满足bij+bji=1,bii=0.5,i,j=1,2,…,n,则称B是互补判断矩阵。
定义6[2]若互补判断矩阵B=(bij)nn满足bij=bik+bkj-0.5,i,j,k=1,2,…,n,则称B是一致性加性互补判断矩阵。
定义7设B=(bij)nn是互补判断矩阵,若满足:(1)当bik≥0.5,bkj≥0.5时,有bij≥0.5;(2)当bik≤0.5,bkj≤0.5时,有bij≤0.5。则称B为满意一致性互补判断矩阵。
定义8[20]设B=(bij)nn是判断矩阵,若其中既含有残缺元素又含有非残缺元素,且非残缺元素满足bij+bji=1,bii=0.5,bij≥0,则称B为残缺互补判断矩阵。
3 决策方法
3.1 转换公式
设X={x1,x2,…,xn}为方案集,E={e1,e2,…,em}为专家群组,专家el根据加性语言标度S={sα|α=-τ,…,-1,0,1,…,τ}对X中方案进行两两比较,构造加性语言判断矩阵
定义9设加性语言标度为S={sα|α=-τ,…,-1,0,1,…,τ},则sα∈S所对应的下标α和α所对应的语言短语可以分别由下面的函数I和I-1得到:

定理2说明,通过定义10中的转换公式,将语言判断矩阵转换为互补判断矩阵之后,决策者事先对任意两个方案优劣关系的判断,并没有发生改变,改变的只是判断的表达形式。因此,该定理保证了本文对偏好信息进行形式上的转换是合理且可行的。


3.2 残缺语言判断矩阵转化为残缺互补判断矩阵
现将定义10中的转换公式推广应用于残缺语言判断矩阵。

3.3 专家群组排序向量确定
假设专家el对方案X提供的残缺互补判断矩阵为,由文献[20]提出的和行归一法可求出Bl的排序向量为同时,令w=(w1,w2,…,wn)为反映出专家群组偏好的排序向量,显然,专家群组排序向量w=(w1,w2,…,wn),应该与每个专家给出的残缺互补判断矩阵Bl的排序向量l=1,2,…,m的离差越小越好。为此,在考虑到专家权重向量λ=(λ1,λ2,…,λm)基础上,可以构造偏差函数:

显然,F(w)越小越好,能够反映出专家群体偏好的排序向量w应使偏差函数F(w)取得最小值。于是,得到如下定理。
定理7设决策方案为X={x1,x2,…,xn},群组专家为E={e1,e2,…,em},专家权重向量为λ=(λ1,λ2,…,λm),专家el对方案X提供的残缺互补判断矩阵为Bl=(blij)nn,由和行归一法可得到Bl的排序向量为l=1,2,…,m,专家群组排序向量为w=(w1,w2,…,wn),则

证明建立下面的规划模型:
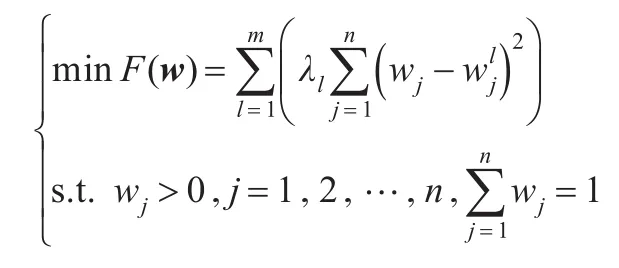
为了求解上述非线性规划模型,构造Lagrange函数:

将上述方程组中的前n个方程相加,并结合第n+1个方程得到α=0,于是得到:

3.4 决策方法及其优越性
在上述研究的基础上,得到将残缺语言判断矩阵转化为残缺互补判断矩阵的一种群决策模型,具体步骤如下:
步骤1利用本文定义11中的转换公式,将专家个体残缺加性语言判断矩阵转化为残缺互补判断矩阵。
步骤2利用文献[20]中的和行归一法求出残缺互补判断矩阵的排序向量。
步骤3利用定理7中公式求出专家群组排序向量。
步骤4由专家群组排序向量对方案进行排序择优。
由本节上述分析论证及决策方法的步骤可以看出,本文决策方法具有以下特点和优越性:
(1)与语言判断矩阵相比,互补判断矩阵的相关理论产生的更早,更为成熟,应用范围也更广,这是本文决策方法产生的最基本的原因,也说明了将语言判断矩阵转换为互补判断矩阵的合理性与优越性。
(2)所建立的转换公式不仅简单而且具有良好的性质,且由定理2可知,通过转换公式将语言判断矩阵转化为互补判断矩阵,改变的只是判断的表达形式,而方案的优劣关系并没有发生改变,这说明了将语言判断矩阵转换为互补判断矩阵的合理性。
(3)本文决策方法只需将残缺语言判断矩阵转化为残缺互补判断矩阵,不需要计算残缺元素,即可利用现成的方法得到残缺互补判断矩阵的排序向量,而文献[3]中需要求出残缺语言判断矩阵中的残缺元素,计算量较大而繁琐。
4 计算实例
例[3]考虑某大学的学院评估问题,一个主要的评估指标为“科研”。设8个学院xi(i=1,2,…,8)将被评估,3位专家e1、e2、e3参与决策,其权重向量λ=(0.5,0.3,0.2),在评估指标“科研”下利用加性语言评估标度:

对方案xi(i=1,2,…,8)进行两两比较,并分别构造了如下残缺加性语言判断矩阵Al(l=1,2,3):

根据3位专家的残缺加性语言判断矩阵,对8个学院的科研情况进行排序择优。
首先,利用转换公式,将残缺加性语言判断矩阵转换为残缺互补判断矩阵:

其次,利用文献[20]中提出的和行归一化方法求出残缺互补判断矩阵B1、B2、B3的排序向量分别为:

于是,由定理7中的计算公式得到专家群组排序向量为:

所以,8个学院的排序为x4≻x2≻x7≻x3≻x6≻x8≻x5≻x1,最佳学院为x4,这与文献[3]中得到的结果是一致的。
5 结束语
研究了专家偏好信息为残缺语言判断矩阵的群决策方法。首先,通过建立一个简单有效的转换公式,将语言判断矩阵转化为互补判断矩阵,同时对判断矩阵的一致性进行了较为系统的研究,并将转换公式推广应用到残缺语言判断矩阵;然后,在利用和行归一法求出残缺互补判断矩阵排序向量的基础上,通过非线性规划模型求出专家群组的排序向量,从而实现备选方案的排序和择优。最后,通过算例说明了方法的可行性和有效性。
[1]Xu Z S.Deviation measures of linguistic preference relations in group decision making[J].International Journal of Management Science,2005,33(3):249-254.
[2]徐泽水.不确定多属性决策方法及应用[M].北京:清华大学出版社,2004.
[3]Xu Z S.Incomplete linguistic preference relations and their fusion[J].Information Fusion,2006,7(3):331-337.
[4]徐泽水.基于语言信息的决策理论与方法[M].北京:科学出版社,2008.
[5]姜艳萍,梁海明.不同粒度语言信息的群体一致性判别和改进方法[J].东北大学学报:自然科学版,2010,31(11):1652-1656.
[6]许永平,王维平,杨峰.基于多粒度多语义语言判断矩阵的群决策方法[J].国防科技大学学报,2010,32(5):173-178.
[7]唐燕武,陈华友,王晓.多粒度语言判断矩阵的一致性研究[J].运筹与管理,2009,18(4):50-53.
[8]巩在武,刘思峰.二元语义判断矩阵的性质及其在航线优选中的应用[J].南京航空航天大学学报,2007,39(4):550-554.
[9]姜艳萍,邢艳楠.二元语义判断矩阵的一致性分析[J].东北大学学报:自然科学版,2007,28(1):129-132.
[10]Han L L,Wei C P.A method for solving multilevel multiobjectivesystembasedonlinguisticjudgmentmatrix[J]. PsychoanalysisandContemporaryScience,2008,21(3):1023-1028.
[11]陈岩,樊治平.基于语言判断矩阵的群决策方法[J].东北大学学报:自然科学版,2004,25(3):303-306.
[12]唐燕武,陈华友.基于相容性的语言判断矩阵的不一致性调整的新方法[J].模糊系统与数学,2010,24(2):112-118.
[13]唐燕武,陈华友.语言判断矩阵的满意一致性判定方法[J].合肥工业大学学报:自然科学版,2010,33(4):621-624.
[14]陈华友,刘金培,陈诚.语言判断矩阵的相容性和一致性研究[J].数学的实践与认识,2008,38(20):173-177.
[15]李彩凤.语言判断矩阵的一致性及排序[J].辽宁工程技术大学学报:自然科学版,2010,29(5):847-849.
[16]Xu Z S.A practical procedure for group decision making under incomplete multiplicative linguistic preference relations[J]. Group Decision and Negotiation,2006,15(6):331-337.
[17]丁叶,朱键军,朱宁宁.残缺语言判断矩阵的可能值推断及决策方法[J].运筹与管理,2010,19(3):75-80.
[18]张尧,樊治平.一种基于残缺语言判断矩阵的群决策方法[J].运筹与管理,2007,16(3):31-35.
[19]Fan Z P,Zhang Y.A goal programming approach to group decision making with three formats of incomplete preference relations[J].Soft Computing,2010,14(10):1083-1090.
[20]徐泽水.残缺互补判断矩阵[J].系统工程理论与实践,2004,24(6):93-97.
LIU Weifeng,HE Xia
Department of Mathematics and Physics,Zhengzhou Institute of Aeronautical Industry Management,Zhengzhou 450015,China
This paper discusses group decision-making problem,which preference information is incomplete linguistic judgment matrices.Firstly,by constructing a transformation formula,additive linguistic judgment matrix is transformed into complementary judgment matrix,and a consistency of transformation of judgment matrices is analyzed.Then,additive incomplete linguistic judgment matrix of each expert is transformed into incomplete complementary judgment matrix by using the transformation formula,and the priority vector of each expert is obtained by using normalizing rank aggregation method for priority of incomplete complementary judgment matrix.Thirdly,according to the priority vector of each expert,the priority vector of expert group is obtained by building and solving a nonlinear programming model,and the priority of alternatives is determined based on the priority vector of expert group.Finally,an example is used to illustrate the feasibility and applicability of the proposed method.
group decision making;incomplete linguistic judgment matrix;incomplete complementary judgment matrix;nonlinear programming model
研究了偏好信息为残缺语言判断矩阵的群决策问题。通过创建一个转换公式,将加性语言判断矩阵转化为互补判断矩阵,探讨了判断矩阵转换的一致性;应用转换公式将专家个体的加性残缺语言判断矩阵转化为残缺互补判断矩阵,并利用残缺互补判断矩阵排序向量的和行归一法,求出专家个体的排序向量;根据专家个体的排序向量,通过建立并求解一个非线性规划模型,得到专家群组的排序向量,从而实现备选方案的排序和择优。通过算例说明了方法的可行性与有效性.
群决策;残缺语言判断矩阵;残缺互补判断矩阵;非线性规划模型
A
O223;C934
10.3778/j.issn.1002-8331.1111-0004
LIU Weifeng,HE Xia.Group decision-making model based on incomplete linguistic judgment matrices.Computer Engineering and Applications,2013,49(13):114-117.
河南省自然科学基金(No.102102310159);河南省哲学社会科学规划项目(No.2011BJJ021);郑州航空工业管理学院青年科研基金(No.2011113003)。
刘卫锋(1976-),男,讲师,主要研究领域为数学建模。E-mail:lwf0519@163.com
2011-11-07
2012-01-14
1002-8331(2013)13-0114-04
CNKI出版日期:2012-04-25http://www.cnki.net/kcms/detail/11.2127.TP.20120425.1723.100.html
