混合择优的多目标免疫粒子群优化算法

仲昭明，李向阳，逄珊

ZHONG Zhaoming1,LI Xiangyang2,PANG Shan3

1.鲁东大学 物理与光电工程学院，山东 烟台 264025 2.烟台联通信息化支撑中心，山东 烟台 264001

3.鲁东大学 信息科学与工程学院，山东 烟台 264025

混合择优的多目标免疫粒子群优化算法

仲昭明1，李向阳2，逄珊3

ZHONG Zhaoming1,LI Xiangyang2,PANG Shan3

1.鲁东大学 物理与光电工程学院，山东 烟台 264025 2.烟台联通信息化支撑中心，山东 烟台 264001

3.鲁东大学 信息科学与工程学院，山东 烟台 264025

1 引言

很多实际工程问题需要同时优化多个目标，这类问题称为多目标优化问题。由于存在多个相互冲突的目标，此类问题不存在单个解满足所有目标，而存在一个折衷解的集合，称为Pareto最优解集或非支配解集[1]。

进化算法是基于种群的智能优化算法，一次运行能够求得问题的多个解，很适合求解多目标优化问题。目前已被成功应用于多目标优化领域，并发展成为一个新的研究方向：进化多目标优化[2-3]。近年来，一些新的智能算法被引入多目标优化问题的求解，其中基于粒子群的多目标优化是近年来逐步发展起来的一个新兴研究方向。同进化算法相比，粒子群算法由于具有控制参数少以及收敛速度快等优点得到迅速发展。

但由于粒子群的单项信息共享机制。算法在多目标优化过程中经常会遇到早熟收敛等问题[4]。并且群中每个粒子都在解集中各自的全局极值的指导下搜索，如果最优解的选取不当，难以获得均布性好的解。因此如何选择粒子的全局极值是十分重要的，对于多目标优化算法解的收敛性和多样性都有很大影响。

为此本文提出一种基于解集信息熵和Sigma值[5]的混合择优机制：种群的粒子以一定概率，根据解集中解的信息熵值或Sigma值选择其全局极值，并且在迭代不同阶段侧重不同的选择原则。该机制充分利用信息熵的密度定义能更好地描述解集分布情况[6]以及Sigma值有助于加速收敛的优点，兼顾了算法的全局和局部搜索能力，有效地改善了解的分布性和收敛性。同时，引入免疫理论中的克隆选择机制直接对解集进行选择搜索，进一步提高了算法的分布性。

2 基于信息熵和Sigma值的混合选择机制

2.1 典型的选择机制分析

粒子全局极值的选取对多目标粒子群优化算法解集的收敛性和分布性都有很大的影响。早期，由Coello[7]等提出的MOPSO借用了PAES[8]等进化多目标优化算法的档案进化策略，将自适应网格法用于解集的维护。把解集划分为网格，根据网格内解的个数设定解的适应度值，网格内解越多其适应度值越小，对所有网格应用轮盘赌方法选择粒子的全局极值。这种方法比较简单，但由于解是随机选择的，因此算法的收敛性有待提高。Raquel[9]等人将NSGA-II中的拥挤距离的概念引入，得到CD-MOPSO。对解集中解的拥挤距离进行排序，据此选择全局极值，其解的分布性较好，但收敛性仍有待提高。此外应用较为广泛的选择机制还包括支配树机制和Sigma机制。支配树机制通过设计支配树的数据结构存储精英解，为粒子选取最优经验，指导粒子飞行。这种机制比Coello的网格机制在解的收敛性上有所提高，但其自身也存在不足：未考虑解的分布情况。Sigma机制则引入参数“σ”来比较粒子和解在空间上的位置关系。如图1所示的二维情况为例，参数σ的定义为：

图1 Sigma机制示意图

通过比较群中粒子和解集中解的σ值，选取二者差值最小的解为全局极值。被选择的全局极值指导粒子沿着直线方向直接逼近Pareto前沿，收敛性较好。但由于Sigma机制未考虑到解的密度信息，在解集中粒子分布不均匀的情况下，容易出现早熟收敛现象，其全局搜索能力有待提高。

为改善算法的性能，一些学者提出将上述机制混合使用，如Junjie[10]等人提出的混合机制，在Sigma机制的基础上综合考虑解的密度信息，在保持算法收敛性的前提下提高了解集的分布性。但该机制中的关于解的密度定义过于简单，有些情况下难以体现解的实际分布情况，并且在每次迭代过程都要进行混合适应度计算，计算量较大。

2.2 混合选择机制

通过对现有选择机制的分析可知：好的选择机制应该能够选择合适的全局极值引导粒子迅速向Pareto前沿飞行，同时还应考虑算法的分布性，尽量选择那些分布比较稀疏的解，使粒子向解空间更广泛的区域进行探索。

为此本文提出一种全局极值的混合选取机制：在每次迭代中粒子依一定概率，根据解集中解的信息熵或者Sigma值选择全局极值。而该选择概率则随着迭代的进行而不断调整：在迭代初期基于信息熵的选择概率较大，选择分布性好的解作为全局极值，以使粒子尽量在解空间全面的探索，提高解集分布性；而在迭代后期则加大基于Sigma值的选择概率，使得种群快速向Pareto前沿逼近，提高解集的收敛性。本文的选择概率如下：

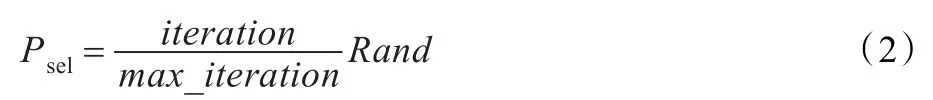
其中，Rand为[0，1]间的随机数，max_iteration为最大迭代次数，iteration为当前迭代次数。

对于种群中的每次迭代，在种群的N个粒子中，随机选择Nσ个粒子按照Sigma机制，从解集中选择Sigma值最为接近的作为全局极值。而剩余粒子则按照信息熵值，利用轮盘赌的方法选择全局极值。其中Nσ按照下式计算：

信息熵的计算：为了保持解集的分布性，许多基于密度或分布的全局极值选择机制被提出，然而这些机制对于解集中解的密度定义过于简单，某个解的密度只取决于直接相邻的解，而没有考虑到更远处解的分布情况。信息熵比传统的拥挤距离等密度定义能更好地描述某个解对于解集分布情况的贡献。因此，为了更准确地反映解集中解的实际分布情况，本文引入信息熵的概念，采用Parzen窗估计法来计算熵值。熵值量化每一个解对Pareto解集分布的贡献。

Pareto解集可表示为Y={yi|i=0，1，…，|Y}，用pyi=P (yi∈Y)表示解集中每个解yi的概率。其熵值为：

其概率计算采用Parzen窗函数计算。Parzen窗估计法是一种具有坚实理论基础和优秀性能的非参数函数估计方法，它能够较好地描述多维数据的分布状态，其基本思想就是利用一定范围内各点密度的平均值对总体密度函数进行估计。Parzen窗定义如下。

解的概率密度估计为：

其中K是核函数，基于正态函数的平滑性将使得估计函数变化平滑，本文采用正态窗核函数：

其中m为目标空间维度，σ是核宽，σ∈Rm。核宽的设置对Parzen窗计算影响较大，这里根据解空间的大小做适应性变化：

其中maxj和minj分别表示解集中第j维的最大、最小值。

计算完解集的信息熵后，粒子用轮盘赌的方法选择其全局极值，信息熵越大，密度分布越好，被选为粒子全局极值的概率就越大。

3 克隆选择机制

为了改善粒子群的搜索能力，文献[11-12]将人工免疫系统中的克隆选择机制应用到标准的粒子群算法当中，其基本思想是：在粒子群进化的每一代，选择最好的若干粒子作为抗体，抗体的适应度函数越大，产生的克隆体越多。这样粒子群算法在纵向完成对整个解空间搜索的同时，克隆选择算子横向地进行局部搜索，提高算法的局部搜索能力。

本文借鉴这种思想，但是根据多目标优化的特点对克隆选择机制进行调整：克隆选择不是应用于种群，而是直接应用于解集，根据解集中解的信息熵而非适应度排序。针对信息熵值最高的前m个解，每个解的生成l个克隆体，然后对所有的克隆体进行变异。算法采用的是与适应度值有关的变异算子[13]。

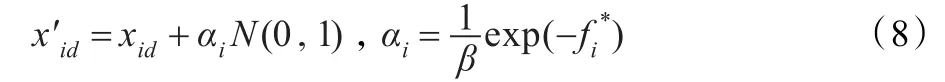
其中N(0，1)是均值为0，标准差为1的Guass随机变量；β是用于控制指数函数衰减的变量，是经过规范化处理的克隆的各维度适应度值。

对每个解和其克隆体进行比较，如果出现支配原解的克隆体，则用克隆体代替原解。这样经过对解集的克隆选择可以获得更为接近Pareto前沿的解集，并且克隆是针对解集中分布较好的若干解直接进行，比对种群进行克隆的效果更为直接。

基于混合择优和克隆选择的多目标粒子群可由以下步骤描述：

（1）初始化粒子群P，确定种群规模为N，初始Pareto解集置空。

（2）计算每个粒子的适应度。

（3）根据Pareto支配关系对解集进行更新，若超出数量限制则进行修剪。

（4）利用混合机制，根据每个粒子的选择概率基于Sigma值或者信息熵值选择全局极值值。

（5）对粒子群中每个粒子的速度和位置进行更新。

（6）更新粒子历史最优值。

（7）Pareto解集进行克隆选择，用支配占优的克隆代替原来的解。

（8）判断是否达到最大迭代次数，若是，结束，输出Pareto最优解集；否则，令iter=iter+1，转（2）。

4 算法验证

4.1 实验设置和性能评价指标

为比较所提出算法（Es-MOPSO）的性能，选择Sigma机制的σ-MOPSO和文献[10]的Nv-MOPSO算法进行对比。为了比较的公平性，三种算法的种群、Pareto解集的规模和迭代次数均相同。其中种群和解集的规模均设置为100，最大迭代次数为200；算法速度更新公式中，惯性权重ω=0.6，c1=c2=2。本文算法指数衰减控制系数β取100，在解集粒子克隆选择个数m取15（即种群粒子数的15%）。

性能仿真实验选取较为常用的测试函数：ZDT1～ZDT4[14]，DTLZ1和DTLZ2[15]。这些测试函数均有已知的Pareto前沿。本文ZDT1～ZDT3测试函数的决策数n取20，ZDT4的n取10。对于DTLZ函数n=k+|xk|-1，本文中取k=3，|xk|=5。

性能评价指标如下所示。

收敛性指标Generational Distance（GD）[16]：

其中n是解集中解的数目，di是每个解距离已知Pareto前沿的最小欧几里得距离。GD值越小说明算法的解集越靠近Pareto前沿。

分布指标SP（Spacing）[17]：

最大展布指标MS（Maximum Spread）[14]（该度量指标用于衡量所得解对Pareto前沿的覆盖程度）：

4.2 实验结果分析

为减少随机因素的影响，三种算法对每个测试函数均独立运行20次。表1和表2分别是三种算法对各测试函数运算结果的收敛性指标、分布指标的平均值和标准差值的比较。

从表1中可以发现，对于收敛性指标GD，本文算法对所有测试函数的结果都明显优于Nv-MOPSO算法。和σ-MOPSO相比，除了测试函数ZDT1和ZDT3是σ-MOPSO取得了最优结果，其余测试函数则是本文算法取得最优结果，但是和σ-MOPSO算法差别不大。从表2中可以发现，对于分布指标SP，本文算法所有的测试函数均得到了最优结果，较另外两种算法有较为明显的提高。对于最大展布指标，如表3所示，除了测试函数ZDT1外，本文算法对于其他测试函数均获得了最优结果，说明混合择优机制有助于发现边界的解，提高解集的最大分布。

表1 三种算法计算得到GD指标平均值和标准差值

表2 三种算法计算得到SP指标平均值和标准差值

表3 三种算法计算得到MS指标平均值和标准差值

图2是三种算法对测试函数DTLZ2独立运行的某次运行结果，其中，图（a）、（b）、（c）分别对应Es-MOPSO、Nv-MOPSO和σ-MOPSO。从图2可以发现，对于三维的测试函数DTLZ2，本文算法由于利用了信息熵表示解的分布情况，得到解集分布明显比其他两种算法的解集更为均匀。

5 算法的参数分析

Es-MOPSO算法的参数有初始种群规模，粒子群的加速系数c1、c2，惯性权重ω，克隆选择机制中指数衰减控制系数β和克隆比例等。其中后两个参数是本文引入的，因此重点针对这两个参数对算法的影响进行分析。

5.1 指数衰减控制系数β的影响

为研究β对算法性能的影响，分别取β为25～150，其他参数设置同前文。图3为对ZDT4函数计算的GD和SP值的变化曲线。如图可见，随着β的增加，GD值减小，收敛性能得到改善，但是SP值增大，分布性变差（对DTLZ1等其他测试函数的验证也可以得到相同的结论，受篇幅限制未列出计算结果）。因此，综合分析两个性能的变化曲线，β值取100左右较为合适。

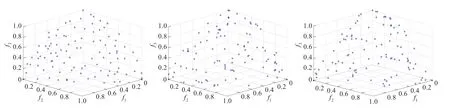
图2 三种算法对DTLZ2函数计算得到Pareto解集分布情况

图3 控制系数对算法收敛性和分布性指标的影响

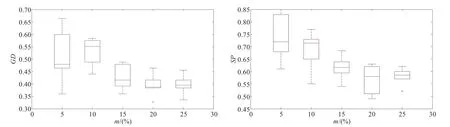
图4 克隆比例对算法收敛性和分布性指标的影响

5.2 克隆比例的影响

为研究克隆比例对算法性能的影响，m分别取5%～25%，其他参数设置同前文，对ZDT4进行计算，计算得到的GD和SP值随m的变化如图4所示。从图中可见，随着m的增加，算法的收敛性和分布性都有所提高（对DTLZ1等其他测试函数的验证也可以得到相同的结论，受篇幅限制未列出计算结果）。当m值达到15%～20%左右时，算法的收敛性能和分布性能较好，如果再提高m，算法性能则没有明显提高且计算量增大，因此m值取15%～20%较为合理。

6 结论

针对多目标粒子群优化算法在解的收敛性和分布性方面的存在的不足，设计了一种全局极值的混合选取机制：按照一定概率，根据解集中解的信息熵或σ值确定粒子的全局极值，选择概率则随迭代进行变化，有效兼顾了解的分布性和收敛性。将免疫算法中克隆选择机制引入算法，直接对解集中信息熵值高的解进行克隆选择，在增强局部搜索性能的同时，进一步提高了解集的分布性。在多个典型测试函数上进行实验，结果证明本文算法在保持较为优越收敛性的同时，显著提高了解集的分布性。对混合择优的多目标免疫粒子群算法进行进一步的理论分析和改进，并用于实际工程问题求解，扩展其应用范围，将是下一步的研究内容。

[1]公茂果，焦李成，杨咚咚，等.进化多目标优化算法研究[J].软件学报，2009，20（2）：271-289.

[2]Deb K.Multi-objective optimization using evolutionary algorithms[M].Chichester：John Wiley&Sons，2001.

[3]Srinivas N，Deb K.Multiobjective optimization using non-dominated sortingingeneticalgorithms[J].EvolutionaryComputation，1994，2（3）：221-248.

[4]Fieldsend J E，Sing S.A multi-objective algorithm based upon particle swarm optimization，an efficient data structure and turbulence[C]//Proceedings of the UK Workshop on Computational Intelligence，Birmingham，2002：37-44.

[5]Mostaghim S，Teich J.Strategies for ending good local guides in Multi-Objective Particle Swarm Optimization（MOPSO）[C]// Proceedings of IEEE Swarm Intelligence Symposium.Indianapolis，USA：IEEE Press，2003：26-33.

[6]Tan K C，Goh C K，Mamun A A，et al.An evolutionary immune system for multi-objective optimization[J].European Journal of Operational Research，2008，187：371-392.

[7]Coello Coello C A，Pulido G T，Lechuga M S.Handling multiple objectives with particle swarm optimization[J].IEEE Transactions on Evolutionary Computation，2004，8（3）：256-279.

[8]Knowles J D，Corner D W.Approximating the non-dominated front using the Pareto archive evolutionary strategy[J].Evolutionary Computation，2000，8（2）：149-172.

[9]Raquel C R，Naval P C.An effective use of crowding distance in multiobjective particle swarm optimization[C]//Proceedings of the Conference on Genetic and Evolutionary Computation. NY：ACM Press，2005：257-264.

[10]Yang J，Zhou J，Liu L，et al.A novel strategy of pareto-optimal solution searching in Multi-Objective Particle Swarm Optimization（MOPSO）[J].Computers and Mathematics with Applications，2009，57：1995-2000.

[11]尚荣华，焦李成，公茂果，等.免疫克隆算法求解动态多目标优化问题[J].软件学报，2007，11（8）：2700-2711.

[12]Gong M G，Jiao L C，Du H F，et al.Multi-objective immune algorithmwithPareto-optimal neighbor-basedselection[J]. Evolutionary Computation，2008，16（2）：225-255.

[13]De Castro L N，Timmis J.Artificial immune systems：a new computational intelligence approach[M].Berlin：Springer-Verlag，2002.

[14]Zitzler E，Deb K，Thiele L.Comparison of multiobjective evolutionary algorithms：empirical results[J].Evolutionary Computation，2000（8）：173-195.

[15]Deb K，Thiele L，Laumanns M，et al.Scalable multi-objective optimization test problems[C]//Proceedings of the IEEE Congress on Evolutionary Computation（CEC 2002）.Piscataway：IEEE Service Center，2002：825-830.

[16]Veldhuizen D A V，Lamont G B.Multi objective evolutionary algorithmresearch：ahistoryandanalysis[R].AirForce Institute，Wright-Patterson AFB，OH，1998.

[17]Schott J R.Fault tolerant design using single and multi criteria genetic algorithm optimization[D].Massachusetts：Cambridge University，1995.

1.School of Physics and Optoelectronic Engineering,Ludong University,Yantai,Shandong 264025,China
2.Informatizatiion Support Center of China Unicom,Yantai,Shandong 264001,China
3.School of Information Science and Engineering,Ludong University,Yantai,Shandong 264025,China

In order to solve the problems of loss in diversity and poor distribution of Pareto solutions in Multi-Objective Particle Swarm Optimization（MOPSO）,a hybrid global best selecting strategy is proposed.Each particle’s global best is selected according to information entropy or Sigma value of solutions with a varying selecting probability.And clone selection strategy is used to update Pareto solution set according to dominance relationships.As a result,the better distributed solutions are exploited. Results on several benchmark functions show that the proposed algorithm has better distribution performance while maintains a good convergence.This indicates that the proposed hybrid strategy is effective in improving the diversity and distribution of MOPSO.

multi-objective optimization;particle swarm optimization;information entropy;clone selection

为解决多目标粒子群优化算法存在解的多样性差、分布不均等问题，提出一种混合择优机制：在迭代过程中每个粒子依概率，根据解集信息熵或Sigma值确定其全局极值；并直接对解集进行基于信息熵的克隆选择，根据支配关系更新解集，充分发掘分布性更好的解。测试函数的仿真实验结果表明，该算法在保持较好的收敛性能的同时，其求解的分布性指标要明显优于其他算法，这说明混合择优机制能够有效地提升多目标粒子群优化算法求解的多样性和分布性。

多目标优化；粒子群；信息熵；克隆选择

A

TP301

10.3778/j.issn.1002-8331.1204-0086

ZHONG Zhaoming,LI Xiangyang,PANG Shan.Multi-objective immune particle swarm optimization algorithm with a hybird global best selecting strategy.Computer Engineering and Applications,2013,49（13）：43-47.

国家自然科学青年基金（No.61102167）；山东省科技发展计划项目（No.2011YD04049）。

仲昭明（1963—），男，副教授，研究方向为智能算法及应用。E-mail：zzm2538@163.com

2012-04-09

2012-06-13

1002-8331（2013）13-0043-05

CNKI出版日期：2012-08-06http://www.cnki.net/kcms/detail/11.2127.TP.20120806.1442.020.html